逻辑优化基础-disjoint support decomposition
先遣兵
在了解 disjoint support decomposition 之前,先学习两个基本的概念。
- disjoint
数学含义上的两个集合交集,所谓非相交,即交集为空集。
A∩B=C=⊘A \cap B = C = \oslash A∩B=C=⊘
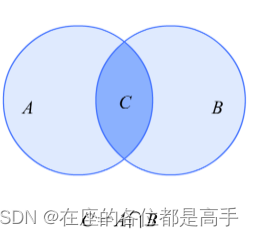
- support
逻辑综合中的 supportsupportsupport 概念是指: 一个门 ggg 的 supportsupportsupport 是指该门 ggg 的所有原始输入PIPIPI。
例如有一个函数:
Fout=h(x)+g(x)Fout = h(x) + g(x) Fout=h(x)+g(x)
其中 h(x)=A+Bh(x) = A + Bh(x)=A+B, g(x)=D+Eg(x) = D + Eg(x)=D+E,则 nodenodenode hhh 和 ggg 的 supportsupportsupport 分别为 { A, B }、{ D, E },FoutFoutFout 的 supportsupportsupport 为 { A, B, D, E }。
其他概念有兴趣可参考 逻辑综合知识点总结 持续更新中…
1. 简介
disjoint support decomposition ,它是用于优化布尔函数的一种技术,将其分解成具有不交 supportsupportsupport 的较小子函数。
一个布尔函数可以表示为 (sum of products,SOP)表达式或积和式(product of sums,POS)表达式。
disjoint support decomposition 的目的是将给定表达式转换为具有较小且更易于处理的子表达式的形式。它的基本思想是识别原始表达式中没有共同变量的变量子集,并将表达式分解为只取决于这些子集的较小表达式的和。这使得函数更容易进行优化,因为较小的表达式通常更容易处理。
即:
非相交分解 == 一个函数 FFF可以被子函数 KKK 和 JJJ 表示,且 KKK 和 JJJ 的 supportsupportsupport 不相交,且 4J$ 只有一个输出,
F=K(x1,x2,...,xj−1,J(xj,...,xn))F = K (x_1, x_2, ..., x_{j-1}, J(x_j, ..., x_n)) F=K(x1,x2,...,xj−1,J(xj,...,xn))
例如有一个函数:
F=(x1+x2)(x3⊕x4)F = (x_1 + x_2)(x_3 \oplus x_4) F=(x1+x2)(x3⊕x4)
最简单的 dsddsddsd 为图 (a) 所示:
K=(x3⊕x4)J1,J1=(x1+x2)K = (x_3 \oplus x_4)J_1, J_1 = (x_1 + x_2) K=(x3⊕x4)J1,J1=(x1+x2)
或者图 (b):
K=(x1+x2)J2,J2=(x3⊕x4)K = (x_1 + x_2)J_2, J_2 = (x_3 \oplus x_4) K=(x1+x2)J2,J2=(x3⊕x4)
再进一步表示为图 © F=K(J1,J2)=(x1+x2)(x3⊕x4)F = K(J_1, J_2) = (x_1 + x_2)(x_3 \oplus x_4)F=K(J1,J2)=(x1+x2)(x3⊕x4)
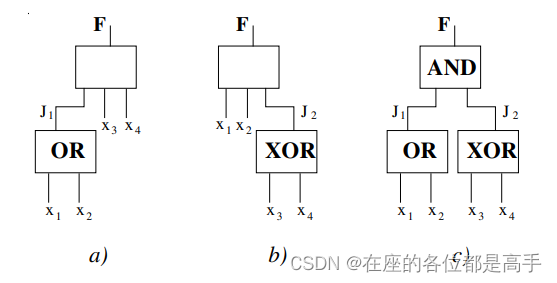
如果一个 outputoutputoutput 被全部用 dsddsddsd 表示,这意味着拿掉某一个 supportsupportsupport 不会对其他的 supportsupportsupport 支持的逻辑造成影响,个人理解是否可以通过 dsddsddsd 分解由局部最优达到全局最优。
如果 FFF被一个 DAG(G)DAG(G)DAG(G) 表示的话,也可以表示为,应该比较容易理解:
Edge(G)=Edge(K)+Edge(J)Edge(G) = Edge(K) + Edge(J) Edge(G)=Edge(K)+Edge(J)
2. 算法
TODO
3. 优点
TODO
相关文章:

逻辑优化基础-disjoint support decomposition
先遣兵 在了解 disjoint support decomposition 之前,先学习两个基本的概念。 disjoint 数学含义上的两个集合交集,所谓非相交,即交集为空集。 A∩BC⊘A \cap B C \oslash A∩BC⊘ support 逻辑综合中的 supportsupportsupport 概念是…...

保姆级使用PyTorch训练与评估自己的DaViT网络教程
文章目录前言0. 环境搭建&快速开始1. 数据集制作1.1 标签文件制作1.2 数据集划分1.3 数据集信息文件制作2. 修改参数文件3. 训练4. 评估5. 其他教程前言 项目地址:https://github.com/Fafa-DL/Awesome-Backbones 操作教程:https://www.bilibili.co…...

Java8新特性:Stream流处理使用总结
一. 概述 Stream流是Java8推出的、批量处理数据集合的新特性,在java.util.stream包下。结合着Java8同期推出的另一项新技术:行为参数化(包括函数式接口、Lambda表达式、方法引用等),Java语言吸收了函数式编程的语法特…...

Java基准测试工具JMH高级使用
去年,我们写过一篇关于JMH的入门使用的文章:Java基准测试工具JMH使用,今天我们再来聊一下关于JMH的高阶使用。主要我们会围绕着以下几点来讲: 对称并发测试非对称并发测试阻塞并发测试Map并发测试 关键词 State 在很多时候我们…...
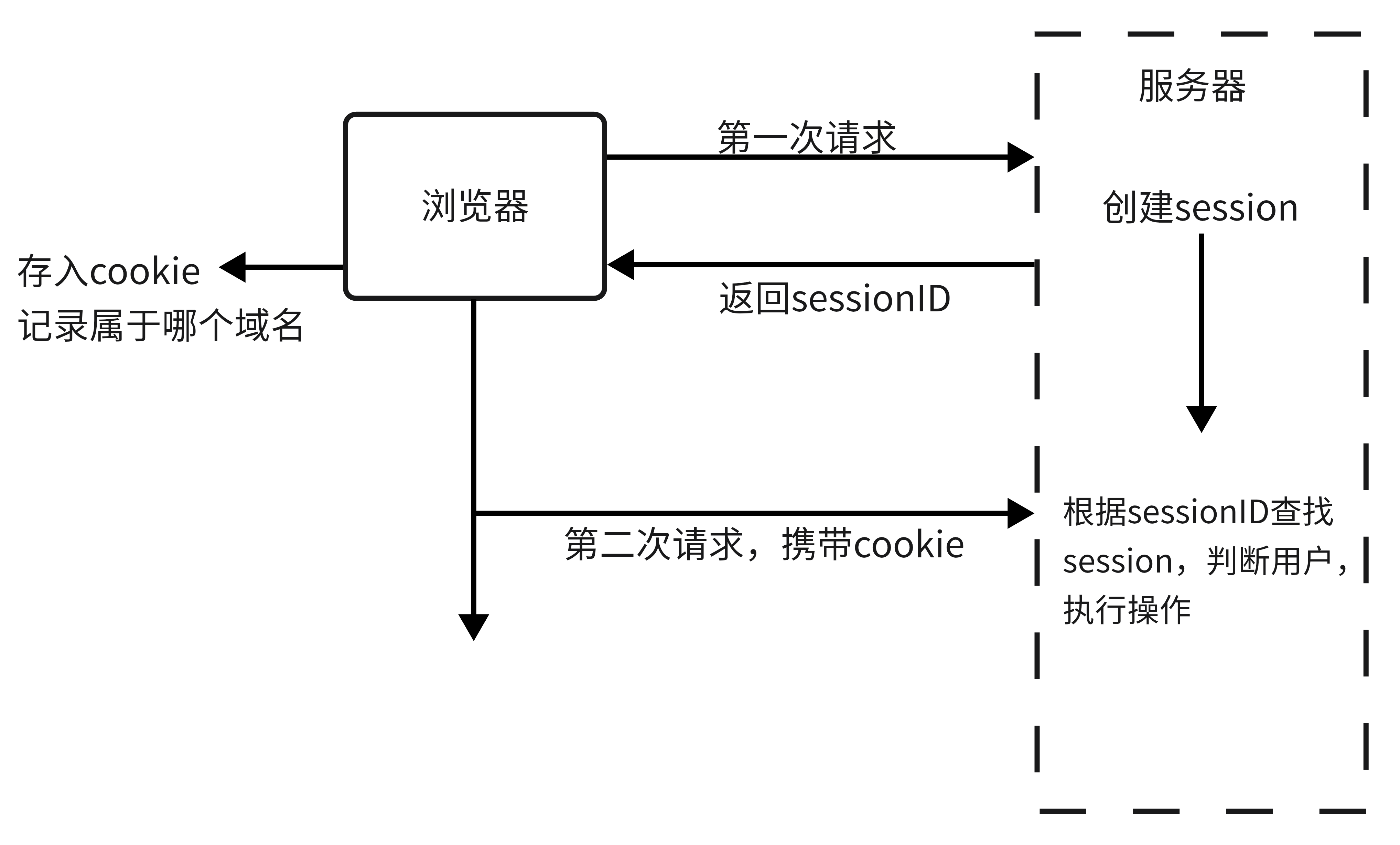
问心 | 再看token、session和cookie
什么是cookie HTTP Cookie(也叫 Web Cookie或浏览器 Cookie)是服务器发送到用户浏览器并保存在本地的一小块数据,它会在浏览器下次向同一服务器再发起请求时被携带并发送到服务器上。 什么是session Session 代表着服务器和客户端一次会话…...

Ubuntu 安装 CUDA and Cudnn
文章目录0 查看 nvidia驱动版本1 下载Cuda2 下载cudnn参考:0 查看 nvidia驱动版本 nvidia-smi1 下载Cuda 安装之前先安装 gcc g gdb 官方:https://developer.nvidia.com/cuda-toolkit-archive,与驱动版本进行对应,我这里是12.0…...
【漏洞复现】Grafana任意文件读取(CVE-2021-43798)
docker环境搭建 #进入环境 cd vulhub/grafana/CVE-2021-43798#启动环境,这个过程可能会有点慢,保持网络通畅 docker-compose up -d#查看环境 docker-compose ps直接访问虚拟机 IP地址:3000 目录遍历原理 目录遍历原理:攻击者可以通过将包含…...

磨金石教育摄影技能干货分享|春之旅拍
春天来一次短暂的旅行,你会选择哪里呢?春天的照片又该如何拍呢?看看下面的照片,或许能给你答案。照片的构图很巧妙,画面被分成两部分,一半湖泊,一半绿色树林。分开这些的是一条斜向的公路&#…...
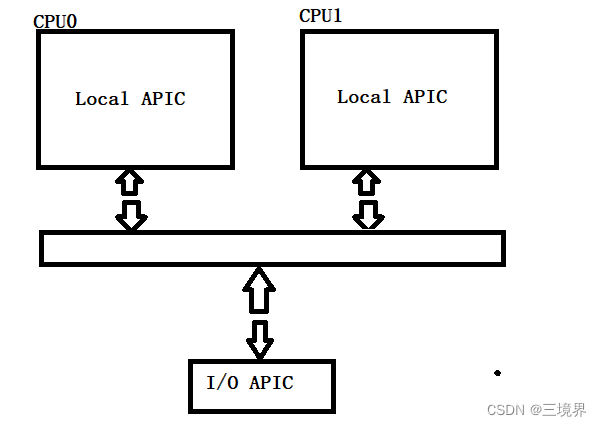
中断以及 PIC可编程中断控制器
1 中断分为同步中断(中断)和异步中断(异常) 1.1 中断和异常的不同 中断由IO设备和定时器产生,用户的一次按键会引起中断。异步。 异常一般由程序错误产生或者由内核必须处理的异常条件产生。同步。缺页异常ÿ…...
SecureCRT 安装并绑定ENSP设备终端
软件下载链接链接:https://pan.baidu.com/s/1WFxmQgaO9bIiUTwBLSR4OA?pwd2023 提取码:2023 CRT安装:软件可以从上面链接进行下载,下载完成后解压如下:首先双击运行scrt-x64.8.5.4 软件,进行安装点击NEXT选…...

ESP32设备驱动-TCS3200颜色传感器驱动
TCS3200颜色传感器驱动 1、TCS3200介绍 TCS3200 和 TCS3210 可编程彩色光频率转换器在单个单片 CMOS 集成电路上结合了可配置的硅光电二极管和电流频率转换器。 输出是方波(50% 占空比),其频率与光强度(辐照度)成正比。 满量程输出频率可以通过两个控制输入引脚按三个预…...
< JavaScript小技巧:Array构造函数妙用 >
文章目录👉 Array构造函数 - 基本概念👉 Array函数技巧用法1. Array.of()2. Array.from()3. Array.reduce()4. (Array | String).includes()5. Array.at()6. Array.flat()7. Array.findIndex()📃 参考文献往期内容 💨今天这篇文章…...
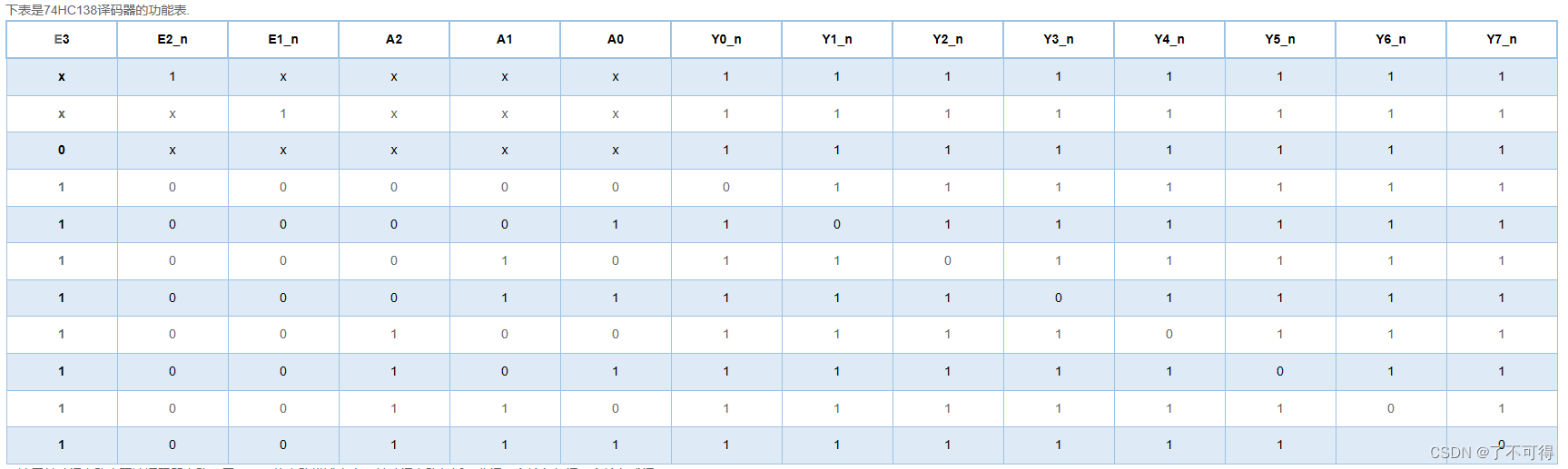
【17】组合逻辑 - VL17/VL19/VL20 用3-8译码器 或 4选1多路选择器 实现逻辑函数
VL17 用3-8译码器实现全减器 【本题我的也是绝境】 因为把握到了题目的本质要求【用3-8译码器】来实现全减器。 其实我对全减器也是不大清楚,但是仿照对全加器的理解,全减器就是低位不够减来自低位的借位 和 本单元位不够减向后面一位索要的借位。如此而已,也没有很难理解…...

2023年全国最新二级建造师精选真题及答案19
百分百题库提供二级建造师考试试题、二建考试预测题、二级建造师考试真题、二建证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 37.下列纠纷中,属于劳动争议范围的有()。 A.因劳动保护发生的纠纷 B.家庭与家政…...
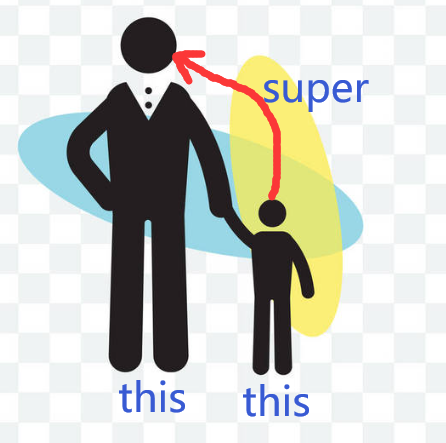
Java中的 this 和 super
1 this 关键字 1.1 this 访问本类属性 this 代表对当前对象的一个引用 所谓当前对象,指的是调用当前类中方法或属性的那个对象this只能在方法内部使用,表示对“调用方法的那个对象”的引用this.属性名,表示本对象自己的属性 当对象的属性和…...

ESP32设备驱动-红外寻迹传感器驱动
红外寻迹传感器驱动 1、红外寻迹传感器介绍 红外寻迹传感器具有一对红外线发射管与接收管,发射管发射出一定频率的红外线,当检测方向遇到障碍物(反射面)时,红外线反射回来被接收管接收,经过比较器电路处理之后,输出接口会输出一个数字信号(低电平或高电平,取决于电路…...

初识BFC
初识BFC 先说如何开启BFC: 1.设置display属性:inline-block,flex,grid 2.设置定位属性:absolute,fixed 3.设置overflow属性:hidden,auto,scroll 4.设置浮动…...

随想录二刷Day17——二叉树
文章目录二叉树9. 二叉树的最大深度10. 二叉树的最小深度11. 完全二叉树的节点个数12. 平衡二叉树二叉树 9. 二叉树的最大深度 104. 二叉树的最大深度 思路1: 递归找左右子树的最大深度,选择最深的 1(即加上当前层)。 class So…...
Weblogic管理控制台未授权远程命令执行漏洞复现(cve-2020-14882/cve-2020-14883)
目录漏洞描述影响版本漏洞复现权限绕过漏洞远程命令执行声明:本文仅供学习参考,其中涉及的一切资源均来源于网络,请勿用于任何非法行为,否则您将自行承担相应后果,本人不承担任何法律及连带责任。 漏洞描述 Weblogic…...
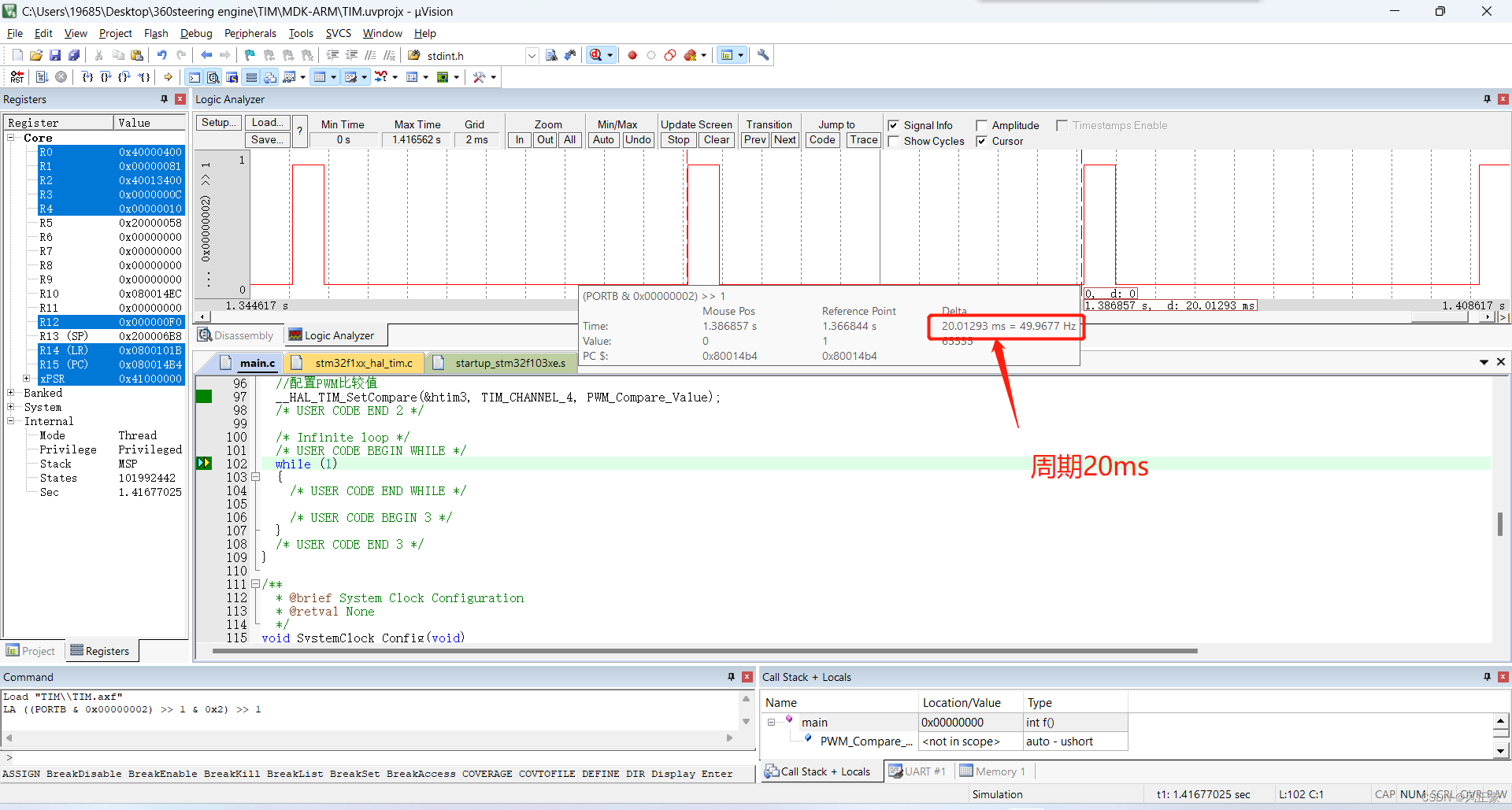
STM32F103CubeMX定时器
前言定时器作为最重要的内容之一,是每一位嵌入式软件工程师必备的能力。STM32F103的定时器是非常强大的。1,他可以用于精准定时,当成延时函数来使用。不过个人不建议这么使用,因为定时器很强大,这么搞太浪费了。如果想…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
