[ROC-RK3399-PC Pro] 手把手教你移植主线Buildroot(基于2023.02-rc3版本)
- 🍇 博主主页:Systemcall小酒屋
- 🍇 博主简介:Neutionwei,C站嵌入式领域新星创作者之一,一枚热爱开源技术、喜欢分享技术心得的极客,注重简约风格,热衷于用简单的案例讲述复杂的技术,“假传万卷书,真传一案例”,这是厦大一位教数学的院士说过的一句话,另外“成就是最好的老师”,技术既要沉淀,也得分享,成就感的正反馈是支持我持续耕耘的动力!
- 🍇 专栏目录:Firefly-RK3399板卡
- 🍇 专栏说明:本专栏主要基于Firefly旗下的RK3399板卡进行入门篇讲述,欢迎订阅,博主会持续更新!

文章目录
- 一、编译环境
- 二、Git环境
- 三、克隆源代码
- 四、编译源代码
- 五、烧录固件
一、编译环境
我的 PC 机用的是 Ubuntu 18.04,执行以下命令安装必要工具:
sudo apt install gcc build-essential bison flex gettext tcl sharutils libncurses-dev zlib1g-dev \
exuberant-ctags g++ texinfo patch vim libtool bc git python3
二、Git环境
配置好自己的邮箱与姓名:
git config --global user.name "userName" //你的用户名
git config --global user.email "email address" //你的邮箱地址
三、克隆源代码
进入官方下载页面,找到克隆仓库:
https://buildroot.org/download.html
克隆源代码:
git clone https://git.buildroot.net/buildroot
使用 git tag 命令可以查看版本情况:
git tag
把页面翻到最底下,可以看到当前最新版本为 2023.02-rc3:
切换到 2023.02-rc3分支:
git checkout -b 2023.02-rc3 2023.02-rc3
四、编译源代码
在主线 Buildroot 中,并没有发现 rk3399 相关的 config 配置文件,但是在历史提交中,我发现被删除掉了。
被删掉的原因是因为编译不过:
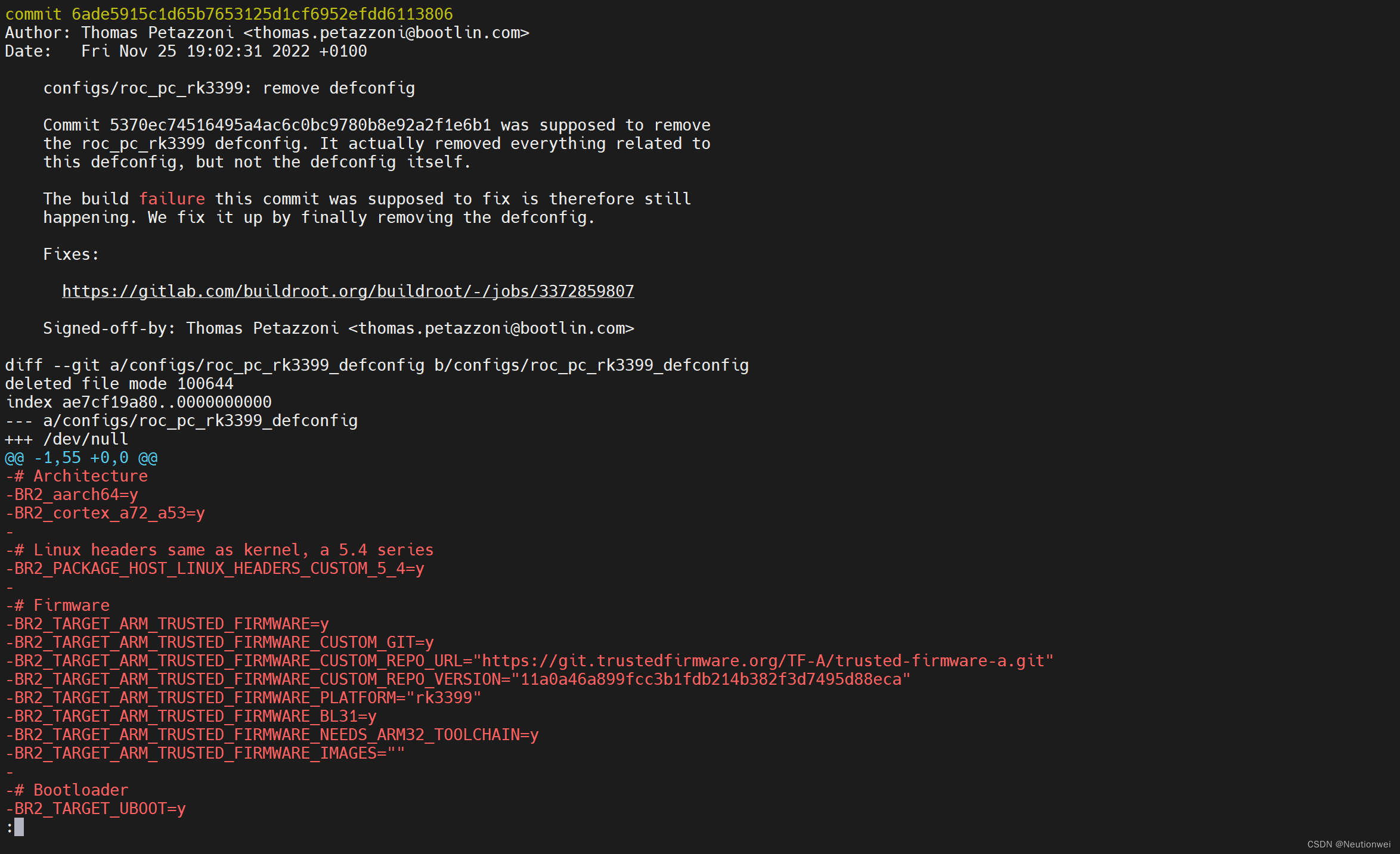
将其 git revert,然后编译:
git revert 6ade5915c1d65b7653125d1cf6952efdd6113806
make roc_pc_rk3399_defconfig
make
第一个编译错误:

打印说一个 arm-trusted-firmware 的源代码编译不过,查看一下原因:
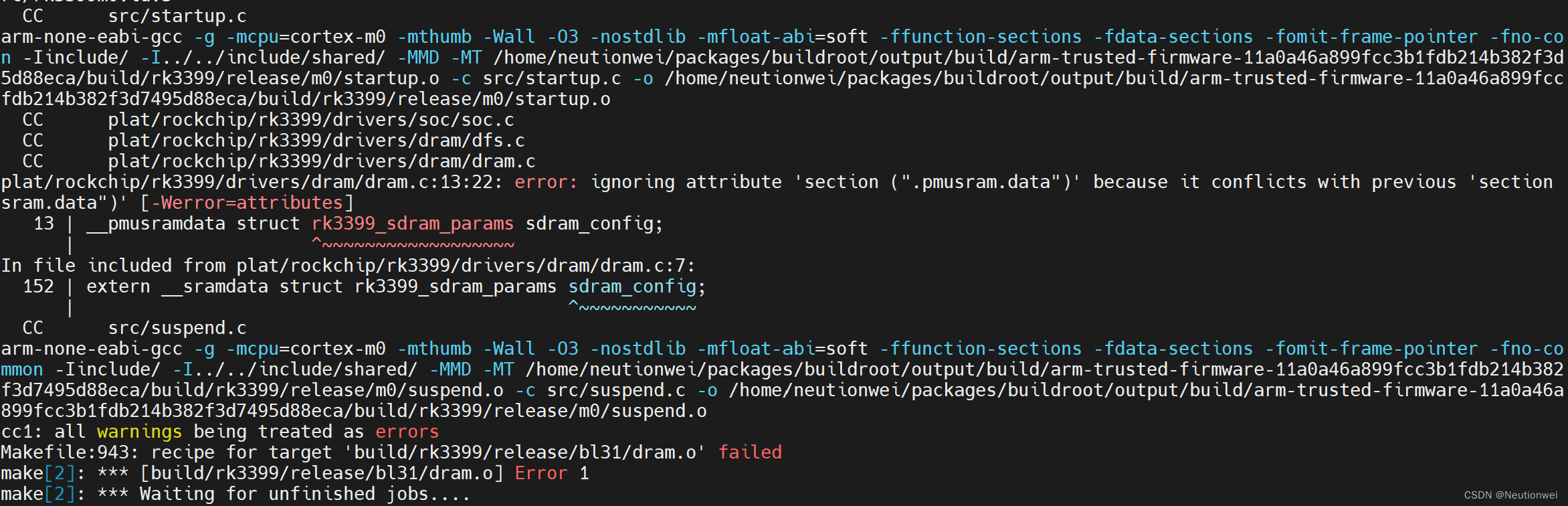
看样子是指定的这个 arm-trusted-firmware 版本存在问题,将其改为主线版本(去掉定制版本):
diff --git a/configs/roc_pc_rk3399_defconfig b/configs/roc_pc_rk3399_defconfig
index ae7cf19a80..3ee8722368 100644
--- a/configs/roc_pc_rk3399_defconfig
+++ b/configs/roc_pc_rk3399_defconfig
@@ -7,9 +7,6 @@ BR2_PACKAGE_HOST_LINUX_HEADERS_CUSTOM_5_4=y# FirmwareBR2_TARGET_ARM_TRUSTED_FIRMWARE=y
-BR2_TARGET_ARM_TRUSTED_FIRMWARE_CUSTOM_GIT=y
-BR2_TARGET_ARM_TRUSTED_FIRMWARE_CUSTOM_REPO_URL="https://git.trustedfirmware.org/TF-A/trusted-firmware-a.git"
-BR2_TARGET_ARM_TRUSTED_FIRMWARE_CUSTOM_REPO_VERSION="11a0a46a899fcc3b1fdb214b382f3d7495d88eca"BR2_TARGET_ARM_TRUSTED_FIRMWARE_PLATFORM="rk3399"BR2_TARGET_ARM_TRUSTED_FIRMWARE_BL31=yBR2_TARGET_ARM_TRUSTED_FIRMWARE_NEEDS_ARM32_TOOLCHAIN=y
重新编译,第二个编译错误如下:
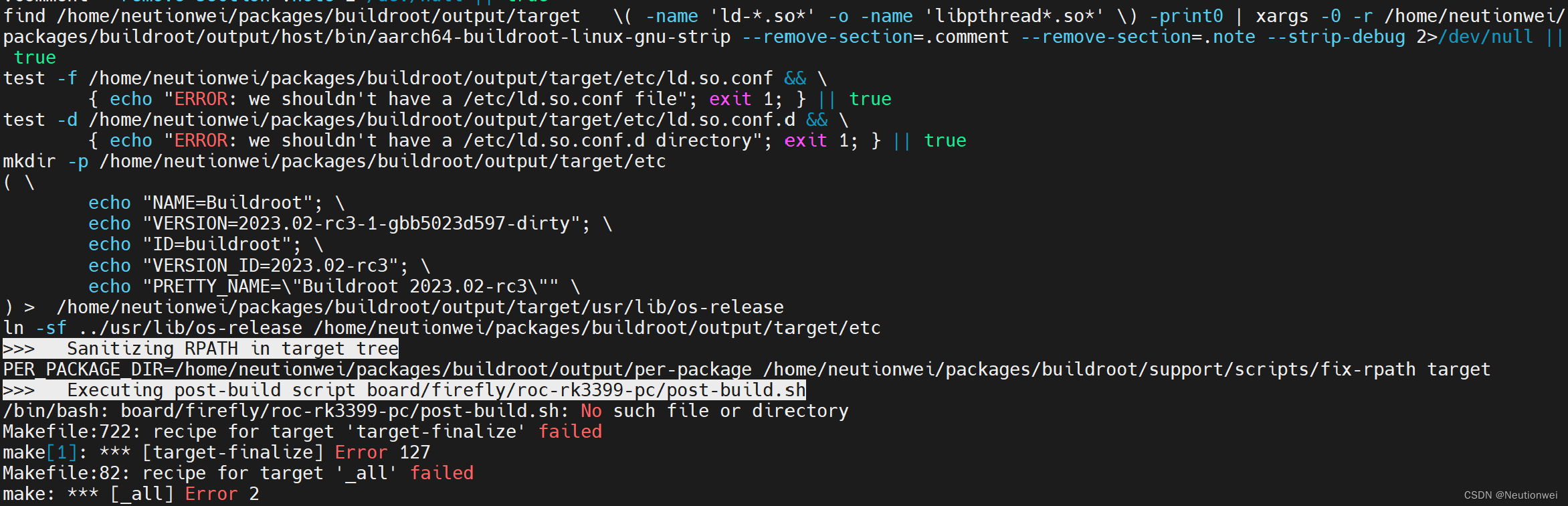
看来是缺少board/firefly/roc-rk3399-pc/post-build.sh这个文件,通过查看历史版本也是被删除掉了:

将其 git revert,然后编译。
一分钟不到编译完成,看来那个脚本是打包使用的:

看样子sdcard.img就是最终打包的 Buildroot 固件。
五、烧录固件
准备一张 TF卡,TF 卡接上读卡器,执行以下命令查看生成的设备节点:
dmesg | tail
我的设备节点是/dev/sdd,把sdcard.img烧录 dd 到 TF 卡:
sudo dd if=sdcard.img of=/dev/sdd conv=notrunc
把 TF 卡接入到 ROC-RK3399-PC Pro TF卡槽,上电启动系统。
如果是使用 Windows 系统,也可以使用 Etcher 工具来烧录:
https://www.balena.io/etcher
最后因为 kernel dts 使用的是早期的 ROC-RK3399-PC(与 ROC-RK3399-PC Pro 存在某些硬件差异),有些驱动可能是不正常。
具体看参考产品规格书:
- ROC-RK3399-PC Pro 产品规格书
- ROC-RK3399-PC 产品规格书
相关文章:

[ROC-RK3399-PC Pro] 手把手教你移植主线Buildroot(基于2023.02-rc3版本)
🍇 博主主页:Systemcall小酒屋🍇 博主简介:Neutionwei,C站嵌入式领域新星创作者之一,一枚热爱开源技术、喜欢分享技术心得的极客,注重简约风格,热衷于用简单的案例讲述复杂的技术&am…...

重温线性代数
前言 对于普通的数学工作者而言,掌握矩阵、线性空间的基本性质和用法比领会抽象的概念更实用。数学专业的同学需要全面深入学习近世代数的理论和演绎法则,例如模的概念和运算。 总之,我个人认为,不论是微积分、还是线性代数&…...

2023河北沃克HEGERLS甘肃金昌重型仓储项目案例|托盘式四向穿梭车智能密集存储系统在工业行业的创新应用
项目名称:自动化仓储托盘式四向穿梭车智能密集立体库项目 项目合作客户:甘肃省金昌市某集团企业 项目施工地域:甘肃省金昌市 设计与承建单位:河北沃克金属制品有限公司(自主品牌:海格里斯HEGERLS&#x…...

软件测试的案例分析 - 闰年5
文章目的 显示不同的博客能获得多少博客质量分 (这是关于博客质量分的测试 https://www.csdn.net/qc) 这个博客得了 83 分。怎么才能得到更多分数? 正文 我们谈了不少测试的名词, 软件是人写的, 测试计划和测试用例也是人写的, 人总会犯错误。错误发生…...

Linux文件基础I/O
文件IO文件的常识基础IO为什么要学习操作系统的文件操作C语言对于函数接口的使用接口函数介绍如何理解文件文件描述符重定向更新给模拟实现的shell增加重定向功能为什么linux下一切皆文件?文件的常识 1.空文件也要在磁盘占据空间 2.文件 内容 属性 3.文件操作 对…...
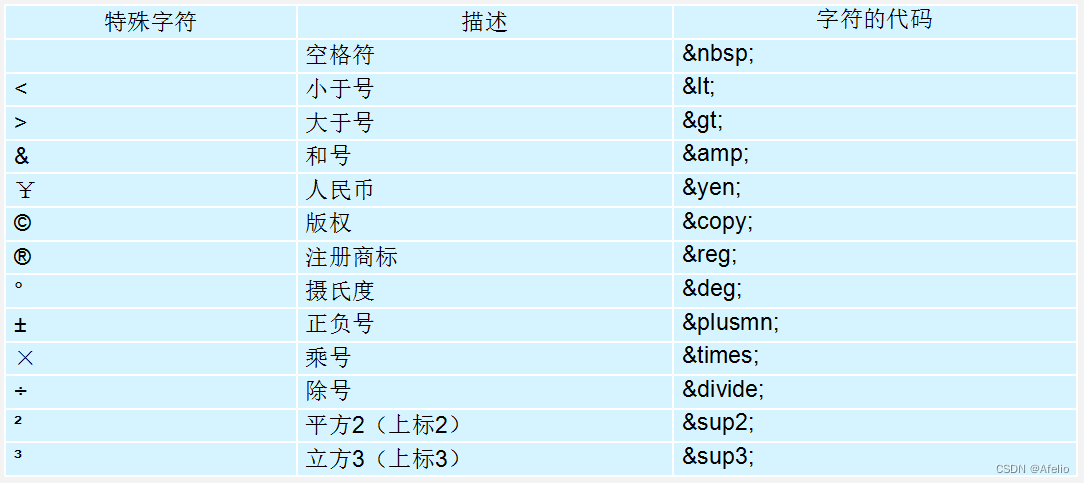
HTML看这一篇就够啦,HTML基础大全,可用于快速回顾知识,面试首选
HTML 1 基础 1.1 DOCTYPE <!DOCTYPE> 文档类型声明,作用就是告诉浏览器使用哪种HTML版本来显示网页。 <!DOCTYPE html> 这句代码的意思是: 当前页面采取的是 HTML5 版本来显示网页. 注意: 声明位于文档中的最前面的位置,处于 标签之前。 …...
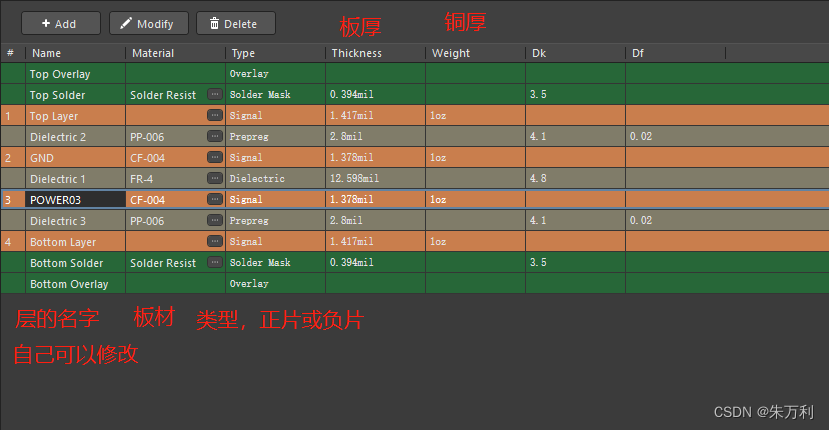
Altium Designer(AD)软件使用记录05-PCB叠层设计
目录Altium Designer(AD)软件使用记录05-PCB叠层设计一、正片层和负片层的介绍1、正片层(Signal)2、负片层(Plane)3、内电层的分割实现二、正片层和负片层的内缩设计1、负片设置内缩20H原则2、正片铺铜设置内缩1、设置规则2、重新铺铜三、AD的层叠设计四、叠层设计需要注意的问…...
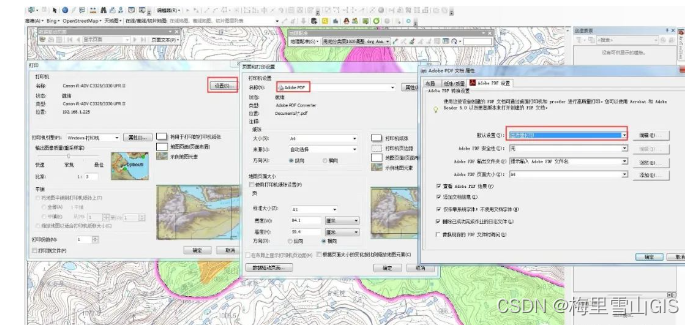
ArcGIS动态表格批量出图
一.产品介绍:ArcGIS动态表格扩展模块Mapping and Charting Solutions,可用于插入动态表格,与数据驱动结合,出图效率无敌。注:优先选择arcgis10.2.2。 二、下载连接: https://www.xsoftnet.com/share/a001CX…...

ChatGPT真神奇,但是也真焦虑
ChatGPT火爆ChatGPT的火爆程度不用说也知道。就目前来说,已经开始冲击各行业了,比如客服、智能助手、语言学习、自然语言处理等等等。。ChatGPT冲击冲击最高的可能就是中间这个段位的了。高段位无法取代,但是低段位,通过使用ChatG…...
mos管驱动与米勒平台介绍、消除
mos驱动设计 1.选择适当的驱动芯片 为了控制MOSFET,需要使用专门的驱动芯片。选择合适的芯片需要考虑MOSFET的电压和电流需求。常见的驱动芯片包括IR2110、IR2184、MIC4424等。 2.设计电路 在驱动电路中,需要加入一些电路元件来保证MOSFET的顺畅工作…...

20230311英语学习
Philosophy of Food: Guidelines for an Authentic Approach to Eating 饮食哲学:值得思考的问题 Whats Philosophical About Food? Philosophy of food finds its basis on the idea that food is a mirror.Eating mirrors the making of a self, that is, the …...
)
【面试题】Nginx面试题汇总(无解答)
什么是Nginx?谈谈个人都理解,项目中是否用到,为什么要用,有什么优点?为什么要用Nginx?为什么Nginx性能这么高?Nginx怎么处理请求的?什么是正向代理和反向代理?使用“反向…...
Java面试总结(六)
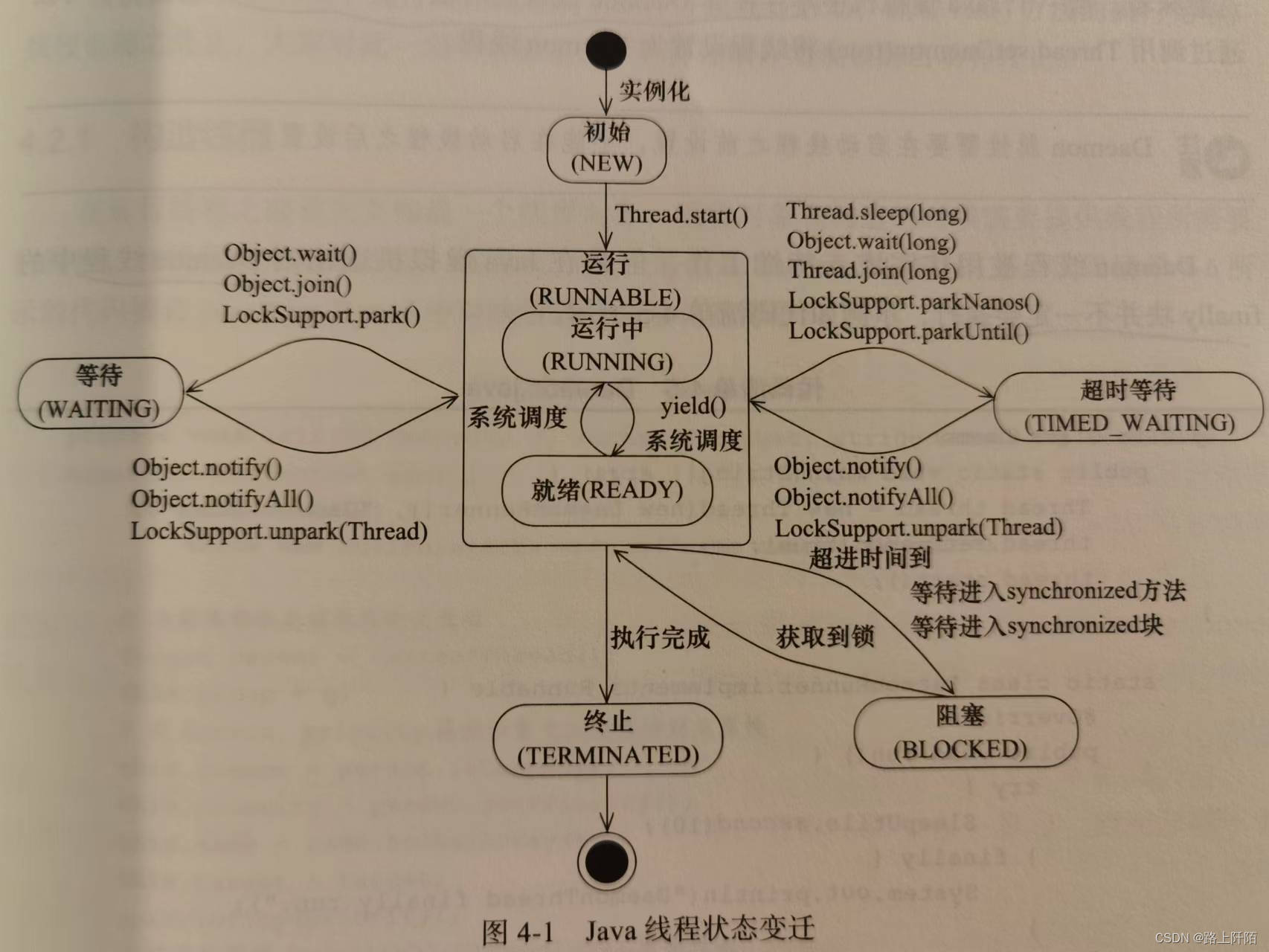
进程和线程的区别 根本区别: 进程时操作系统资源分配的基本单位,而线程是处理器任务调度和执行的基本单位。 资源开销: 每个进程都有自己独立的代码和数据空间(程序上下文),进程之间的切换开销比较大&…...
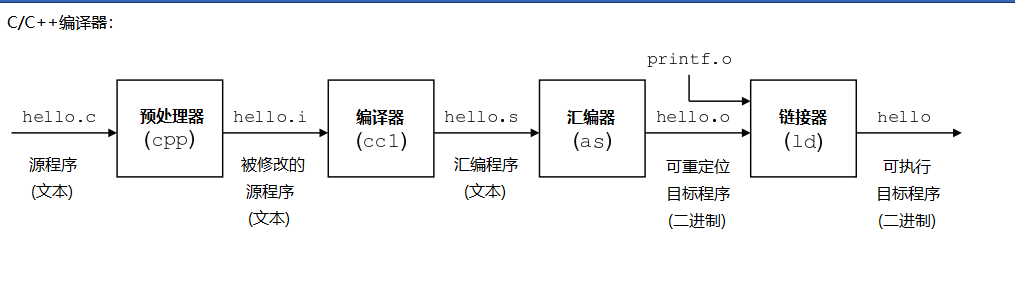
Windows逆向安全(一)C与汇编的关系
前言 逆向是一种新型的思维模式也是软件开发领域中极为重要的技术,涵盖各种维度去深挖软件架构的本质和操作系统原理,学习逆向后可以在各领域中发挥至关重要的作用,其中包括黑灰色,安全开发,客户端安全,物…...

Lazada、Allegro、速卖通测评自养号技术(方法解析)
无论是亚马逊、拼多多Temu、shopee、Lazada、wish、速卖通、煤炉、敦煌、雅虎、eBay、TikTok、Newegg、乐天、美客多、阿里国际、沃尔玛、OZON、Joom、Facebook、Coupang、独立站、Cdiscount、Kaufland、DARTY、Allegro、MANO等平台测评自养号对于卖家来说算是一种低成本、高回…...

Vue3的composition API—setup函数, ref函数,reactive函数
1、Setup 函数 1.setup 是vue3中的一个配置项 2、setup是所有组件所需要的数据和方法都需要配置到setup中的 3、setup两种返回值: 若返回一个对象 若返回一个渲染函数 mian.js文件 注意:尽量不与Vue2混用 setup中无法访问vue2中的配置 不能是async函数…...

国外seo比较好的优化方法有哪些?
随着互联网的不断发展,SEO(搜索引擎优化)变得越来越重要。 对于国外市场,Google搜索引擎是最为重要的搜索引擎之一, 因此在优化国外网站时,需要将Google SEO优化作为首要任务。 关键词研究和优化 在进行…...

【JavaEE进阶】——第一节.Maven国内源配置
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 操作步骤 1.打开项目配置界面(当前项目配置) 2.检查并配置国内源 3.再次打开项目配置界面(新项目配置) 4…...

dockerFile编写
dockerFile编写 语法参数 # DockerFile常用指令 USER # 指定运行的用户,一般不用配置 FROM # 拉取基础镜像,一切从这里开始构建 ARG # 构建参数,只能在dockerFile中使用, # eg: JAR_FILEtarget/springboot-mongo-0.0.1-SNAPSHOT.jar MAI…...
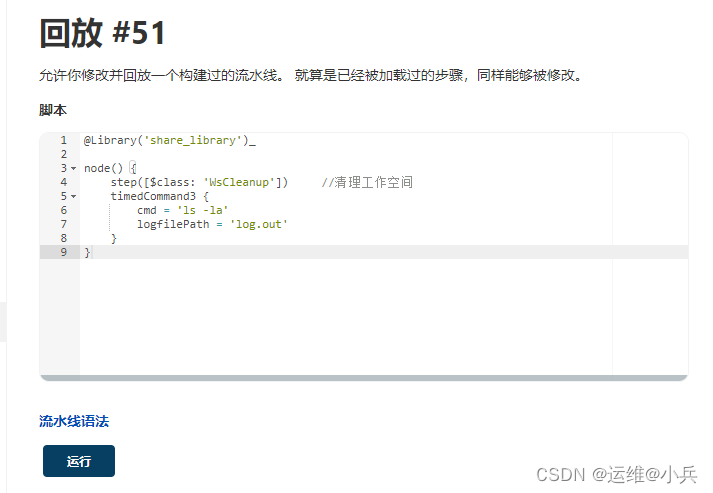
jenkins扩展你的流水线
文章目录一、概述二、可信库和不可信库可信库不可信库三、内部库与外部库内部库SSH访问HTTP 访问外部库配置一个外部库四、在流水线脚本中使用库从源码版本控制中自动下载库加载库到脚本中Library 注解库步骤库指令五、Jenkins 项目中的库范围六、共享库代码的结构src示例一&am…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
