数据分析:置换检验Permutation Test
欢迎大家关注全网生信学习者系列:
- WX公zhong号:生信学习者
- Xiao hong书:生信学习者
- 知hu:生信学习者
- CDSN:生信学习者2
介绍
置换检验是一种非参数统计方法,它不依赖于数据的分布形态,因此特别适用于小样本数据集,尤其是当样本总体分布未知或不符合传统参数检验的假设条件时。置换检验的基本思想是通过随机置换样本来评估观察到的统计量是否显著不同于随机情况下的预期值。最初真正认识置换检验是从PERMANOVA分析开始的,PERMANOVA的原理是:
- 原始统计量的获取: 首先计算组间距离的平方和与组内距离的平方和之间的差值。这个差值在统计学中类似于F分布统计量,用于评估组间差异的显著性。
- 随机置换样本: 接下来,通过随机抽取样本并重新分组,重复计算上述类似F分布的统计量。这个过程需要进行多次,例如1000次,以模拟在随机条件下可能得到的各种统计量值。
- 统计量分布的构建与评估: 将第二步中重复计算得到的1000个统计量值组成一个分布。然后,观察原始统计量值在这个分布中的位置。如果在显著性水平(例如0.05)的两端,即表示原始统计量值在随机情况下出现的概率较低,从而可以认为存在显著差异;如果不是,则不能拒绝原假设,即认为没有显著差异。
置换检验的应用:
置换检验方法通常用于小样本组间的比较,它不对样本的总体分布提出要求。这种方法特别适用于那些样本量较小,以至于无法使用传统的参数检验(如t检验)的情况。然而,如果使用基于简单假设检验的统计量,例如在评估两组数据差异时,首先通过t检验获得原始t统计量,然后通过置换检验重新抽取样本并计算t统计量,最后评估原始t统计量在由置换得到的t统计量分布中的位置,此时就需要考虑数据的分布特性。这种方法允许研究者在不依赖于数据分布的前提下,对统计显著性进行更为稳健的评估。
加载R包
library(tidyverse)
library(multcomp)
library(lmPerm)# rm(list = ls())
options(stringsAsFactors = F)
options(future.globals.maxSize = 1000 * 1024^2)
小样本数据案例
现有两组数据,一组是对照组,一组是实验组,它们的样本量分别是3和5,通过以下数据是否能够证实实验处理可以改善结果?
-
对照组:73,75,78
-
实验组:68,69,80,76,82
解题思路:T检验或Wilcox检验一般要求任意一组样本量均大于等于5较为合适,且两组样本量相差较小(非平衡数据)。该问题样本量较小,普通的假设检验不适合,可以采用置换检验(两组平均值的差值作为统计量)。具体步骤:
- 第一步,零假设是实验组和对照组没有任何差别;
- 第二步,获取原始统计量。先计算两组平均值的差值作为统计量, M 0 = 0.333 M_{0} = 0.333 M0=0.333;
- 第三步,对照组和实验组混合后随机抽取样本组成A和B再计算两组平均值的差值,重复该过程1000次,上述1000次得到的数值组成统计量分布 M 1000 M_{1000} M1000;
- 第四步,计算 M 1000 M_{1000} M1000大于 M 0 = 0.333 M_{0} = 0.333 M0=0.333的个数 n n n,概率 P = n / 1000 P=n/1000 P=n/1000。若 P < 0.05 P < 0.05 P<0.05则说明实验处理有助于提升结果,否则接受零假设。
自己撰写脚本
control <- c(73, 75, 78)
treatment <- c(68, 69, 80, 76, 82)permute_fun <- function(x1, x2, times = 1000) {# x1 = control# x2 = treatment# times = 1000M0 <- mean(x1) - mean(x2)x <- c(x1, x2)M_distri <- c()for (i in 1:times ) {x1_new <- sample(x, length(x1))x2_new <- sample(x, length(x2))M_temp <- mean(x1_new) - mean(x2_new)M_distri <- c(M_distri, M_temp)}dat <- data.frame(Time = 1:times,Value = M_distri)p_value <- length(M_distri[M_distri > M0]) / length(M_distri)p_label <- paste0("Pvalue = ", p_value, " (M1000 > M0)")pl <- ggplot(dat, aes(x = Value)) + geom_histogram(aes(y=..density..), binwidth=.5, color = "black", fill = "white") +geom_density(alpha=.2, fill="#FF6666") +scale_x_continuous(expand = c(0, 0)) +scale_y_continuous(expand = c(0, 0)) +labs(title = "Distribution of M statistics",x = "Mean(group1) - Mean(group2)") +geom_vline(xintercept = M0, color = "red", linetype = "dashed", linewidth = 1) + annotate("text", label = p_label, x = 4, y = 0.14, size = 4) +theme_bw()return(pl)
}permute_fun(x1 = control, x2 = treatment)
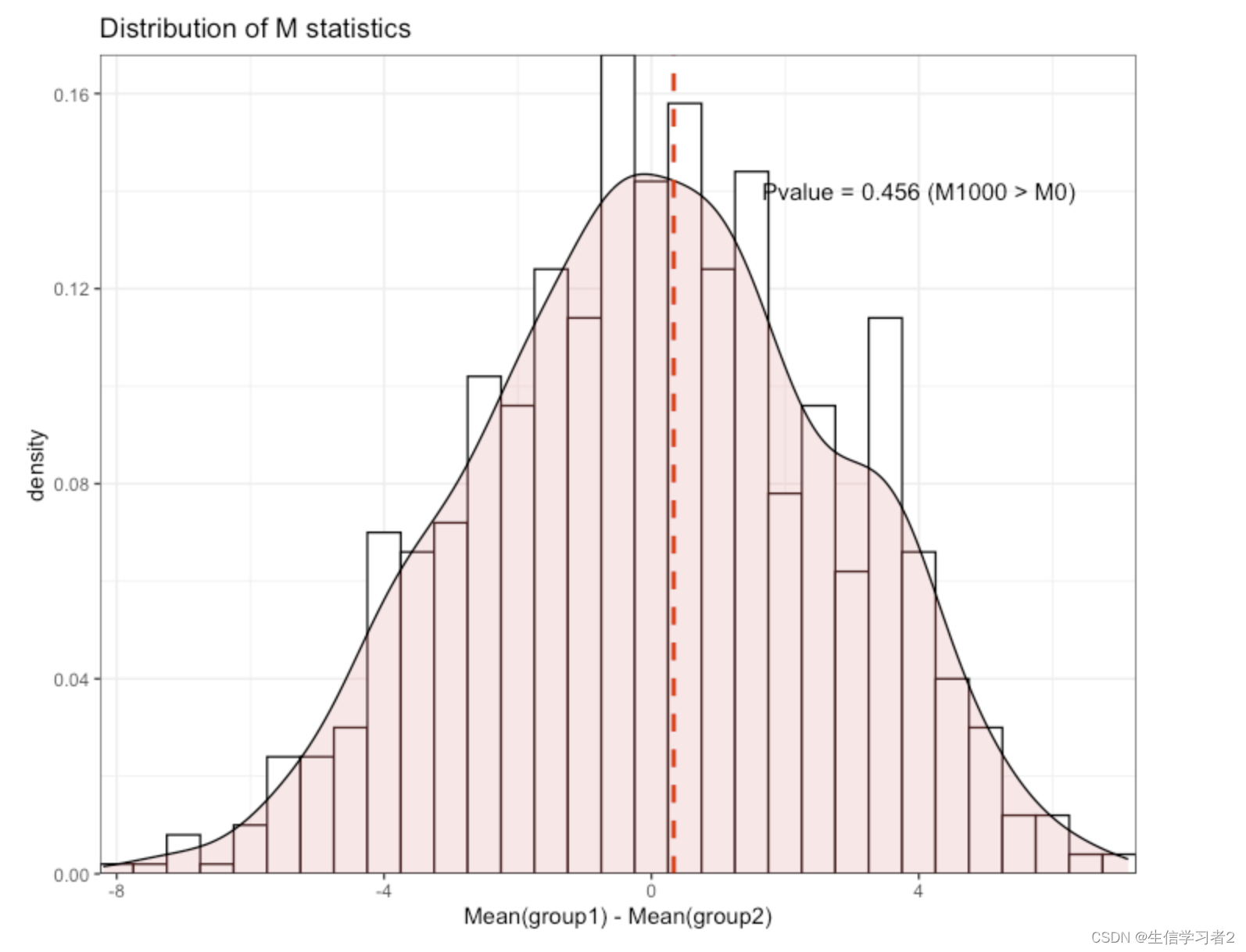
结果:Pvalue > 0.05,说明实验处理对结果没有显著提升。
内置函数
除了自己撰写脚本外,还可以通过R包内置的函数实现两组置换检验。
EnvStats::twoSamplePermutationTestLocation(x = control,y = treatment,fcn = 'mean',alternative = 'greater',mu1.minus.mu2 = 0,paired = FALSE,exact = FALSE,n.permutations = 1000,seed = 123)
Results of Hypothesis Test
--------------------------Null Hypothesis: mu.x-mu.y = 0Alternative Hypothesis: True mu.x-mu.y is greater than 0Test Name: Two-Sample Permutation TestBased on Differences in Means(Based on SamplingPermutation Distribution1000 Times)Estimated Parameter(s): mean of x = 75.33333mean of y = 75.00000Data: x = control y = treatmentSample Sizes: nx = 3ny = 5Test Statistic: mean.x - mean.y = 0.3333333P-value: 0.497
结果:Pvalue > 0.05,说明实验处理对结果没有显著提升。
总结
-
置换检验思想不仅仅可以用于参数未知和分布未知的小样本数据,也可以用于大样本数据(计算代价较高);
-
置换检验也适合组间样本量不平衡的数据。
相关文章:

数据分析:置换检验Permutation Test
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 置换检验是一种非参数统计方法,它不依赖于数据的分布形态,因此特别适…...
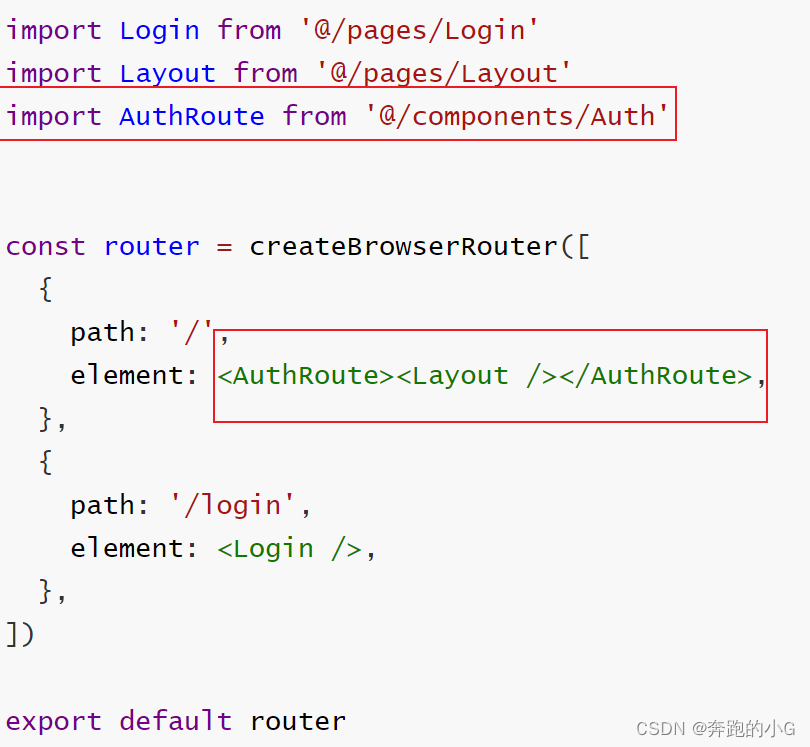
【React】使用Token做路由权限控制
在components/AuthRoute/index.js中 import { getToken } from /utils import { Navigate } from react-router-domconst AuthRoute ({ children }) > {const isToken getToken()if (isToken) {return <>{children}</>} else {return <Navigate to"/…...

机器学习周记(第四十四周:Robformer)2024.6.17~2024.6.23
目录 摘要ABSTRACT1 论文信息1.1 论文标题1.2 论文摘要1.3 论文引言1.4 论文贡献 2 论文模型2.1 问题描述2.2 Robformer2.2.1 Encoder2.2.2 Decoder 2.3 鲁棒序列分解模块2.4 季节性成分调整模块 摘要 本周阅读了一篇利用改进 Transformer 进行长时间序列预测的论文。论文模型…...

JAVA学习笔记DAY10——SpringBoot基础
文章目录 SpringBoot3 介绍SpringBoot 快速入门SpringBootApplication SpringBoot 配置文件统一配置管理Yaml 配置优势tips SpringBoot 整合 SpringMVC静态资源拦截器 interceptor SpringBoot 整合 DruidSpringBoot 整合 MybatisSpringBoot 整合 tx aopSpringBoot 打包 SpringB…...

如何在Android中实现多线程与线程池?
目录 一、Android介绍二、什么是多线程三、什么是线程池四、如何在Android中实现多线程与线程池 一、Android介绍 Android是一种基于Linux内核的开源操作系统,由Google公司领导开发。它最初于2007年发布,旨在为移动设备提供一种统一、可扩展的操作系统。…...

SCI绘图【1】-不同颜色表示密度和差异--密度图
参考资料:密度图(Density Plot) - 数据可视化图表 - 数字孪生百科 密度图是快速观察变量数值分布的有效方法之一。通常情况下,会根据两个变量将平面绘图区域分为非常多的子区域,之后以不同颜色表示落在该区域上样本的…...

C语言 while循环1
在C语言里有3种循环:while循环 do while 循环 for循环 while语句 //while语法结构 while(表达式)循环语句; 比如在屏幕上打印1-10 在while循环中 break用于永久的终止循环 在while循环中,continue的作用是跳过本次循环 …...
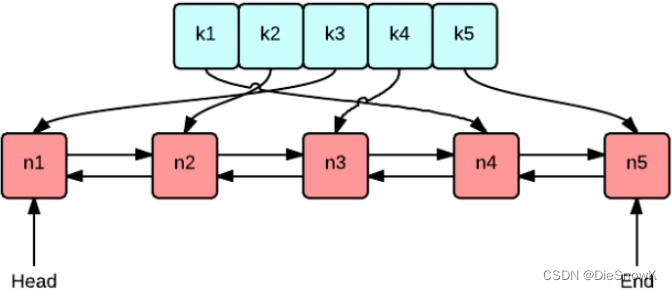
[C++][数据结构][LRU Cache]详细讲解
目录 1.什么是LRU Cache?2.LRU Cache实现 1.什么是LRU Cache? LRU是Least Recently Used的缩写,意思是最近最少使用,它是一种Cache替换算法。什么是 Cache? 狭义的Cache指的是位于CPU和主存间的快速RAM 通常它不像系统…...

怎样激励员工积极应用新版FMEA培训后的知识?
在快节奏的职场环境中,新版FMEA(失效模式与影响分析)的培训无疑是提升员工技能、优化工作流程的重要一环。然而,如何让员工积极地将所学知识应用于实际工作中,却是一个值得深入探讨的问题。下面,深圳天行健…...
)
WDF驱动开发-WDF总线枚举(一)
支持在总线驱动程序中进行 PnP 和电源管理 某些设备永久插入系统,而其他设备可以在系统运行时插入和拔出电源。 总线驱动 必须识别并报告连接到其总线的设备,并且他们必须发现并报告系统中设备的到达和离开情况。 总线驱动程序标识和报告的设备称为总线…...

React useEffect 执行时机
默认情况下,Effect 在每次渲染(包括初始渲染)后运行。 如果 React 的所有依赖项都与上次渲染时的值相同,则将跳过本次 Effect。 useEffect(() > {// 这里的代码会在每次渲染后执行 });useEffect(() > {// 这里的代码只会在…...
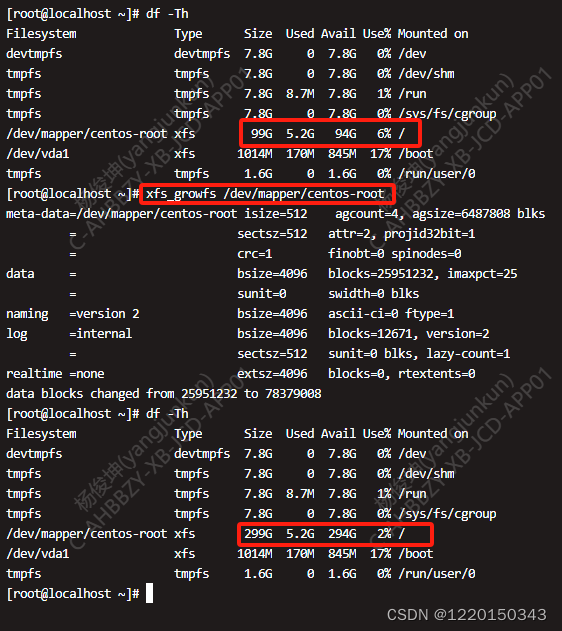
centos7 根目录扩容
1、先检查一下磁盘空间 [rootlocalhost ~]# lsblk 二、使用fdisk创建新分区 [rootlocalhost ~]# fdisk /dev/vdb 1、输入 p ,查看当前分区表; 2、输入 n ,新建一个分区; 3、再输入 p ,选择分区类型为主分区&#x…...

为什么要做Redis分区和分片
Redis分区(Partitioning)和分片(Sharding)是将数据分布在多个Redis实例或多个节点上的做法。这种技术用于提高性能、可扩展性和可用性。以下是执行Redis分区和分片的主要原因: 1. **提高吞吐量**: - 通…...
电脑不小心删除的文件怎么恢复?4个必备恢复方法!
“刚刚在对电脑里的某些垃圾文件进行清理时,我一不小心误删了比较重要的数据。这些误删的数据还有机会恢复吗?希望大家帮帮我,非常感谢!” 在这个数字化飞速发展的时代,电脑早已成为我们日常生活和工作中不可或缺的一部…...
GPTCache:革新大模型缓存,降低成本,提升效率
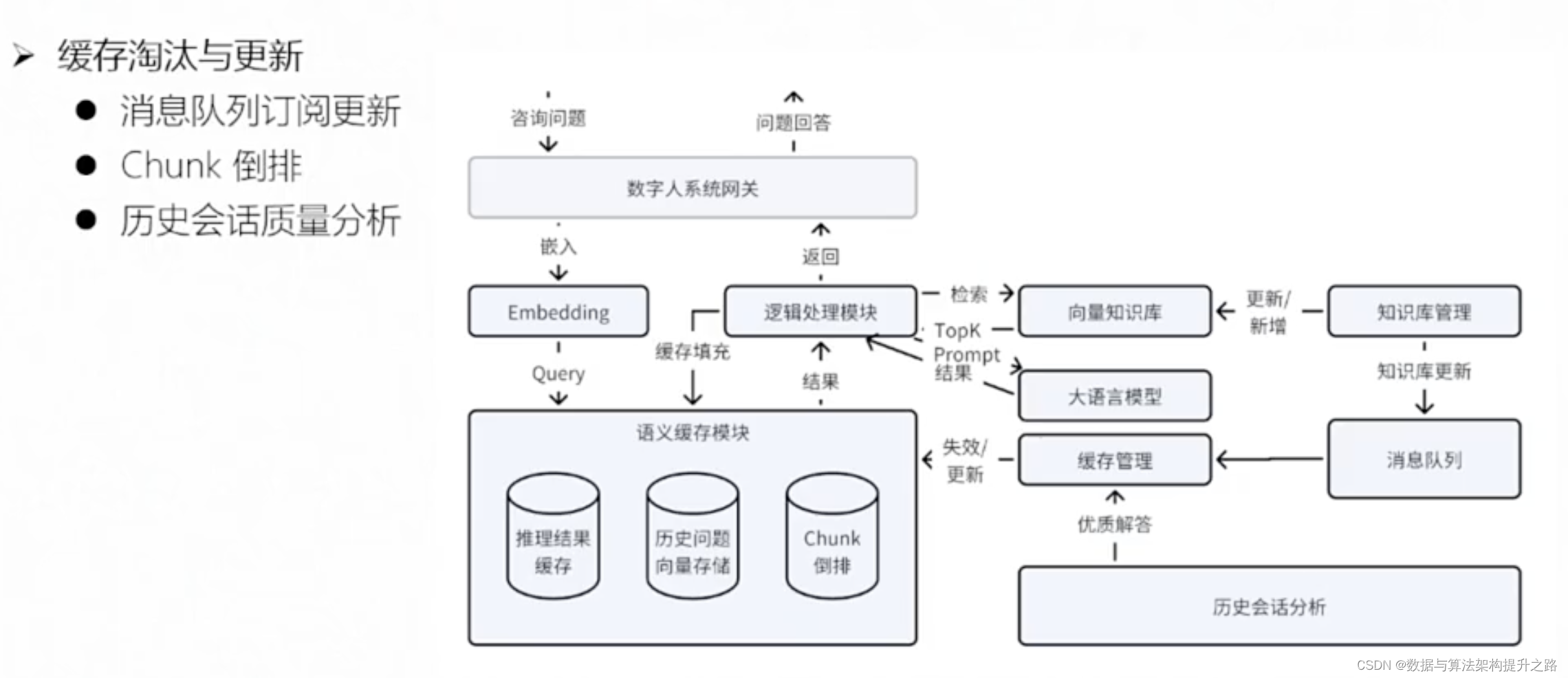
GPTCache介绍 随着应用程序越来越受欢迎并遇到更高的流量水平,与 LLM API 调用相关的费用可能会变得相当可观。此外,LLM 服务的响应时间可能会很慢,尤其是在处理大量请求时。GPTCache是一个致力于构建用于存储 LLM 响应的语义缓存的项目。 项目架构 数字人助力传统客服 1…...

[Day 15] 區塊鏈與人工智能的聯動應用:理論、技術與實踐
區塊鏈的數字身份認證 1. 概述 數字身份認證是當今數字世界中的關鍵問題之一。傳統的身份驗證方法面臨著安全性、隱私性和可信度等方面的挑戰。區塊鏈技術通過其去中心化、不可篡改和可追溯的特性,為解決這些問題提供了新的可能性。本文將深入探討區塊鏈在數字身份…...
绘唐3下载地址
小说推文是一种将小说内容以推文的形式发布的方式,可以吸引更多读者的关注。以下是一些小说推文工具:下载地址 Twitter:Twitter是一个非常受欢迎的社交媒体平台,适合发布小说推文。你可以使用Twitter的140个字符限制来创造悬念和吸…...

两个基因相关性细胞系(CCLE)(升级)
目录 单基因CCLE数据 ①细胞系转录组CCLE数据下载 ②单基因泛癌表达 CCLE两个基因相关性 ①进行数据整理 ②相关性分析 单基因CCLE数据 ①细胞系转录组CCLE数据下载 基因在各个细胞系表达情况_ccle expression 23q4-CSDN博客 rm(list = ls()) library(tidyverse) libra…...

2024全国各地高考录取分数线一览表(含一本、二本、专科)
2024年高考录取分数线陆续公布,上大学网(www.sdaxue.com)为大家整理全国31个省市高考录取分数线汇总,包括本科批、专科批和特殊类招生控制分数线汇总,来看看你的省份多少分能上大学吧。 一、2024年全国高考录取线一览表 1、宁夏 一本线&…...
汇编快速入门
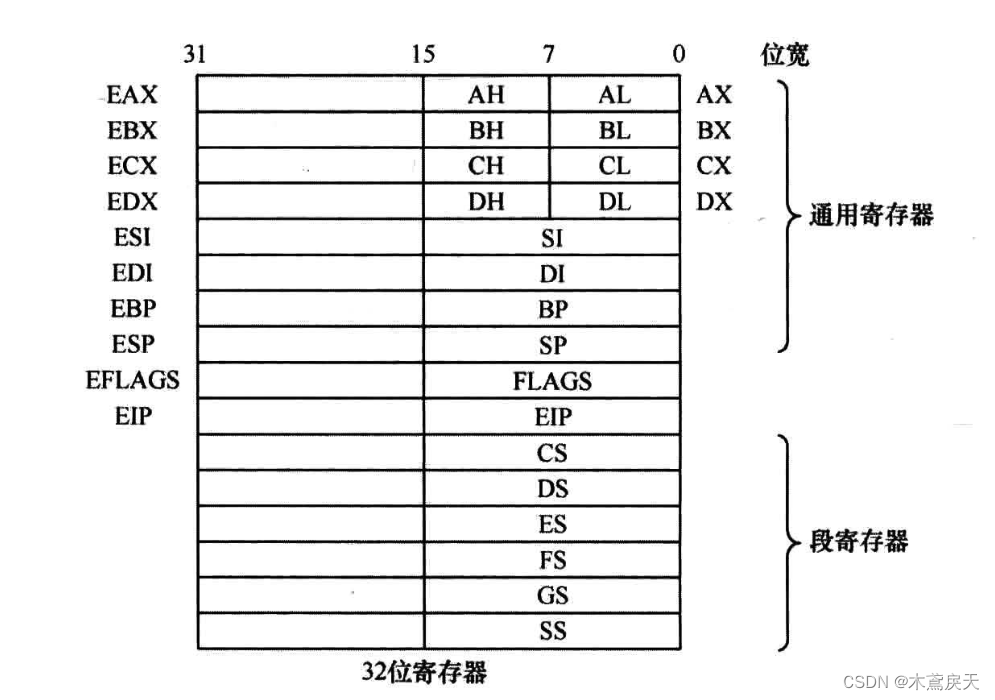
一.基础知识 1.数据类型 DB(Define Byte,字节类型 占位8位bit 1字节) 范围:DB可以用来定义(无符号、有符号)整数(包含二、十、十六进制)和字符 语法:a DB 数据个数…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
