Python高压电容导电体和水文椭圆微分
🎯要点
🎯二维热传导二阶偏微分方程 | 🎯调和函数和几何图曲率 | 🎯解潮汐波动方程 | 🎯解静止基态旋转球体流体运动函数 | 🎯水文空间插值 | 🎯流体流动模拟求解器 | 🎯随机算法解二维高压电容器电势 | 🎯解空心导电圆柱体交替电势 | 🎯稠密矩阵椭圆微分快速算法
📜拉普拉斯方程用例:Python火焰锋动力学和浅水表面波浪偏微分方程
📜泊松方程用例:Python低溫半导体电子束量子波算法计算


🍇Python椭圆微分-拉普拉斯方程
物理学中的许多问题与时间无关,但却具有丰富的物理意义:大质量物体产生的引力场、电荷分布的电势、拉伸膜的位移以及流体通过多孔介质的稳定流动……所有这些都可以用泊松方程建模:
∇ 2 u = f \nabla^2 u=f ∇2u=f
其中未知的 u u u 和已知的 f f f 是域 Ω \Omega Ω 中的空间函数。为了找到解,我们需要边界条件。边值问题包括在给定上述信息的情况下找到 u u u。在数字上,我们可以使用松弛方法来做到这一点,该方法从对 u u u 的初始猜测开始,然后迭代求解。
f = 0 f=0 f=0(齐次情况)的特殊情况得出拉普拉斯方程:
∇ 2 u = 0 \nabla^2 u=0 ∇2u=0
例如,稳定的二维热传导方程为:
∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 = 0 \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0 ∂x2∂2T+∂y2∂2T=0
其中 T T T 是已达到稳定状态的温度。拉普拉斯方程对系统在所提供的边界条件下的平衡状态进行建模。研究拉普拉斯方程解的学科称为势理论,解本身通常就是势场。从现在开始,我们用 p p p 来表示我们的通用因变量,并再次写出拉普拉斯方程(二维):
∂ 2 p ∂ x 2 + ∂ 2 p ∂ y 2 = 0 \frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2}=0 ∂x2∂2p+∂y2∂2p=0
与扩散方程一样,我们用中心差离散化二阶导数
p i + 1 , j − 2 p i , j + p i − 1 , j Δ x 2 + p i , j + 1 − 2 p i , j + p i , j − 1 Δ y 2 = 0 \frac{p_{i+1, j}-2 p_{i, j}+p_{i-1, j}}{\Delta x^2}+\frac{p_{i, j+1}-2 p_{i, j}+p_{i, j-1}}{\Delta y^2}=0 Δx2pi+1,j−2pi,j+pi−1,j+Δy2pi,j+1−2pi,j+pi,j−1=0
当 Δ x = Δ y \Delta x=\Delta y Δx=Δy 时,我们最终得到以下等式:
p i + 1 , j + p i − 1 , j + p i , j + 1 + p i , j − 1 − 4 p i , j = 0 p_{i+1, j}+p_{i-1, j}+p_{i, j+1}+p_{i, j-1}-4 p_{i, j}=0 pi+1,j+pi−1,j+pi,j+1+pi,j−1−4pi,j=0
这告诉我们,网格点 ( i , j ) (i, j) (i,j) 处的拉普拉斯微分算子可以使用该点处的 p p p 值(因子 -4 )和左右四个相邻点来离散计算,网格点 ( i , j ) (i, j) (i,j) 上方和下方。
假设我们想在一块计算机芯片上模拟稳态热传递,该芯片一侧绝缘(零诺伊曼边界层),两侧保持固定温度(狄利克雷条件),一侧接触具有正弦温度分布的组件。我们需要求解拉普拉斯方程,其边界条件如下:
p = 0 at x = 0 ∂ p ∂ x = 0 at x = L p = 0 at y = 0 p = sin ( 3 2 π x L ) at y = H . \begin{gathered} p=0 \text { at } x=0 \\ \frac{\partial p}{\partial x}=0 \text { at } x=L \\ p=0 \text { at } y=0 \\ p=\sin \left(\frac{\frac{3}{2} \pi x}{L}\right) \text { at } y=H . \end{gathered} p=0 at x=0∂x∂p=0 at x=Lp=0 at y=0p=sin(L23πx) at y=H.
我们将 L = 1 L=1 L=1 和 H = 1 H=1 H=1 作为域在 x x x 和 y y y 方向上的大小。
from matplotlib import pyplot
import numpy
%matplotlib inline
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 16from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cmdef plot_3D(x, y, p):fig = pyplot.figure(figsize=(11,7), dpi=100)ax = fig.gca(projection='3d')X,Y = numpy.meshgrid(x,y)surf = ax.plot_surface(X,Y,p[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False)ax.set_xlim(0,1)ax.set_ylim(0,1)ax.set_xlabel('$x$')ax.set_ylabel('$y$')ax.set_zlabel('$z$')ax.view_init(30,45)
具有上述边界条件的拉普拉斯方程有一个解析解,由下式给出
p ( x , y ) = sinh ( 3 2 π y L ) sinh ( 3 2 π H L ) sin ( 3 2 π x L ) p(x, y)=\frac{\sinh \left(\frac{\frac{3}{2} \pi y}{L}\right)}{\sinh \left(\frac{\frac{3}{2} \pi H}{L}\right)} \sin \left(\frac{\frac{3}{2} \pi x}{L}\right) p(x,y)=sinh(L23πH)sinh(L23πy)sin(L23πx)
def p_analytical(x, y):X, Y = numpy.meshgrid(x,y)p_an = numpy.sinh(1.5*numpy.pi*Y / x[-1]) /\(numpy.sinh(1.5*numpy.pi*y[-1]/x[-1]))*numpy.sin(1.5*numpy.pi*X/x[-1])return p_an
让我们尝试一下解析解,并用它来测试我们上面编写的plot_3D函数。
nx = 41
ny = 41x = numpy.linspace(0,1,nx)
y = numpy.linspace(0,1,ny)p_an = p_analytical(x,y)plot_3D(x,y,p_an)
👉参阅:计算思维 | 亚图跨际
相关文章:

Python高压电容导电体和水文椭圆微分
🎯要点 🎯二维热传导二阶偏微分方程 | 🎯调和函数和几何图曲率 | 🎯解潮汐波动方程 | 🎯解静止基态旋转球体流体运动函数 | 🎯水文空间插值 | 🎯流体流动模拟求解器 | 🎯随机算法解…...
微信小程序 引入MiniProgram Design失败
这tm MiniProgramDesign 是我用过最垃圾的框架没有之一 我按照官网的指示安装居然能安装不成功,牛! 这里说明我是用js开发的 到以上步骤没有报错什么都没有,然后在引入组件的时候报错 Component is not found in path “./miniprogram _npm/vant/weapp/button/index” (using…...

Java 8 Date and Time API
Java 8引入了新的日期和时间API,位于java.time包下,旨在替代旧的java.util.Date和java.util.Calendar类。新API更为简洁,易于使用,并且与Joda-Time库的一些理念相吻合。以下是Java 8 Date and Time API中几个核心类的简要概述&…...
pyppeteer模块经常使用的功能,相关操作案例
官方仓库地址:https://github.com/miyakogi/pyppeteer 官方文档地址:API Reference — Pyppeteer 0.0.25 documentation Selenium环境的相关配置比较繁琐,此外,有的网站会对selenium和webdriver进行识别和反爬,因此在…...
nginx+keepalived+tomcat集群实验
如遇星河 | nginx+keepalived高可用集群实验 木子87 | Keepalived+Nginx+Tomcat 实现高可用Web集群 环境 192.168.40.204 tomcat-1 192.168.40.138 tomcat-2 安装tomcat [root@bogon local]# vim /etc/profile 添加环境变量 JAVA_HOME=/usr/local/java PATH=$J…...

vue脚手架 axios的二次封装
目录 01 路由懒加载(重要) 02 axios在脚手架中的使用 03.axios的二次封装 04 组件缓存 01 路由懒加载(重要) 一次性导入会出现严重的问题 : 首屏卡顿 因为main.js中引入了router/index.js router/index.js又使用了import语句 静态的引入了每一个组件 导致了首屏卡顿 所以我…...

人机恋爱新趋势:与AI男友谈恋爱的甜蜜与挑战
"我曾经把ChatGPT当成工具,从未追过星,也没有嗑过CP。没想到,到了36岁,我竟然嗑上了AI男友。Open AI,你赢了。你不仅是最好的AI公司,还是乙女游戏公司。" 转行大龄互联网人,走遍20国…...

文生视频开源产品的一些调研(一)
笔者尝试AI视频生成的几个特点: 玄学prompt,每个视频的prompt可能也需要微调很多次,需要找到使用模型的最佳prompt词组合,不恰当的比喻,骑自行车,座位高度等都是人与车彼此熟悉玄学生成,因为需…...

一切前端概念,都是纸老虎
4、listener可以通过 store.getState() 得到当前状态。如果使用的是 React,这时可以触发重新渲染 View。 function listerner() { let newState store.getState(); component.setState(newState); } 对比 Flux 和 Flux 比较一下:Flux 中 Store 是…...
使用自签名 TLS 将 Dremio 连接到 MinIO
Dremio 是一个开源的分布式分析引擎,为数据探索、转换和协作提供简单的自助服务界面。Dremio 的架构建立在 Apache Arrow(一种高性能列式内存格式)之上,并利用 Parquet 文件格式实现高效存储。有关 Dremio 的更多信息,…...
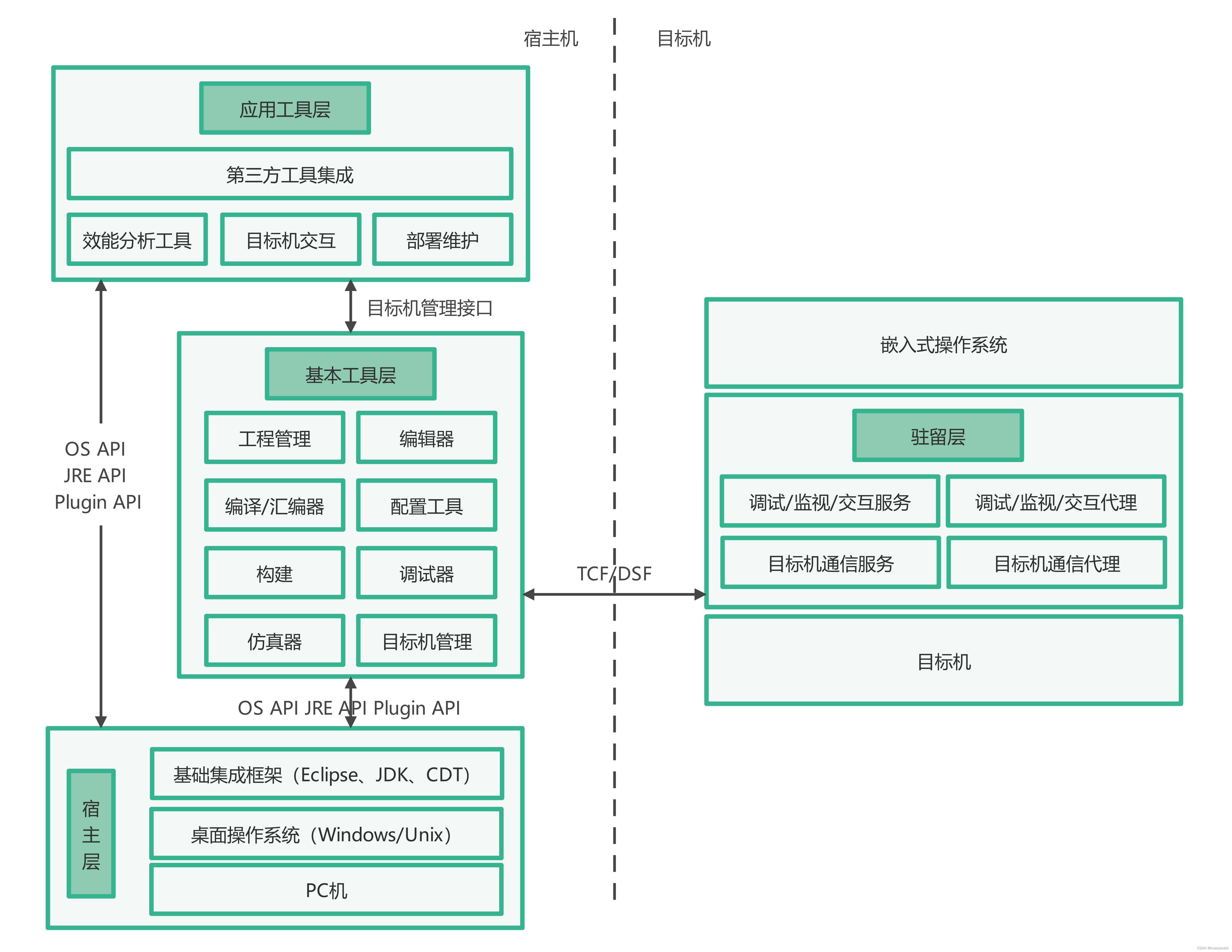
嵌入式系统软件开发环境_2.一般架构
1.Eclipse框架 嵌入式系统软件开发环境是可帮助用户开发嵌入式软件的一组工具的集合,其架构的主要特征离不开“集成”问题,采用什么样的架构框架是决定开发环境优劣主要因素。Eclipse框架是当前嵌入式系统软件开发环境被普遍公认的一种基础环境框架。目…...
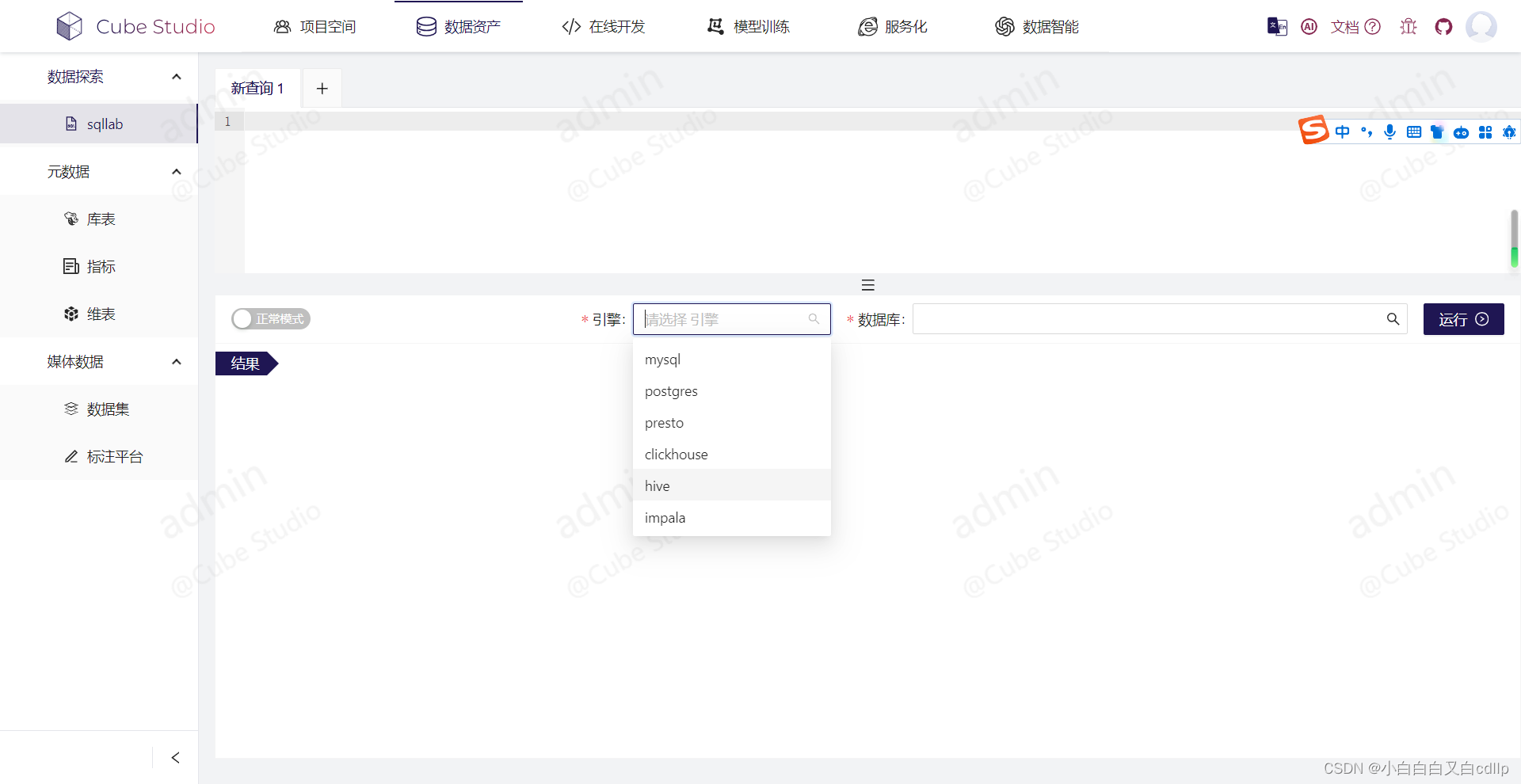
单门户上集成多种数据库查询入口
(作者:陈玓玏) 开源项目,欢迎star哦,https://github.com/tencentmusic/cube-studio 在一家公司,我们通常会有多种数据库,每种数据库因为其特性承担不同的角色,比如mysql这种轻量…...

华芯微特SWM34-使用定时器捕获快速解码EV1527编码
在无线应用领域,很多433Mhz和315Mhz的遥控器,红外探测器,门磁报警器,无线门铃等都使用EV1527编码格式来发射数据。发射和接收均有对应的RF芯片完成,而且成本极低(目前市场价3毛钱不到)。接收芯片…...
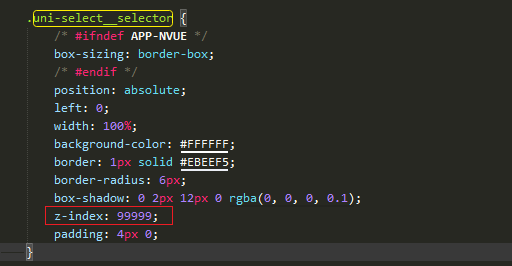
小程序安卓手机点击uni-data-select 下拉框选择器会出现蓝色阴影
解决方法:在导入的包中找到uni-data-select.vue,接着找到.uni-stat__select样式,把cursor: pointer去掉。 如果出现穿透问题,uni-select__selector的z-index加高,默认是2。...
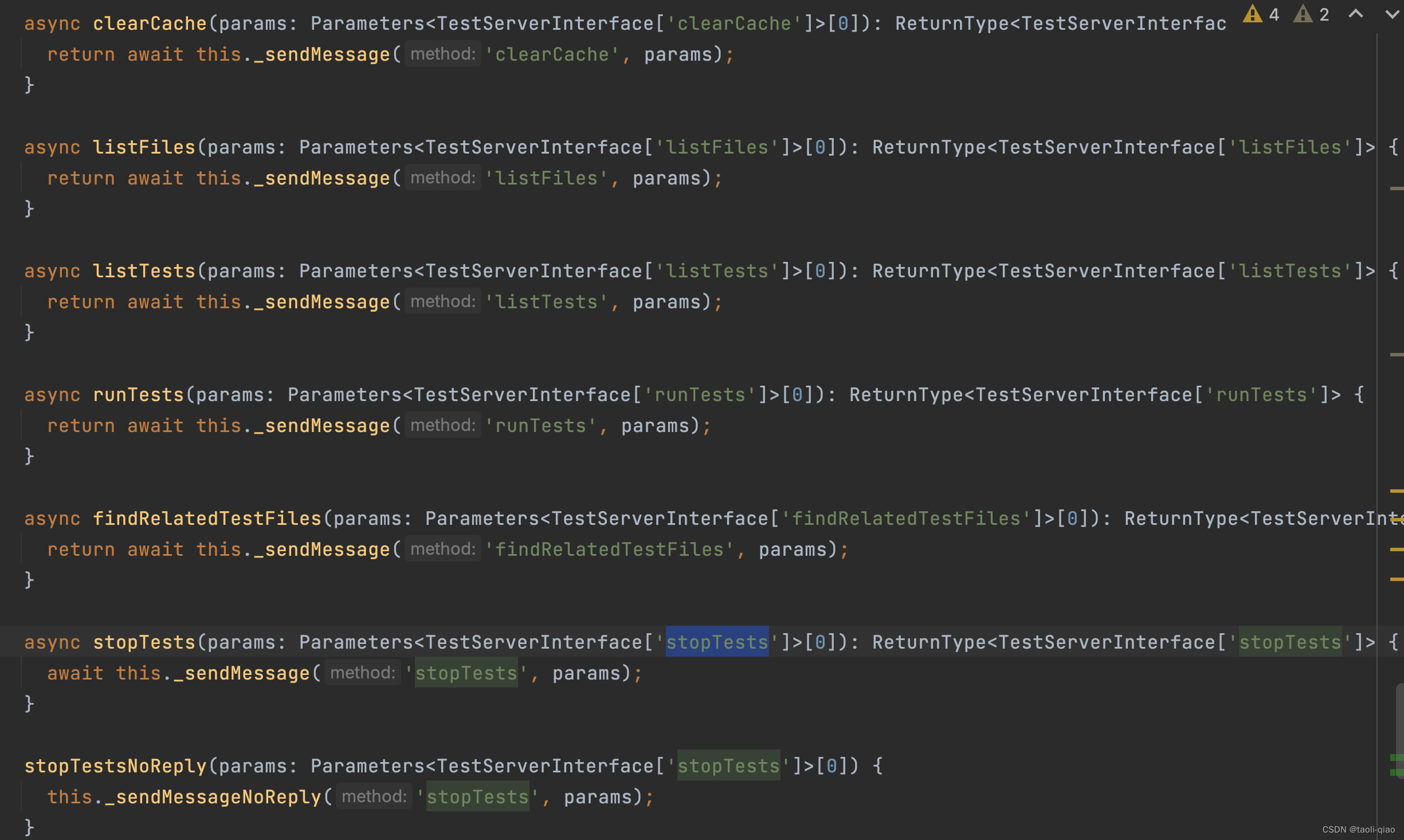
playwright vscode 插件源码解析
Playwright vscode插件主要功能 Playwright是微软开发的一款主要用于UI自动化测试的工具,在vscode中上安装playwright vscode插件,可以运行,录制UI自动化测试。 playwright vscode插件主要包括两块功能,功能一是在Test Explorer中…...
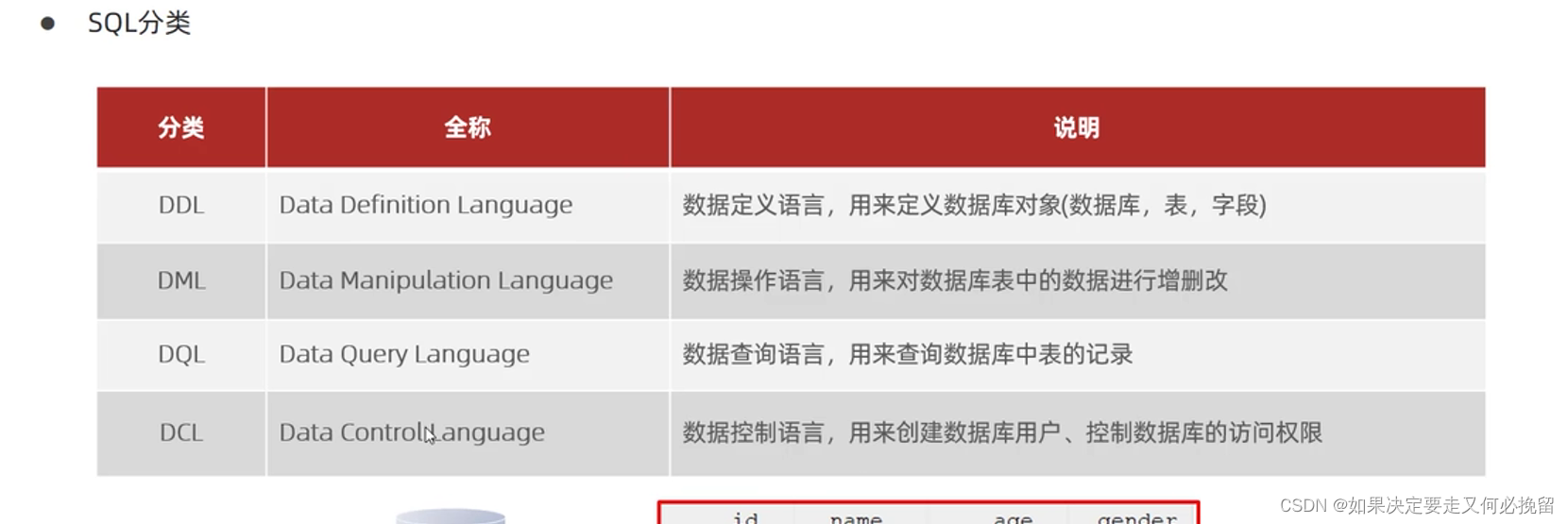
Mysql: SQL-DDL
一.SQL通用语法 1.SQL可以单行或者多行书写,以分号结尾。 2.SQL语句可以使用空格/缩进来增强语句的可读性。 3.MySQL数据库的SQL语句不区分大小写,关键字建议用大写。 4.注释: 单行注释:注释内容或#注释内容(Mysql特有) 多行注释:/*注释内容*/ 二.SQL分类 1.D…...

Java中的加密与解密:实现安全的数据传输
Java中的加密与解密:实现安全的数据传输 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在当今信息安全至关重要的时代,保护数据的安全性…...

基于SSM的美食推荐系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SSM的美食推荐系统,java项目。 ecli…...

Pycharm利用Anaconda环境
创建环境 conda create --name d2l python3.11 -y 激活环境 conda activate d2l 配置环境 以torch环境为例 我们可以按如下⽅式安装PyTorch的CPU或GPU版本: pip install torch pip install torchvision 我们的下⼀步是安装d2l包,以⽅便调取本书中经…...

Python函数魔术:深入理解18个高级函数特性
今天,我们将一起探索那些让代码瞬间变得优雅而强大的高级函数。准备好,让我们一起揭开它们的神秘面纱吧! 1. map():一招制胜,批量操作 想象一下,你需要给一个数字列表的每个元素加上5。普通的循环是不是让…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
