LeetCode题练习与总结:只出现一次的数字--136
一、题目描述
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1
示例 2 :
输入:nums = [4,1,2,1,2] 输出:4
示例 3 :
输入:nums = [1] 输出:1
提示:
1 <= nums.length <= 3 * 10^4-3 * 10^4 <= nums[i] <= 3 * 10^4- 除了某个元素只出现一次以外,其余每个元素均出现两次。
二、解题思路
这个问题可以通过异或(XOR)操作来解决。异或运算有几个特点:
- 任何数和0做异或运算,结果仍然是原来的数,即
a ⊕ 0 = a。 - 任何数和其自身做异或运算,结果是0,即
a ⊕ a = 0。 - 异或运算满足交换律和结合律,即
a ⊕ b ⊕ a = (a ⊕ a) ⊕ b = 0 ⊕ b = b。
根据以上性质,我们可以将数组中的所有元素进行异或运算。成对的元素异或的结果会是0,最终剩下的结果就是只出现一次的那个元素。
三、具体代码
class Solution {public int singleNumber(int[] nums) {int result = 0;for (int num : nums) {result ^= num;}return result;}
}
四、时间复杂度和空间复杂度
1. 时间复杂度
时间复杂度是指算法执行的时间随着输入数据量的增加而增长的速度。在这个问题中,我们关注的是算法执行的基本操作次数。
- 初始化操作:
int result = 0;这条语句执行了一次,因此它的复杂度是 O(1)。 - 循环操作:
for (int num : nums) { result ^= num; }这条循环语句会执行 n 次,其中 n 是数组nums的长度。循环体中的异或操作result ^= num是一个常数时间的操作,因此每次迭代的复杂度是 O(1)。 - 返回操作:
return result;这条语句执行了一次,因此它的复杂度是 O(1)。
总时间复杂度: 将所有操作的时间复杂度相加,我们得到总的时间复杂度是 O(1) + O(n) + O(1),由于 O(1) 可以忽略不计,因此总的时间复杂度是 O(n)。
2. 空间复杂度
空间复杂度是指算法在执行过程中临时占用存储空间的大小,它是输入数据量的大小的函数。在这个问题中,我们需要考虑算法中使用的额外空间。
- 变量空间:
int result;这条语句定义了一个整数变量result,它占用的空间是常数大小的,与输入数组nums的大小无关。因此,它的空间复杂度是 O(1)。
总空间复杂度: 将所有操作的空间复杂度相加,我们得到总的空间复杂度是 O(1)。
这个算法非常高效,因为它在线性时间内解决了问题,并且只使用了固定空间。
五、总结知识点
-
异或运算(XOR):这是代码中的核心概念。异或运算有几个关键特性:任何数与0异或结果为该数本身(
a ⊕ 0 = a),任何数与自身异或结果为0(a ⊕ a = 0),异或运算满足交换律和结合律(a ⊕ b ⊕ a = (a ⊕ a) ⊕ b = 0 ⊕ b = b)。这些特性使得异或运算可以用于解决只出现一次的元素问题。 -
数组的遍历:代码中使用增强型for循环(
for (int num : nums))来遍历数组nums中的每个元素。这是一种简洁的遍历数组元素的方式。 -
位操作:异或运算是一种位操作,它对两个数的每一位进行比较,如果相同则结果为0,不同则结果为1。位操作是解决许多算法问题的强大工具,尤其是在处理位级操作或优化空间复杂度时。
-
线性时间复杂度:代码中的循环确保了算法的时间复杂度为O(n),这意味着算法的运行时间与输入数组的大小成线性关系。
-
常量空间复杂度:代码中只使用了一个整数变量
result来存储最终结果,不随输入数组的大小而变化,因此算法的空间复杂度为O(1)。 -
算法设计:代码展示了如何利用数学性质来设计高效的算法。通过理解和应用异或运算的特性,可以在线性时间内找到只出现一次的元素,而不需要额外的空间。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:只出现一次的数字--136
一、题目描述 给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。 示例 1 : …...

常见的中间件都在解决什么问题?
常见的中间件都在解决什么问题 RocketMQ RocketMQ 是一款功能强大的分布式消息系统。 RocketMQ 源码地址:https://github.com/apache/rocketmq(opens new window) RocketMQ 官方网站:https://rocketmq.apache.org 什么场景下用 RocketMQ?…...

微信小程序-scroll-view实现上拉加载和下拉刷新
一.scroll-view实现上拉加载 scroll-view组件通过自身一些属性实现上拉加载的功能。 lower-threshold“100"属性表示距离底部多少px就会实现触发下拉加载的事件。 类似于在.json文件里面配置"onReachBottomDistance”: 100 bindscrolltolower"getMore"属…...

TS中interface和type的区别
在 TypeScript 中,interface 和 type 都可以用来定义对象的类型,但它们之间存在一些差异。 以下是 interface 和 type 的主要区别: 扩展(Extending): interface 可以通过 extends 关键字来扩展其他 interface。interfa…...
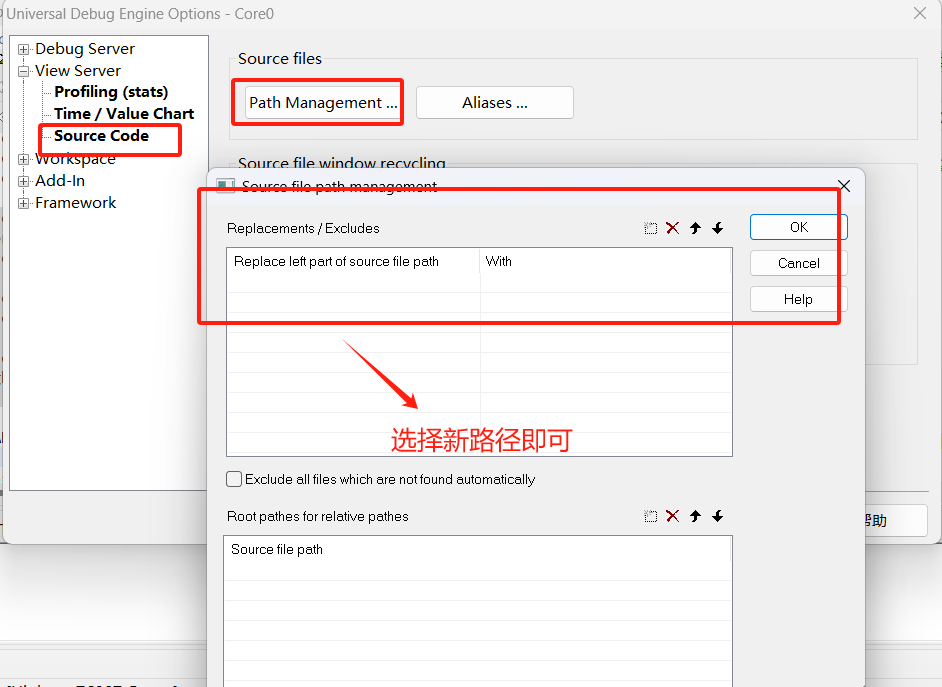
Hightec编译器系列之高级调试技巧精华总结
Hightec编译器系列之高级调试技巧精华总结 小T为了便于大家理解,本文的思维导图大纲如下: 之前可能很多小伙伴没有使用过Hightec编译器,大家可以参考小T之前的文章《Hightec编译器系列之白嫖就是爽》可以下载一年试用版本。 小T使用过适配英…...

【论文笔记】LoRA LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS
题目:LoRA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS 来源: ICLR 2022 模型名称: LoRA 论文链接: https://arxiv.org/abs/2106.09685 项目链接: https://github.com/microsoft/LoRA 文章目录 摘要引言问题定义现有方法的问题方法将 LORA 应用于 Transformer 实…...

【Sa-Token|4】Sa-Token微服务项目应用
若微服务数量多,如果每个服务都改动,工作量大,则可以只在网关和用户中心进行改动,也是可以实现服务之间的跳转。 这种方式可以通过在网关服务中生成和验证 Sa-Token,并将其与现有的 Token关联存储在 Redis 中。用户中心…...
】)
鸿蒙开发系统基础能力:【@ohos.hilog (日志打印)】
日志打印 hilog日志系统,使应用/服务可以按照指定级别、标识和格式字符串输出日志内容,帮助开发者了解应用/服务的运行状态,更好地调试程序。 说明: 本模块首批接口从API version 7开始支持。后续版本的新增接口,采用…...

SpringMVC系列十: 中文乱码处理与JSON处理
文章目录 中文乱码处理自定义中文乱码过滤器Spring提供的过滤器处理中文 处理json和HttpMessageConverter<T>处理JSON-ResponseBody处理JSON-RequestBody处理JSON-注意事项和细节HttpMessageConverter<T\>文件下载-ResponseEntity<T\>作业布置 上一讲, 我们学…...
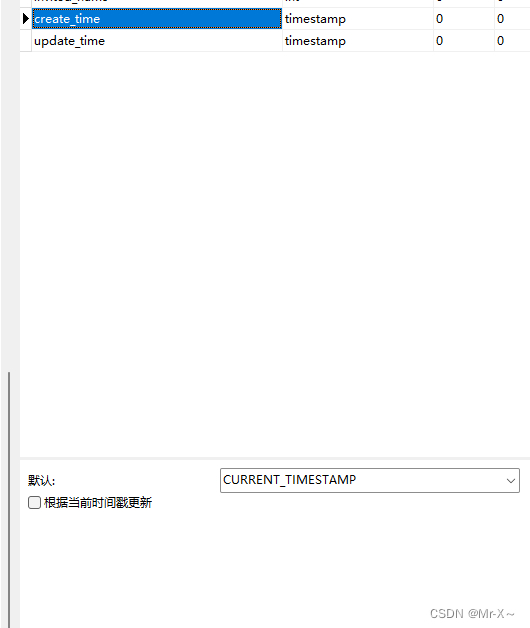
使用MyBatisPlus进行字段的自动填充
使用MyBatisPlus进行字段的自动填充 需求场景 当我们往数据库里面插入一条数据,或者是更新一条数据时,一般都需要标记创建时间create_time和更新时间update_time的值,但是如果我们每张表的每个请求,在执行sql语句的时候我们都手…...

python爬虫之aiohttp多任务异步爬虫
python爬虫之aiohttp多任务异步爬虫 爬取的flash服务如下: from flask import Flask import timeapp Flask(__name__)app.route(/bobo) def index_bobo():time.sleep(2)return Hello boboapp.route(/jay) def index_jay():time.sleep(2)return Hello jayapp.rout…...

1964springboot VUE小程序在线学习管理系统开发mysql数据库uniapp开发java编程计算机网页源码maven项目
一、源码特点 springboot VUE uniapp 小程序 在线学习管理系统是一套完善的完整信息管理类型系统,结合springboot框架uniapp和VUE完成本系统,对理解vue java编程开发语言有帮助系统采用springboot框架(MVC模式开发),…...

【前端项目笔记】3 用户管理
用户管理相关功能实现 涉及表单、对话框、Ajax数据请求 基本页面 用户列表开发 在router.js中导入Users.vue 解决用户列表小问题 选中(激活)子菜单后刷新不显示高亮 给二级菜单绑定单击事件,点击链接时把对应的地址保存到sessionSto…...
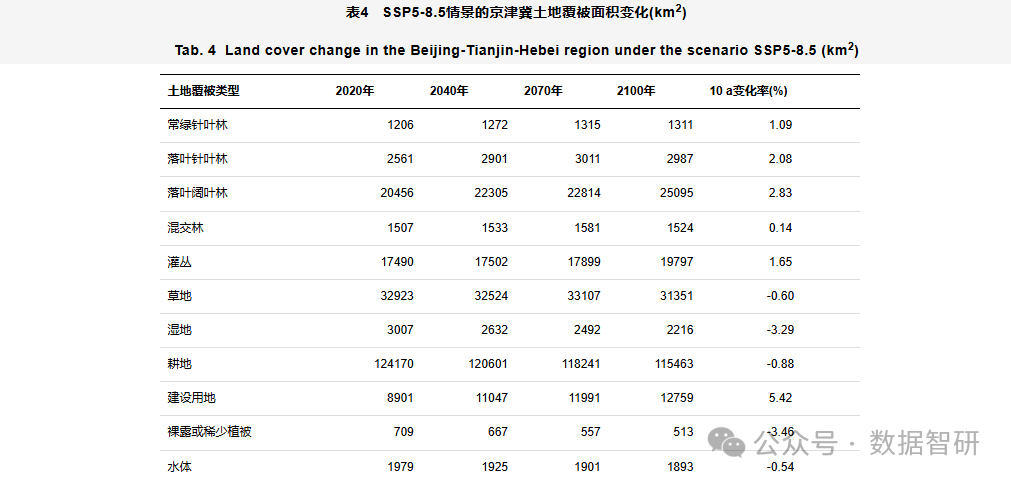
【文献及模型、制图分享】基于SSP-RCP不同情景的京津冀地区土地覆被变化模拟
公众号新功能 目前公众号新增以下等功能 1、处理GIS出图、Python制图、区位图、土地利用现状图、土地利用动态度和重心迁移图等等 2、核密度分析、网络od分析、地形分析、空间分析等等 3、地理加权回归、地理探测器、生态环境质量指数、地理加权回归模型影响因素分析、计算…...
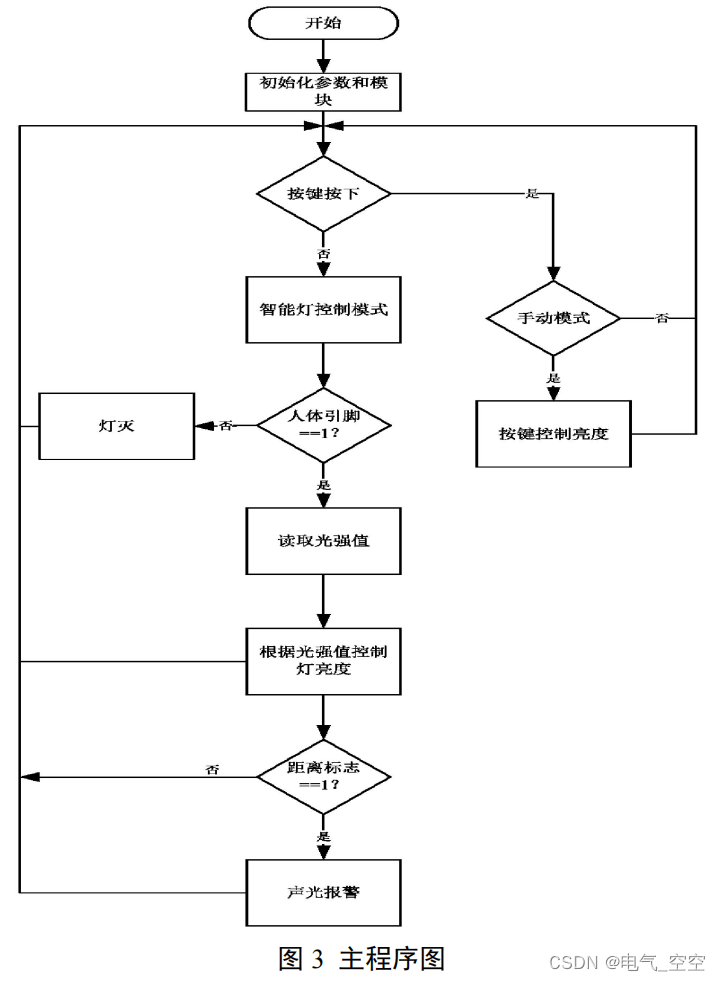
基于单片机的智能台灯控制系统
摘要: 文章设计一款单片机智能台灯控制系统,实现对台灯的手动和自动控制功能,以 STC89C52 单片机作为多功能智能台灯的主控制器,光电检测模块检测坐姿,红外传感器检测人体,光敏电阻检测光强,同…...

PrestaShop的一些使用介绍
目录 PrestaShop 是一个功能丰富的开源电子商务解决方案。 1. 以下是其基本概念和架构的一些要点: 2. PrestaShop 的模块开发是扩展其功能的重要方式。以下是对 PrestaShop 模块开发的详细介绍: 开发环境准备: 3. PrestaShop 的模块开发允…...

零基础女生如何入门人工智能,从哪里下手?学习时间大概要多久?
作为一个理工科早期毕业生,出于近乎本能的敏感,格外关注全网热议的ChatGPT。 本来国内就业环境就不好,各行各业内卷越来越严重,加上人工智能的异军突起,各行各业势必将迎来科技进步跨时代的巨大冲击,在此情…...

简答分享python学习进修网站
一、网战推荐 CodeCombat 是一款网页编程游戏。这款编程游戏借鉴了游戏很多设计元素,游戏剧情十分丰富。Codecombat能够学习Python多种语言,这些语言能够运用到游戏设计、网页应用、app的开发上。 Checkio 是一个基于浏览器的游戏,你需要使…...
)
linux高级编程(I/O)
fputc int fputc(int c, FILE *stream); 功能: 向流中写入一个字符 参数: c:要写入的字符 stream:文件流指针 返回值: 成功返回写入的字符ASCII码值 失败返回EOF fgetc int fgetc(FILE *stream); 功能: 从流中读取一个字符 参数: stream:文件流…...

Java面试——认证与授权
X、常见面试题汇总 1、Shiro与SpringSecutity对比 1)Shiro的特点: Shiro 是 Apache 下的项目,相对简单、轻巧,更容易上手使用。 Shiro 权限功能基本都能满足,单点登录都可以实现。且不用与任何的框架或者容器绑定, 可…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
