数据结构与算法:回溯算法约束条件:剪枝详解、示例(C#、C++)与回溯典型例题详解
文章目录
- 一、约束条件
- 二、剪枝
- 三、典型例题
- 四、常用术语
- 五、示例
- N 皇后问题 C# 示例
- N 皇后问题 C++ 示例
- 六、常见用用回溯算法解决的问题汇总
- 组合问题:
- 图论问题:
- 棋盘游戏问题:
- 优化问题:
- 调度问题:
- 其他问题:
- 总结

回溯算法是一种通过探索所有可能的候选解来找出所有解的算法。在解决一些问题时,我们需要设置一些约束条件,以确保候选解的有效性。这些约束条件在算法中起着非常重要的作用,因为它们定义了一个问题的解空间。通常,我们会使用剪枝技术来减少搜索空间,以提高算法的效率。
本文将详细介绍回溯算法中的约束条件、剪枝技术以及一些典型的回溯问题,还会讨论一些常用的术语。
一、约束条件
在回溯算法中,约束条件是非常重要的,因为它们定义了一个问题的解空间。约束条件必须被满足,一个候选解才被认为是有效的。通常,这些约束条件在算法中被用来进行剪枝,即提前排除那些明显不可能产生解的候选解,从而减少搜索空间。
以 N 皇后问题为例,约束条件如下:
- 同一列上的两个皇后不能相互攻击。
- 同一斜线(对角线和反对角线)上的两个皇后不能相互攻击。
在 0-1 背包问题中,约束条件如下:
- 背包的总容量有限。
- 每个物品都有一个重量和价值。
二、剪枝
剪枝是回溯算法中用于减少搜索量的技术。有两种主要的剪枝技术:
-
前剪枝: 在搜索的早期阶段就排除一些不可能产生有效解的分支。例如,在解决 N 皇后问题时,如果一个皇后已经被放置在某个位置,那么与这个位置在同一行、同一列和同一对角线上的所有其他位置都不能放置皇后。
-
后剪枝: 在搜索的后期阶段消除那些已经确定不可能产生解的分支。例如,在解决 0-1 背包问题时,如果当前的总重量已经超过背包的容量,那么这个分支可以被剪掉,因为不可能产生一个更优的解。
三、典型例题
1. N 皇后问题: 在 N×N 的棋盘上放置 N 个皇后,使得它们不会相互攻击(即没有两个皇后在同一列、同一行或同一对角线上)。
2. 0-1 背包问题: 给定一组物品,每个物品有一个价值和一个重量,需要选择一些物品放入一个给定容量的背包中,使得背包内物品的总价值最大。
3. 旅行商问题(TSP): 给定一组城市和每两个城市之间的距离,找到一条最短的路径,访问每个城市一次并返回起点。
四、常用术语
1. 候选解: 一个潜在的解,它可能满足所有约束条件。
2. 有效解: 一个候选解,它满足所有约束条件,被认为是实际问题中的解。
3. 搜索空间: 所有可能候选解的集合。
4. 路径/分支: 从初始状态到某个状态的一系列决策的集合。
5. 深度优先搜索(DFS): 一种回溯算法的实现方式,它沿着一个分支深入到不能再深入为止,然后回溯到上一个分叉点继续搜索。
五、示例
下面是 N 皇后问题和 0-1 背包问题的 C# 和 C++ 示例代码。
N 皇后问题 C# 示例
using System;
using System.Collections.Generic;namespace NQueens
{class Program{static void Main(string[] args){int n = 8;SolveNQueens(n);}static void SolveNQueens(int n){int[] board = new int[n];bool[] columns = new bool[n];bool[] diag1 = new bool[2 * n - 1];bool[] diag2 = new bool[2 * n - 1];if (PlaceQueens(board, 0, columns, diag1, diag2)){Console.WriteLine("解决方案:");PrintBoard(board);}else{Console.WriteLine("没有找到解决方案。");}}static bool PlaceQueens(int[] board, int row, bool[] columns, bool[] diag1, bool[] diag2){if (row == board.Length){return true;}for (int col = 0; col < board.Length; col++){if (columns[col] || diag1[row - col + board.Length - 1] || diag2[row + col]){continue;}columns[col] = true;diag1[row - col + board.Length - 1] = true;diag2[row + col] = true;board[row] = col;if (PlaceQueens(board, row + 1, columns, diag1, diag2)){return true;}board[row] = 0;columns[col] = false;diag1[row - col + board.Length - 1] = false;diag2[row + col] = false;}return false;}static void PrintBoard(int[] board){for (int i = 0; i < board.Length; i++){for (int j = 0; j < board.Length; j++){Console.Write(board[j] == i ? "Q " : ". ");}Console.WriteLine();}}}
}
N 皇后问题 C++ 示例
#include <iostream>
#include <vector>using namespace std;void printBoard(const vector<vector<int>>& board) {for (const auto& row : board) {for (int column : row) {cout << column << " ";}cout << endl;}
}bool isSafe(const vector<vector<int>>& board, int row, int col, vector<bool>& columns, vector<bool>& diag1, vector<bool>& diag2) {for (int i = 0; i < row; i++) {if (board[i][col] == 1) {return false;}}for (int i = row, j = col; i >= 0 && j >= 0; i--, j--) {if (board[i][j] == 1) {return false;}}for (int i = row, j = col; i < board.size() && j < board[0].size(); i++, j++) {if (board[i][j] == 1) {return false;}}return true;
}bool solveNQueensUtil(vector<vector<int>>& board, int row, vector<bool>& columns, vector<bool>& diag1, vector<bool>& diag2) {if (row == board.size()) {printBoard(board);return true;}for (int col = 0; col < board[0].size(); col++) {if (isSafe(board, row, col, columns, diag1, diag2)) {board[row][col] = 1;columns[col] = true;diag1[row - col + board.size() - 1] = true;diag2[row + col] = true;if (solveNQueensUtil(board, row + 1, columns, diag1, diag2)) return true;board[row][col] = 0;columns[col] = false;diag1[row - col + board.size() - 1] = false;diag2[row + col] = false;}}return false;
}vector<vector<int>> solveNQueens(int n) {vector<vector<int>> board(n, vector<int>(n, 0));vector<bool> columns(n, false);vector<bool> diag1(2 * n - 1, false);vector<bool> diag2(2 * n - 1, false);solveNQueensUtil(board, 0, columns, diag1, diag2);return board;
}int main() {int n = 4;vector<vector<int>> board = solveNQueens(n);return 0;
}
六、常见用用回溯算法解决的问题汇总
回溯算法是一种深度优先搜索的变种,它适用于解决那些需要探索所有可能解的问题。这类问题通常具有递归结构,即一个问题的解空间可以被分解为多个子问题,每个子问题都是原问题的一部分。以下是一些可以用回溯算法解决的问题:
组合问题:
- 排列问题(Permutations):给定一组数字,找出所有可能的排列。
- 组合问题(Combinations):给定一组数字,找出所有可能的组合。
图论问题:
- 最小生成树(MST):在无向图中找到一个包含所有顶点的子图,使得边的总权重最小。
- 最大匹配(Maximum Matching):在图中发现最大的匹配集合。
- 哈密顿路径(Hamiltonian Path):在图中寻找一条经过所有顶点恰好一次的路径。
- 中国邮递员问题(Chinese Postman Problem):寻找一条经过所有边恰好一次的路径,使得总权重最小。
棋盘游戏问题:
- 八皇后问题(8 Queens):在 8x8 的棋盘上放置 8 个皇后,使它们互不攻击。
- 骑士巡游问题(Knight’s Tour):在棋盘上找到一条骑士访问所有方格恰好一次的路径。
优化问题:
- 0-1 背包问题(0-1 Knapsack Problem):给定一组物品,每个物品有一个价值和重量,选择一些物品放入一个给定容量的背包中,使得背包内物品的总价值最大。
- 旅行商问题(TSP):寻找一条最短的路径,访问每个城市恰好一次并返回起点。
- 表达式求值问题(Evaluate Expression):给定一个包含加、减、乘、除和括号的表达式,计算其值。
调度问题:
- 课程调度问题(Course Scheduling):在有限的时间内安排多门课程,满足各种约束条件。
- 机器调度问题(Machine Scheduling):在有限的时间内安排多个机器的工作任务,满足各种约束条件。
其他问题:
- 子集和问题(Subset Sum):给定一个整数数组和一个目标值,判断是否存在一个子集,其和等于目标值。
- 数独问题(Sudoku):在 9x9 的网格中填入数字,使得每行、每列和每个 3x3 子网格中都包含 1 到 9 的所有数字。
- 汉诺塔问题(Tower of Hanoi):通过移动盘子从一个塔到另一个塔,同时遵守特定的规则。
回溯算法通过递归地尝试所有可能的解,并在发现当前解不满足要求时回溯到上一个状态,尝试其他可能的解。这种方法适用于解决上述问题,并且可以通过剪枝技术来优化搜索过程,减少不必要的计算。
总结
回溯算法是一种强大的算法,可以用来解决各种问题。通过设置约束条件和使用剪枝技术,我们可以有效地减少搜索空间,提高算法的效率。在实际应用中,回溯算法可以帮助我们解决各种问题,如 N 皇后问题、0-1 背包问题、旅行商问题等。希望这篇博客能帮助你更好地理解回溯算法及其应用。
相关文章:

数据结构与算法:回溯算法约束条件:剪枝详解、示例(C#、C++)与回溯典型例题详解
文章目录 一、约束条件二、剪枝三、典型例题四、常用术语五、示例N 皇后问题 C# 示例N 皇后问题 C 示例 六、常见用用回溯算法解决的问题汇总组合问题:图论问题:棋盘游戏问题:优化问题:调度问题:其他问题: …...

利用sortablejs实现拖拽排序
import Sortable from "sortablejs";created() {//禁止火狐拖拽进行搜索document.body.ondrop function(event){event.preventDefault();event.stopPropagation();}}// 打开对话框的时候调用下openCustomDialog(){this.rowDrop()}// 行拖拽 rowDrop() {this.$nextTi…...
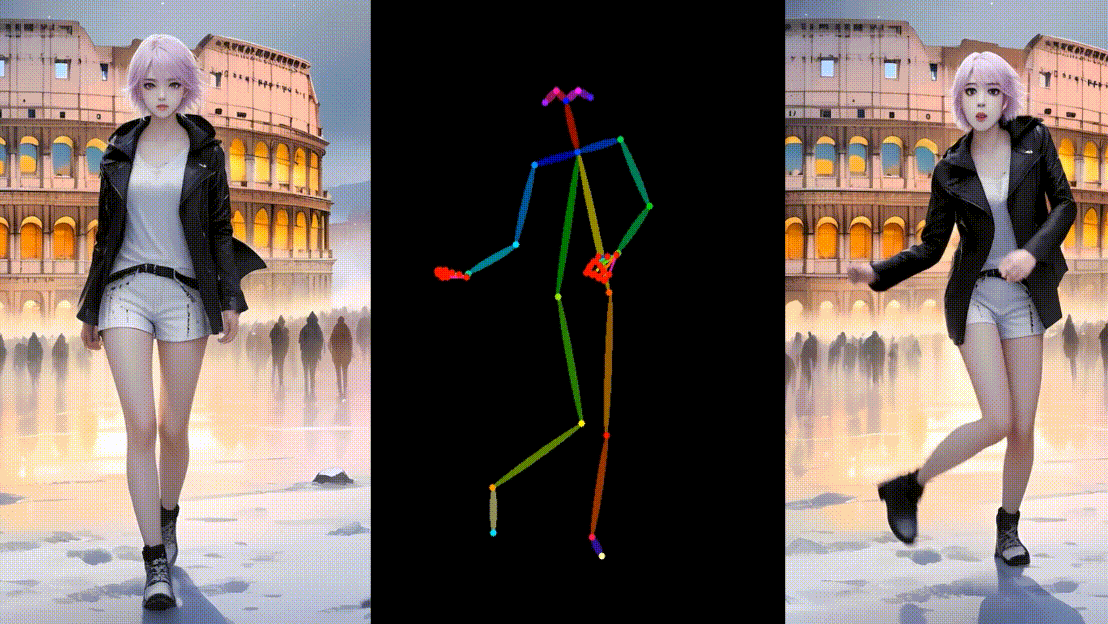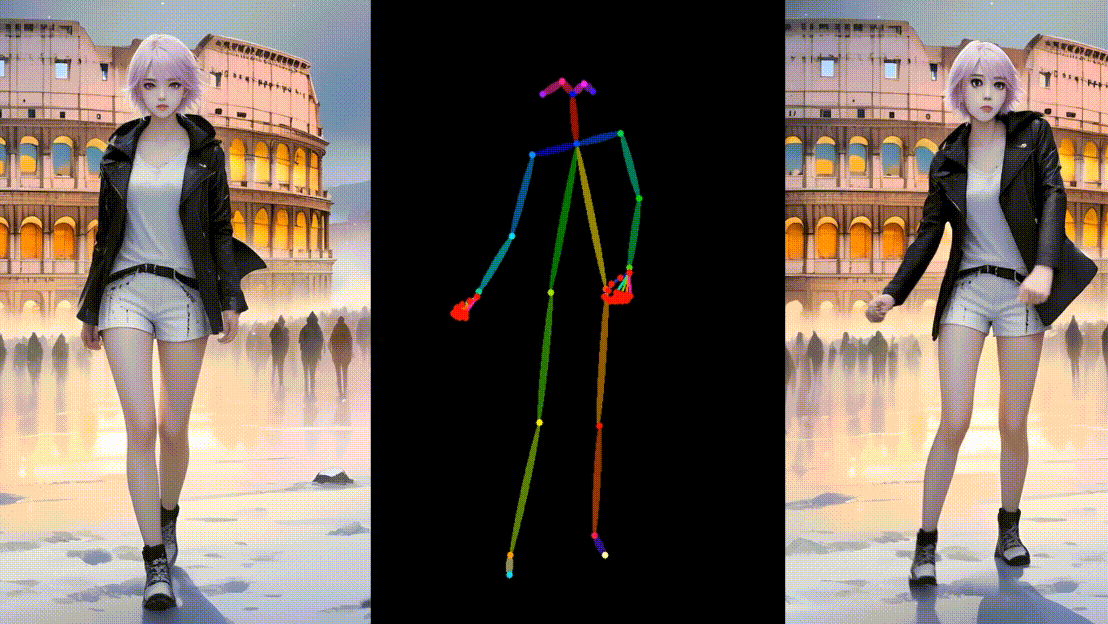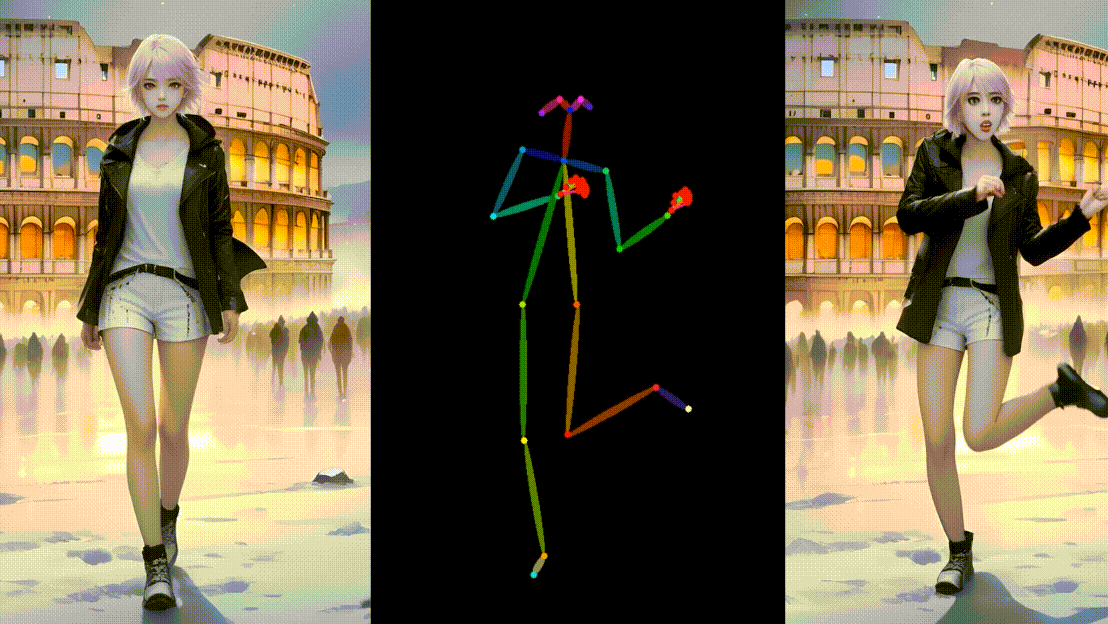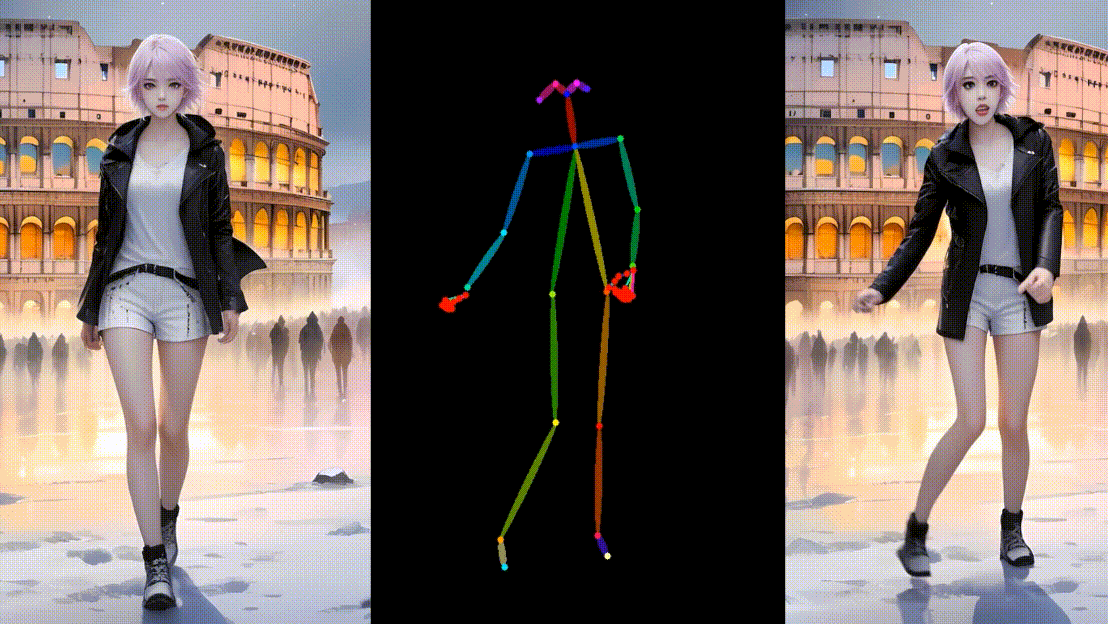
超越AnimateAnyone, 华中科大中科大阿里提出Unimate,可以根据单张图片和姿势指导生成视频。
阿里新发布的UniAnimate,与 AnimateAnyone 非常相似,它可以根据单张图片和姿势指导生成视频。项目核心技术是统一视频扩散模型,通过将参考图像和估计视频内容嵌入到共享特征空间,实现外观和动作的同步。 相关链接 项目࿱…...
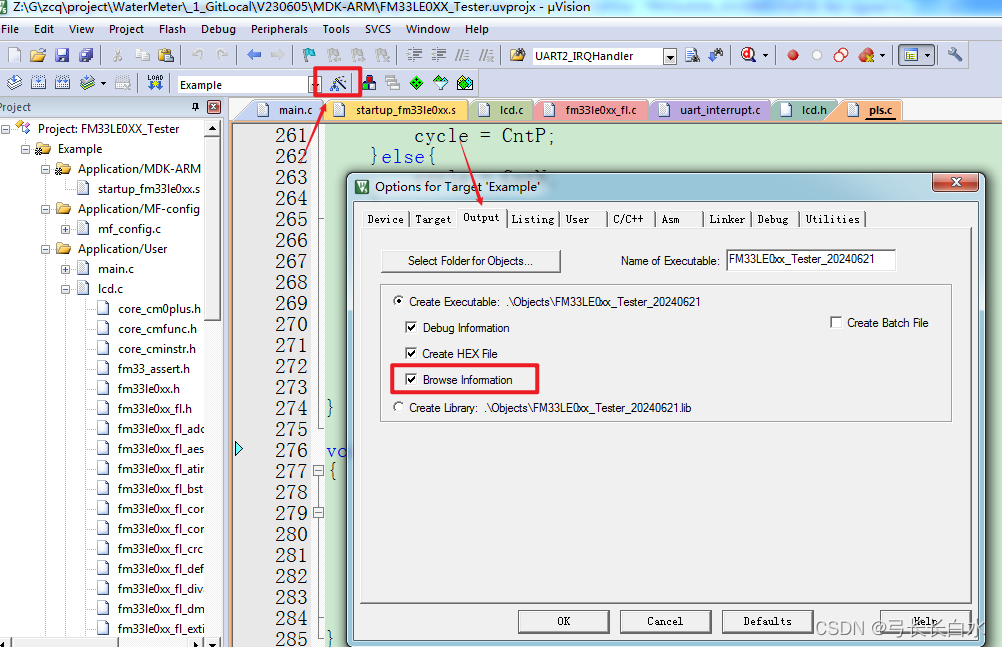
【MDK5问题】:MDK5无法跳转,并且提示:no browse information available in xxxxx
1、问题: MDK5原来的函数调用可以直接跳转到原函数,但是出现不能跳转原函数的情况,且提示:no browse information available in xxxxx 的情况; 2、解决: 如下图所示:在魔术棒(pro…...
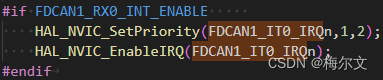
OS中断机制-外部中断触发
中断函数都定义在中断向量表中,外部中断通过中断跳转指令触发中断向量表中的中断服务函数,中断指令可以理解为由某个中断寄存器的状态切换触发的汇编指令,这个汇编指令就是中断跳转指令外部中断通过在初始化的时候使能对应的中断服务函数如何判断外部中断被触发的条件根据Da…...

LabVIEW如何进行电磁兼容性测试
电磁兼容性(EMC)测试是确保电子设备在其工作环境中能够正常运行且不会对其他设备产生有害干扰的关键步骤。LabVIEW作为一种强大的系统设计和开发工具,可以有效地用于电磁兼容性测试。以下是如何使用LabVIEW进行电磁兼容性测试的详细步骤和方法…...

Spring底层架构核心概念总结
Spring底层架构核心概念总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! Spring框架是Java企业级应用开发中最受欢迎的框架之一。它以其强大的依赖注入&am…...
hex、bin、elf、s19等文件格式介绍以及格式转换
文章目录 前言一、bin文件二、hex文件数据记录格式扩展线性地址记录(HEX386)格式扩展段地址记录(HEX86)文件结束(EOF)记录三、elf文件四、S19文件五、不同格式之间转换将bin文件转换成hex文件将hex文件转换成bin文件将bin文件转换成s19文件前言 编译器或汇编器将程序的源代码(…...

oracle 窗口函数使用
Oracle 数据库中的窗口函数(也称为分析函数或OLAP函数)允许您对一组相关的行执行计算,而不是只针对单行。这些函数在数据分析中特别有用,因为它们允许您执行诸如计算移动平均值、累积总和、百分比排名等操作。 以下是一些常用的 …...

【Git】git常用命令
初始化配置 设置用户名和邮箱,来标识身份,方便日后上传GitHub git config --global user.name "xxx" git config --global user.email "xxx"git config --global --list # 存用户名和密码 git config --global --list # 查看配置新…...
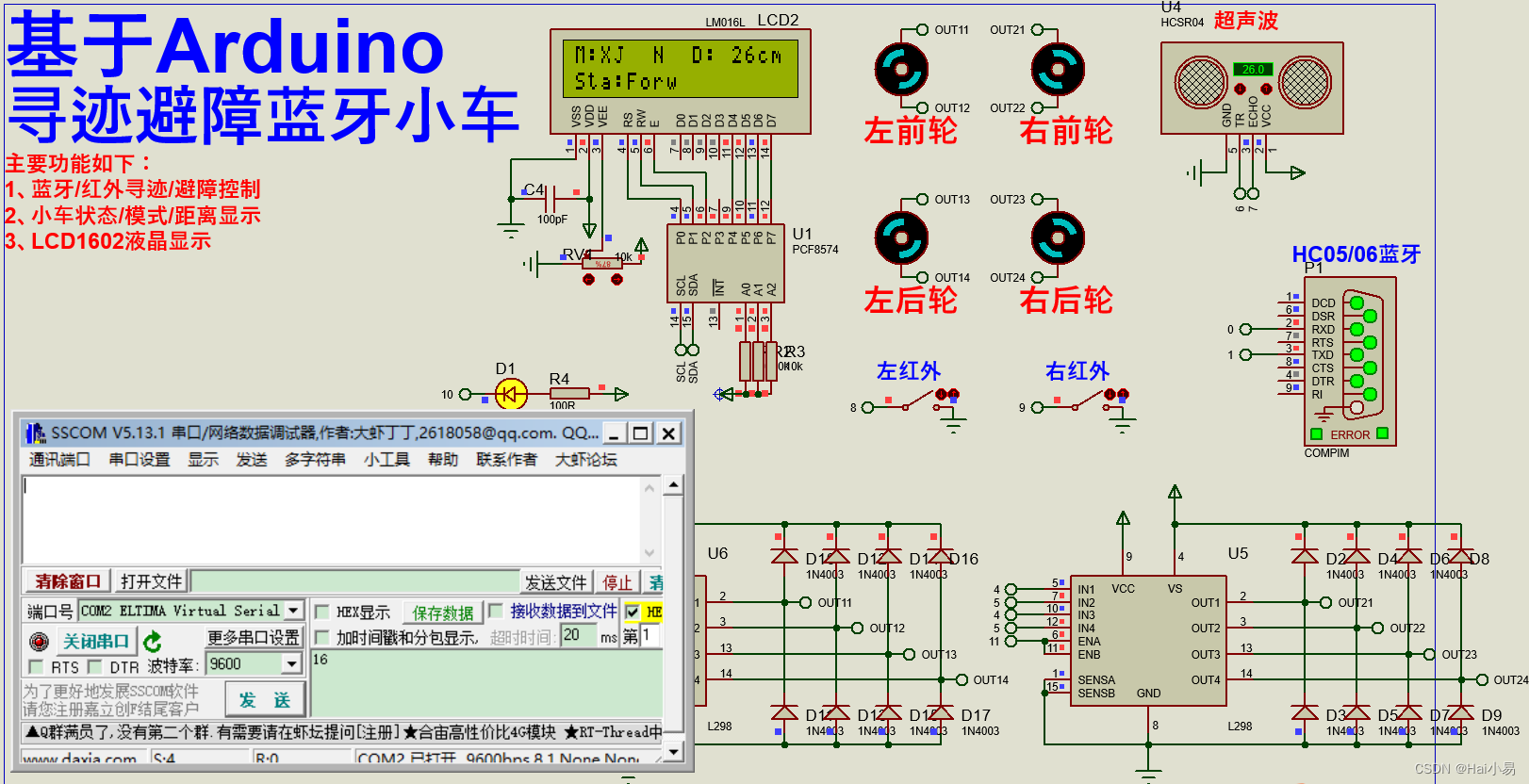
【Proteus仿真】【Arduino单片机】寻迹避障蓝牙遥控小车
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真Arduino单片机控制器,使LCD1602液晶,L298电机,直流电机,HC05/06蓝牙模块,HCSR04超声波,红外寻迹模块等。 主…...
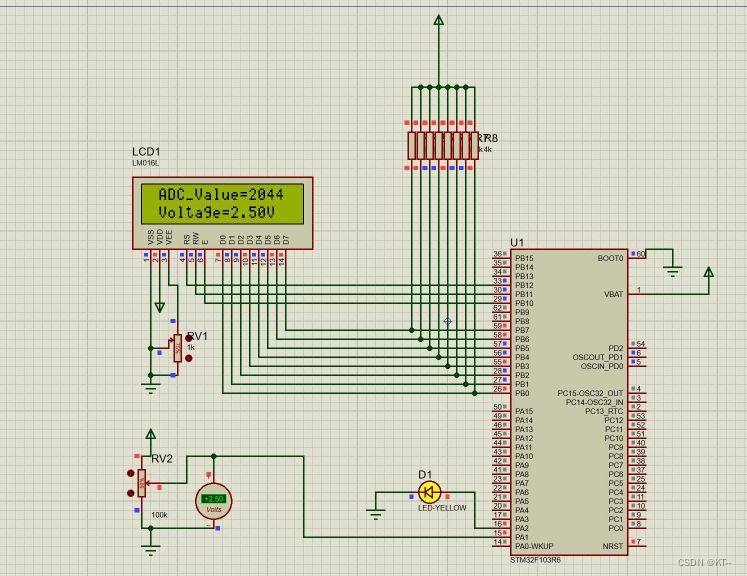
嵌入式实验---实验八 ADC电压采集实验
一、实验目的 1、掌握STM32F103ADC电压采集程序设计流程; 2、熟悉STM32固件库的基本使用。 二、实验原理 1、使用STM32F103R6采集可变电阻上的电压信号,并通过计算把当前ADC转换值和电压值显示在LCD1602液晶屏上; 2、对照电压表读数&…...

PHP框架详解:Symfony框架的深度剖析
PHP框架详解:Symfony框架的深度剖析 摘要: Symfony是当前最受欢迎的PHP框架之一,它以其强大的功能和灵活性而闻名。本文将详细介绍Symfony框架的核心概念、架构、组件以及其实践应用,帮助读者深入理解这一框架的优势和使用场景。…...

Linux `screen` 命令详解与使用指南
Linux screen 命令详解与使用指南 在Linux系统中,screen 是一个非常有用的工具,它允许用户在单个终端会话中运行多个进程,并能在会话之间切换。screen 特别适用于远程登录(如通过SSH)时,确保即使网络连接断…...

CSRF绕过
目录 1. 检查referer referer绕过 2. 检查origin 3. Cookie检查 SameSite 持久性验证 4. Token检查 检测token编码类型,尝试篡改token 绕过token检测 在页面上尝试修改密码, 观察请求的格式. 绕过思路 1. 编写一个js脚本完成以下的任务: 2. 引诱登录的用户触发这…...

如何处理Java中的BufferOverflowException异常?
如何处理Java中的BufferOverflowException异常? 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在Java编程中,BufferOverflowExceptio…...

XMLTomcatHttp协议
XML&Tomcat&Http协议 目录 XML&Tomcat&Http协议 1. xml解析(了解) 1.1 配置文件 1.1.1 配置文件的作用 1.1.2 常见的配置文件类型 1.2 properties文件 1.2.1 文件示例 1.2.2 语法规范 1.3 XML文件 1.3.1 文件示例 1.3.2 概念介绍 1.3.3 XML的基本语…...

Lua优化技巧
常见的Lua优化小技巧 Lua常见优化点:1. 尽量使用局部变量2. table的相关减少对表的访问for循环预分配表空间元表 3. string的相关4. 避免运行时加载编译5. 尽量避免频繁创建临时对象闭包表 Lua常见优化点: 1. 尽量使用局部变量 尽量将变量局部化&#x…...

探索CSS中的cursor鼠标属性
在网页设计中,细节决定成败。CSS的cursor属性是这些细节中的关键一环,它不仅影响着网页的美观,更关乎用户体验。今天,我们就来深入了解一下cursor属性,看看如何通过它来增强网页的交互性。 cursor属性概览 cursor属性…...

图象去噪1-使用中值滤波与均值滤波
1、中值滤波 使用中值滤波去除图像的异常像素点,使用cv2.cv2.medianBlur(img, 3)表示再图像在中值滤波窗口3*3的范围内,从下到大排序,将当前值替换为排序中值(如下图所示)将56替换为(56,66,90,…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
