二叉树第一期:树与二叉树的概念
一、树
1.树的定义
与线性表不同,树是一种非线性的数据结构,由N(N>=0)个结点组成的具有层次关系的集合;因其形状类似生活中一颗倒挂着的树,故将其数据结构称为树。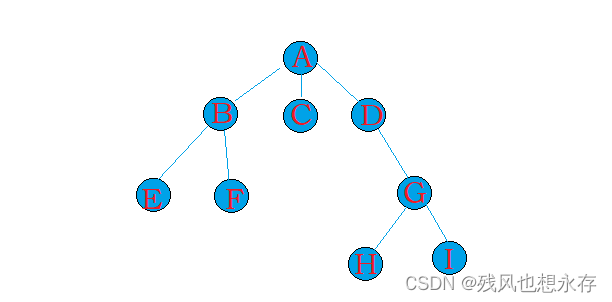
2.树的相关概念
| 根结点 | 没有前驱的结点,称为根结点 |
|---|---|
| 子树 | 以某个结点为根结点的所有后代结点(包括此结点),为该结点的子树,例如B、E、F组成的树,是A的子树 |
| 结点的度 | 某个结点后继结点的个数,称为结点的度 |
| 叶(终端)结点 | 某个结点后继结点的个数为0,称为叶结点 |
| 分支(非终端)结点 | 某个结点后继结点的个数非0,称为分支结点 |
| 双亲(父)结点 | 某个结点的前驱结点,称为该结点的双亲结点 |
| 孩子(子)结点 | 某个结点的后继结点,称为该结点的孩子结点 |
| 兄弟结点 | 某两个结点的前驱结点相同,则称为兄弟结点 |
| 堂兄结点 | 某两个结点在同一个层次上,称为,堂兄结点 |
| 祖先 | 某个结点到根结点的一条路线上的结点,统称为该结点的祖先 |
| 子孙 | 某个结点的所有后代结点,统称为该结点的子孙 |
| 树的度 | 最大的结点的度,称为树的度 |
| 树的高度(深度) | 根结点到叶结点,所经过结点的个数,最大的,称为树的高度,或深度 |
| 结点的层级 | 某结点与根结点连线,所含义的结点个数 |
| 森林 | M(M>=2)个互不相交的树,称为森林 |
总结:
- 一个树,其任意子树是互不相交的,否则就不叫树,而是图,这一树形结构,如B、C、D为根组成的树,不存在相交情况。
- 任意一个树都可以看成根和子树,子树又可以看成,根和子树,所以树这一结构,是由递归搭建的。
3.树的表示
对树这一结构,有明确的了解后,又有一个新的问题,我们该如何的去表示的树的结构呢?常见的有孩子表示法,双亲表示法,孩子双亲表示法,孩子兄弟表示法;这里将介绍最好理解的孩子表示法,和优点明显的孩子兄弟表示法
i.孩子表示法
#define MAX 10 // 已知树的最大的深度typedef int TDatetype;typedef struct Tree
{TDatetype date;struct Tree* child[MAX];
}Tree;ii.左孩子右兄弟表示法
typedef int TDatetype;typedef struct Tree
{TDatetype date;struct Tree* child;struct Tree* brother;
}Tree;4.树的实际应用
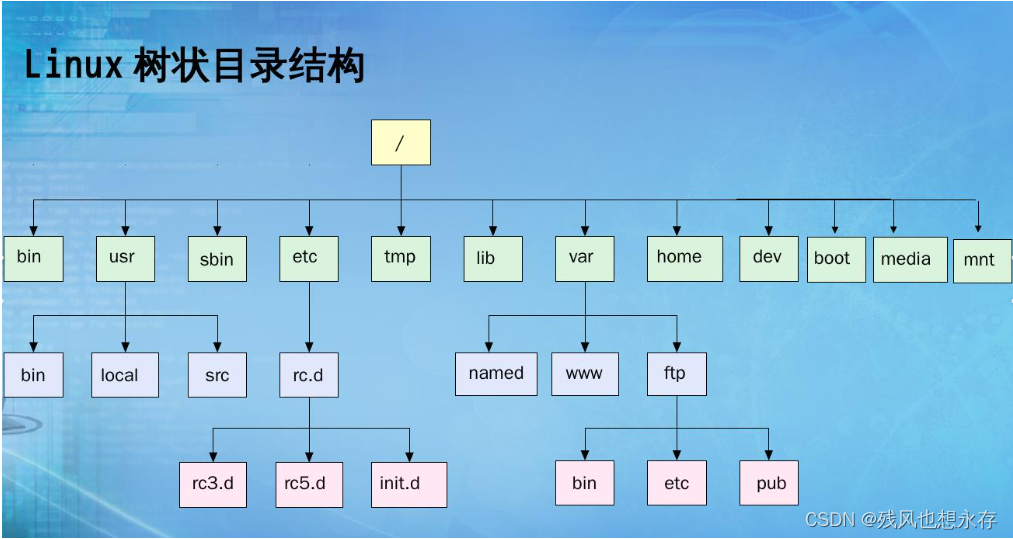
我们文件的存储方式就是以树这一结构存储,每一个盘即为一个树,所有盘则组成一个森林,下面则是Linux系统下,文件的存储结构。
二、二叉树
1.二叉树的定义
在树的定义基础上,树的度最大不超过2的(每个结点的度最大不超过2的),即为二叉树。(注:二叉树有左孩子右孩子之分)
2.特殊的二叉树
i.满二叉树
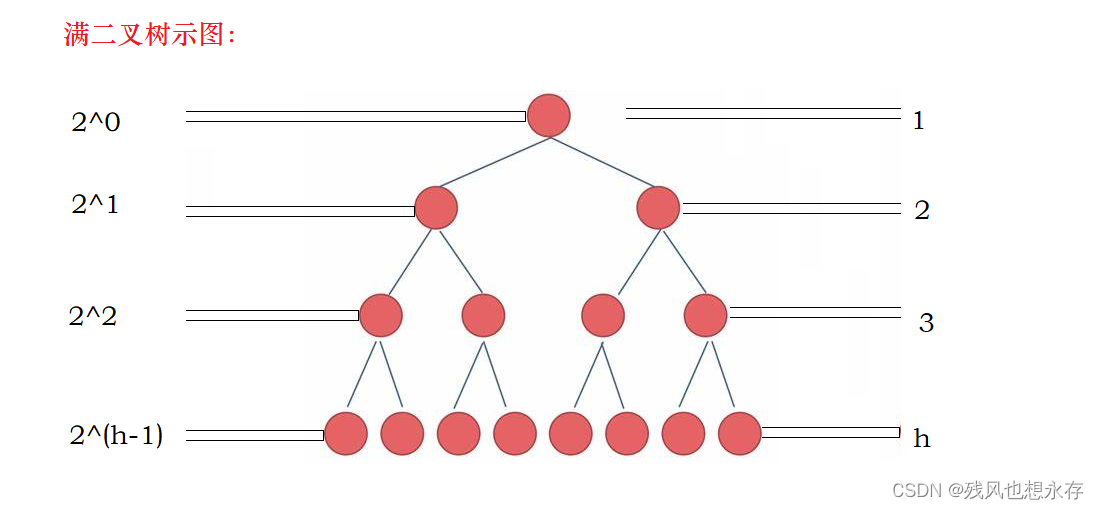
满二叉树的定义:树的深度为h,每一层都达到含有结点的最大个数,即第x(0<x<=h)层,结点个数 = 2^(x-1);
ii.完成二叉树
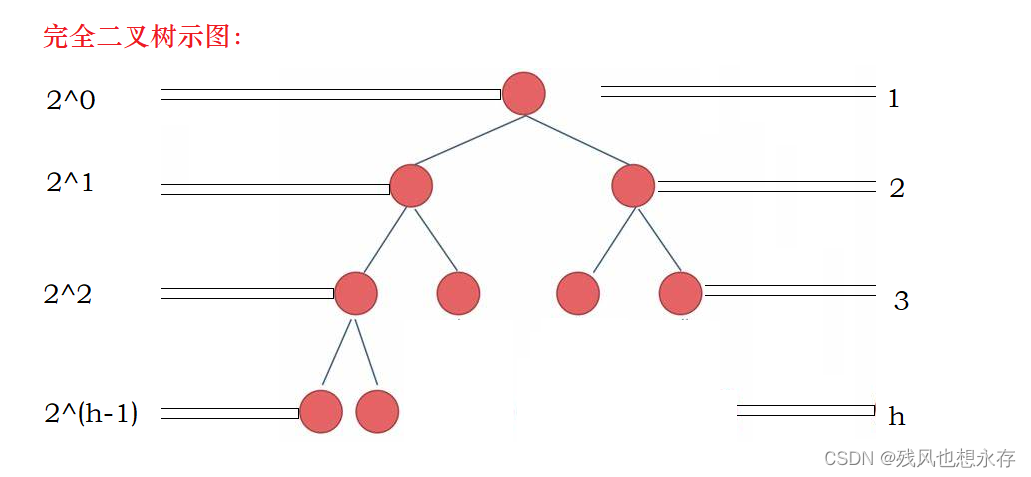
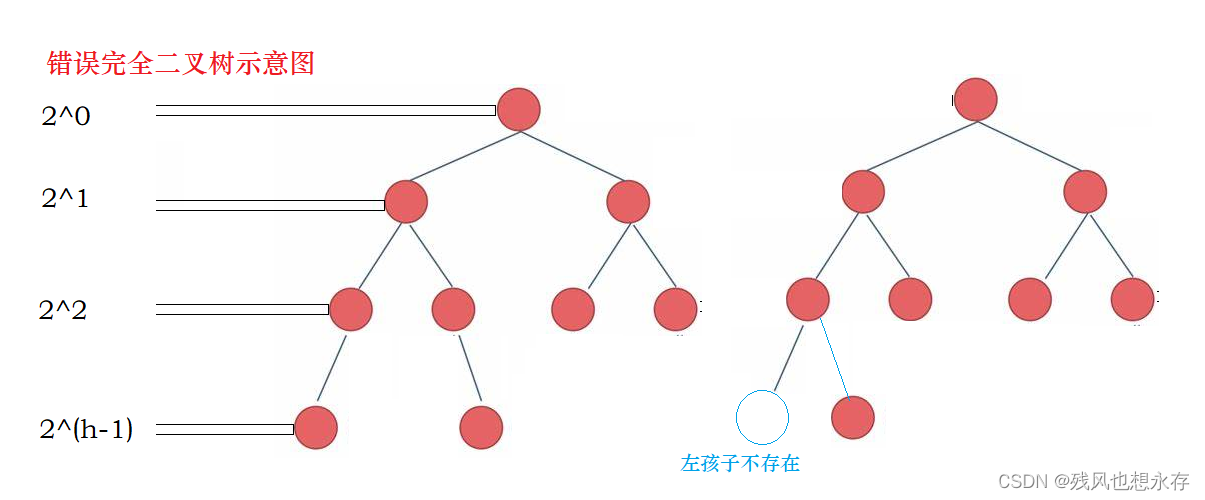
完全二叉树的定义:树的深度为h,前h-1层,结点个数达到最大值,第h层,从左到右有连续的结点。
3.二叉树的性质
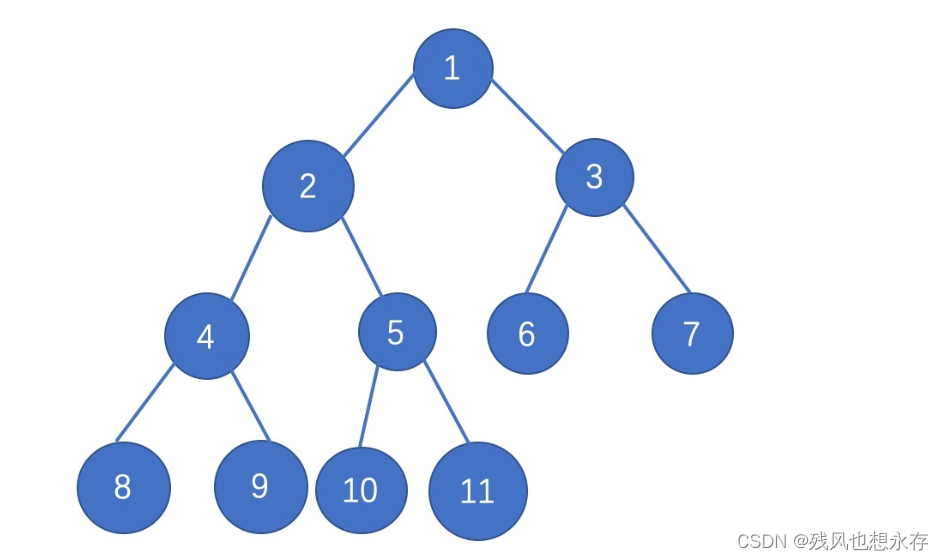
- 第H层结点个数:2^(H-1)
- 高度为H的二叉树,所含有结点个数的最大值为2^H-1
- N个结点的满二叉树,其高度为以2为底,log(N+1)
- N个结点的完全二叉树,其高度为以2为底,log(N+X+1),X为相同高度的满二叉树与完全二叉树的结点个数差的绝对值
- 终端结点的个数 = 度为2的结点个数 + 1
4.二叉树的表示
i.二叉树的顺序结构
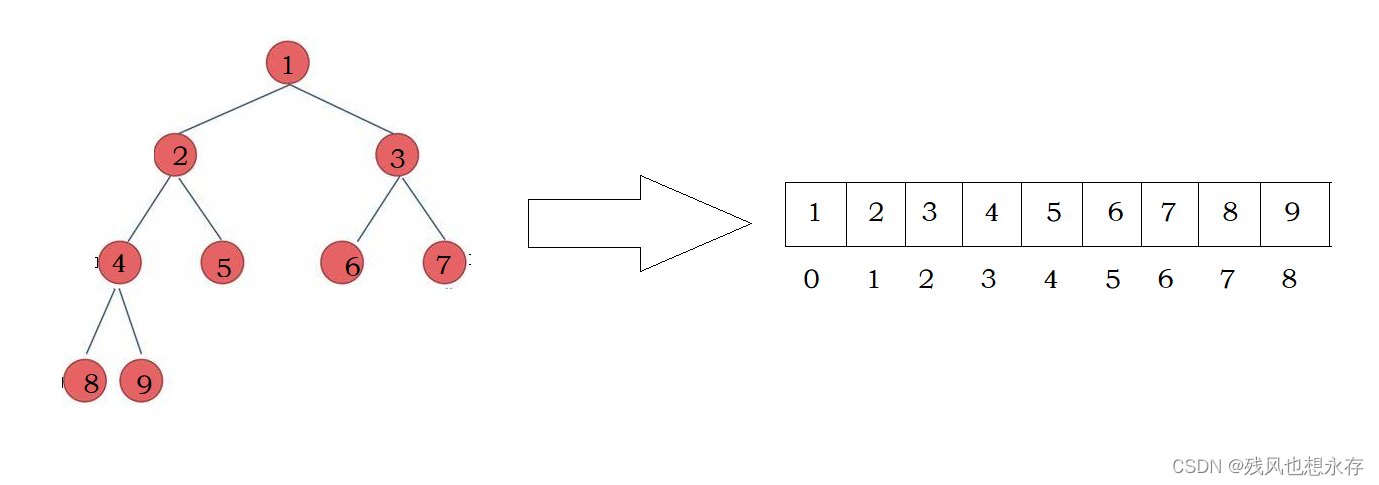
二叉树的顺序结构:将一颗二叉树的数据,以层为顺序,依次存储在数组中(保留空结点的位置)。
typedef int BTDateType; // 重定义树的数据类型typedef struct BinaryTree
{BTDateType* date; // 动态顺序表int size; // 当前顺序表存储数据的个数int capacity; // 当前顺序表的容量大小
}BinaryTree;
为什么要这么设计呢?
因为我们通过数组下标,可以得出其父亲或者两个孩子的结点位置;
- 某结点左孩子的下标 = 该结点的下标 * 2 + 1
- 某结点右孩子的下标 = 该结点的下标 * 2 + 2
- 某结点的父亲下标 = (该结点的下标 - 1) / 2
读者,若不相信,可以以上面示图为例子,代入数据,进行自我验证!!!
- 根据此特性,
- 首先:我们就可以理解了,为什么要留着空结点的位置,而不是直接把数据依次存入~
- 最后:可以得出结论适合于存储完全二叉树,而不适合存储普通二叉树,因为普通二叉树,会造成大量的空间浪费。
ii.二叉树的链式结构
二叉树的链式结构,声明如下:孩子不存在,则用NULL表示;
typedef int BTDatetype;typedef struct BinaryTree
{BTDatetype date; // 数据struct Tree* lift; // 左孩子struct Tree* right; // 右孩子
}BT;
相关文章:

二叉树第一期:树与二叉树的概念
一、树 1.树的定义 与线性表不同,树是一种非线性的数据结构,由N(N>0)个结点组成的具有层次关系的集合;因其形状类似生活中一颗倒挂着的树,故将其数据结构称为树。 2.树的相关概念 根结点 没有前驱的结点,称为根…...

vue跨域问题,请注意你的项目是vue2还是vue3
uniapp跨域设置了,但还是有问题 uniapp设置代理后还是无法请求后端接口vue2项目设置代理vue3项目设置代理 uniapp设置代理后还是无法请求后端接口 如果你在possman,apifox上测试接口都没有问题,但是在hbuild项目中设置代理后,还是…...
大厂晋升学习方法一:海绵学习法
早晨 30 分钟 首先,我们可以把起床的闹钟提前 30 分钟,比如原来 07:30 的闹钟可以改为 07:00。不用担心提前 30 分钟起床会影响休息质量,习惯以后,早起 30 分钟不但不会影响一天的精力,甚至可能反而让人更有精神。早起…...

【ARMv8/v9 GIC 系列 4.2 -- GIC CPU Interface 详细介绍】
文章目录 GIC CPU Interface 介绍CPU Interface 主要寄存器 GIC CPU Interface 介绍 A 系列处理器提供 5个管脚来实现中断,分别是: nIRQ:物理普通中断nFIQ:物理快速中断nVIRQ:虚拟普通中断nVFIQ:虚拟快速…...

小抄 20240619
1 一个人内心充满恐惧的时候,就会开始信仰一个至高的东西来追求道德上的确定感。 然后会向外看,去指责那些自己不敢做但别人做到的,在他看来不道德的事。 2 之前说租房有不可能三角:房租低,离公司近,住着…...

【06】数据模型和工作量证明-工作量证明
1. 工作量证明的背景 比特币是通过工作量证明来竞争记账权,并获得比特币奖励。简单来讲就是谁能够根据区块数据更快的计算得到满足条件的哈希值,谁就可以胜出,这个块才会被添加到区块链中。我们把这个过程称为挖矿。比特币每10分钟产生1个区块。 2. 工作量证明算法 1. 获…...
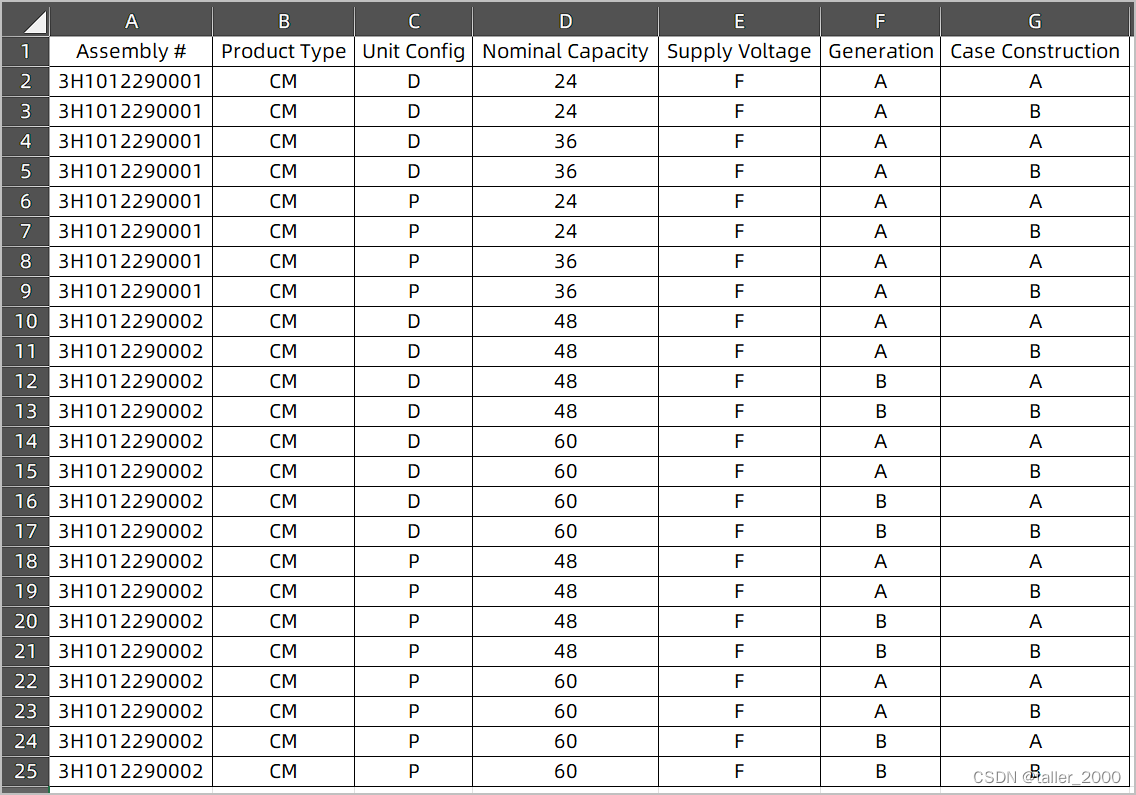
VBA递归过程快速组合数据
实例需求:数据表包含的列数不固定,有的列(数量和位置不固定)包含组合数据,例如C2单元格为D,P,说明Unit Config有两种分别为D和P,如下图所示。 现在需要将所有的组合罗列出来,如下所示…...
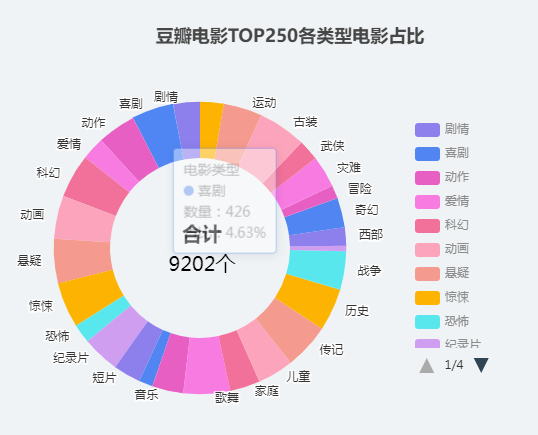
基于豆瓣电影TOP250的可视化设计
本文要完成的目的,实现豆瓣电影TOP250的可视化 思路 讲解思路,采用倒推的方式, 首先确定可视化图表,也就是最终的效果。这样就能确定需要那些基础数据根据需要的数据进行按需爬取存储。 本篇文章完成前两步。可视化图表设计 和 …...

YOLOv8中的C2f模块
文章目录 一、结构概述二、模块功能 一、结构概述 C2f块:首先由一个卷积块(Conv)组成,该卷积块接收输入特征图并生成中间特征图特征图拆分:生成的中间特征图被拆分成两部分,一部分直接传递到最终的Concat块,另一部分传递到多个Botleneck块进…...
)
ESP32 双线汽车接口 (TWAI)
一:TWAI概述 双线汽车接口 (TWAI) 是一种适用于汽车和工业应用的实时串行通信协议。它兼容 ISO11898-1 经典帧(CAN2.0),因此可以支持标准帧格式(11 位 ID)和扩展帧格式(29 位 ID&#x…...
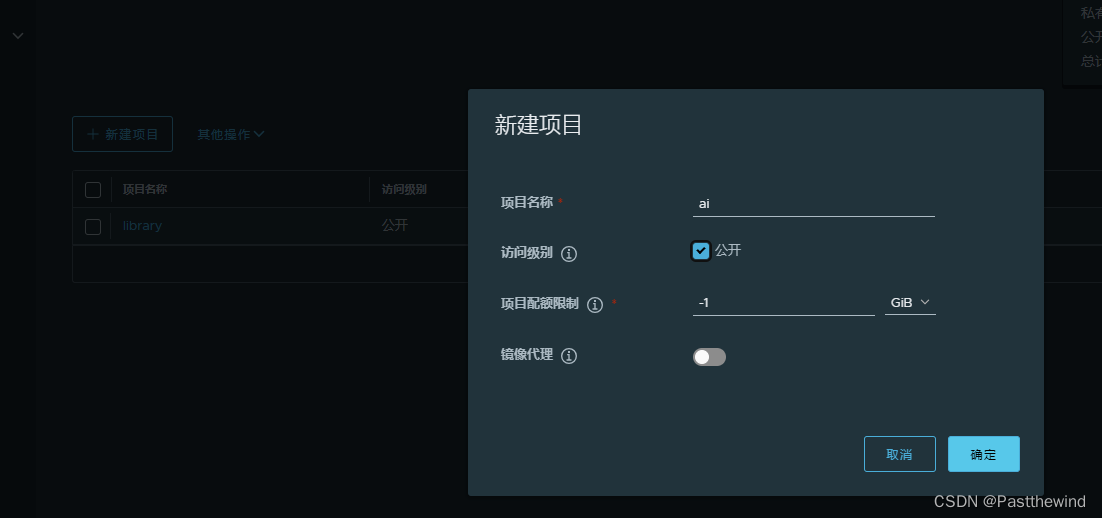
docker-compose离线安装harbor
1、下载harbor goharbor下载:Releases goharbor/harbor GitHub harbor-offline-installer-v2.11.0.tgz 2、解压 tar -xvf harbor-offline-installer-v2.11.0.tgz 3、创建一个卷目录,并复制一份配置文件 cd harbor; mkdir data;cp harbor.yml.tmp…...
)
服务器“雪崩”的常见原因和解决方法 (C++)
在C服务器编程中,"雪崩"现象指的是服务器在高并发请求的情况下,由于资源(如线程、文件描述符、内存等)耗尽或锁争用等问题,导致服务器性能急剧下降,甚至完全失去响应的情况。这种现象会连带影响其…...

详解ES6中的类、对象和类的继承
在ES6(ECMAScript 2015)之前,JavaScript 并没有像其他面向对象的编程语言那样的类(class)的概念。相反,它使用了一种基于原型的继承模型来实现面向对象编程。然而,这种模型对于许多开发者来说可…...

游戏遇到攻击有什么办法能解决?
随着网络技术的飞速发展,游戏行业在迎来繁荣的同时,也面临着日益严峻的网络威胁。黑客攻击、数据泄露、DDoS攻击等安全事件频发,给游戏服务器带来了极大的挑战。面对愈演愈烈的网络威胁,寻找一个能解决游戏行业攻击问题的安全解决…...
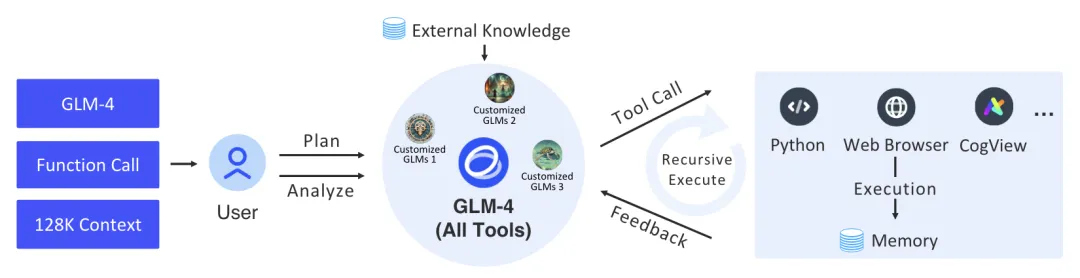
【LLM】GLM系列模型要点
note 文章目录 noteGLM一、数据层面1. 预训练数据 二、GLM4模型层面三、GLM-4 All Tools四、GLM的其他技术Reference GLM Paper:https://arxiv.org/abs/2406.12793 GitHub:https://github.com/THUDM HF:https://huggingface.co/THUDM 经过…...

安卓开发,获取本机手机号
用免费云服务器,三丰云记录安卓开发过程 以下是使用 Android 开发获取本机手机号的示例代码(需要相关权限): java 复制 import android.content.Context; import android.content.pm.PackageManager; import android.os.Build; i…...

linux学习week1
linux学习 一.介绍 1.概述 linux的读法不下10种 linux是一个开源的操作系统,操作系统包括mac、windows、安卓等 linux的开发版:Ubuntu(乌班图)、RedHat(红帽)、CentOS linux的应用:linux在服…...

【React篇】父组件渲染时避免重复渲染子组件的3种处理方法
在 React 中,父组件渲染时要避免重复渲染子组件,可以使用以下方法: 使用 React.memo(仅适用于函数式组件)或 PureComponent(适用于类组件): 这些方法可以帮助你创建在接收到新的 pr…...
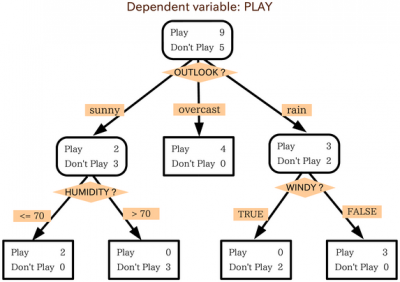
深度神经网络——决策树的实现与剪枝
概述 决策树 是一种有用的机器学习算法,用于回归和分类任务。 “决策树”这个名字来源于这样一个事实:算法不断地将数据集划分为越来越小的部分,直到数据被划分为单个实例,然后对实例进行分类。如果您要可视化算法的结果…...

IOPaint前后端框架
IOPaint 前后端框架 IOPaint 是一个图像修复工具,使用了先进的AI模型进行图像编辑。以下是其前后端所使用的框架: 前端框架 IOPaint 的前端使用了 Node.js 和 npm 进行依赖管理和构建。具体步骤如下: 克隆仓库并进入 web_app 目录&#x…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...