快速排序/快速选择算法
一.快速排序
1.基本介绍
快速排序(Quicksort〉是对冒泡排序的一种改进,都属于交换排序。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分(每次选择中轴值),中轴值左边的元素小于中轴值,中轴值右边的元素全部大于中轴值(但不要求有序),然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列

2.基本思路
我们每次选择一个中轴值,将中轴值和最后一个元素交换位置,对left到right-1的元素进行交换,当r<=l,此时l停留到的位置和right位置上的元素(中轴值)进行交换,这个时候,l停留的位置上是中轴值,并且左边的元素比中轴值小,右边的元素比中轴值大,然后递归对左边和右边的元素进行快速排序,直到left>=right的时候停止,此时数组便是有序的了.
1.关于中轴值的选择
大部分的可能给出的是选择第一个元素作为中轴值,但是这种做法有一定的弊端,如果是数组的元素是随机排序的,是可以接受的,但是如果数组的元素是预排序或者反序的,这样所有的元素不是全被划入到中轴值左边,就是划入到中轴值右边,那么时间复杂度就会很高
一种有效的方法时是采用随机产生一个下标为[left,right]的下标,这种情况下虽然可能会产生上面描述的情况,但总的来说可能性还是很小的.
还有一种方法是:三数中值分割法,我们选取三个数,使得三个数的最大值作为中轴值进行分割,一般来说我们选取左端,中端,右端的三个元素的终止作为中轴值,这种选取的方法还是
2.小数组情形
对于很小的数组(数组元素个数小于20),快速排序不如插入排序,因为快速排序是递归的.我们通常的做法是对于小的数组采用插入排序,一种好的截止范围是n=10,同时这种做法也避免了三数中值分割法的错误情况,比如最终数组的元素只有一个元素或者两个元素,而无法三数分割
3.时间复杂度
快速排序的平均时间复杂度:O(nlogn)
最好情况:O(nlogn)
最坏情况:O()
空间复杂度:O(logn)
同时快速排序不稳定,也就说元素相同的时候,原本在前边的元素,可能会最终被排序到后边
3.代码实现
1.随机值分割
public void quickSort(int[] nums, int left, int right) {if (left >= right)return;int index = (int) (left + Math.random() * (right - left + 1));int pivot = nums[index];//随机值生成indexswap(nums, index, right);int l = left, r = right - 1;while (true) {while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数l++;}while (r > 0 && nums[r] > pivot) {//r--;}if (l < r)swap(nums, l++, r--);elsebreak;}swap(nums, l, right);quickSort(nums, left, l - 1);quickSort(nums, l + 1, right);}
2.三数中值分割法
public static final int CUTOFF = 10;public int median(int[] nums, int left, int right) {int center = (left + right) / 2;if (nums[left] > nums[center])swap(nums, left, center);//此时center大于leftif (nums[left] > nums[right])swap(nums, left, right);//此时left为最小if (nums[center] > nums[right])swap(nums, center, right);//把center值放到right-1的位置swap(nums, center, right - 1);return nums[right - 1];}public void quickSort2(int[] nums, int left, int right) {//cutoff为截断值if (left + CUTOFF <= right) {int pivot = median(nums, left, right);//随机值生成indexint l = left+1, r = right - 2;while (true) {while (nums[l] < pivot) {//找到第一个比pivot大的数l++;}while (nums[r] > pivot) {//r--;}if (l < r)swap(nums, l++, r--);elsebreak;}swap(nums, l, right-1);quickSort2(nums, left, l - 1);quickSort2(nums, l + 1, right);} else {insertSort(nums, left, right);}}public void insertSort(int[] nums, int left, int right) {int j;for (int i = left; i <= right; ++i) {int temp = nums[i];//寻找插入的位置for (j = i; j > left && temp < nums[j - 1]; j--) {nums[j] = nums[j - 1];}nums[j] = temp;}}public void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}2.快速选择
1.基本介绍
快速选择算法其实是快速排序算法的变形,主要用于解决寻找第k大元素或者第k小元素,当我们需要寻找找到(排序后)第k个元素的时候,不要求数组的所有元素必须有序,这个时候我们可以选择使用快速选择算法,因为快速选择算法的时间复杂度比直接使用快速排序的时间复杂度低
快速选择的时间复杂度:O(n)
快速排序的时间复杂度:O(nlog(n))
①中轴值最终能交换到第k个位置,说明我们找到了第k个元素
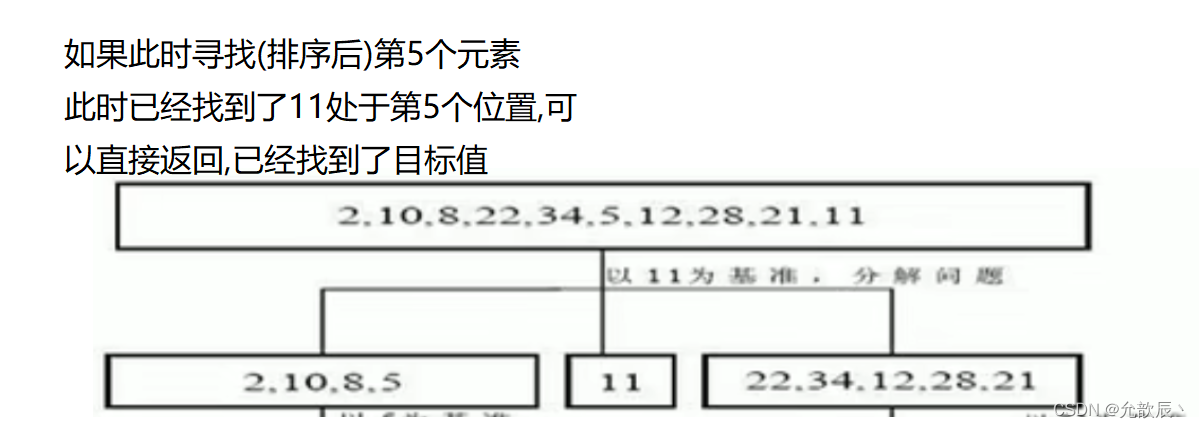
②中轴值最终的位置大于第k个位置,此时我们只需要对中轴值左边的元素进行快速排序
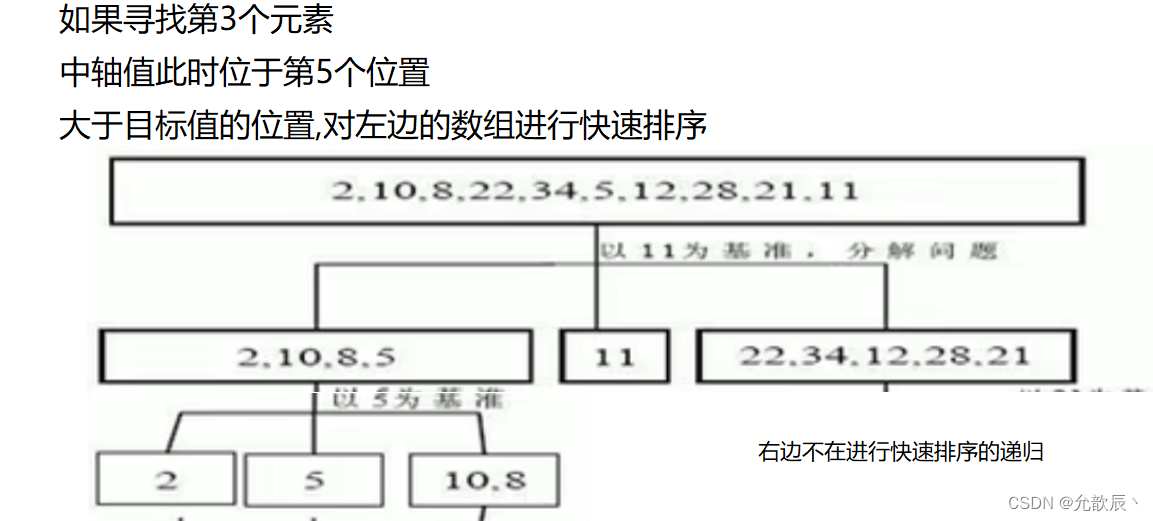
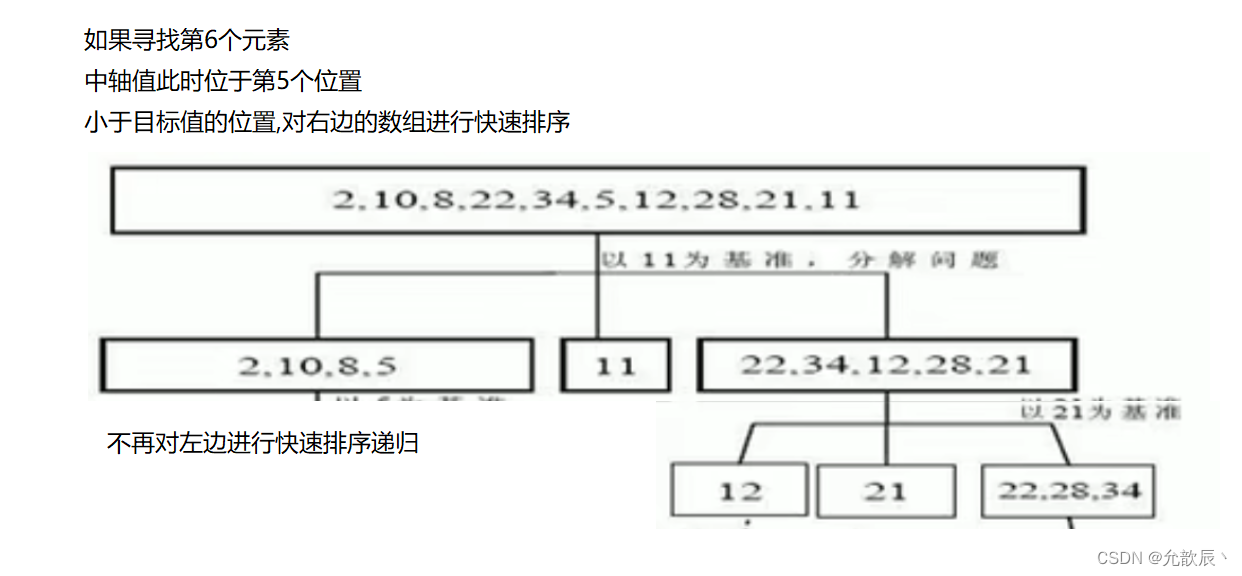
③中轴值最终的位置小于第k个位置,此时我们只需要对中轴值右边的元素进行快速排序
2.基本思路
快速选择的基本思路和快速排序算法还是一样的,无非就是多加了一个判断,判断是对中轴值左边进行快速排序,还是右边进行.
3.代码实现
1.随机值分割
public void quickSelect(int[] nums, int left, int right, int k) {if (left >= right)return;int index = (int) (left + Math.random() * (right - left + 1));int pivot = nums[index];//随机值生成indexswap(nums, index, right);int l = left, r = right - 1;while (true) {while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数l++;}while (r > 0 && nums[r] > pivot) {//r--;}if (l < r)swap(nums, l++, r--);elsebreak;}swap(nums, l, right);if (l > k) {quickSelect(nums, left, l - 1, k);} else if (l < k) {quickSelect(nums, l + 1, right, k);}}
2.三数中值分割法
public static final int CUTOFF = 10;public int median(int[] nums, int left, int right) {int center = (left + right) / 2;if (nums[left] > nums[center])swap(nums, left, center);//此时center大于leftif (nums[left] > nums[right])swap(nums, left, right);//此时left为最小if (nums[center] > nums[right])swap(nums, center, right);//把center值放到right-1的位置swap(nums, center, right - 1);return nums[right - 1];}public void quickSelect2(int[] nums, int left, int right, int k) {if (left + CUTOFF <= right) {int pivot = median(nums, left, right);int l = left + 1, r = right - 2;while (true) {while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数l++;}while (r > 0 && nums[r] > pivot) {//r--;}if (l < r)swap(nums, l++, r--);elsebreak;}swap(nums, l, right - 1);if (l > k) {quickSelect2(nums, left, l - 1, k);} else if (l < k) {quickSelect2(nums, l + 1, right, k);}} else {insertSort(nums, left, right);}}public void insertSort(int[] nums, int left, int right) {int j;for (int i = left; i <= right; ++i) {int temp = nums[i];//寻找插入的位置for (j = i; j > left && temp < nums[j - 1]; j--) {nums[j] = nums[j - 1];}nums[j] = temp;}}public void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}3.数组中的第K个最大元素
1.题目描述
给定整数数组
nums和整数k,请返回数组中第k个最大的元素。请注意,你需要找的是数组排序后的第
k个最大的元素,而不是第k个不同的元素。你必须设计并实现时间复杂度为
O(n)的算法解决此问题。
力扣:力扣
2.思路分析
看到题目我们就可以想到这一题可以使用快速选择算法肯定会更加高效,寻找第k个最大的元素,也就是寻找到nums.length-k个元素是什么即可,当然我们也可以直接快速排序,直接返回nums.length-k个元素
3.代码实现
1.直接使用快速排序
public int findKthLargest(int[] nums, int k) {quickSort(nums, 0, nums.length - 1);return nums[nums.length - k];}public void quickSort(int[] nums, int left, int right) {if (left >= right)return;int index = (int) (left + Math.random() * (right - left + 1));int pivot = nums[index];//随机值生成indexswap(nums, index, right);int l = left, r = right - 1;while (true) {while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数l++;}while (r > 0 && nums[r] > pivot) {//r--;}if (l < r)swap(nums, l++, r--);elsebreak;}swap(nums, l, right);quickSort(nums, left, l - 1);quickSort(nums, l + 1, right);}public void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}2.快速选择
public int findKthLargest(int[] nums, int k) {quickSelect(nums, 0, nums.length - 1,nums.length-k);return nums[nums.length - k];}public void quickSelect(int[] nums, int left, int right, int k) {if (left >= right)return;int index = (int) (left + Math.random() * (right - left + 1));int pivot = nums[index];//随机值生成indexswap(nums, index, right);int l = left, r = right - 1;while (true) {while (l < right && nums[l] < pivot) {//找到第一个比pivot大的数l++;}while (r > 0 && nums[r] > pivot) {//r--;}if (l < r)swap(nums, l++, r--);elsebreak;}swap(nums, l, right);if (l > k ) {quickSelect(nums, left, l - 1,k);} else if (l < k ) {quickSelect(nums, l + 1, right,k);}}public void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}4.数组中的第K个最大元素
1.题目描述
给你一个二维矩阵
matrix和一个整数k,矩阵大小为m x n由非负整数组成。矩阵中坐标
(a, b)的 值 可由对所有满足0 <= i <= a < m且0 <= j <= b < n的元素matrix[i][j](下标从 0 开始计数)执行异或运算得到。请你找出
matrix的所有坐标中第k大的值(k的值从 1 开始计数)。
力扣:力扣
2.思路分析
这一题首先需要解决的就是将所有坐标的异或运算的结果表达出来,然后用一个ArrayList存起来,然后这个时候我们就可以使用快速选择求出来第k大的值了.
首先我们需要解决的就是各个位置的异或结果的值,一想到异或,并且题目中明确表达出 满足0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j],这个时候我们可以想到使用异或前缀和进行解答,我们这个时候需要找到进行递推的异或表达式
借用力扣官方题解的一幅图片,我们可以看出来异或递推公式为
prefix[i][j] = prefix[i - 1][j] ^ prefix[i][j - 1] ^ prefix[i - 1][j - 1] ^ matrix[i - 1][j - 1];
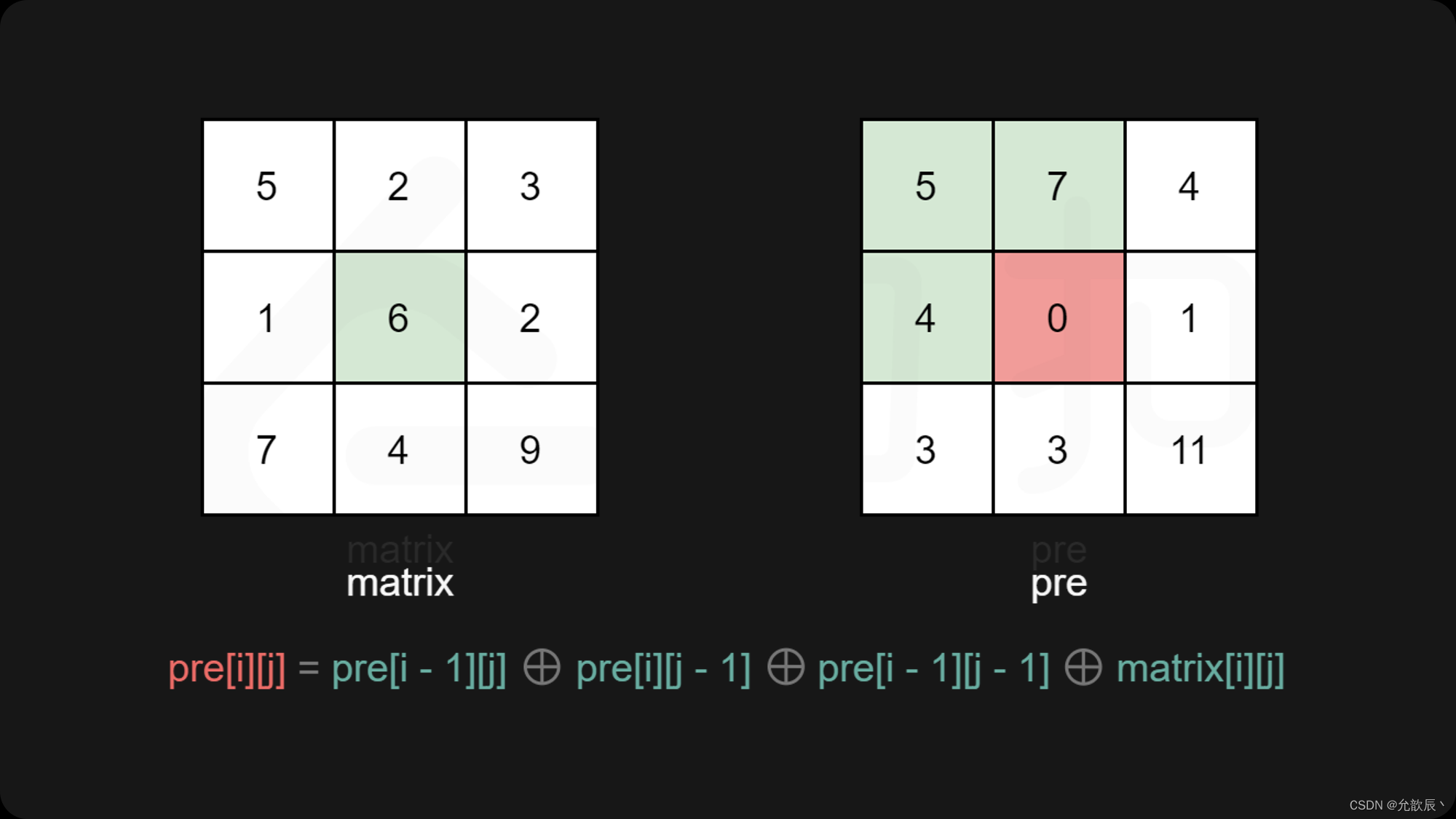
但我们我们看出(i,j)需要上一层的元素进行递推得到,如果我们定义的前缀异或的表达式长度为二维数组的大小的话,这个时候我们需要对第一行和第一列进行初始化,这个时候是很麻烦的,这个时候我们不妨定义的长度为m+1和n+1,刚开始元素的值都为1,并且一个值异或0还是本身,正好符合本题的意思
接下来进行快速选择,和上一题一样
3.代码实现
1.直接使用快速排序
public int kthLargestValue(int[][] matrix, int k) {int m = matrix.length;int n = matrix[0].length;int[][] prefix = new int[m + 1][n + 1];ArrayList<Integer> list = new ArrayList<>();for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {prefix[i][j] = prefix[i - 1][j] ^ prefix[i][j - 1] ^ prefix[i - 1][j - 1] ^ matrix[i-1][j-1];list.add(prefix[i][j]);}}quickSort(list, 0, list.size() - 1);return list.get(list.size() - k);}public void quickSort(List<Integer> list, int left, int right) {if (left >= right)return;int index = (int) (left + Math.random() * (right - left + 1));int pivot = list.get(index);//随机值生成indexswap(list, index, right);int l = left, r = right - 1;while (true) {while (l < right && list.get(l) < pivot) {//找到第一个比pivot大的数l++;}while (r > 0 && list.get(r) > pivot) {//r--;}if (l < r)swap(list, l++, r--);elsebreak;}swap(list, l, right);quickSort(list, left, l - 1);quickSort(list, l + 1, right);}public void swap(List<Integer> list, int i, int j) {int temp = list.get(i);list.set(i, list.get(j));list.set(j, temp);}2.快速选择
public int kthLargestValue(int[][] matrix, int k) {int m = matrix.length;int n = matrix[0].length;int[][] prefix = new int[m + 1][n + 1];ArrayList<Integer> list = new ArrayList<>();for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {prefix[i][j] = prefix[i - 1][j] ^ prefix[i][j - 1] ^ prefix[i - 1][j - 1] ^ matrix[i-1][j-1];list.add(prefix[i][j]);}}quickSelect(list, 0, list.size() - 1, list.size() - k);return list.get(list.size() - k);}public void quickSelect(List<Integer> list, int left, int right, int k) {if (left >= right)return;int index = (int) (left + Math.random() * (right - left + 1));int pivot = list.get(index);//随机值生成indexswap(list, index, right);int l = left, r = right - 1;while (true) {while (l < right && list.get(l) < pivot) {//找到第一个比pivot大的数l++;}while (r > 0 && list.get(r) > pivot) {//r--;}if (l < r)swap(list, l++, r--);elsebreak;}swap(list, l, right);if (l > k) {quickSelect(list, left, l - 1, k);} else if (l < k) {quickSelect(list, l + 1, right, k);}}public void swap(List<Integer> list, int i, int j) {int temp = list.get(i);list.set(i, list.get(j));list.set(j, temp);}相关文章:

快速排序/快速选择算法
一.快速排序 1.基本介绍 快速排序(Quicksort〉是对冒泡排序的一种改进,都属于交换排序。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分(每次选择中轴值),中轴值左边的元素小于中轴值,中轴值右边的元素全部大于中轴值(但不要求有序)&#x…...

【数据结构初阶】单链表面试题|内含链表带环问题
目录 前言 链表面试题 1. 删除链表中等于给定值 val 的所有节点。oj链接 2.反转一个单链表。oj链接 3. 给定一个带有头结点 head 的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个中间结点。oj链接 4. 输入一个链表,…...

一文解析ethtool 命令的使用
命令简介 ethtool命令用于查询和控制网络设备驱动程序和硬件设置,尤其是有线以太网设备,devname网卡的名称。网卡就像是交换机的一个端口,正常使用我们只是配置网卡IP地址等信息,网卡的速率、双工模式等我们并不关心。通过ethtoo…...
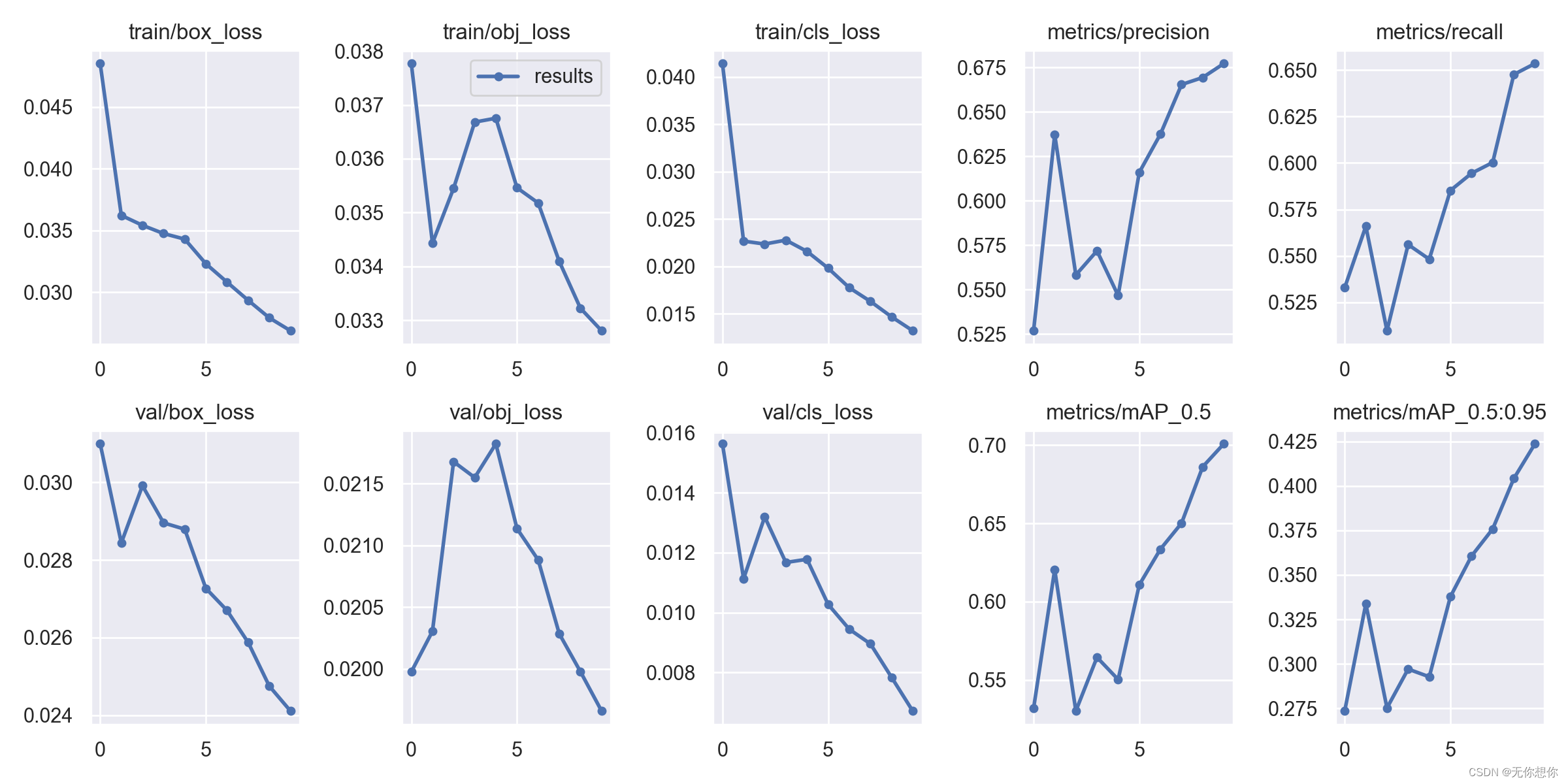
深度学习训练营之yolov5训练自己的数据集
深度学习训练营之训练自己的数据集原文链接环境介绍准备好数据集划分数据集运行voc_train.py遇到问题完整代码创建new_data.yaml文件模型训练时遇到的报错模型训练结果可视化参考链接原文链接 🍨 本文为🔗365天深度学习训练营 中的学习记录博客…...

Java中的AQS
文章目录什么是AQSAbstractQueuedSynchronizer方法解析自旋与阻塞ReentrantLock,Semaphore以及CountDownLatch对比ReentrantLock实现原理原理ReentrantLock源码中compareAndSetState的方法Semaphore实现原理CountDownLatch实现原理什么是AQS AQS是Java中的一个抽象…...

Spring——案例-业务层接口执行效率和AOP通知获取数据+AOP总结
执行时间获取:记录开始时间和结束时间,取差值。 这里使用环绕通知来实现。 环境准备: 项目文件结构: 业务层接口和实现类: 数据层: 采用mybatis注解开发,这里没有实现类,直接在接口方法里面实现映射。 domain层: 实现了数据库里面每一个…...

国外SEO舆情处理最佳黄金时间
在国外市场,SEO(搜索引擎优化)的舆情处理是非常重要的,因为它可以帮助提高网站的排名和流量,并且建立品牌的声誉和信誉。 然而,在什么时间进行舆情处理是一个值得探讨的问题。 在本文中,我们将…...
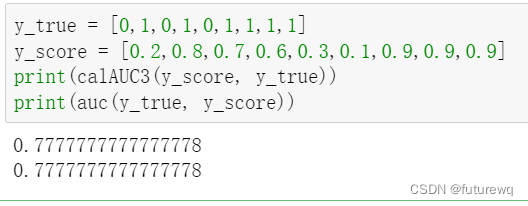
ROC和AUC
目录 ROC AUC ROC ROC曲线是Receiver Operating Characteristic Curve的简称,中文名为"受试者工作特征曲线"。ROC曲线的横坐标为假阳性率(False Postive Rate, FPR);纵坐标为真阳性率(True Positive Rate, TPR).FPR和TPR的计算方法分别为 F…...

Dopamine-PEG-cRGD,DOPA-PEG-cRGD,多巴胺-聚乙二醇-crgd细胞穿膜肽
名称:多巴胺-聚乙二醇-cRGD穿膜肽,多巴胺-聚乙二醇-crgd细胞穿膜肽英文名称:Dopamine-PEG-cRGD,DOPA-PEG-cRGD规格:50mg,100mg,150mg(根据要求可定制)描述:cRGD多肽序列: cyclo(RGDfK)外 观 : 半固体或固体,取决于分子量。溶解性:…...
动态规划回文子串
647. 回文子串方法:双指针回文子串有长度为奇数和偶数两种,extend(s, i, i, n); extend(s, i, i 1, n);就分别对应长度为奇数和偶数的情况class Solution { private:int extend(const string& s, int i, int j, int n) {int res 0;while (i > 0…...

windows 域控提权CVE-2014-6324CVE-2020-1472CVE-2021-42287CVE-2022-26923
一、CVE-2014-6324复现 环境:god.org域,两台主机,一台win2008域控,另一台web服务器win2008 工具:ms14-068.exe(漏洞exp) mimikatz psexec 利用条件: 1.域用户账号密码 2.获得一台主机权限(本地administ…...
1、JDK 安装 Java环境变量配置
jdk下载(Java8) (下载时间不同,小版本号会有变化,不影响后续安装) 官网下载地址:https://www.oracle.com/java/technologies/downloads/#java8-windows 下载完后安装 JDK 环境变量配置 Win…...
[c++]list模拟实现
目录 前言: 学习类的方式: 1 类成员变量 1.1 list成员变量 1.2 结点结构体变量 1.3 迭代器成员变量 2 默认函数——构造 2.1 结点结构体构造函数 2.2 list构造函数 2.3 迭代器构造函数 3 迭代器实现 3.1 list部分 3.2 迭代器结构体部分 3.2…...

实用的仓库管理软件有哪些,盘点2023年5大仓库管理软件!
对于做批发生意的老板或工厂老板来说,选择一款实用的仓库管理软件是至关重要的。仓库管理软件除了可以帮你降低仓库管理成本,提高经营管理的效率,还能够在手机上随时随地掌控仓库员工和商品的最新信息,与客户、供应商的订单情况能…...
透彻研究通过explain命令得到的SQL执行计划(1))
(八十二)透彻研究通过explain命令得到的SQL执行计划(1)
今天我们正式进入研究explain命令得到的SQL执行计划的内容了,只要把explain分析得到的SQL执行计划都研究透彻,完全能看懂,知道每个执行计划在底层是怎么执行的,那么后面学习SQL语句的调优就非常容易了。 首先,我们现在…...
【Linux】旋转锁 | 读写锁
在之前的线程学习中,用到的锁都是挂起等待锁,如果申请不到锁,那就会在锁中等待; 自旋锁则不大相似 文章目录1.自旋锁1.1 概念1.2 接口1.2.1 pthread_spin_init/destroy1.2.2 pthread_spin_lock1.2.3 pthread_spin_unlock2.读写锁…...
EasyExcell导出excel添加水印
EasyExcell导出excel添加水印1、添加easyExcel相关依赖2、准备基础工具类3、创建水印handler类4、创建单元测试类WriteTest.class5、测试结果1、添加easyExcel相关依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId&…...

SpringCloud:Nacos配置管理
Nacos除了可以做注册中心,同样可以做配置管理来使用。 1.1.统一配置管理 当微服务部署的实例越来越多,达到数十、数百时,逐个修改微服务配置就会让人抓狂,而且很容易出错。我们需要一种统一配置管理方案,可以集中管理…...
正则表达式引擎NFA自动机的回溯解决方案总结
前几天线上一个项目监控信息突然报告异常,上到机器上后查看相关资源的使用情况,发现 CPU 利用率将近 100%。通过 Java 自带的线程 Dump 工具,我们导出了出问题的堆栈信息。 我们可以看到所有的堆栈都指向了一个名为 validateUrl 的方法&#…...

卷积神经网络之AlexNet
目录概述AlexNet特点激活函数sigmoid激活函数ReLu激活函数数据增强层叠池化局部相应归一化DropoutAlexnet网络结构网络结构分析AlexNet各层参数及其数量模型框架形状结构关于数据集训练学习keras代码示例概述 由于受到计算机性能的影响,虽然LeNet在图像分类中取得了…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
