当前位置： 首页 > news >正文

apk反编译修改教程系列-----去除apk软件更新方法步骤列举 记录八种最常见的去除方法

news 2026/2/10 5:21:07

            在前面几期博文中 有说明去除apk软件更新的步骤方法。我们在对应软件反编译去除更新中要灵活运用。区别对待。同一个软件可以有不同的去除更新方法可以适用。今天的教程对于软件更新去除列举几种经常使用的修改步骤。

通过基础课程可以了解

1-----软件反编译更新去除的几种常用方式

2------app去更新的简单步骤描述

      软件更新弹窗有的可以跳过。有的必须点击更新才可以继续使用属于强制更新。那么经常使用的去除更新方法有以下几种

1-----最简单方法就是修改版本号【百分50的软件通用】

<

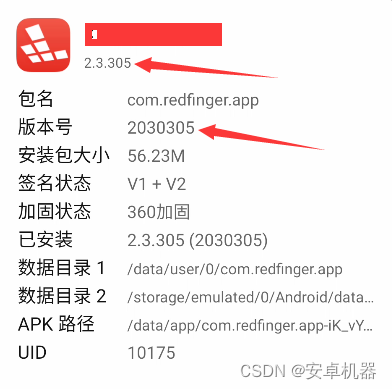
相关文章：

apk反编译修改教程系列-----去除apk软件更新方法步骤列举 记录八种最常见的去除方法

在前面几期博文中 有说明去除apk软件更新的步骤方法。我们在对应软件反编译去除更新中要灵活运用。区别对待。同一个软件可以有不同的去除更新方法可以适用。今天的教程对于软件更新去除列举几种经常使用的修改步骤。 通过基础课程可以了解 1-----软件反编译更新去除的几种常…...

编程日记 2024/6/25 15:34:44

SpringMVC系列六: 视图和视图解析器

视图和视图解析器 &#x1f49e;基本介绍&#x1f49e; 自定义视图为什么需要自定义视图自定义试图实例-代码实现自定义视图工作流程小结Debug源码默认视图解析器执行流程多个视图解析器执行流程 &#x1f49e;目标方法直接指定转发或重定向使用实例指定请求转发流程-Debug源码…...

编程日记 2024/6/25 15:31:38

MySQL数据备份的分类

MySQL数据库的备份 在我们使用MySQL数据库的过程中&#xff0c;一些意外情况的发生&#xff0c;有可能造成数据的损失。例如&#xff0c;意外的停电&#xff0c;不小心的操作失误等都可能造成数据的丢失。 所以为了保证数据的安全与一致性&#xff0c;需要定期对数据进行备份。…...

编程日记 2024/6/25 15:30:37

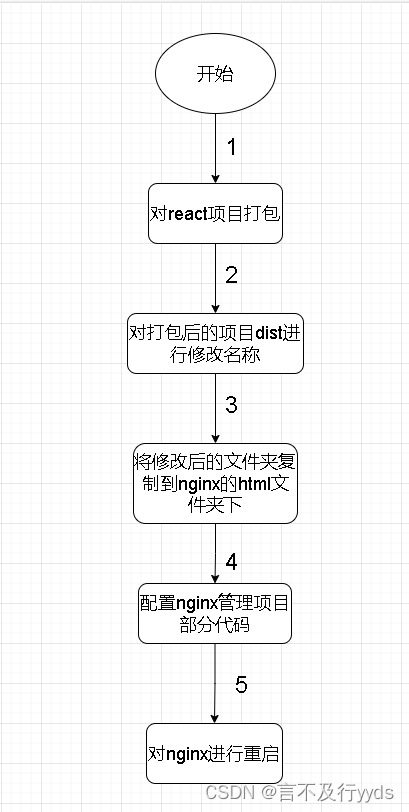
node+nginx实现对react进行一键打包部署--windows版

文章目录 nodenginx实现对react进行一键打包部署--windows版1.功能展示及项目准备1.1功能展示 1.2 项目准备1.2.1技术点1.2.2安装相关配置(windows) 2.实现2.1 实现思路2.2 实现步骤2.1 项目准备2.1.1 创建env文件2.1.2 创建api/index.js文件2.1.3 添加解决跨域代码 2.2 项目实…...

编程日记 2024/6/25 15:29:36

【机器学习】基于Gumbel-Sinkhorn网络的“潜在排列问题”求解

1. 引言 1.1.“潜在排列”问题 本文将深入探索一种特殊的神经网络方法，该方法在处理离散对象时展现出卓越的能力，尤其是针对潜在排列问题的解决方案。在现代机器学习和深度学习的领域中，处理离散数据一直是一个挑战，因为传统的神经网络架构通常是为连续数据设计的。然而，…...

编程日记 2024/6/25 15:27:33

create-react-app创建的项目中设置webpack配置

create-react-app 创建的项目默认使用的是 react-scripts&#xff08;存在于node_modules文件夹中&#xff09;来处理开发服务器和构建&#xff0c;它内置了一些webpack相关配置。一般不会暴露出来给开发者&#xff0c;但是在有些情况下我们需要修改下webpack默认配置&#xff…...

编程日记 2024/6/25 15:25:31

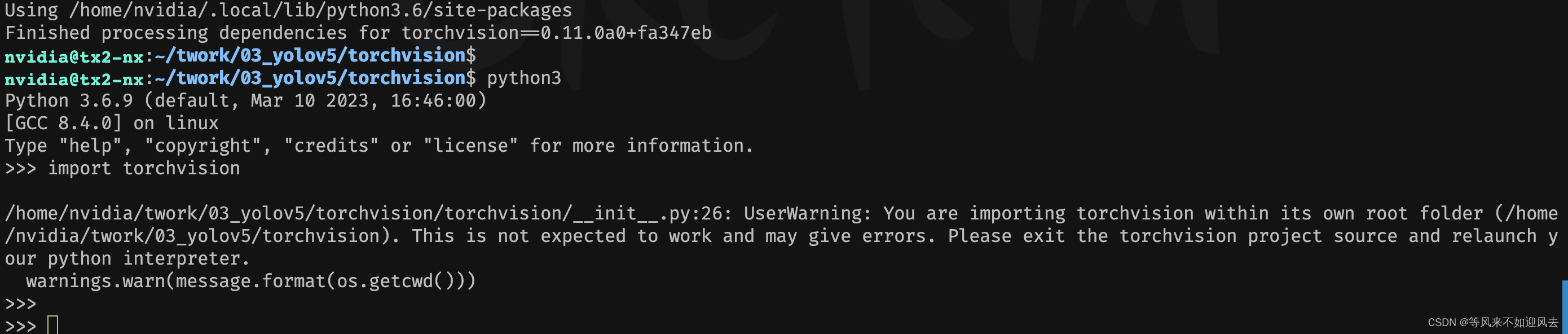
【ai】tx2 nx ：安装torch、torchvision for yolov5

torchvision 是自己本地构建的验证torchvision nvidia@tx2-nx:~/twork/03_yolov5/torchvision$ nvidia@tx2-nx:~/twork/03_yolov5/torchvision$ python3 Python 3.6.9 (default, Mar 10 2023, 16:46:00) [GCC 8.4.0] on linux Type "help", "copyright",…...

编程日记 2024/6/25 15:24:30

【报错】在终端中输入repo命令后系统未能识别这个命令

1 报错 已经使用curl命令来下载repo工具，但是在终端中输入repo命令后系统未能识别这个命令。 2 分析 通常是因为repo...

编程日记 2024/6/25 15:22:27

【机器学习】K-Means算法详解：从原理到实践

&#x1f308;个人主页: 鑫宝Code &#x1f525;热门专栏: 闲话杂谈&#xff5c; 炫酷HTML | JavaScript基础 ​&#x1f4ab;个人格言: "如无必要&#xff0c;勿增实体" 文章目录 K-Means算法详解&#xff1a;从原理到实践引言1. 基本原理1.1 簇与距离度量1.2 …...

编程日记 2024/6/25 15:20:24

解决qiankun项目与子应用样式混乱问题

背景 qiankun项目用的是Vue2Antdesign2&#xff0c;但其中一个子应用用的是Vue3Antdesign4。集成之后发现子应用的样式混乱&#xff0c;渲染的是Antdesign2的样式。 解决 以下步骤在子应用里操作 1. 在main.js引入ConfigProvider &#xff0c;在app全局注册ConfigProvider …...

编程日记 2024/6/25 15:19:23

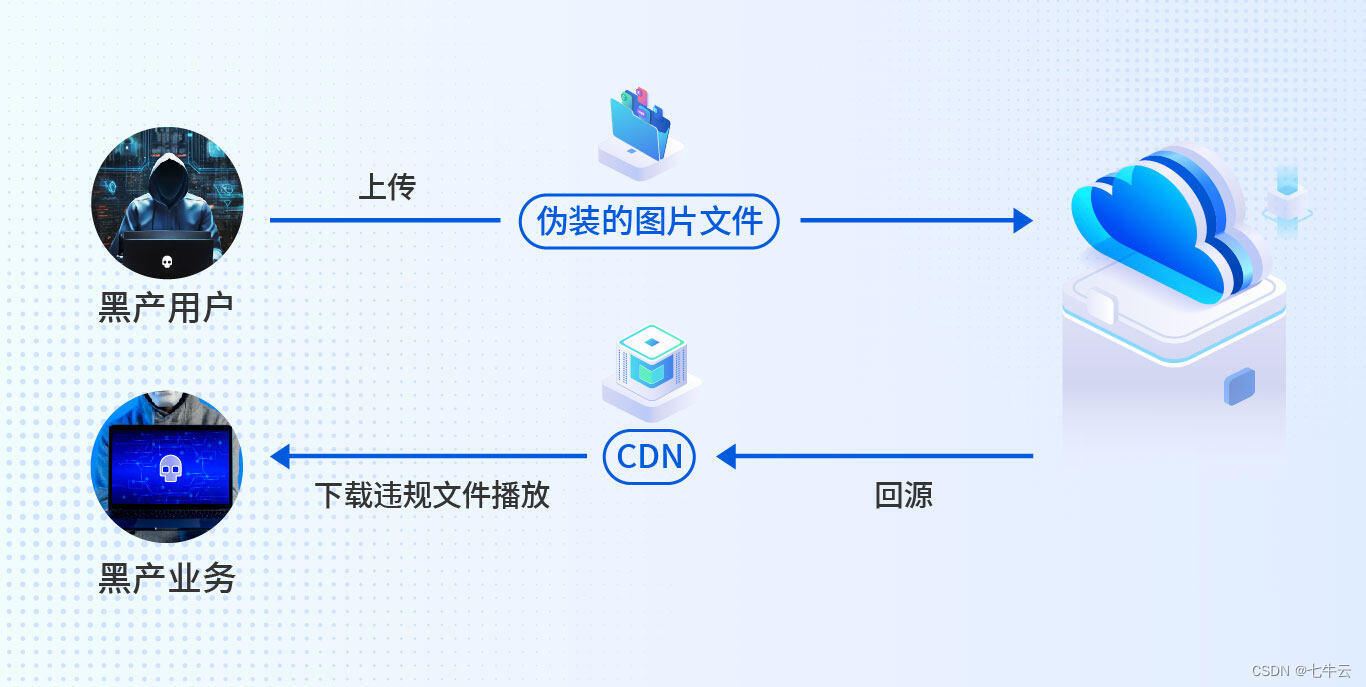
黑产当前，如何识别异常图片？

在这个人人都是创作者的年代&#xff0c; UGC 已成为诸多平台的重要组成。 有利益的地方就会有黑产存在&#xff0c; 不少 UGC 平台都被黑产「薅羊毛」搞的心烦意乱&#xff0c; 用户传的图片&#xff0c;怎么就变成视频链接了&#xff1f; 正常运营的平台&#xff0c;为何流量…...

编程日记 2024/6/25 15:18:21

数据模型(models)

自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 &#xff08;1&#xff09;在App中添加数据模型 在app1的models.py中添加如下代码&#xff1a; from django.db import models # 引入django.…...

编程日记 2024/6/25 15:14:15

【CS.AL】算法核心之贪心算法 —— 力扣(LeetCode)743. 网络延迟时间 - Dijkstra算法题解

文章目录 题目描述References 题目描述 743. 网络延迟时间 - 力扣&#xff08;LeetCode&#xff09; 有 N 个网络节点&#xff0c;标记为 1 到 N。 给定一个列表 times&#xff0c;其中 times[i] (u, v, w) 表示有一条从节点 u 到节点 v 的时延为 w 的有向边。 现在&#xf…...

编程日记 2024/6/25 15:13:14

25、架构-微服务的驱动力

微服务架构的驱动力可以从多方面探讨&#xff0c;包括灵活性、独立部署、技术异构性、团队效率和系统弹性等。 灵活性和可维护性 灵活性是微服务架构的一个主要优势。通过将单体应用拆分成多个独立的微服务&#xff0c;开发团队可以更容易地管理、维护和更新各个服务。每个微…...

编程日记 2024/6/25 15:11:12

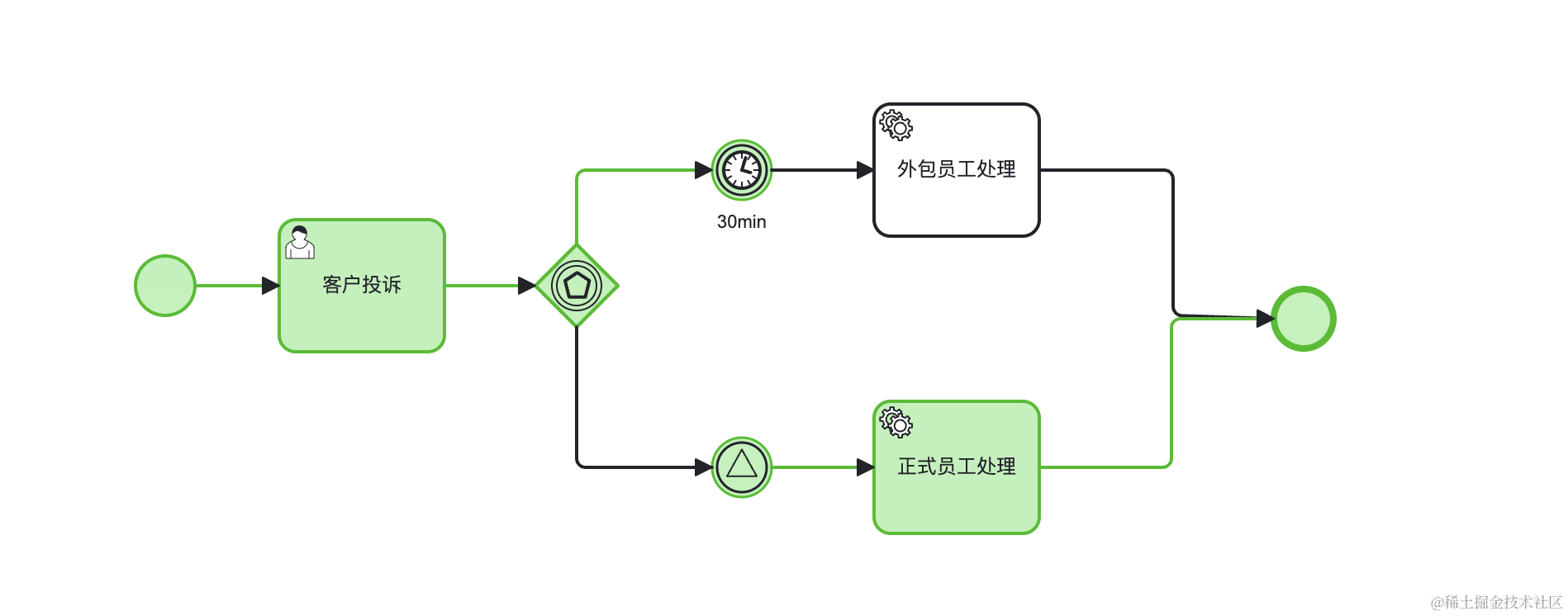
JeecgFlow事件网关概念及案例

事件网关 通常网关基于连线条件决定后续路径&#xff0c;但事件网关有所不同&#xff0c;其基于事件决定后续路径。事件网关的每条外出顺序流都需要连接一个捕获中间事件。 事件网关只有分支行为&#xff0c;流程的走向完全由中间事件决定。可以从多条候选分支中选择事件最先达…...

编程日记 2024/6/25 15:08:09

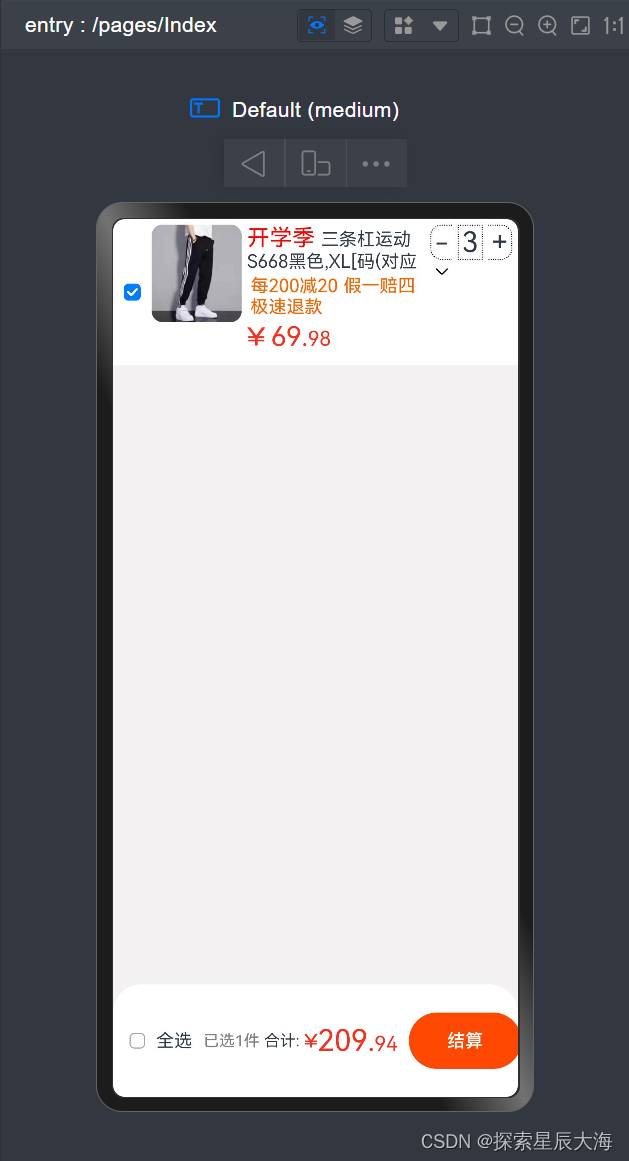
使用鸿蒙HarmonyOs NEXT 开发 快速开发 简单的购物车页面

目录 资源准备&#xff1a;需要准备三张照片&#xff1a;商品图、向下图标、金钱图标 1.显示效果&#xff1a; 2.源码&#xff1a; 资源准备&#xff1a;需要准备三张照片&#xff1a;商品图、向下图标、金钱图标 1.显示效果&#xff1a; 定义了一个购物车页面的布局&#x…...

编程日记 2024/6/25 15:07:06

iOS 中 attribute((constructor)) 修饰的函数

开发环境声明&#xff1a;此文描述的 attribute((constructor)) 特指使用 Objective-C 开发 iOS、MacOS&#xff0c;Swift 语言不支持这种属性修饰符。 初识 attribute((constructor)) 在 Objective-C 开发中&#xff0c;attribute((constructor)) 是一个 GCC 和 Clang 编译器…...

编程日记 2024/6/25 15:05:04

原生js实现图片预览控件，支持丝滑拖拽，滚轮放缩，放缩聚焦

手撸源代码如下&#xff1a;注释应该很详细了&#xff0c;拿去直用 可以放到在线编辑器测试&#xff0c;记得修改图片路径 菜鸟教程在线编辑器 <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" conten…...

编程日记 2024/6/25 15:03:02

C语言入门课程学习笔记9：指针

C语言入门课程学习笔记9 第41课 - 指针&#xff1a;一种特殊的变量实验-指针的使用小结 第42课 - 深入理解指针与地址实验-指针的类型实验实验小结 第43课 - 指针与数组&#xff08;上&#xff09;实验小结 第44课 - 指针与数组&#xff08;下&#xff09;实验实验小结 第45课 …...

编程日记 2024/6/25 15:02:00

借助 Cloudflare D1 和 Drizzle 在 Astro 上实现全栈

使用 Cloudflare D1 和 Drizzle ORM 将后端添加到 Astro 项目的分步指南 文章目录 安装 Astro添加 Cloudflare 适配器部署到 Pages安装 wrangler 并登录创建 D1 数据库创建 wrangler.toml 文件将 .wrangler 添加到 .gitignore更新 astro.config.ts安装 Drizzle 依赖项创建 driz…...

编程日记 2024/6/25 15:00:58

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能，多端兼容

基于 ​UniApp + WebSocket​实现多端兼容的实时通讯系统，涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能，适配​微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

编程新知 2026/1/22 16:15:42

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装

以下是基于 vant-ui&#xff08;适配 Vue2 版本 &#xff09;实现截图中照片上传预览、删除功能&#xff0c;并封装成可复用组件的完整代码&#xff0c;包含样式和逻辑实现&#xff0c;可直接在 Vue2 项目中使用&#xff1a; 1. 封装的图片上传组件 ImageUploader.vue <te…...

编程新知 2026/1/31 2:37:22

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序

一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

编程新知 2025/11/26 13:15:57

自然语言处理——Transformer

自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效&#xff0c;它能挖掘数据中的时序信息以及语义信息&#xff0c;但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN&#xff0c;但是…...

编程新知 2026/2/1 7:05:07

蓝桥杯 冶炼金属

原题目链接 &#x1f527; 冶炼金属转换率推测题解 &#x1f4dc; 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V&#xff0c;是一个正整数&#xff0c;表示每 V V V 个普通金属 O O O 可以冶炼出 …...

编程新知 2026/2/4 10:54:26

C#中的CLR属性、依赖属性与附加属性

CLR属性的主要特征 封装性&#xff1a; 隐藏字段的实现细节 提供对字段的受控访问 访问控制&#xff1a; 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性&#xff1a; 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑&#xff1a; 可以…...

编程新知 2025/12/4 0:13:33

MySQL JOIN 表过多的优化思路

当 MySQL 查询涉及大量表 JOIN 时&#xff0c;性能会显著下降。以下是优化思路和简易实现方法&#xff1a; 一、核心优化思路 减少 JOIN 数量 数据冗余&#xff1a;添加必要的冗余字段&#xff08;如订单表直接存储用户名&#xff09;合并表&#xff1a;将频繁关联的小表合并成…...

编程新知 2026/1/11 6:22:16

LabVIEW双光子成像系统技术

双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制&#xff0c;展现出显著的技术优势&#xff1a; 深层组织穿透能力&#xff1a;适用于活体组织深度成像 高分辨率观测性能&#xff1a;满足微观结构的精细研究需求 低光毒性特点&#xff1a;减少对样本的损伤…...

编程新知 2026/1/31 13:04:44

【无标题】湖北理元理律师事务所：债务优化中的生活保障与法律平衡之道

文/法律实务观察组 在债务重组领域&#xff0c;专业机构的核心价值不仅在于减轻债务数字&#xff0c;更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明&#xff0c;合法债务优化需同步实现三重平衡&#xff1a; 法律刚性&#xff08;债…...

编程新知 2026/1/31 9:00:14