【树状数组 队列】1505. 最多 K 次交换相邻数位后得到的最小整数
本文涉及知识点
树状数组 队列
LeetCode1505. 最多 K 次交换相邻数位后得到的最小整数
给你一个字符串 num 和一个整数 k 。其中,num 表示一个很大的整数,字符串中的每个字符依次对应整数上的各个 数位 。
你可以交换这个整数相邻数位的数字 最多 k 次。
请你返回你能得到的最小整数,并以字符串形式返回。
示例 1:
输入:num = “4321”, k = 4
输出:“1342”

解释:4321 通过 4 次交换相邻数位得到最小整数的步骤如上图所示。
示例 2:
输入:num = “100”, k = 1
输出:“010”
解释:输出可以包含前导 0 ,但输入保证不会有前导 0 。
示例 3:
输入:num = “36789”, k = 1000
输出:“36789”
解释:不需要做任何交换。
示例 4:
输入:num = “22”, k = 22
输出:“22”
示例 5:
输入:num = “9438957234785635408”, k = 23
输出:“0345989723478563548”
提示:
1 <= num.length <= 30000
num 只包含 数字 且不含有 前导 0 。
1 <= k <= 109
树状数组
第一种操作让s[i1]变小,第二种操作让s[i1+1…n-1]都变小。显然第一种操作比第二种操作更小。故i从小到大处理s[i]。
处理s[i]时,依次枚举下标最小的s[i]等于ch ,ch = ‘0’ to ‘9’ ,如果能交换则交换,并处理下一个i。
这样做的时间复杂度是:O(nn),超时。
令某字符的原始下标为i1,其它字符交换后若干次后i1的变化规律。如果起始位置都小于i1或都大于i1则对i1无影响。
由于从小到大处理i,所以起始位置i,一定小于i1。只需要统计大于i1的交换次数。如果原始下标大于i1的交换次数为cnt1,则i1当前的左边为i1+cnt1。 i1+cnt1需要交换i1+cnt1- i 次。下标大于i1的交换次数=总交换次数(i) - 下标小于等于i1的交换次数。
如果算上自己交换自己,交换一定能成功。
队列数组 indexs[i]升序记录 i+‘0’
交换成功的队列出队。
时间复杂度: O(nlogn)
代码
核心代码
template<class ELE = int >
class CTreeArr
{
public:CTreeArr(int iSize) :m_vData(iSize + 1){}void Add(int index, ELE value){index++;while (index < m_vData.size()){m_vData[index] += value;index += index & (-index);}}ELE Sum(int index){index++;ELE ret = 0;while (index){ret += m_vData[index];index -= index & (-index);}return ret;}ELE Get(int index){return Sum(index) - Sum(index - 1);}
private:vector<ELE> m_vData;
};class Solution {
public:string minInteger(string num, int k) {queue<int> indexs[10];for (int i = 0; i < num.length(); i++) {indexs[num[i] - '0'].emplace(i);}string ret;CTreeArr<int> ta(num.length());for (int i = 0; i < num.length(); i++) {for (int j = 0; j < 10; j++) {if (indexs[j].empty()) { continue; }const int inx = indexs[j].front();const int cnt1 = i - ta.Sum(inx);const int need = inx + cnt1 - i;if (need <= k) {k -= need;ta.Add(inx, 1);ret += ('0' + j);indexs[j].pop();break;}}}return ret;}
};
单元测试
template<class T1,class T2>
void AssertEx(const T1& t1, const T2& t2)
{Assert::AreEqual(t1 , t2);
}template<class T>
void AssertEx(const vector<T>& v1, const vector<T>& v2)
{Assert::AreEqual(v1.size(), v2.size()); for (int i = 0; i < v1.size(); i++){Assert::AreEqual(v1[i], v2[i]);}
}template<class T>
void AssertV2(vector<vector<T>> vv1, vector<vector<T>> vv2)
{sort(vv1.begin(), vv1.end());sort(vv2.begin(), vv2.end());Assert::AreEqual(vv1.size(), vv2.size());for (int i = 0; i < vv1.size(); i++){AssertEx(vv1[i], vv2[i]);}
}namespace UnitTest
{string num;int k;TEST_CLASS(UnitTest){public:TEST_METHOD(TestMethod0){num = "4321", k = 4;auto res = Solution().minInteger(num, k);AssertEx(string("1342"), res);}TEST_METHOD(TestMethod2){num = "100", k = 1;auto res = Solution().minInteger(num, k);AssertEx(string("010"), res);}TEST_METHOD(TestMethod3){num = "36789", k = 1000;auto res = Solution().minInteger(num, k);AssertEx(string("36789"), res);}TEST_METHOD(TestMethod4){num = "22", k = 22;auto res = Solution().minInteger(num, k);AssertEx(string("22"), res);}TEST_METHOD(TestMethod5){num = "294984148179", k = 11;auto res = Solution().minInteger(num, k);AssertEx(string("124498948179"), res);}};
}

扩展阅读
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关推荐
| 我想对大家说的话 |
|---|
| 《喜缺全书算法册》以原理、正确性证明、总结为主。 |
| 按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【树状数组 队列】1505. 最多 K 次交换相邻数位后得到的最小整数
本文涉及知识点 树状数组 队列 LeetCode1505. 最多 K 次交换相邻数位后得到的最小整数 给你一个字符串 num 和一个整数 k 。其中,num 表示一个很大的整数,字符串中的每个字符依次对应整数上的各个 数位 。 你可以交换这个整数相邻数位的数字 最多 k 次…...

【附精彩文章合辑】当谈到程序的“通用性”与“过度设计”的困境时,我们可以通过一些具体的例子来更直观地阐述这些解决方案
当谈到程序的“通用性”与“过度设计”的困境时,我们可以通过一些具体的例子来更直观地阐述这些解决方案。以下是一些示例: 一、明确需求与目标 例子1:在线购物平台 需求分析:平台需要支持用户注册、登录、浏览商品、下单购买、…...

Word中删除空白页
① 文字后面出现的空白页 把鼠标放在空白页的位置,按住Ctrl Delete即可。 ② 表格后面的空白页 把鼠标放在空白页左侧,直到出现一个空白的箭头,点击一下选中空白页,然后再Ctrl D,打开字体选项卡,在效果中…...

30.Netty进阶-黏包半包解决方案-短链接
客户端发送一次完整的消息,然后就把与服务端的链接断开。服务端读到的结果就是-1。 服务器就知道 从链接建立到断开,发送的数据是一条完整的数据。 客户端代码 package com.xkj.nian;import io.netty.bootstrap.Bootstrap; import io.netty.buffer.ByteBuf; import io.net…...
)
斜堆(数据结构篇)
数据结构之斜堆 斜堆 概念: 斜堆是左式堆的自调节形式,斜堆和左式堆间的关系类似于伸展树和AVL树间的关系斜堆是具有堆序性的二叉树,但是不存在对树的结构限制不同于左式堆,关于任意节点的零路径长的任何信息都不保留ÿ…...

河南大学24计算机考研数据,有三个学院招收计算机相关专业,都是考的408!
河南大学(Henan University),简称“河大”,是河南省人民政府与中华人民共和国教育部共建高校,国家“双一流”建设高校,入选国家“111计划”、中西部高校基础能力建设工程、卓越医生教育培养计划、卓越法律人…...

ubuntu离线安装docker导入镜像
docker安装包 准备工作 1.准备一个docker.service文件 内容如下: [Unit] DescriptionDocker Application Container Engine Documentationhttps://docs.docker.com Afternetwork-online.target firewalld.service Wantsnetwork-online.target[Service] Typenoti…...
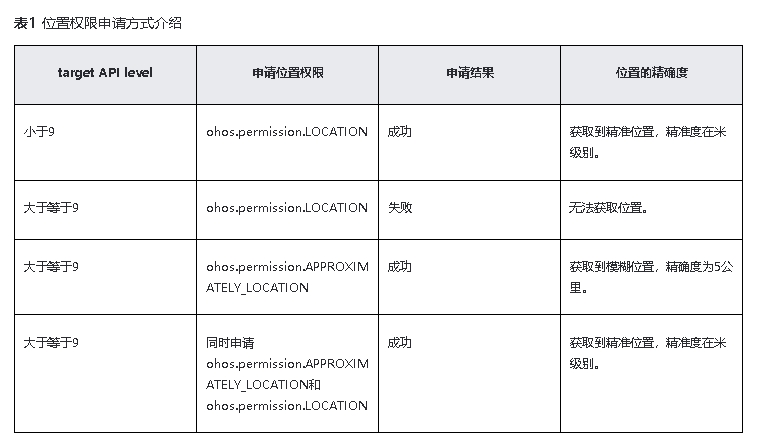
鸿蒙原生应用元服务开发-位置服务申请权限
申请位置权限开发指导 场景概述 应用在使用位置服务系统能力前,需要检查是否已经获取用户授权访问设备位置信息。如未获得授权,可以向用户申请需要的位置权限。 系统提供的定位权限有: ohos.permission.LOCATION:用于获取精准位置…...
基于SpringBoot的“智慧食堂”管理系统设计与实现
你好呀,我是计算机学姐码农小野!如果有相关需求,可以私信联系我。 开发语言:Java 数据库:MySQL 技术:SpringBootVue 工具:IDEA/Eclipse、Navicat、Maven 系统展示 首页 用户管理界面 菜品…...
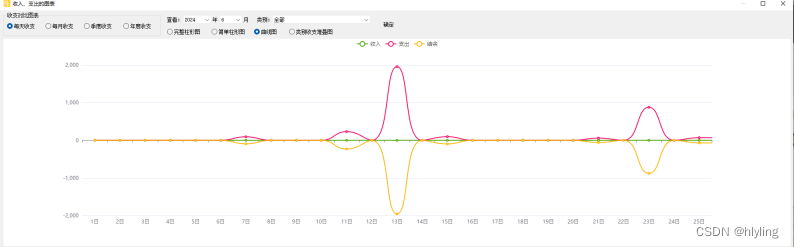
高效记录收支明细:揭秘如何通过曲线图精准分析每月开销
在理财的道路上,你是否曾感到迷茫和无力?每个月的开销如同流水般悄无声息地滑过指尖,但你却始终难以掌握自己的财务脉络。今天,我们为你揭秘一个全新的理财方法——通过曲线图精准分析每月开销,让你的财务生活焕发智慧…...

开发注意事项
开发注意事项 简介1. 查询条件照成的OOM问题原因注意事项 2. 因为事务导致数据查询不到问题原因注意事项 简介 这篇文章主要是想记录在开发过程中遇到的坑已经注意事项。 1. 查询条件照成的OOM 问题 SIT 环境内存突然暴增,直接打到100%,导致服务频繁…...

Vue79-路由组件独有的2个新的生命周期钩子
一、需求 news.vue路由组件被缓存了(因为想要保留里面的输入框的数据!),导致,路由页面切走,组件也不会被销毁,所以,beforeDestroy()函数就不会被执行,所以,定…...
Lua博客网站支持搜索、评论、登录注册
该简易博客示例用于学习网站的基础知识与MySQL数据库。 简述:开源Lua网站开发服务(FastWeb)支持:注册、登录、文章分页、评论分页、简易权限管理和搜索功能。发帖功能支持Markdown(支持记忆功能)图示:...

BGP高级特性
BGP路由反射器 l 路由反射器的两种角色 RR(router reflector):路由反射器 client:RR客户端 l RR会将学习到的路由反射出去,从而使得IBGP路由在AS内传播时无需建立IBGP的全互联结构 l 将一台BGP路由器指定为RR的…...

鸿蒙开发:1.环境搭建和入门
环境搭建 安装HUAWEI DevEco Studio 简介 HUAWEI DevEco Studio是基于IntelliJ IDEA Community开源版本打造, 为运行在HarmonyOS和OpenHarmony系统上的应用和服务提供一站式的开发平台。 特点 1.高效智能代码编辑:支持ArkTS、JS、C/C等语言的代码高亮、…...

python学习 - 设计模式 - 组合模式
组合模式 Composite , 将对象组组合成树形结构以表示’部分-整体’ 的层次结构.组合模式使得用户对单个对象的组合对象的使用具有一致性 #!/usr/bin/python # -*- coding:UTF-8 -*- # File : d1.py # Software: PyCharm""" 组合模式 Composite , 将对象组组…...

JavaScript倒序遍历数组:计算年度累积值
在 JavaScript 开发中,我们经常需要对数组中的数据进行特定顺序的处理。倒序 for 循环是一种常见的技术,它可以从数组的末尾开始向前遍历元素。这种技术特别适用于需要基于前一个元素的值来计算当前元素的场景。 示例场景:计算年度累积值 假…...

华为仓颉编程语言观感
这里写自定义目录标题 相似点(主要与Swift进行对比)不同点亮点 花了半天时间,对华为新出的仓颉编程语言做了简单的了解,整体观感如下: 仓颉语言看起来是一门大而全的语言,吸纳了现存的很多中编程语言的范式…...

Elasticsearch:倒数排序融合 - Reciprocal rank fusion - 8.14
警告:此功能处于技术预览阶段,可能会在未来版本中更改或删除。语法可能会在正式发布之前发生变化。Elastic 将努力修复任何问题,但技术预览中的功能不受官方正式发布功能的支持 SLA 约束。 倒数排序融合 (reciprocal rank fusion - RRF) 是一…...
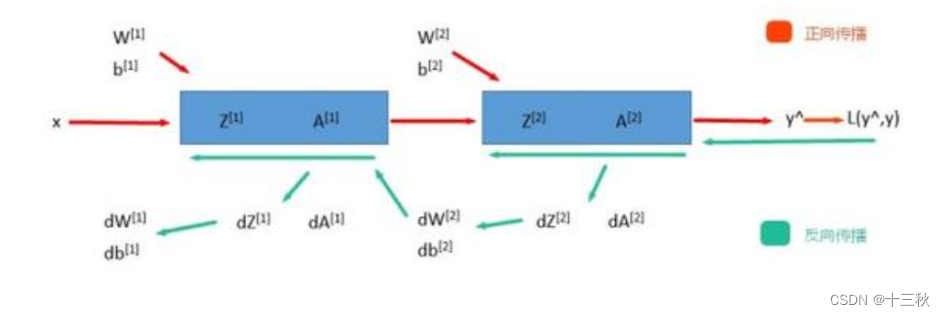
Day13—大语言模型
定义 大语言模型(Large Language Models)是一种基于深度学习的自然语言处理(NLP)模型,用于处理和生成人类语言文本。 一、认识NLP 什么是NLP NLP(Natural Language Processing)࿰…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
