MAB规范（3）：Chapter6 Glossary 术语表
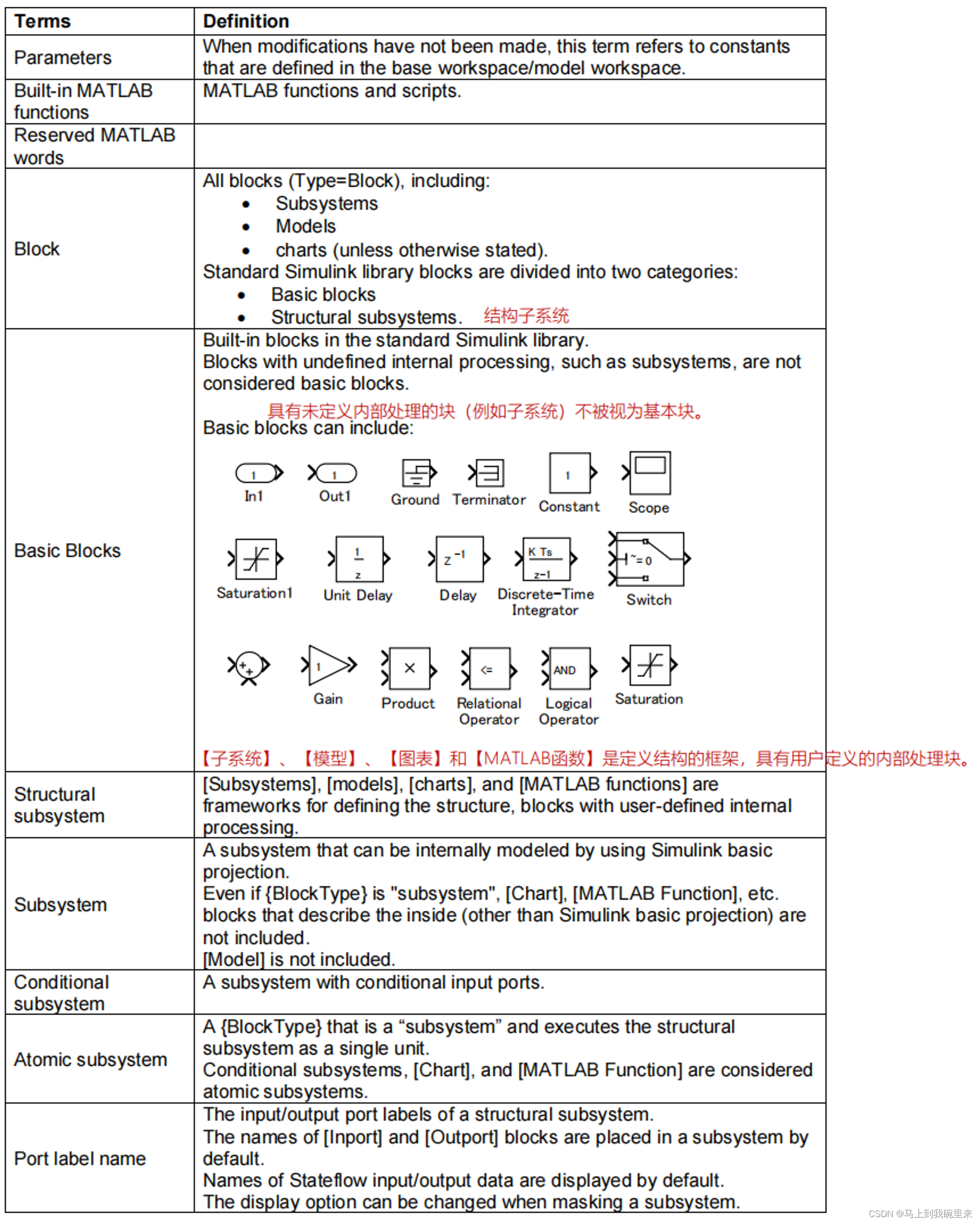
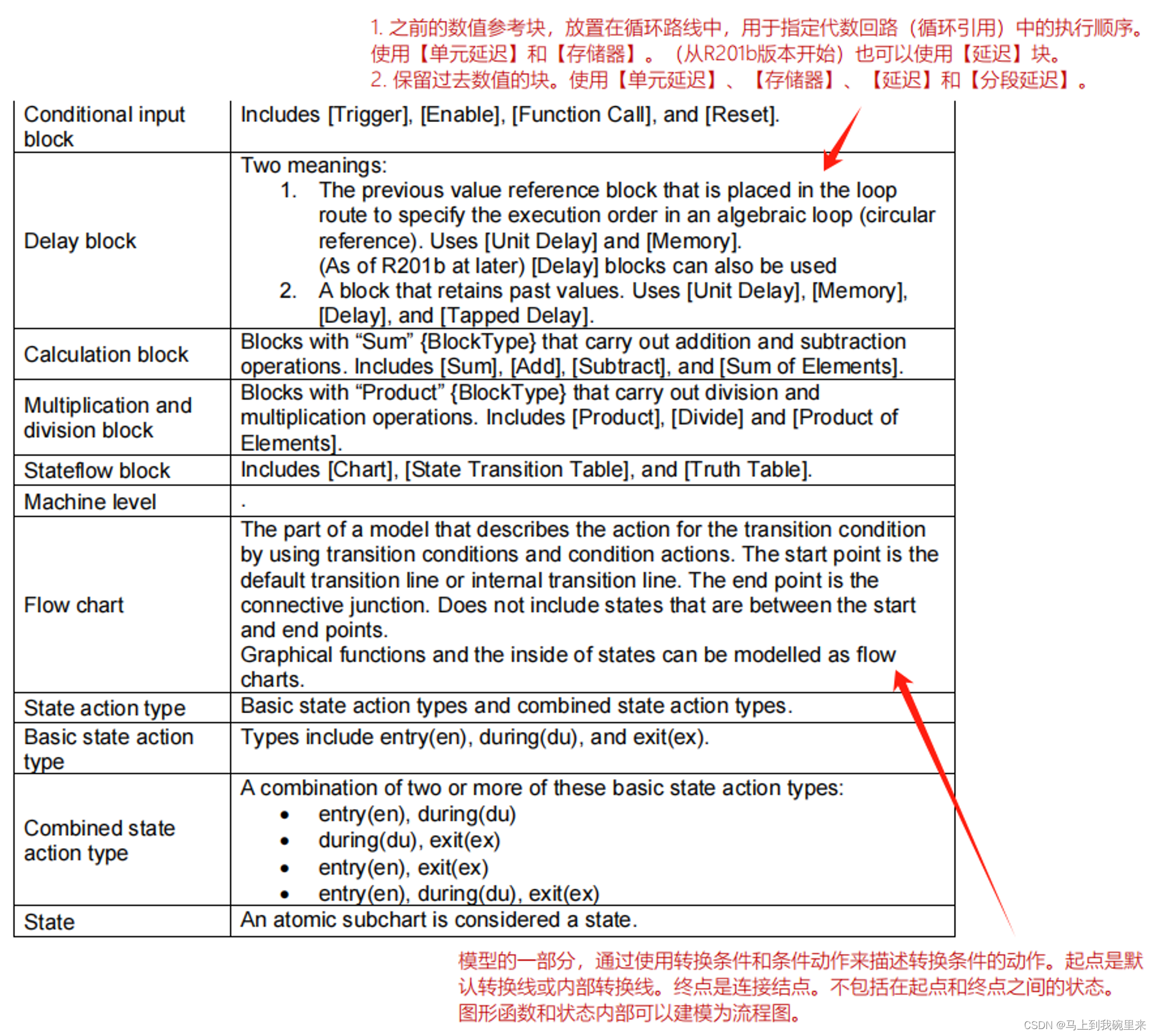
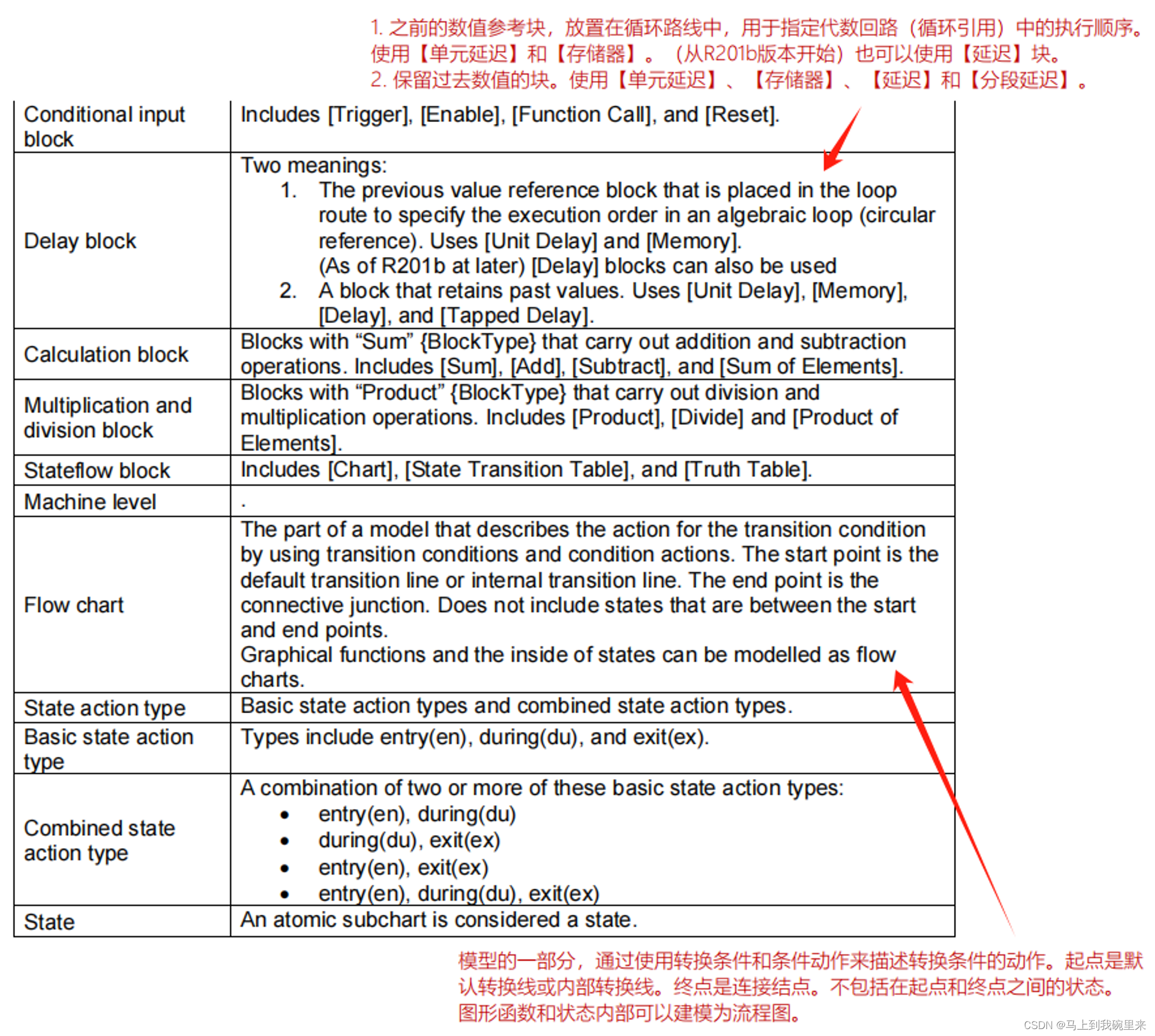
第6章 - 术语表
此章不做过多的批注，都是些简单的术语解释。
相关文章：
MAB规范（3）：Chapter6 Glossary 术语表
第6章 - 术语表 此章不做过多的批注，都是些简单的术语解释。...
40python数据分析numpy基础之diag处理矩阵对角线元素
1 python数据分析numpy基础之diag处理矩阵对角线元素 python的numpy库的diag(v,k0)函数，以一维数组的形式返回方阵的对角线元素，或将一维数组转换为方阵（非对角线元素为0）。 方阵：方形矩阵，行数和列数相等…...
ffmpeg+nginx+video实现rtsp流转hls流，web页面播放
项目场景： 最近调试海康摄像头需要将rtsp流在html页面播放,因为不想去折腾推拉流，所以我选择ffmpeg转hls流，nginx转发，html直接访问就好了 1.首先要下载nginx和ffmpeg 附上下载地址： nginx nginx news ffmpeg htt…...
1、Redis系列-Redis高性能原理详解
Redis高性能原理详解 Redis是一款高性能的内存数据库，广泛应用于需要快速读写访问的数据密集型应用中。它的高性能得益于多方面的设计和优化。以下是Redis高性能实现的详细解释： 1. 单线程架构 Redis采用单线程架构来处理客户端请求，这与传…...
18.枚举
学习知识：枚举类型、相关的使用方法 Main.java： public class Main {public static void main(String[] args) {myenum[] colorlist myenum.values();//获取枚举中所有对象的引用数组for (myenum one : colorlist){System.out.println(one.toString(…...
全省高等职业学校大数据技术专业建设暨专业质量监测研讨活动顺利开展
6月21日，省教育评估院在四川邮电职业技术学院组织开展全省高等职业学校大数据技术专业建设暨专业质量监测研讨活动。省教育评估院副院长赖长春，四川邮电职业技术学院党委副书记、校长冯远洪，四川邮电职业技术学院党委委员、副校长程德杰等出席…...
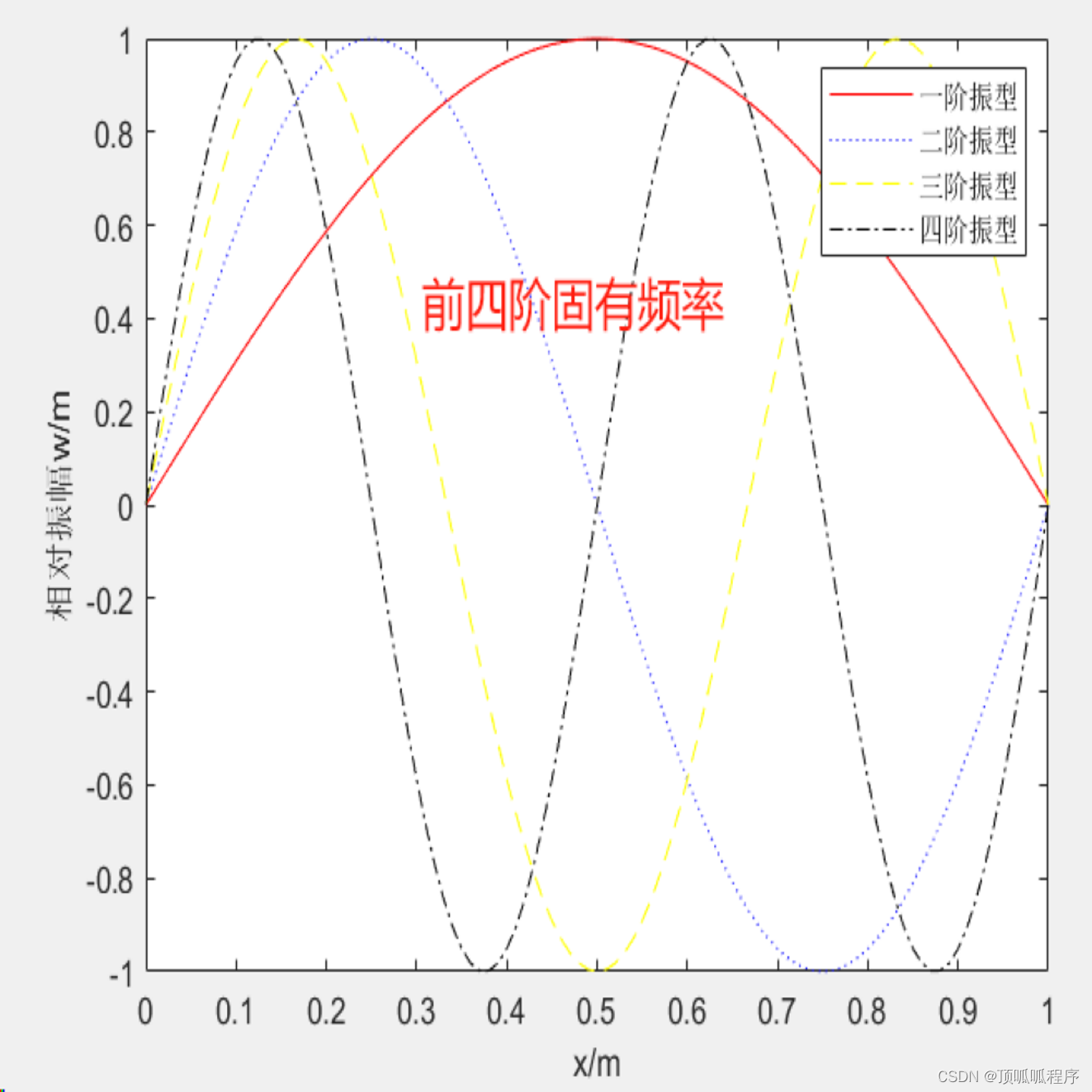
2-16 基于matlab的动载荷简支梁模态分析程序
基于matlab的动载荷简支梁模态分析程序，可调节简支梁参数，包括截面宽、截面高、梁长度、截面惯性矩、弹性模量、密度。输出前四阶固有频率，任意时刻、位置的响应结果。程序已调通，可直接运行。 2-16 matlab 动载荷简支梁模态分析 …...
AI大模型的核心
前言 没错，AI大模型的核心成功因素通常可以归结为三大要素：大数据、大算力和强算法。这三个因素相辅相成，共同推动了现代人工智能技术的发展。 1. 大数据 • 定义：指的是涵盖广泛领域的海量数据，包括文本、图像、音…...
【Android面试八股文】ViewHolder为什么要被声明成静态内部类？
文章目录 ViewHolder为什么要被声明成静态内部类？1. 避免隐式引用导致的内存泄漏2. 提高性能3. 代码可读性和维护性实例代码总结ViewHolder为什么要被声明成静态内部类？ 将 ViewHolder 声明为静态内部类有几个重要的原因，这样做可以提高性能并避免潜在的内存泄漏。下面是详…...
)
Android 11 系统OTA升级到旧版本(去除升级时间戳校验)
简介 由于客户要求能够通过OTA升级到旧版本因此探寻反向升级的方法。 方法一：进入recover模式 adb reboot recovery 点击Apply update from SD card 然后选择以前的OTA升级包就可以了。这种方式实测可以升级到旧的版本。但是我们的客户是通过在线升级软件进行更新…...
更新表的统计信息并清空缓存--DM8达梦数据库
更新表的统计信息并清空缓存--DM8达梦数据库 环境介绍1 收集 <表> 上所有对象信息，含索引2 清理缓存的执行计划3 达梦数据库学习使用列表 环境介绍 在某些环境刚完成数据迁移, 10万行以上大表数据量有修改1/3 ,查询条件已经创建索引,执行计划不好,或执行计划…...
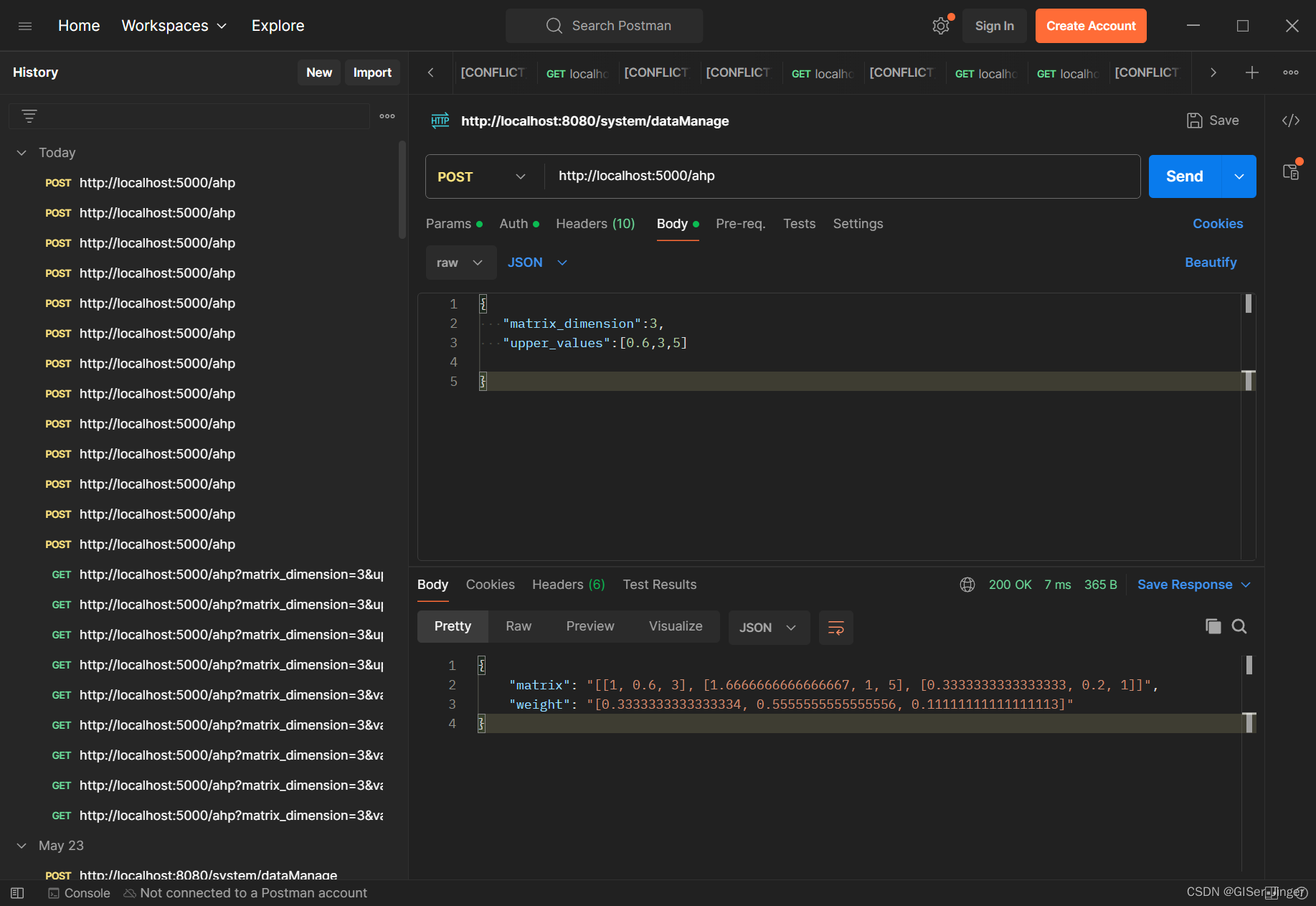
【前后端实现】AHP权重计算
AHP权重计算： 需求：前端记录矩阵维度、上三角值，后端构建比较矩阵、计算权重值并将结果返回给前端 比较矩阵构建 如果你想要根据上三角（不包括对角线）的值来构建对称矩阵，那么你可以稍作修改上述的generate…...
K8S日常运维手册
Kubernetes（简称 K8S）是一种广泛使用的容器编排平台，能够自动化部署、扩展和管理容器化应用。对于运维人员来说，掌握 Kubernetes 的日常运维技能是确保系统稳定运行的关键。本文将介绍一些 Kubernetes 日常运维的基本操作与技巧&a…...
现在的Java面试都这么扯淡了吗？
在开始前刚好我有一些资料，是我根据网友给的问题精心整理了一份「java的资料从专业入门到高级教程」， 点个关注在评论区回复“666”之后私信回复“666”，全部无偿共享给大家！！！开发兼过半年面试官 刚开始…...
安全加固 MariaDB 和 MySQL 数据库
安全加固 MariaDB 和 MySQL 数据库 在今天的网络环境中，保护数据库安全至关重要，特别是像 MariaDB 和 MySQL 这样的流行数据库。本文将介绍一些关键的安全加固步骤，以确保数据库系统的安全性和稳定性。 1. 数据库版本和基础设置 首先&…...
【计算机毕业设计】167校园失物招领微信小程序
🙊作者简介：拥有多年开发工作经验，分享技术代码帮助学生学习，独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件，帮助大学选题。赠送开题报告模板ÿ…...
yum的概念、相关命令、ftp http部署步骤；NFS共享文件操作步骤
目录 yum 配置文件 缓存功能操作步骤 创建并配置本地仓库文件 yum相关命令 yum install __ yum repolist yum list __ yum info __ yum search __ yum whatprovides __ yum remove __ yum -y update __ yum history yum grouplist yum groupinstall "__&q…...
Spire.PDF for .NET【文档操作】演示：如何删除 PDF 中的图层
借助Spire.PDF，我们可以在新建或现有pdf文档的任意页面中添加线条、图像、字符串、椭圆、矩形、饼图等多种图层。同时，它还支持我们从pdf文档中删除特定图层。 Spire.PDF for .NET 是一款独立 PDF 控件，用于 .NET 程序中创建、编辑和操作 PD…...
【c语言】二级指针
1，定义 本质还是从指针的角度去理解，只不过存的指针的值 2，使用方法...
心理健康测试系统设计
心理健康测试系统设计需要综合考虑多个方面，以确保系统的准确性、易用性和有效性。以下是一个心理健康测试系统设计方案： 一、设计目标 准确性：确保测试结果能够准确反映被测者的心理健康状况。 易用性：设计简洁明了的界面和操作…...
论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）
HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...
Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
多模态商品数据接口：融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 （一）多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如，当用户上传一张“蓝色连衣裙”的图片时，接口可自动提取图像中的颜色（RGB值&…...
el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现，这取决于你是想在组件内部直接设置，还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法： 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
ESP32 I2S音频总线学习笔记（四）： INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入，一个是通过INMP441麦克风模块采集音频，一个是通过PCM5102A模块播放音频，那如果我们将两者结合起来，将麦克风采集到的音频通过PCM5102A播放，是不是就可以做一个扩音器了呢…...
Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统，支持多语言对话（如 中文，英文，日语），语音情感（如 开心，悲伤）&#x…...
【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令，在Linux上安装软件，以及如何在Linux上部署一个单体项目，大多数同学都会有相同的感受，那就是麻烦。 核心体现在三点： 命令太多了，记不住 软件安装包名字复杂&…...
QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体（对象或容器）QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质（定义颜色、反光等）QFirstPersonC…...
云原生安全实战：API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填！ 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关（API Gateway） API网关是微服务架构中的核心组件，负责统一管理所有API的流量入口。它像一座…...