算法设计与分析 笔记
截图摘自湖南大学彭鹏老师的ppt。笔记也是根据他的ppt整理的。
动态规划
核心
用数组记录中间结果,避免重复计算
三角数塔问题
问题描述
给定一个三角形数塔,从顶部出发,每次只能移动到下一行的相邻元素。要求找到一条路径,使得路径上的数字和最大。
假设有一个三角形数塔,如下所示:
37 42 4 68 5 9 3
dp数组 dp[i][j]表示以matrix[i][j]为结尾的,最大路径的和
310 712 14 1320 19 23 16
最后结果是23
解题思路
dp[i][j]=max(dp[i-1][j],dp[i-1][j+1])+matrix[i][j];
伪代码
int max_value(vector<vector<int>> &matrix ){vector<vector<int>> dp(matrix.size(),vector<int>(matrix.size()));dp[0][0] = matrix[0][0];for(int i=1;i<matrix.size();i++){dp[i][0] = dp[i-1][0] + matrix[i][0]; // 最左边的for(int j=1;j<i;j++){// 中间的dp[i][j] = max(dp[i-1][j-1],dp[i-1][j]) + matrix[i][j];}// 最右边的dp[i][i] = dp[i-1][i-1] + matrix[i][i];}return max(dp.back().begin(),dp.back().end());
};复杂度分析
时间复杂度:O(n^2),其中 n 是三角形的行数。
空间复杂度:O(n^2),其中 n 是三角形的行数。
最大字段和
问题描述
给定由n个整数(可能有负整数)组成的序列(a1, a2, …, an),最大子段和问题要求该序列形如 的最大值(1≤i≤j≤n),当序列中所有整数均为负整数时,其最大子段和为0。
示例
例如,序列(-20,11,-4,13, -5, -2)的最大子段和为 a2+a3+a4=20 。
dp[i]表示以a[i]开头的,从a[i]–>a.back()的最大子段和
dp数组
dp[i] = max(dp[i+1]+a[i],a[i]);
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| a | -20 | 11 | -4 | 13 | -5 | -2 |
| dp | 0 | 20 | 9 | 13 | -5 | -2 |
所以最后答案是20
// 注意是后序
int max_sub_array(vector<int> &a){int n = a.size();vector<int> dp(n);dp.back() = a.back();int max_sum = a[0];for(int i=n-2;i>=0;i--){dp[i] = max(dp[i+1]+a[i],a[i]);max_sum = max(max_sum,dp[i]);}return max_sum;
}
复杂度分析
时间复杂度:O(n),其中 n 是序列的长度。
空间复杂度:O(n),其中 n 是序列的长度。
最长公共子序列
问题描述
给定两个字符串str1和str2,返回两个字符串的最长公共子序列(LCS)。
子序列是指从原字符串中删除若干个字符后,不改变剩余字符顺序得到的字符串。最长公共子序列是两个字符串所共同拥有的最长子序列。
例如,对于字符串"abcde"和"ace",最长公共子序列是"ace",因此长度为3。
示例
abcbdab
bdcaba
dp[i][j]表示str1[0:i]和str2[0:j]的最长公共子序列长度
| start | a | b | c | b | d | a | b | |
|---|---|---|---|---|---|---|---|---|
| start | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| b | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| d | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 |
| c | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 |
| a | 0 | 1 | 1 | 2 | 2 | 2 | 3 | 3 |
| b | 0 | 1 | 2 | 2 | 3 | 3 | 3 | 4 |
| a | 0 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
所以最后答案是4 bdab
代码
int longest_common_subsequence(string &str1,string &str2){int n = str1.size();int m = str2.size();vector<vector<int>> dp(n+1,vector<int>(m+1,0));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(str1[i-1] == str2[j-1]){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = max(dp[i-1][j],dp[i][j-1]);}}}return dp[n][m];
}
复杂度分析
时间复杂度:O(nm),其中 n 和 m 分别是字符串 str1 和 str2 的长度。
空间复杂度:O(nm),其中 n 和 m 分别是字符串 str1 和 str2 的长度。
01背包问题
问题描述
给定 n 种物品和一个容量为 w 的背包,每种物品都只有一件可用。第 i 种物品的体积是 vi,价值是 wi。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
示例
number=4 capacity=8
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| s (weight) | 2 | 3 | 4 | 5 |
| v (value) | 3 | 4 | 5 | 6 |
dp数组
dp[i][j]表示,在总容量为j的情况下,在0~i个物品中,能获得的最大价值。
dp[i][j]=max(dp[i-1][j],dp[i-1][j-s[i]]+v[i])
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 2 | 0 | 0 | 3 | 4 | 4 | 7 | 7 | 7 | 7 |
| 3 | 0 | 0 | 3 | 4 | 4 | 7 | 8 | 9 | 9 |
| 4 | 0 | 0 | 3 | 4 | 4 | 7 | 8 | 9 | 10 |
代码
int max_value_in_knapsack(vector<int> &s,vector<int> &v,int capacity){int n = s.size();vector<vector<int>> dp(n+1,vector<int>(capacity+1,0));for(int i=1;i<=n;i++){for(int j=1;j<=capacity;j++){if(j>=s[i-1]){dp[i][j] = max(dp[i-1][j],dp[i-1][j-s[i-1]]+v[i-1]);}else{dp[i][j] = dp[i-1][j];}}}return dp[n][capacity];
}
复杂度分析
时间复杂度:O(nm),其中 n 和 m 分别是物品的数量和背包容积。
空间复杂度:O(nm),其中 n 和 m 分别是物品的数量和背包容积。
贪心算法
选取局部最优解
优缺点
- 优点:速度快,复杂度低
- 缺点:需要证明是最优解
活动选择问题
问题描述
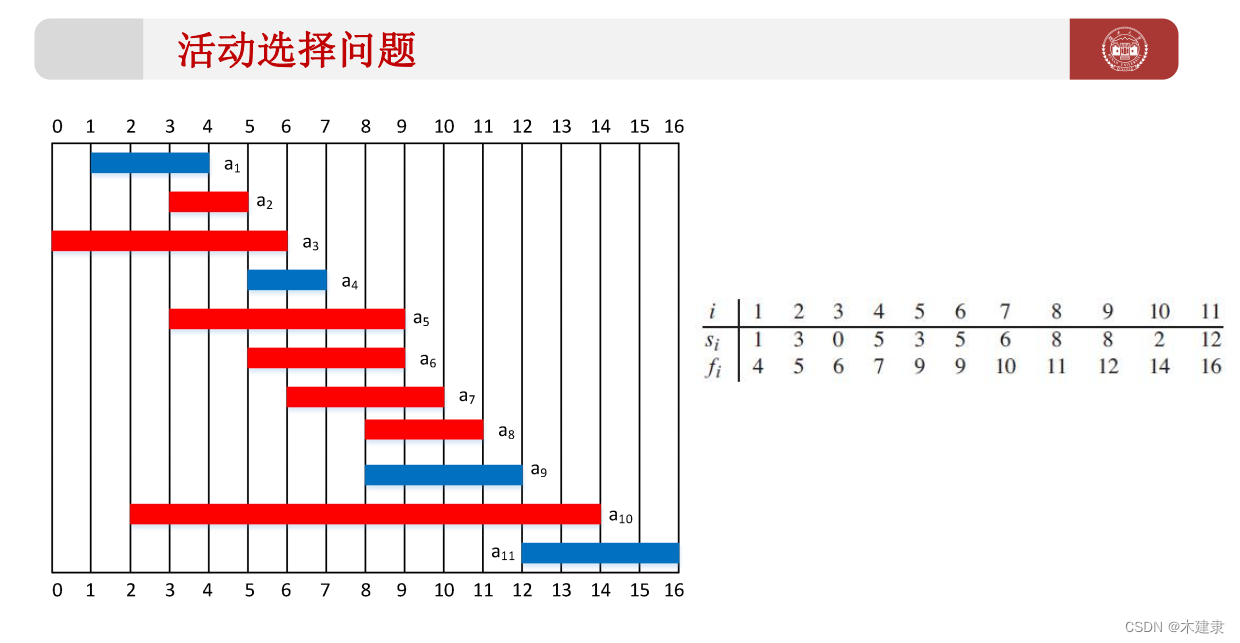
假设我们存在这样一个活动集合S={a1,a2,a3,a4,…,an},其中每一个活动ai都有一个开始时间si和结束时间fi保证(0≤si<fi),活动ai进行时,那么它占用的时间为[si,fi),现在这些活动占用一个共同的资源(教室),就是这些活动会在某一时间段里面进行安排,如果两个活动ai和aj的占用时间[si,fi),[sj,fj)不重叠,那么就说明这两个活动是兼容的,也就是说当sj>=fi或者si>=fj那么活动ai,aj是兼容的。在活动选择问题中,我们希望选出一个最大兼容活动集,即在同一间教室能安排数量最多的活动。
贪心策略
按照结束时间前的,放前面;结束时间一样的,开始时间小的放前面,然后依次相加
贪心证明
贪心的结果集是S, 剩下的集合是T,对于T中的任意一个元素b,都存在一个a属于S, 是a的结束时间大于b的开始时间。
代码
static bool cmp (const vector<int>&a, const vector<int>&b){return a[1]<b[1];}
int eraseOverlapIntervals(vector<vector<int>>& vct) {sort(vct.begin(),vct.end(),cmp);int endtime=vct.front()[1];int res=1;for(int i=1;i<vct.size();i++){if(endtime > vct[i][0]){}else{endtime=vct[i][1];res++;}}return res;}
建议
碰到这种问题,用动态规划也能做,而且如果对应的活动有权值,动态规划还一定是正确的。
- 对任务按照结束时间排序
- dp[i][j] i表示从0~i个任务,j表示空余时间,dp[i][j]表示最大解
哈夫曼编码
问题描述
给定一个由n个不同字符组成的字符串,请设计一个哈夫曼编码,使得使用该编码的编码长度最小。
哈夫曼树
- 定义:给定n个权值作为n个叶子结点的权值,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
解法
- 统计待编码字符串中每个字符出现的次数,并将这些次数作为权重存储在数组中。
- 根据权重构建哈夫曼树。在构建过程中,每次从权重数组中取出两个最小的权重,将它们合并为一个新节点,新节点的权重为这两个节点权重之和。然后将新节点加入哈夫曼树,同时从权重数组中删除这两个节点。重复这个过程,直到权重数组为空。
- 根据哈夫曼树生成哈夫曼编码。对于哈夫曼树的每个叶子节点,从根节点到叶子节点的路径上的每个节点对应一个0或1,将这些0和1按照从根节点到叶子节点的顺序连接起来,就得到了该叶子节点的哈夫曼编码。
- 使用哈夫曼编码对字符串进行编码。将字符串中的每个字符替换为其哈夫曼编码,然后将编码后的字符串按照哈夫曼编码的规则进行传输或存储。
最小延迟调度问题
问题描述
任务集合S,∀i∈S,di 为截止时间,ti为加工时间,di , ti为正整数。一个调度f : S→N,f(i)为任务i 的开始时间。求最大延迟达到最小的调度,就是所有任务超过截止时间的和最小。

解决方案
按照结束时间di从小到大排序,安排时不留空余时间
贪心证明
最优解中可以不存在相邻的逆序任务,使得(i,j): f(i) < f(j) di > dj。 (真确解中,交换两个任意的任务,都会使得总任务拖延时间变长)。
找零问题
问题描述
考虑用最少的硬币找n美分零钱的问题。假设每种硬币的面额都是整数。设计贪心算法求解找零问题,假定有25美分、10美分、5美分和1美分4种面额的硬币。证明你的算法能找到最优解。
解决方案
按照先尽可能用25美分,然后尽可能用10美分,再尽可能用5美分,最后尽可能用1美分。
贪心证明
假设一个可能的解中,存在两个10,一个5,则可以用25代替,获取到一个更优解。同样递归,直到没有硬币组合能到25,对应着先用25美分的。
图基本算法
广度优先搜索
算法步骤
广度优先搜索(BFS,Breadth First Search),从初始点开始,逐层向前搜索,即第n层搜索未完成,不得进入下一层搜索。
深度优先搜索
算法步骤
深度优先搜索(DFS,Depth First Search),从初始点开始,对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次
欧拉回路
判定条件
对于图上的任意节点,入度等于出度。
DFS解法
- 从任意一个起始点v开始DFS遍历,直到再次到达点v,即寻找一个回路。
- 将此回路定义为C,如果回路C中存在某个点x,其有出边不在回路中,则继续以此点x开始遍历寻找回路C’,将环C、C’连接起来也是一个大回路,如此往复,直到图G中所有的边均已经添加到回路中
- 显然每条边只会返回一次,所以复杂度为O(E)
用人话说就是:
- 对任意一个节点A做DFS, 直到终点到了A,对遍历的边进行标记,把所有遍历的边去除。
- 对任意一个还有边的点B进行DFS,重复操作,直到所有边都被标记。
- 标记的边就是欧拉回路。
拓扑排序
算法步骤
- 找到所有入度为0的节点,并加入队列
- 依次从队列中取出节点,并将其指向的节点的入度减1,如果减1后,该节点的入度为0,则将其加入队列
最小生成树
把所有点都连接起来,使得生成树各边权值之和最小。
prim算法
算法步骤
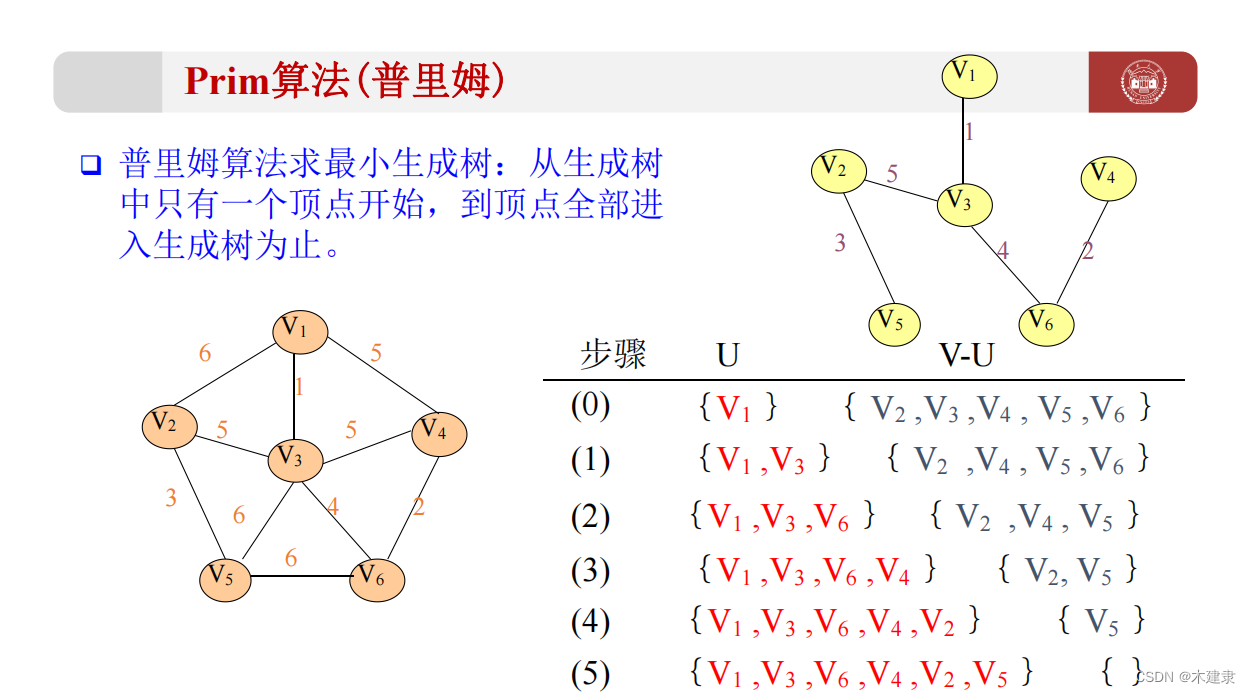
- 选择一个节点作为起始点,并将其加入生成树中。
- 选择与生成树相连的,最小的边,将其加入生成树中。
- 重复步骤2,直到所有节点都被加入生成树中。
复杂度
- 使用邻接矩阵表示图: O(V^2) V是顶点数量,每次都要找最小的顶点
- 使用邻接表表示图: O(ElogV) E是边的数量,每次都要找最小的顶点
(加入新节点的时候,把新节点所有相邻的,不在生成树中的边添加进去)
Kruskal算法
算法步骤
- 按照边的权值从小到大排序
- 依次选择边,如果选择后不会形成环,则加入生成树中(使用并查集判断新加入的边是否会形成环)
瓶颈生成树
定义
一个无向图G上的瓶颈生成树是G上一种特殊的生成树。一个瓶颈生成树T上权重最大边的权重是G中所有生成树中最小的。T上最大权重的边的权重称为T的值。 就是生成树T,的最大权值,是G中所有生成树中,最大权值的最小值。
单源最短路径
松弛算法
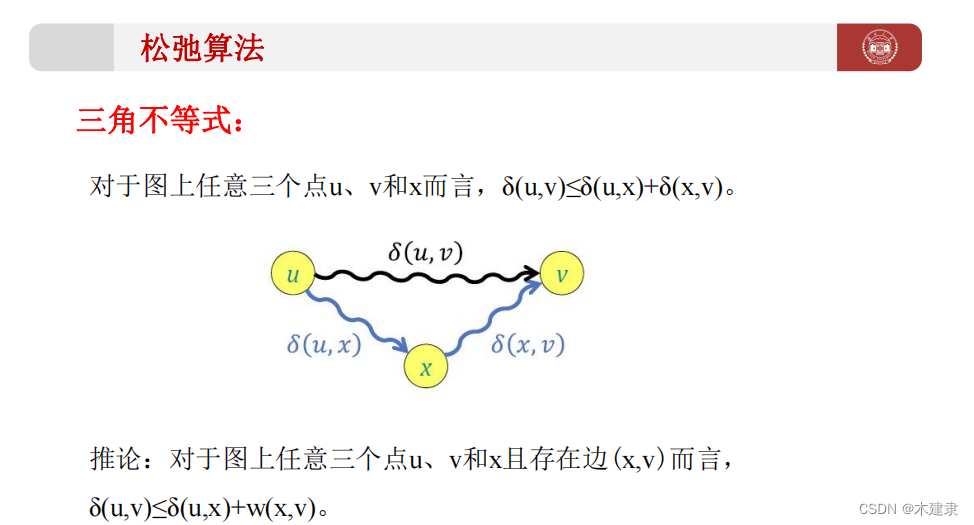
说人话就是,对于点u --> v , 如果找到另外一个点x,使得u --> x --> v的路径更短,则更新u --> v的路径。后面的Dijkstra算法Bellman-Ford算法是基于这个算法的。
Dijkstra算法
算法步骤
-
创建一个距离列表,其中包含每个节点到起始节点的距离。起始节点的距离设置为0,其他节点的距离设置为无穷大。
-
创建一个已访问列表和一个待访问列表。起始节点被标记为已访问,其他所有节点都被标记为待访问。
-
对于每一个待访问的节点,计算它到起始节点的距离。如果这个距离比当前记录的距离还要短,那么就更新这个节点的距离。
-
从待访问列表中找到距离最小的节点,将其标记为已访问,并将其从待访问列表中移除。
-
重复步骤3和4,直到所有的节点都被访问过。
-
距离列表中记录的就是每个节点到起始节点的最短距离。
缺点
无法解决边值为负值
Bellman-Ford算法
算法步骤
- 为每个顶点 ’ v '初始化距离数组 dist[]为dist[v] = INFINITY。假设任何顶点(假设为“0”)作为源并分配dist = 0。
- 根据以下条件放松所有edges(u,v,weight)N-1次:
- dist[v] = 最小值(dist[v],dist[u] + weight)
- 现在,再次放松所有边,即第N次,并基于以下两种情况,我们可以检测负循环:
- 情况 1(存在负循环):对于任何边(u,v,权重),如果 dist[u] + weight < dist[v]
- 情况 2(无负循环):情况 1 对于所有边均失败。
证明
N-1次可以求出最小路径
Bellman-ford算法思想是,进行一次遍历,遍历所有边,一次一定能找到一个距离start节点最近的点,N-1次之后,target节点最多和start节点之间有N-2个节点
N次距离减少,出现负循环回路
负权重的边又被遍历了一次
主定理
将规模为n的问题转化为a个规模为n/b的问题,花费的时间是O( n d n^d nd)
T(n)= a ∗ T ( n b ) + n d a*T(\frac{n}{b})+n^d a∗T(bn)+nd, 其中a>1 , b>1 , d>0
- 当 a < b d b^d bd , T(n)=O( n d n^d nd)
- 当 a = b d b^d bd , T(n)=O( n l o g b a ∗ l g n n^{log_{b} a}*lgn nlogba∗lgn)
- 当 a > b^d , T(n)=O( n l o g b a n^{log_{b} a} nlogba)
不想推导,直接记住吧
例子
二分查找
- T(n)= 2 T ( n 2 ) + 1 2T(\frac{n}{2})+1 2T(2n)+1
- a=2 b=2 d=0 --> O(n)
归并排序合并
- T(n)= 2 T ( n 2 ) + n 2T(\frac{n}{2})+n 2T(2n)+n
- a=2 b=2 d=1 --> O(n*lgn)
递归式子
- T(n)= 3 T ( n 4 ) + n l g n 3T(\frac{n}{4})+nlg{n} 3T(4n)+nlgn
- a=3 b=4 d约为1.5 --> O(n*lgn)
红黑树
定义
- 每个节点要么是黑色,要么是红色;
- 根和叶子都是黑色的,所有的叶子都是NIL;
- 红色节点的父节点是黑色的;
- 从节点x到其所有后代叶子节点的所有路径中包含相同数量
的黑节点。
相关文章:

算法设计与分析 笔记
截图摘自湖南大学彭鹏老师的ppt。笔记也是根据他的ppt整理的。 动态规划 核心 用数组记录中间结果,避免重复计算 三角数塔问题 问题描述 给定一个三角形数塔,从顶部出发,每次只能移动到下一行的相邻元素。要求找到一条路径,…...

mapreduce的工作原理
mapreduce的工作原理 MapReduce是一种编程模型,用于处理大规模数据集的并行运算。它的核心思想是"分而治之",即把一个大数据集分解成多个小块,由多个处理单元并行处理,然后再将结果合并以得到最终结果。MapReduce模型包…...

vue中v-bind和v-model有什么区别
在Vue.js中,v-bind和v-model都是指令,用于实现数据和DOM元素之间的双向绑定,但它们的使用场景和功能有所区别。 v-bind: v-bind是一个通用指令,用于动态地绑定一个或多个属性,或者一个组件prop到表达式。它可以绑定任何…...
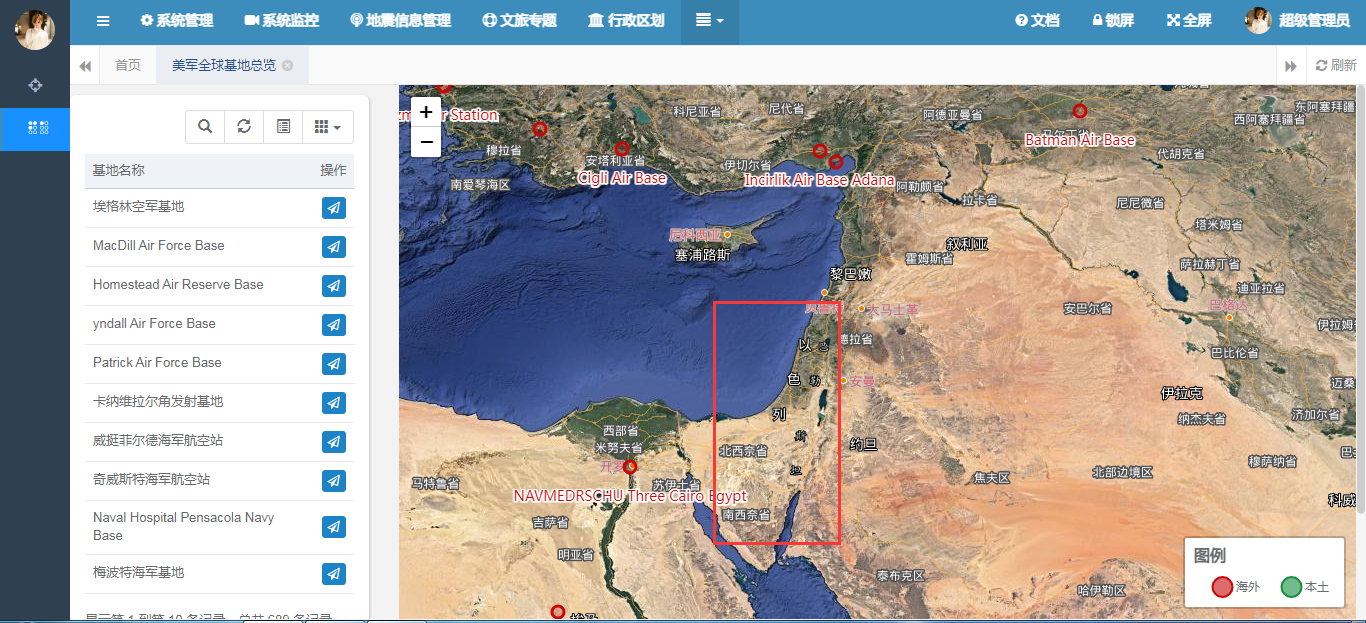
基于SpringBoot和PostGIS的某国基地可视化实战
目录 前言 一、Java后台开发设计与实现 1、模型层实现 2、控制层设计 二、WebGIS界面实现 1、列表界面的定义 2、全球基地可视化 三、成果展示 1、全球部署情况 2、亚太地区 3、欧洲基地分布 4、中东的部署 四、总结 前言 在之前的博客中,我们曾经对漂亮…...
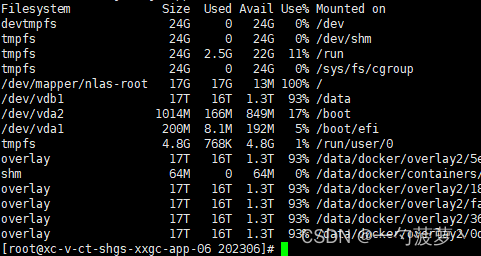
为什么Linux服务器空间充足而实际上空间已满的原因
以下是一个典型的Linux服务器的磁盘空间使用情况表,展示了不同文件系统的大小、已用空间、可用空间和挂载点等信息 磁盘空间表的基本组成 Linux服务器的磁盘空间使用情况通常通过df命令查看,输出的表格包含以下几列: Filesystem:…...

【LC刷题】DAY16:530 501 236
【LC刷题】DAY16:530 501 236 文章目录 【LC刷题】DAY16:530 501 236530. 二叉搜索树的最小绝对差 [link](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/description/)501.二叉搜索树中的众数236. 二叉树的最近公共祖先 [link](htt…...

Vue 3 的 Teleport 组件实现跨层级通信
突破组件边界 - 使用 Vue 3 的 Teleport 组件实现跨层级通信 你可能已经熟悉了组件的基本概念:每个组件都是一个独立的单元,拥有自己的模板、样式和逻辑。但是,有时候我们需要在不同层级的组件之间进行交互,这就需要用到 Vue 3 中新引入的 Teleport 组件。 Teleport 组件可以…...

chromadb
Chroma是一款AI开源向量数据库,用于快速构建基于LLM的应用,支持Python和Javascript语言。具备轻量化、快速安装等特点,可与Langchain、LlamaIndex等知名LLM框架组合使用。 官网: https://www.trychroma.com/ https://docs.trychr…...

Gradle 自动化项目构建-Gradle 核心之 Project
一、前言 从明面上看,Gradle 是一款强大的构建工具,但 Gradle 不仅仅是一款强大的构建工具,它更像是一个编程框架。Gradle 的组成可以细分为如下三个方面: groovy 核心语法:包括 groovy 基本语法、闭包、数据结构、面…...

简单介绍 Kamailio cfg_rpc 模块
记得先加载 cfg_rpc 模块 loadmodule "cfg_rpc.so" kamailio 起来之后 运行 kamcmd cfg.list 可以得到: dispatcher: probing_threshold dispatcher: inactive_threshold dispatcher: ping_reply_codes rtpengine: rtpengine_disable_tout rtpengine: a…...
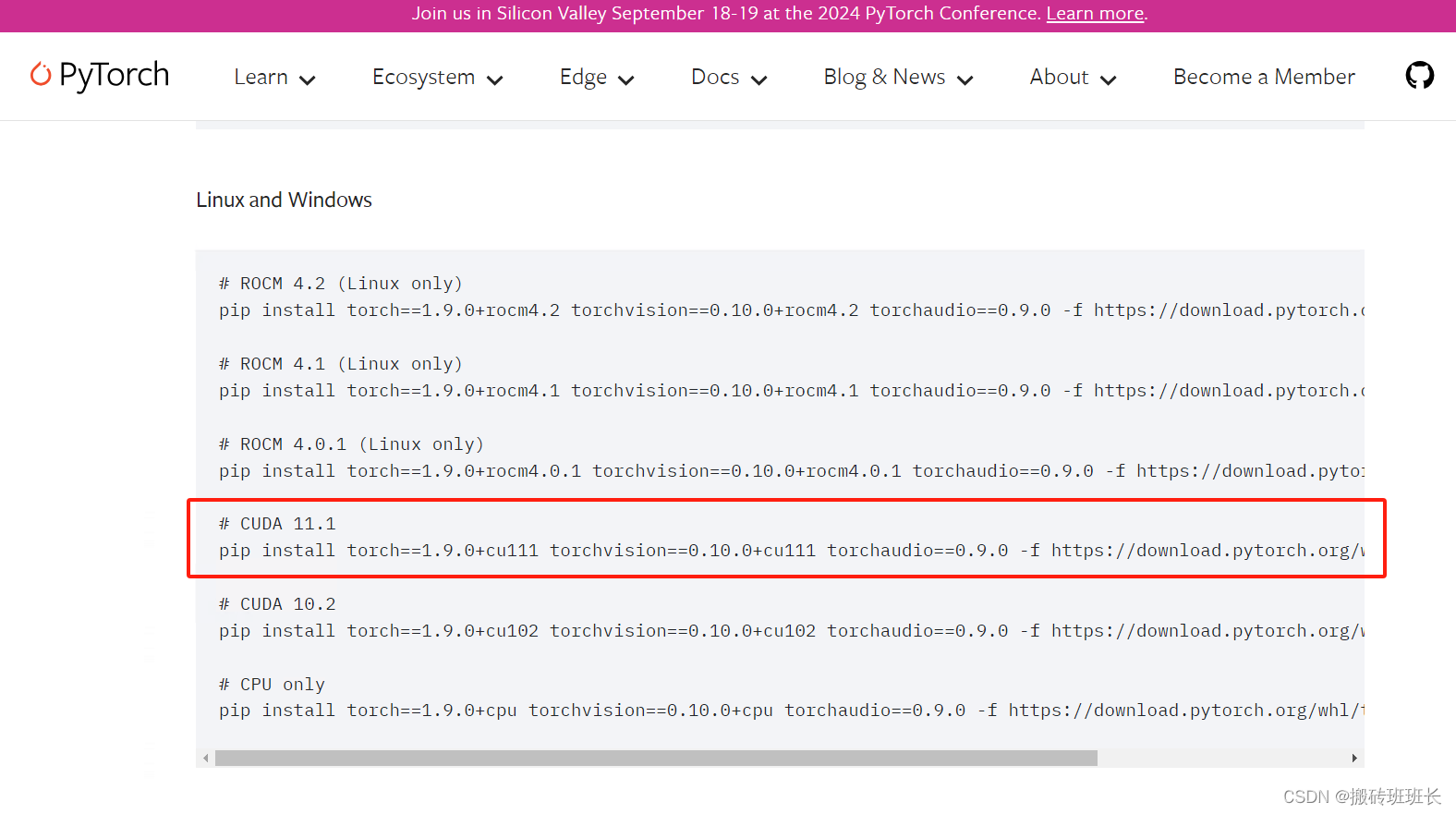
Windows 根据github上的环境需求,安装一个虚拟环境,安装cuda和torch
比如我们在github上看到一个关于运行环境的需求 Installation xxx系统Python 3.xxx CUDA 9.2PyTorch 1.9.0xxxxxx 最主要的就是cuda和torch,这两个会卡很多环境的安装。 我们重新走一遍环境安装。 首先创建一个虚拟环境 conda create -n 环境名字 python3.xxx…...

LeetCode 179. 最大数
更多题解尽在 https://sugar.matrixlab.dev/algorithm 每日更新。 组队打卡,更多解法等你一起来参与哦! LeetCode 179. 最大数,难度中等。 排序 解题思路:现将 int 类型转成 str 类型,然后进行字符串比较,…...
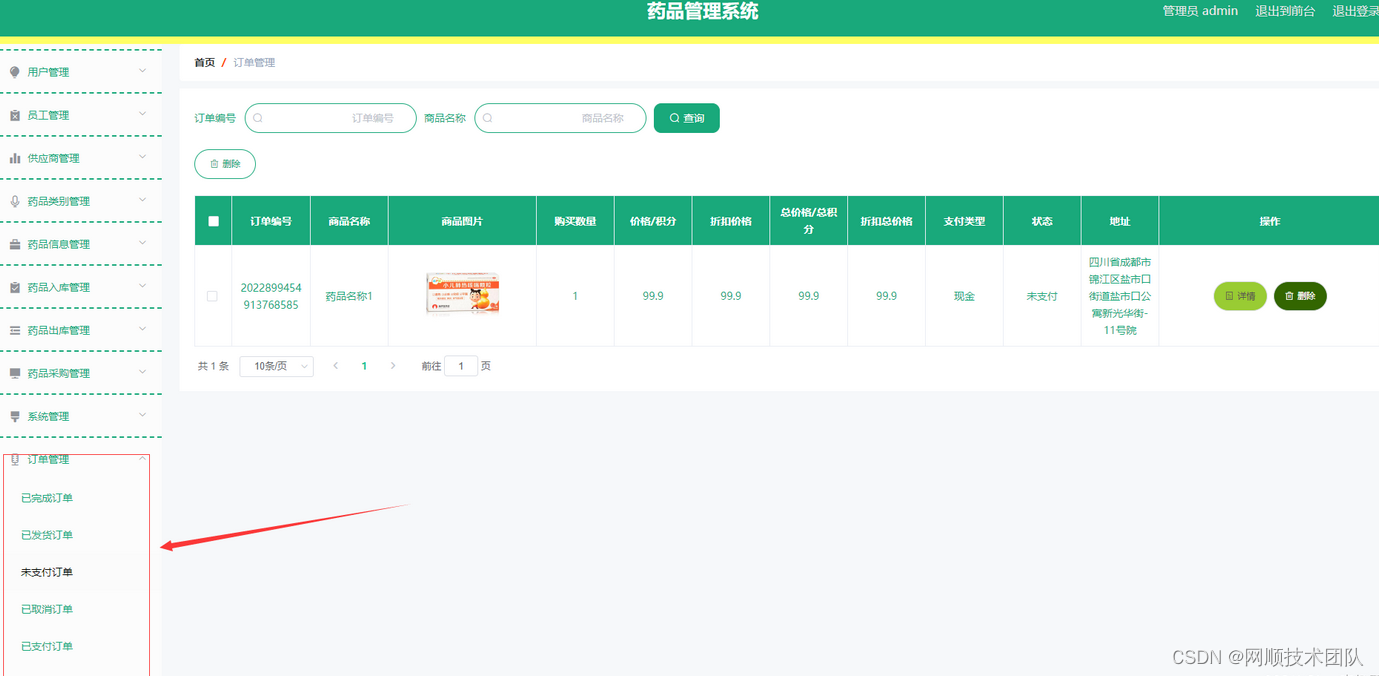
基于Java+SpringBoot+vue+elementui药品商城采购系统详细设计实现
基于JavaSpringBootvueelementui药品商城采购系统详细设计实现 🍅 作者主页 网顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承接各种…...
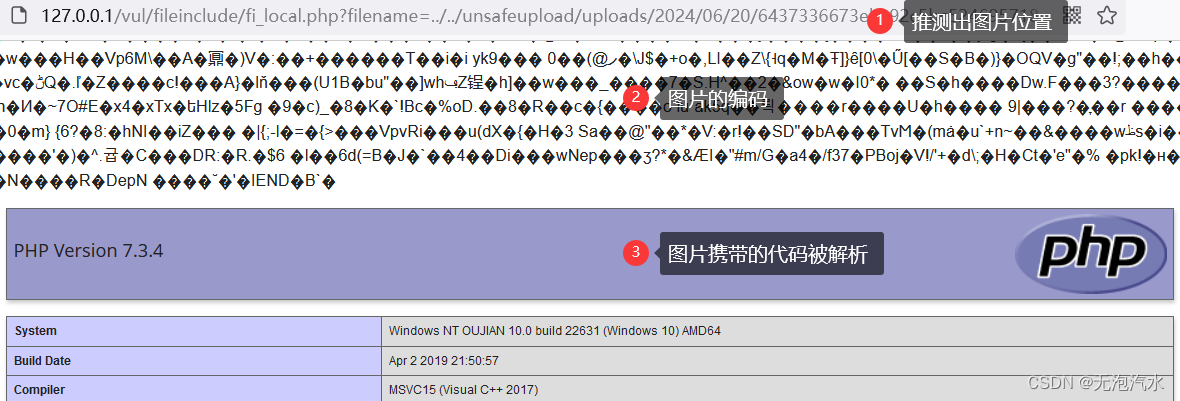
Pikachu靶场--文件上传
参考借鉴 Pikachu靶场之文件上传漏洞详解_皮卡丘文件上传漏洞-CSDN博客 文件上传漏洞:pikachu靶场中的文件上传漏洞通关_pikachu文件上传通关-CSDN博客 client check 在桌面新建一个文件夹,准备一个hello.php文件,文件写入如下代码 <?p…...

突破架构瓶颈:克服软件系统中的漂移和侵蚀
一种常见但不完美的比喻是将软件系统中的架构漂移和侵蚀与物理建筑的架构相比。虽然这个比喻很直观,但它存在一个根本性的误解,这也常常引发软件开发中的架构问题。 试想一下,一个设计良好的摩天大楼或房屋建成后,我们期望它基本保…...

每日练题(py,c,cpp).6_19,6_20
检验素数 from math import sqrt a int(input("请输入一个数:")) for i in range(2,int(sqrt(a))):if a%i 0:print("该数不是素数")breakelse: print("该数是素数")# # 1既不是素数也不是合数 # #可以用flag做标志位 # b int(…...

居中显示-css样式
在微信小程序中,要让一个盒子(子元素)在另一个盒子(父元素)内部居中显示,可以使用以下几种方法: 1. 使用 Flex 布局 微信小程序支持使用类似于 CSS Flexbox 的布局方式。以下是使用 Flex 布局的…...

生骨肉冻干喂猫比较好?热门、口碑好、值得入手生骨肉冻干力荐
随着科学养猫的普及,生骨肉冻干喂养越来越受欢迎,生骨肉冻干喂养对猫的好处很多,它符合猫咪的天性,可以提供全面的营养,保持牙齿和牙龈的健康,还有助于维持健康的消化系统。虽然许多猫主人看到了生骨肉冻干…...
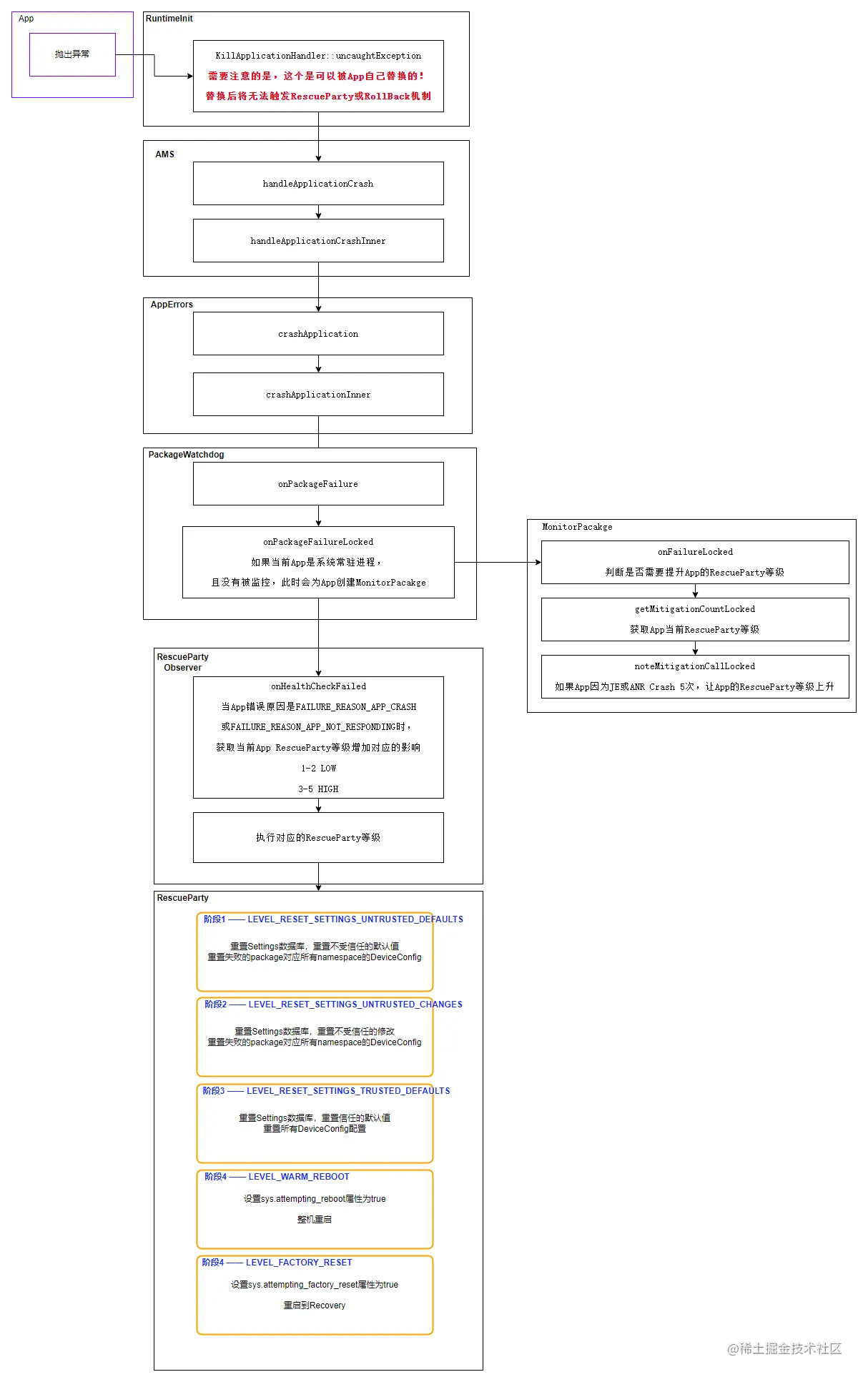
【安卓13 源码】RescueParty救援机制
RescueParty机制正是在这个背景下诞生的,当它注意到系统或系统核心组件陷入循环崩溃状态时,就会根据崩溃的程度执行不同的救援行动,以期望让设备恢复到正常使用的状态。 开机后会自动重启,进入Recovery界面。经查找,是…...

详细介绍iutils.dll丢失的多个解决方法,一键快速修复丢失的iutils.dll文件
当用户遭遇“iutils.dll缺失”的提示时,这通常预示着依赖该库文件的程序将面临启动失败或功能受限的风险。DLL(Dynamic Link Library,动态链接库)文件无疑占据了核心地位。这些文件就如同建筑师手中的蓝图,为软件的构建…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
