AcWing算法基础课笔记——高斯消元
高斯消元
用来求解方程组
a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 … a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n = b_1\\ a_{21} x_1 + a_{22} x_2 + \dots + a_{2n} x_n = b_2\\ \dots \\ a_{n1} x_1 + a_{n2} x_2 + \dots + a_{nn} x_n = b_n\\ a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2…an1x1+an2x2+⋯+annxn=bn
输入是 n × ( n − 1 ) n \times (n -1 ) n×(n−1)的矩阵。
对方程组进行以下三种初等行列变换后,方程的解不变:
- 把某一行乘以一个非零的数
- 交换某2行
- 把某行的若干倍加到另一行上去
因此,对任意一个方程组,可以把它变成倒三角形式:
a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 22 x 2 + ⋯ + a 2 n x n = b 2 … a ( n − 1 ) ( n − 1 ) x n − 1 + a ( n − 1 ) n x n = b n − 1 a n n x n = b n a_{11}x_1 + a_{12}x_2+\dots +a_{1n}x_n = b_1 \\ a_{22}x_2 + \dots + a_{2n} x_n = b_2 \\ \dots \\ a_{(n-1)(n-1)}x_{n-1} +a_{(n-1)n}x_{n} = b_{n-1}\\ a_{nn}x_n = b_n a11x1+a12x2+⋯+a1nxn=b1a22x2+⋯+a2nxn=b2…a(n−1)(n−1)xn−1+a(n−1)nxn=bn−1annxn=bn
有三种情况:
- 完美阶梯型——唯一解
- 0 = 非零 ———无解
- 0 = 0 ——无穷多组解
高斯消元步骤:
枚举每一列c:
- 找到绝对值最大的一行
- 将该行换到最上面
- 将该行第一个数变成1
- 将下面所有行的第c列消成0
题目
详见:https://www.acwing.com/problem/content/description/885/
输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 m 个方程 n 个未知数的线性方程组示例:
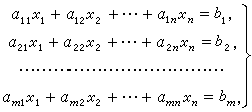
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个实数,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解,结果保留两位小数。
注意:本题有 SPJ,当输出结果为 0.00 时,输出 -0.00 也会判对。在数学中,一般没有正零或负零的概念,所以严格来说应当输出 0.00,但是考虑到本题作为一道模板题,考察点并不在于此,在此处卡住大多同学的代码没有太大意义,故增加 SPJ,对输出 -0.00 的代码也予以判对。
如果给定线性方程组存在无数解,则输出 Infinite group solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数,绝对值均不超过 100。
输入样例:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例:
1.00
-2.00
3.00
代码
#include<iostream>
#include<algorithm>
#include<cmath>using namespace std;const int N = 110;
const double eps = 1e-6;int n;
double a[N][N];int gauss() {int c, r;for(c = 0, r = 0; c < n; c ++ ) {// 找到绝对值最大的一行 t int t = r;for(int i = r; i < n; i ++ ) {if(fabs(a[i][c]) > fabs(a[t][c])) {t = i;}}if(fabs(a[t][c]) < eps) continue; //如果第t行为0,结束//将该行换到最上面 for(int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); //将该行的第c位设为1(前面都为0) for(int i = n; i >= c; i --) a[r][i] /= a[r][c];//将下面所有行的第c列消成0//也就是从r + 1行开始,对于第i行,第i行第c个位置a[i][c]如果不为0的话,就要消成0// a[i][c]消成0 : a[i][c] -= a[r][c] * a[i][c] a[r][c]为1// 那么其他所有列: a[i][j] -= a[r][j] * a[i][c]for(int i = r + 1; i < n; i ++ ) {if(fabs(a[i][c]) > eps) {for(int j = n; j >= c; j -- ) {a[i][j] -= a[r][j] * a[i][c];}}}r ++; }if(r < n) {for(int i = r; i < n; i ++ ) {if(fabs(a[i][n]) > eps)return 2; //无解 }return 1; //有无穷多组解 }//求解唯一解 //从第n - 1 行开始往上,遍历每一行//对于第i行,它的解是a[i][n]的值 for(int i = n - 1; i >= 0; i -- ) {for(int j = i + 1; j < n; j ++ ) {a[i][n] -= a[i][j] * a[j][n];}}return 0; //有唯一解 } int main() {cin >> n;for(int i = 0; i < n; i ++ ) {for(int j = 0; j <= n; j ++ ) {cin >> a[i][j];}}int t = gauss();if(t == 0) {for(int i = 0; i < n; i ++ ) printf("%.2lf\n", a[i][n]);}else if (t == 1) puts("Infinite group solutions");else puts("No solution");return 0;
}
相关文章:
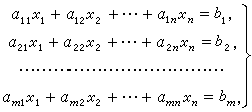
AcWing算法基础课笔记——高斯消元
高斯消元 用来求解方程组 a 11 x 1 a 12 x 2 ⋯ a 1 n x n b 1 a 21 x 1 a 22 x 2 ⋯ a 2 n x n b 2 … a n 1 x 1 a n 2 x 2 ⋯ a n n x n b n a_{11} x_1 a_{12} x_2 \dots a_{1n} x_n b_1\\ a_{21} x_1 a_{22} x_2 \dots a_{2n} x_n b_2\\ \dots \\ a…...

【JavaScript脚本宇宙】图形魔术:探索领先的图像处理库及其独特功能
深入了解HTML5视频:最受欢迎的库及其功能 前言 图像处理是现代数字媒体开发中不可或缺的一部分,从调整图像大小到创建复杂的图形场景。有许多库可用,每个库都有其特定的优点和适用场景。在本文中,我们将探讨六种流行的图像处理库…...

Nemotron-4
Nemotron-4是英伟达(NVIDIA)发布的一系列高级人工智能模型,特别着重于大尺度语言模型(LLMs)的发展。这些模型在不同的参数量级上展现出了卓越的性能和效率,其中特别提到了150亿参数的Nemotron-4 15B和3400亿…...

【神经网络】神经元的基本结构和训练过程
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步! 神经元的基本结构和训练过程 …...
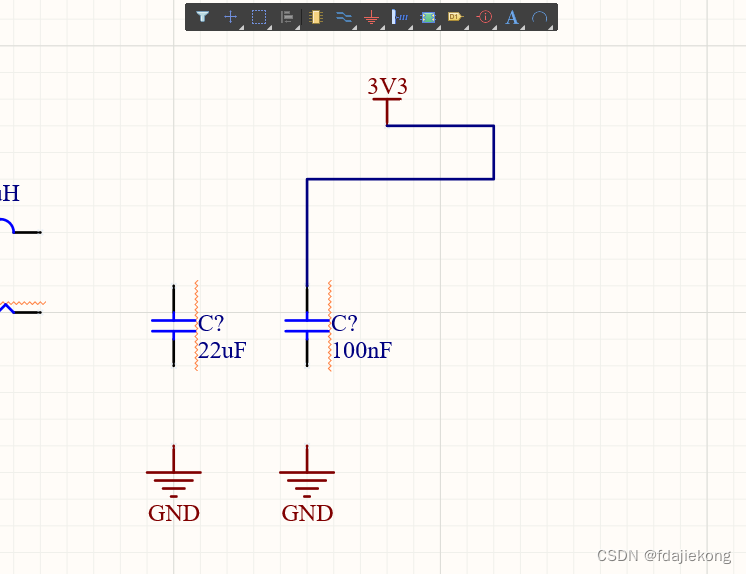
第28课 绘制原理图——绘制导线
概述 放置完元器件之后,接着就要用导线将元器件的管脚一个一个连起来了。 绘制导线的方法 点击快速工具条上的“线”命令,进入绘制导线的过程。 点击选择某个管脚或电源端口,作为导线的起始端。 再点击选择另一个管脚或电源端口,…...

NLP 相关知识
NLP 相关知识 NLPLLMPrompt ChainingLangChain NLP NLP(Natuarl Language Processing)是人工智能的一个分支,中文名自然语言处理,专注于处理和理解人类使用的自然语言。它涵盖了多个子领域,如文本分类、情感分析、机器…...

Java中的设计模式:实战案例分享
Java中的设计模式:实战案例分享 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 设计模式是软件开发中的宝贵工具,它们为常见的问题提供…...
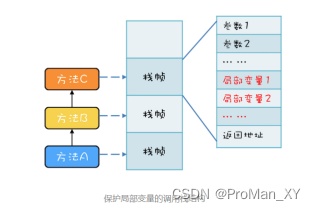
并发编程理论基础——合适的线程数量和安全的局部变量(十)
多线程的提升方向 主要方向在于优化算法和将硬件的性能发挥到极致想要发挥出更多的硬件性能,最主要的就是提升I/O的利用率和CPU的利用率以及综合利用率操作系统已经解决了磁盘和网卡的利用率问题,利用中断机制还能避免 CPU 轮询 I/O 状态,也提…...

Python使用抽象工厂模式和策略模式的组合实现生成指定长度的随机数
设计模式选择理由: 抽象工厂模式: 抽象工厂模式适合于创建一组相关或依赖对象的场景。在这里,我们可以定义一个抽象工厂来创建不同类型(数字、字母、特殊符号)的随机数据生成器。 策略模式: 策略模式允许你…...

python-17-零基础自学python-
学习内容:《python编程:从入门到实践》第二版 知识点: 类、子类、继承、调用函数 练习内容: 练习9-6:冰激凌小店 冰激凌小店是一种特殊的餐馆。编写一个名为IceCreamStand的类,让它继承为完成练习9-1或…...

Web应用和Tomcat的集成鉴权1-BasicAuthentication
作者:私语茶馆 1.Web应用与Tomcat的集成式鉴权 Web应用部署在Tomcat时,一般有三层鉴权: (1)操作系统鉴权 (2)Tomcat容器层鉴权 (3)应用层鉴权 操作系统层鉴权包括但不限于:Tomcat可以和Windows的域鉴权集成,这个适合企业级的统一管理。也可以在Tomcat和应用层独立…...

解决Linux下Java应用因内存不足而崩溃的问题
在Linux系统中运行内存密集型的Java应用时,经常会遇到因系统内存不足而导致应用崩溃的问题。本文将探讨如何诊断这类问题以及提供有效的解决方案。 问题诊断 首先,使用 free -h 命令查看系统的内存使用情况,得到以下输出: total…...
ardupilot开发 --- 视觉伺服 篇
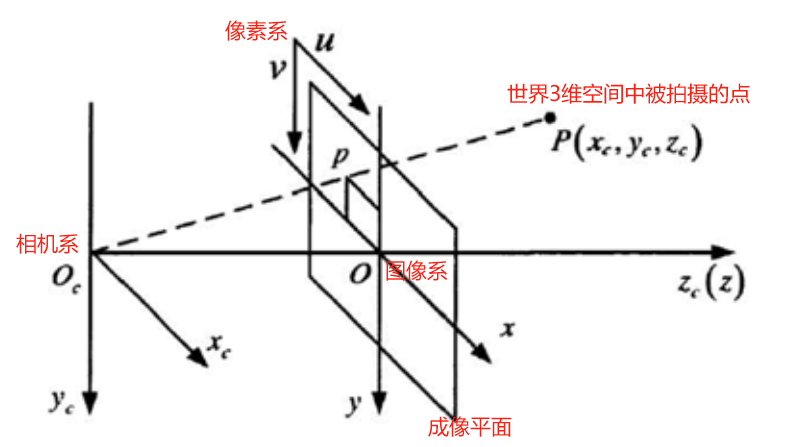
风驰电掣云端飘,相机无法对上焦 1.视觉伺服分类2.视觉伺服中的坐标系3.成像模型推导4.IBVS理论推导5.IBVS面临的挑战6.visp 实践参考文献 1.视觉伺服分类 控制量是在图像空间中推导得到还是在欧式空间中推导得到,视觉伺服又可以分类为基于位置(PBVS)和基…...

KVM配置嵌套虚拟化
按照以下步骤启用、配置和开始使用嵌套虚拟化,默认情况下禁用该功能,要启用它,请在宿主机物理机上进行配置。在centos stream 9和ubuntu 22部署kvm默认支持虚拟机嵌套虚拟化。 1、英特尔 1.1检查嵌套虚拟化在您的主机系统上是否可用 $cat /sys/module/kvm_intel/paramete…...

Springboot应用的信创适配-补充
Springboot应用的信创适配-CSDN博客 因为篇幅限制,这里补全Spring信创适配、数据库信创适配、Redis信创适配、消息队列信创适配等四个章节。 Springboot应用的信创适配 Springboot应用的信创适配,如上图所示需要适配的很多,从硬件、操作系统、…...

制图工具(14)导出图层字段属性信息表
在制图工具(13)地理数据库初始化工具中我们提到,有一个参数为:“输入Excel表”,并要求表格中的图层字段属性项需要按工具的帮助文档中的示例进行组织… 如下图: 此外,总有那个一个特别的需求&am…...

代码随想录——买股票的最佳时机Ⅱ(Leecode122)
添加链接描述 贪心 局部最优:手机每天的正利润 全局最优:求最大利润 class Solution {public int maxProfit(int[] prices) {int res 0;for(int i 1; i < prices.length; i){res Math.max(prices[i] - prices[i - 1], 0);}return res;} }...
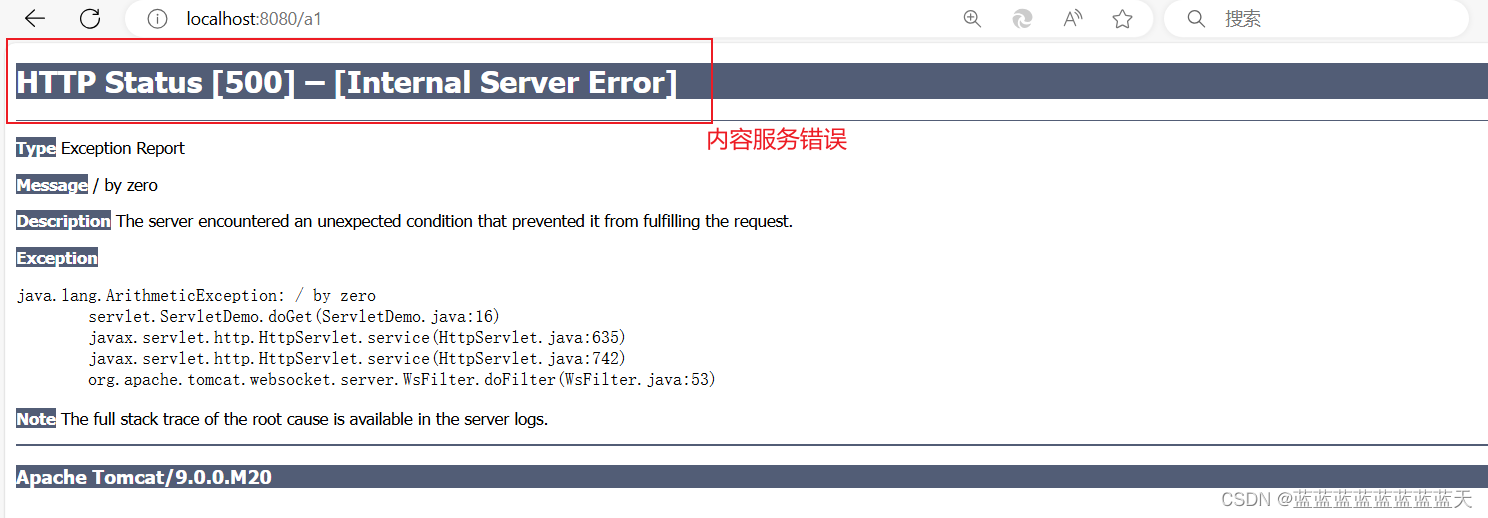
使用Servlet开发javaweb,请求常见错误详解及其解决办法【404、405、500】
Servlet报错的情况多种多样,涵盖了配置错误、代码逻辑错误、资源未找到、权限问题等多个方面。以下是一些常见的Servlet报错情况及其可能的原因和解决方法: 404 Not Found: 错误原因图示: URL映射 发送请求,出现404错误 原因: 请…...
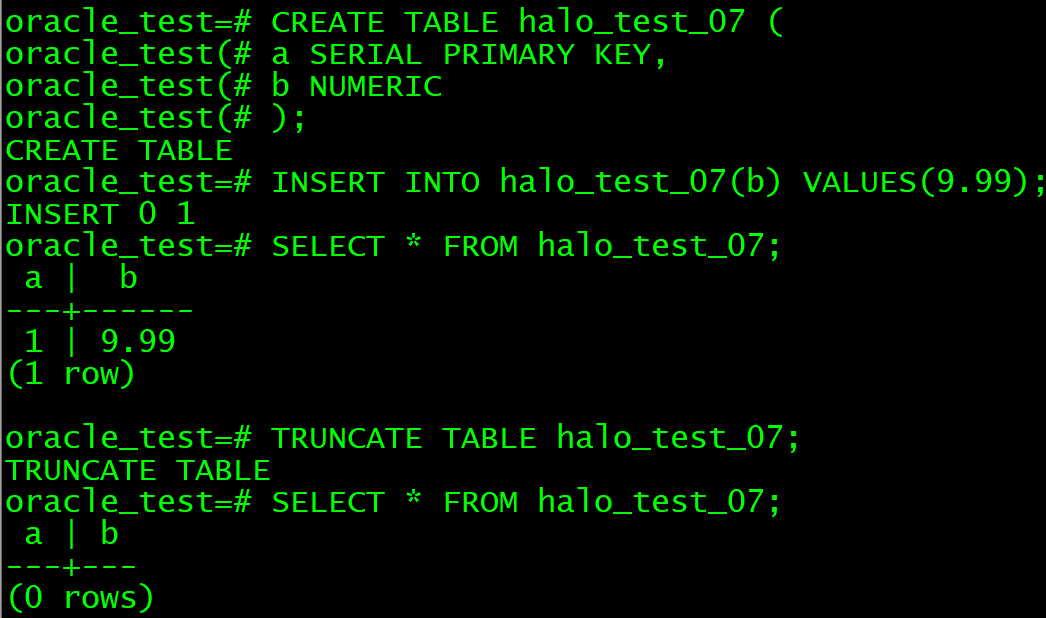
数据库管理-第210期 HaloDB-Oracle兼容性测试02(20240622)
数据库管理210期 2024-06-22 数据库管理-第210期 HaloDB-Oracle兼容性测试02(20240622)1 表增加列2 约束3 自增列4 虚拟列5 表注释6 truncat表总结 数据库管理-第210期 HaloDB-Oracle兼容性测试02(20240622) 作者:胖头…...

SpringBoot实现定时任务的动态停止和更新
目录 定时任务管理器定时任务的任务接口定时任务和定时任务结果的缓存对象定时任务使用姿势 定时任务管理器 负责启动一个定时任务、停止一个定时任务、更新一个定时任务 /*** 定时任务管理器* 1、创建并启动一个定时任务* 2、停止一个定时任务* 3、更新一个定时任务*/ publi…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
