ardupilot开发 --- 视觉伺服 篇
风驰电掣云端飘,相机无法对上焦
- 1.视觉伺服分类
- 2.视觉伺服中的坐标系
- 3.成像模型推导
- 4.IBVS理论推导
- 5.IBVS面临的挑战
- 6.visp 实践
- 参考文献
1.视觉伺服分类
控制量是在图像空间中推导得到还是在欧式空间中推导得到,视觉伺服又可以分类为基于位置(PBVS)和基于图像的(IBVS)视觉伺服。

2.视觉伺服中的坐标系
- 概述
世界坐标系W:用于测量(估计)飞机、机器人的位姿(位置和姿态)。
飞机机体坐标系B:最终运动控制量应转换到这个坐标系。
目标机体坐标系O:用于描述目标物体与相机间的位姿,用于描述相机坐标系和目标物体机体坐标系之间的位姿关系。
相机坐标系C:是推导IBVS最重要的坐标系。
图像坐标系I:是描述特征点运动状态的坐标系。
像素坐标系P:最终的图像数据最终以该坐标系的形式存储信息。 - 表示
W 即 world,表示世界坐标系,E即 end,表示末端坐标系,类似还有I表示 image,O表示 object,C 表示 Camera等。而各种坐标系齐次变换矩阵T的左上标表示转换后的坐标系,右下标表示转换前的坐标系。如 c T e ^{c}T_e cTe或 c V e ^{c}V_e cVe表示从末端坐标系E到相机坐标系C的坐标变换矩阵或称为齐次变换矩阵(齐次变换矩阵即旋转变换和位移变换融合到了一个矩阵当中)。

3.成像模型推导
-
相关概念:透视投影模型。
-
关于透视投影这篇文章讲的很好: 深蓝AI:经典干货|相机模型与张氏标定。参考了这篇文章。
-
小孔成像模型
光心位于成像平面的前方,成倒立的像,这样不方便IBVS的推导。

-
透视投影模型
光心位于成像平面的后方,成正立的实像,更符合实际成像过程,方便IBVS的推导。

-
世界系、相机系、图像系、像素系的轴向、原点位置示意图

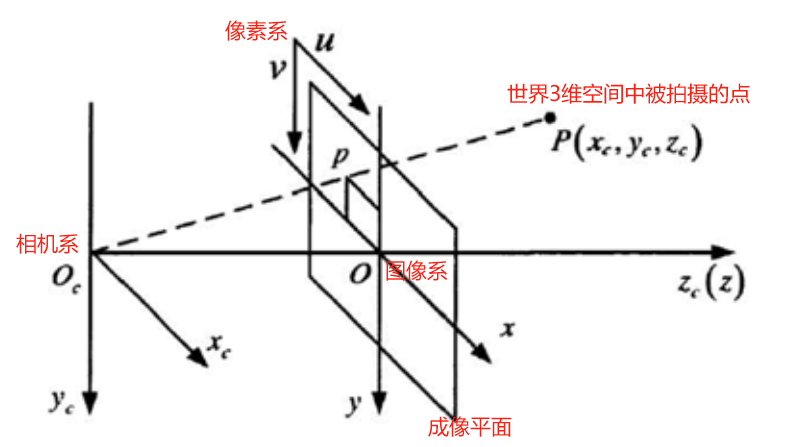

相机系记作Oc-XcYcZc.
图像系记作o-xy.
像素系记作o-uv.
相机系的原点在光心,Xc轴水平向右,Yc轴竖直向下,Zc轴水平向前。
图像坐标系的原点在Zc轴与成像平面的交点处,x、y轴分别与Xc、Yc轴同向。
像素坐标系的原点在成像平面的左上角,u、v轴分别与图像系的x、y轴同向。
图像系原点在像素系中的坐标为【u0,v0】,也被称为主点坐标。
相机系原点到成像平面的距离为 f,即焦距。 -
像素系坐标与图像系坐标间的关系
{ u = x d x + u 0 = p x + u 0 v = x d x + u 0 = p x + u 0 (式 1 ) \begin{cases} u=\frac x {dx}+u_0=p_x+u_0 \\ v=\frac x {dx}+u_0=p_x+u_0 \end{cases}(式1) {u=dxx+u0=px+u0v=dxx+u0=px+u0(式1)
其中:
[u0,v0]是图像系原点在像素系中的坐标;
px,py是图像系中 xy 轴的单位长度对应的像素个数;
uv是像素系中的坐标;
xy是图像系中的坐标。 -
图像系坐标与相机系坐标间的关系
{ x = f Z X y = f Z Y (式 2 ) \begin{cases} x=\frac f {Z}X \\ y=\frac f {Z}Y \end{cases}(式2) {x=ZfXy=ZfY(式2)
其中:
f f f 是相机焦距;
x y xy xy 是图像系中的坐标;
X Y Z XYZ XYZ 是目标点在相机系中的坐标。 -
相机内参
(式1)、(式2) 提到的参数 u 0 , v 0 , p x , p y u_0,v_0,px,p_y u0,v0,px,py 被称为相机的内参,通过相机标定得到。
4.IBVS理论推导

问题描述:
假设在世界3维空间中有一点P,
在相机系中的坐标记作 [ X , Y , Z ] [X,Y,Z] [X,Y,Z],
在图像系中的坐标记作 [ x , y ] [x,y] [x,y],
在像素系中的坐标记作 [ u , v ] [u,v] [u,v]。
记相机的6自由度运动速度矢量(相机坐标系的速度矢量)为:
V c = [ v x , v y , v z , w x , w y , w z ] T (式 3 ) V_c=[v_x,v_y,v_z,w_x,w_y,w_z]^T(式3) Vc=[vx,vy,vz,wx,wy,wz]T(式3)
根据物体的旋转运动和直线运动的经典理论公式,可得到点P在相机系中的运动方程为:
[ X ˙ Y ˙ Z ˙ ] = − [ v x v y v z ] − [ w x w y w z ] × [ X Y Z ] (式 4 ) \begin{bmatrix} \dot{X} \\ \dot{Y} \\ \dot{Z} \end{bmatrix} = - \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix} - \begin{bmatrix} w_x \\ w_y \\ w_z \end{bmatrix} \times \begin{bmatrix} {X} \\ {Y} \\ {Z} \end{bmatrix}(式4) X˙Y˙Z˙ =− vxvyvz − wxwywz × XYZ (式4)
注意:因为 V c = [ v x , v y , v z , w x , w y , w z ] T V_c=[v_x,v_y,v_z,w_x,w_y,w_z]^T Vc=[vx,vy,vz,wx,wy,wz]T是相机的速度矢量,正好与点P的速度矢量相反,因此(式4)右边取的是负号!!
将(式2)对时间求导可得:
{ x ˙ = X ˙ / Z − X Z ˙ / Z 2 y ˙ = Y ˙ / Z − Y Z ˙ / Z 2 (式 5 ) \begin{cases} \dot{x}=\dot{X}/Z-X\dot{Z}/Z^2\\ \dot{y}=\dot{Y}/Z-Y\dot{Z}/Z^2\\ \end{cases}(式5) {x˙=X˙/Z−XZ˙/Z2y˙=Y˙/Z−YZ˙/Z2(式5)
将(式2)和(式4)代入(式5)可得:
{ x ˙ = − v x / Z + x v z / Z + x y w x − ( 1 + x 2 ) w y + y w z y ˙ = − v y / Z + y v z / Z − x y w y + ( 1 + y 2 ) w x − x w z (式 6 ) \begin{cases} \dot{x}=-v_x/Z+xv_z/Z+xyw_x-(1+x^2)w_y+yw_z\\ \dot{y}=-v_y/Z+yv_z/Z-xyw_y+(1+y^2)w_x-xw_z\\ \end{cases}(式6) {x˙=−vx/Z+xvz/Z+xywx−(1+x2)wy+ywzy˙=−vy/Z+yvz/Z−xywy+(1+y2)wx−xwz(式6)
写成矩阵形式:
s ˙ = [ x ˙ y ˙ ] = L s V c (式 7 ) \dot{s}= \begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix} =L_sV_c(式7) s˙=[x˙y˙]=LsVc(式7)
其中 s s s 被称为视觉特征, L s L_s Ls被称为图像雅可比矩阵或相互作用矩阵:
L s = [ − 1 / Z 0 x / Z x y − ( 1 + x 2 ) y 0 − 1 / Z y / Z 1 + y 2 − x y − x ] (式 8 ) L_s= \begin{bmatrix} -1/Z&0&x/Z&xy&-(1+x^2)&y \\ 0&-1/Z&y/Z&1+y^2&-xy&-x \end{bmatrix} (式8) Ls=[−1/Z00−1/Zx/Zy/Zxy1+y2−(1+x2)−xyy−x](式8)
记视觉特征 s s s的期望值为 s d s_d sd,则视觉特征误差为:
s e = s − s d (式 9 ) s_e=s-s_d(式9) se=s−sd(式9)
因为 s d s_d sd是常量因此有:
s ˙ d = 0 (式 10 ) \.s_d=0(式10) s˙d=0(式10)
将(式9)对时间求导,得到误差系统的状态空间方程:
s ˙ e = s ˙ − s ˙ d = L s V c (式 11 ) \.s_e=\.s-\.s_d=L_sV_c(式11) s˙e=s˙−s˙d=LsVc(式11)
设计一个控制律 V c Vc Vc使得(式11)表示的误差系统的全部状态随着时间呈指数衰减到0,即控制律使得最终的误差系统变成如下形式:
s ˙ e = − λ s e (式 12 ) \.s_e=-\lambda s_e(式12) s˙e=−λse(式12)
那么可以反推出控制律:
V c = − λ L s + s e (式 13 ) V_c=-\lambda L_s^+ s_e(式13) Vc=−λLs+se(式13)
其中 L s + L_s^+ Ls+是 L s L_s Ls的广义逆矩阵, λ \lambda λ是一个常量。
待续…
5.IBVS面临的挑战
- 计算 L s + L_s^+ Ls+时会产生奇异值。
- L s L_s Ls不容易得到, L s L_s Ls的几种计算方式请参考:https://zhuanlan.zhihu.com/p/422634446
- 待续…
6.visp 实践
- cJc :相机坐标系的运动控制自由度,可以看作是运动控制自由度雅可比矩阵。
- L:图像雅可比矩阵,相互作用矩阵
- J1:task雅可比矩阵
- signInteractionMatrix:相互作用矩阵的符号,1 for eye-in-hand, -1 for eye-to-hand
- inversionType:指定求广义逆矩阵还是求转置矩阵
- Transpose matrix:转置矩阵
- Inverse matrix:逆矩阵
- task Jacobian 是什么?J1???
V c = − λ L ^ s + e V_c = -\lambda {\widehat {\bf L}}^{+}_{s} {\bf e} Vc=−λL s+e,得到的控制律 V c V_c Vc是相机系的运动矢量!
V e = − λ ( L ^ s c V e ∗ e J e ) + e {V_e }= -\lambda \left( {{\widehat {\bf L}}_{s} {^c}{\bf V}_e* {^e}{\bf J}_e} \right)^{+} {\bf e} Ve=−λ(L scVe∗eJe)+e,得到的控制律 V e V_e Ve是终端系的运动矢量!
其中 L ^ s \widehat {L}_s L s是 L s L_s Ls的估计值!
why ??
推导如下:
s ˙ = L s V c \dot{s}=L_sV_c s˙=LsVc
记终端系的速度矢量为 V e V_e Ve,终端系到相机系的坐标变换矩阵为 c V e ^cV_e cVe,允许控制的速度矢量自由度记为 e J e ^eJe eJe,则:
s ˙ = L s V c = L s c V e e J e V e \dot{s}=L_sV_c=L_s^cV_e{^eJe}V_e s˙=LsVc=LscVeeJeVe
那么控制率就变成了:
V e = − λ ( L s c V e e J e ) − 1 V_e=-\lambda (L_s{^cV_e}^eJe)^{-1} Ve=−λ(LscVeeJe)−1
对于无人机视觉伺服, c V e ^cV_e cVe即飞机机体坐标系FRD到相机系RDF的齐次变换矩阵(坐标变换)!!!!
参考文献
https://zhuanlan.zhihu.com/p/422634446
https://zhuanlan.zhihu.com/p/389903710
深蓝AI:经典干货|相机模型与张氏标定
硕士论文:基于无标定视觉伺服的定位研究-王博
相关文章:

ardupilot开发 --- 视觉伺服 篇
风驰电掣云端飘,相机无法对上焦 1.视觉伺服分类2.视觉伺服中的坐标系3.成像模型推导4.IBVS理论推导5.IBVS面临的挑战6.visp 实践参考文献 1.视觉伺服分类 控制量是在图像空间中推导得到还是在欧式空间中推导得到,视觉伺服又可以分类为基于位置(PBVS)和基…...

KVM配置嵌套虚拟化
按照以下步骤启用、配置和开始使用嵌套虚拟化,默认情况下禁用该功能,要启用它,请在宿主机物理机上进行配置。在centos stream 9和ubuntu 22部署kvm默认支持虚拟机嵌套虚拟化。 1、英特尔 1.1检查嵌套虚拟化在您的主机系统上是否可用 $cat /sys/module/kvm_intel/paramete…...

Springboot应用的信创适配-补充
Springboot应用的信创适配-CSDN博客 因为篇幅限制,这里补全Spring信创适配、数据库信创适配、Redis信创适配、消息队列信创适配等四个章节。 Springboot应用的信创适配 Springboot应用的信创适配,如上图所示需要适配的很多,从硬件、操作系统、…...

制图工具(14)导出图层字段属性信息表
在制图工具(13)地理数据库初始化工具中我们提到,有一个参数为:“输入Excel表”,并要求表格中的图层字段属性项需要按工具的帮助文档中的示例进行组织… 如下图: 此外,总有那个一个特别的需求&am…...

代码随想录——买股票的最佳时机Ⅱ(Leecode122)
添加链接描述 贪心 局部最优:手机每天的正利润 全局最优:求最大利润 class Solution {public int maxProfit(int[] prices) {int res 0;for(int i 1; i < prices.length; i){res Math.max(prices[i] - prices[i - 1], 0);}return res;} }...
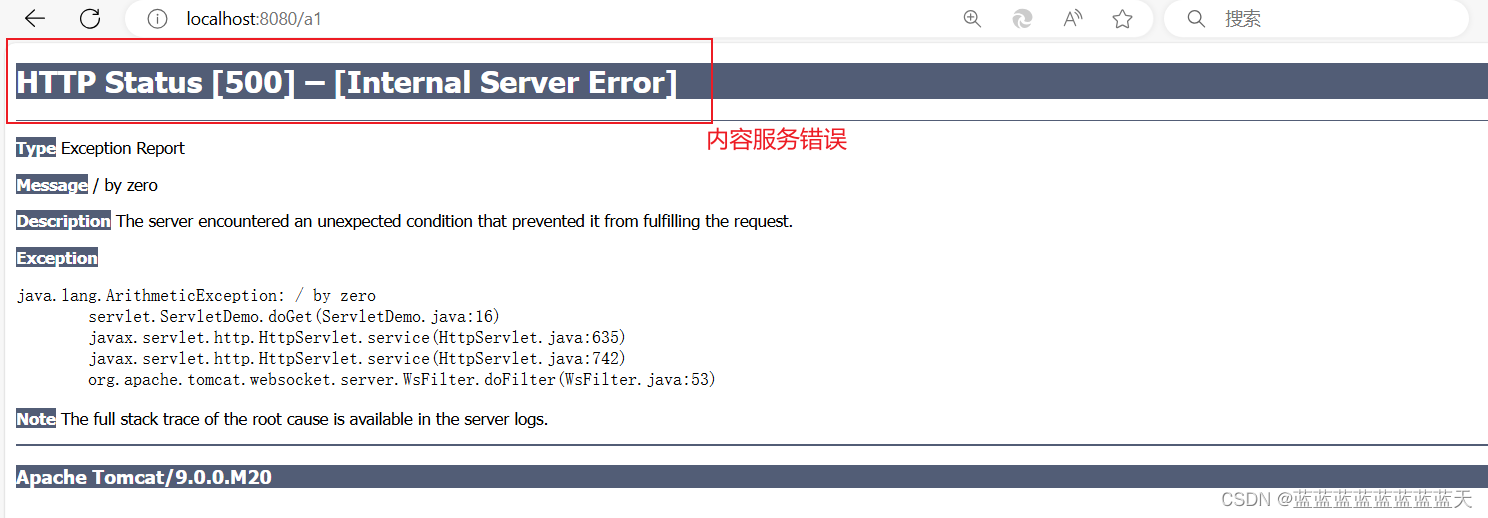
使用Servlet开发javaweb,请求常见错误详解及其解决办法【404、405、500】
Servlet报错的情况多种多样,涵盖了配置错误、代码逻辑错误、资源未找到、权限问题等多个方面。以下是一些常见的Servlet报错情况及其可能的原因和解决方法: 404 Not Found: 错误原因图示: URL映射 发送请求,出现404错误 原因: 请…...
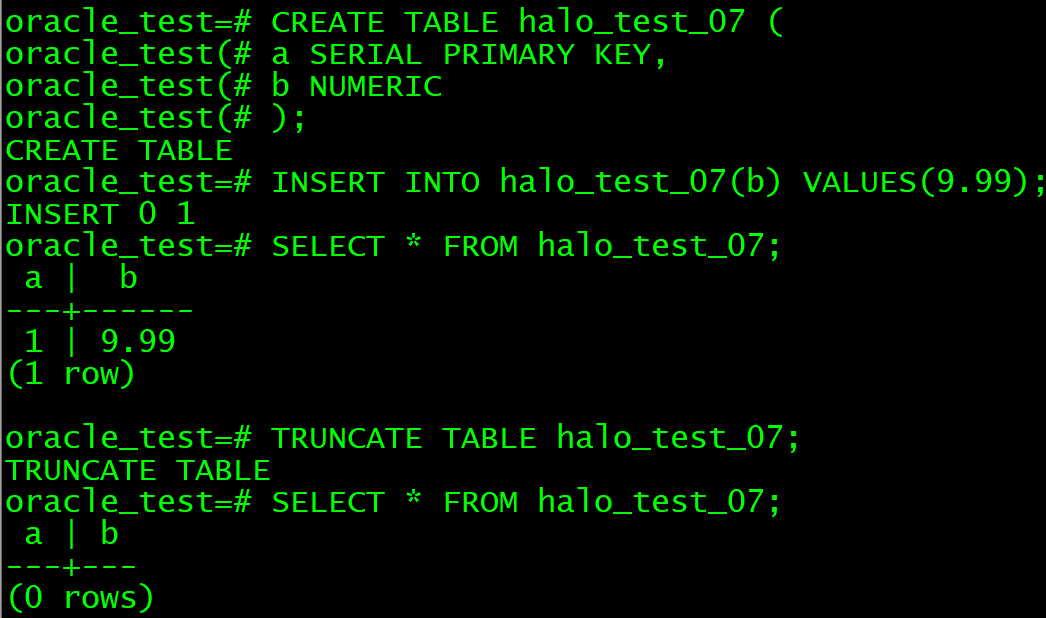
数据库管理-第210期 HaloDB-Oracle兼容性测试02(20240622)
数据库管理210期 2024-06-22 数据库管理-第210期 HaloDB-Oracle兼容性测试02(20240622)1 表增加列2 约束3 自增列4 虚拟列5 表注释6 truncat表总结 数据库管理-第210期 HaloDB-Oracle兼容性测试02(20240622) 作者:胖头…...

SpringBoot实现定时任务的动态停止和更新
目录 定时任务管理器定时任务的任务接口定时任务和定时任务结果的缓存对象定时任务使用姿势 定时任务管理器 负责启动一个定时任务、停止一个定时任务、更新一个定时任务 /*** 定时任务管理器* 1、创建并启动一个定时任务* 2、停止一个定时任务* 3、更新一个定时任务*/ publi…...

【threejs】火焰特效制作
2024-06-26 08-57-16火焰 shader 来源 //shadertory:https://www.shadertoy.com/view/ctVGD1//shadertory:https://www.shadertoy.com/view/ml3GWs 代码 import { DoubleSide, ShaderChunk, ShaderMaterial } from "three";export default fu…...

五原则四实践,REST API安全性请谨记
云原生和微服务架构等技术的流行让API受到越来越大的重视。那么当应用程序开始上云,各项需求都可以通过云服务满足的情况下,应用程序,尤其基于云端API的应用程序的安全问题该如何解决? 表现层状态转移(REST࿰…...
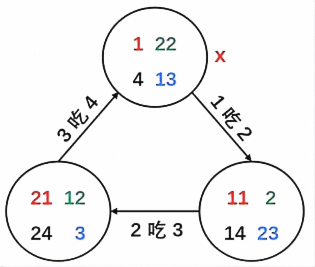
1390:食物链【NOI2001】
【解题思路】 并查集把三类动物划分成三个域,同类域(1-n)、捕食域〈n1-2n)、天敌域(2n1-3n)。把x放入同类域,xn放入其捕食域,x2n放入其天敌域。给在其他集合内安插两个“虚拟代表”…...

ICMAN液位检测——WS003B管道检测模组
ICMAN液位检测之WS003B管道检测模组 体积小,成本低, 液位检测精度高, 有水输出低电平无水高电平, 适用于饮水机、咖啡机、扫地机器人、洗地机等, 有需要朋友快联系我吧! AWE展会不容错过的ICMAN检测模组…...
YOLOv10使用教程及导读
首先推荐一下我的YOLOv8/v10项目,仅需一个v8的钱(69.9),付费进群,即可获取v8/v10的全部改进,欢迎进群。 1 YOLOv10简介 论文链接:https://arxiv.org/pdf/2405.14458 官方代码链接:ht…...

AIGC 在前端流式获取内容SSE
AIGC 在前端流式获取内容SSE 简介具体实现 简介 在 OpenAI 的 API 中,SSE 通常用于实现实时数据传输。例如,在聊天模型(如 ChatGPT)中,使用 SSE 可以让客户端实时接收到生成的对话内容,而不需要等待整个响…...

深度解析安全阀检测技术:方法与挑战
在工业生产中,安全阀作为防止压力容器和管道发生过压事故的关键部件,其性能和可靠性对于保证设备安全和人员安全具有重要意义。随着工业化进程的不断深入,对安全阀的检测和维护工作也日益受到重视。 接下来,佰德旨在探讨安全阀检…...
Dos)
网络安全--安全设备(一)Dos
安全设备--Dos 一、Dos 是什么二、DDos是什么三、Dos&DDos的区别四、产品防御Dos&DDos方式五、常见的DDoS攻击类型包括但不限于以下几种: 一、Dos 是什么 Dos(拒绝服务攻击,Denial-of-Service),是一种试图通过压倒网络或服务器来阻止合法用户访…...

<电力行业> - 《第3课:国家电网公司100条名词解释》
序号术语解 释1十不干一、无票的不干;二、工作任务、危险点不清楚的不干;三、危险点控制措施未落实的不干;四、超出作业范围未经审批的不干;五、未在接地保护范围内的不干;六、现场安全措施布置不到位、安全工器具不合…...

“论数据访问层设计技术及其应用”写作框架,系统架构设计师
论文真题 在信息系统的开发与建设中,分层设计是一种常见的架构设计方法,区分层次的目的是为了实现“高内聚低耦合”的思想。分层设计能有效简化系统复杂性,使设计结构清晰,便于提高复用能力和产品维护能力。一种常见的层次划分模…...
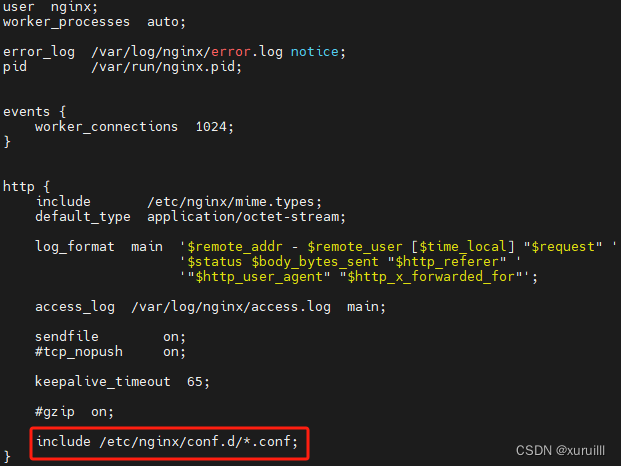
Docker部署前端,动态配置后端地址
本文介绍了使用Docker环境变量动态配置nginx。采用的是通过docker run -e xxxxxxx先往容器注入环境变量,然后进一步通过envsubst指令将环境变量写入到conf文件中,实现动态配置文件内容。 背景 前后端分离的架构下,经常会用到nginx反向代理来…...

k8s强制删除一个 Pod
在Kubernetes(K8s)中强制删除一个Pod,通常是因为Pod处于错误状态或无法正常终止。以下是强制删除Pod的步骤和相关信息: ### 步骤一:获取Pod的名称 首先,你需要知道要删除的Pod的名称。可以使用kubectl get …...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
