算法04 模拟算法之一维数组相关内容详解【C++实现】
大家好,我是bigbigli,模拟算法我们将分为几个章节来讲,今天我们只看一维数组相关的题目
目录
模拟的概念
训练:开关灯
解析
参考代码
训练:数组变化
解析
参考代码
训练:折叠游戏
解析
参考代码
模拟的概念
模拟算法就是模拟题目给的操作,用代码一步一步的描述出来即可。在过程中使用的都是我们已知的各种方法,如数组元素调用、排序、枚举等等,只是这些过程一般比较复杂。本次课程主要针对一维数组的模拟。
在各类算法竞赛中,包括CSP-J/S,NOIP等竞赛,经常会出现各类“模拟题目”,遇到这种题大家不需要害怕,甚至可以将其作为“送分题”,因为你只需要按照题目叙述的方式来写程序就能得到最终答案。模拟不是一种算法,而是一种技巧,要想掌握模拟题目,就需要多读题、多整理细节问题。
训练:开关灯
有n盏灯,从1到n按顺序依次编号,初始时所有灯都处于开启状态;有m个人,从1到m依次编号。
第一个人将灯全部关闭,第二个人将编号为2的倍数的灯打开,第三个人将编号为3的倍数的灯做相反处理(即将打开的灯关闭,将关闭的灯打开)。依照编号递增顺序,以后的人都一样,将凡是自己编号倍数的灯做相反处理。
请问:当第m个人操作之后,哪几盏灯是关闭的,按从小到大输出其编号,用逗号间隔。
【输入描述】一行,n和m,空格隔开
【输出描述】顺次输出关闭的灯的编号,用逗号隔开
【输入样例】10 1010
【输出样例】1,4,9
解析
因为灯只会出现0和1两种情况,我们可以使用数组元素来表示(类似桶),随后只需要重复m次,每次寻找当前序号的倍数为下标的元素进行更改,如果是1就变成0,是0就变成1。
最后对数组元素进行判断,找出是0的元素,就行数组元素下标的输出。
输出时要注意的问题是用逗号隔开不同于用空格隔开。
参考代码
#include<iostream>
using namespace std;
int a[1010];//全部是0,表示关闭
int main()
{int n,m;cin>>n>>m;for(int i=2;i<=m;i++)//从第二个人开始操作for(int j=i;j<=n;j+=i)//编号对应倍数下标if(a[j]==1) a[j]=0;else a[j]=1;//更改状态cout<<1;//1号肯定关闭for(int i=2;i<=n;i++)if(a[i]==0) cout<<","<<i;//间隔逗号输出return 0;
}
训练:数组变化
现有一个长度为n的数组,对这个数组进行m次操作,可以对数组进行的操作分为以下三类:
输入1 i: 表示输出数组中第i个元素的值;
输入2 i v: 表示在数组中第i个元素前加入新的元素v;
输入3 i: 表示删除数组中的第i个元素。
注意:三类操作都要满足 i <= n。
【输入描述】第1行:n,表示数组的初始长度
第2行:n个用空格间隔的数,表示原始的数组
第3行:m,表示操作的次数
接下来的m行分别是每次对数组进行的操作(题目描述中的三类操作中的一种)
【输出描述】对于第一种操作输出对应的答案,一行输出一个数。
【样例输入】
5
6 7 8 9 10
5
1 2
2 2 12
1 2
3 3
1 3
【样例输出】
7
12
8
解析
对题目的要求一步一步的实行,先保证数组的输入以后,需要对三种情况进行分类处理。第一种处理里面有输出,后面两种都是在操作。操作的要点是数组的插入和删除。插入的话,就要求插入位置后面所有数字向后移动一步,实现a[i+1]=a[i]的操作;而删除则需要当前位置后面所有的数字向前移动一步,实现a[i]=a[i+1]。这里需要注意移动的方向,要从头移动。
参考代码
#include<iostream>
using namespace std;
int a[1001];
int main()
{int n,m,p,q,v;cin>>n;for(int i=1;i<=n;i++)cin>>a[i];cin>>m;for(int i=0;i<m;i++){cin>>p;if(p==1){cin>>q;cout<<a[q]<<endl;}else if(p==2){cin>>q>>v;for(int j=n;j>=q;j--)//挨个向后移动a[j+1]=a[j];a[q]=v;//单独把插入的数字放入位置n++; //数组长度加1}else if(p==3){cin>>q;for(int j=q;j<n;j++)//挨个向前移动a[j]=a[j+1];n--;//数组长度减1}}return 0;
}
训练:折叠游戏
小明和小华在玩数组折叠游戏,游戏规则是,给出n个整数,按照从左到右的顺序排列,现在需要将这列整数从中间折叠m次,右边的叠加到左边,每次折叠后,重合的两个数字会相加变成一个新的数字。请你输出折叠m次后的s数组。
【输入描述】第1行:输入一个整数n表示序列的长度,输入一个整数m表示折叠的次数。
第2行:输入n个空格隔开的整数,整数不超过100。
【输出描述】输出折叠m次后的数组。
【输入样例】
5 2
1 2 3 4 5
【输出样例】
9 6
解析
数组对折,需要把后半部分移动到前半部分对应位置进行数组相加,所以移动次数为n/2(即循环次数)。
然后需要进行的就是数组加法。
最后要对数组长度也做n/2的操作。
但是这里需要注意的是,如果长度是奇数不能只是简单的n/2哦。
参考代码
#include<iostream>
using namespace std;
int a[10010];
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=m;i++){for(int j=1;j<=n/2;j++)a[j]+=a[n-j+1];if(n%2!=0)n++;n/=2;}for(int i=1;i<=n;i++)cout<<a[i]<<' ';return 0;
}从入门到算法,再到数据结构,查看全部文章请点击此处![]() http://www.bigbigli.com/
http://www.bigbigli.com/
相关文章:
算法04 模拟算法之一维数组相关内容详解【C++实现】
大家好,我是bigbigli,模拟算法我们将分为几个章节来讲,今天我们只看一维数组相关的题目 目录 模拟的概念 训练:开关灯 解析 参考代码 训练:数组变化 解析 参考代码 训练:折叠游戏 解析 参考代码 …...

【技术解码】百数SRM:如何助力企业快速优化供应链管理?
SRM应用是企业优化供应链管理的重要工具,它帮助企业全面管理供应商关系,从评估、选择到协同合作和绩效监控,确保供应链的稳定性和效率。 对于企业来说,通过全面管理供应商关系,可以降低采购风险,提升产品质…...

想要用tween实现相机的移动,three.js渲染的canvas画布上相机位置一点没动,如何解决??
🏆本文收录于「Bug调优」专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收藏&&…...
SQL连接与筛选:解析left join on和where的区别及典型案例分析
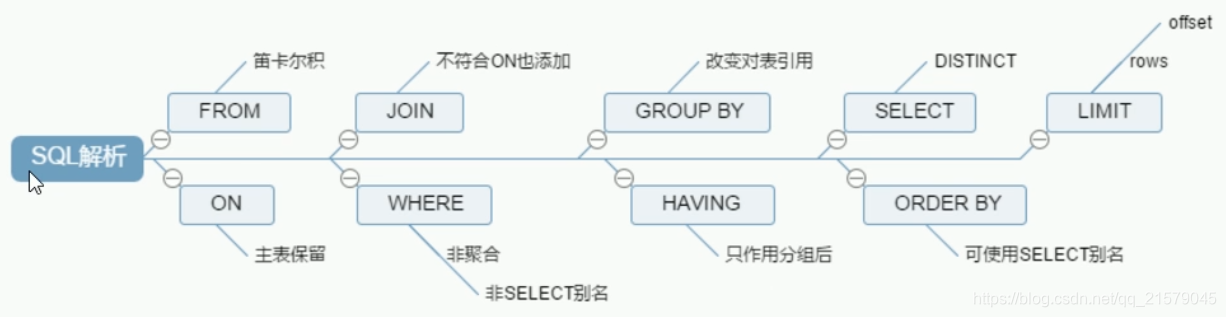
文章目录 前言数据库在运行时的执行顺序一、left join on和where条件的定义和作用left join on条件where条件 二、left join on和where条件的区别原理不同left join原理:where原理: 应用场景不同执行顺序不同(作用阶段不同)结果集…...

oliva-bruteforce-luks
olivaeasyLUKS v2破解、bruteforce-luks工具使用、cryptsetup使用、cap_dac_read_searcheip、mysql使用 主机发现 ┌──(kali㉿kali)-[~/桌面/OSCP] └─$ sudo netdiscover -i eth0 -r 192.168.44.148/24服务扫描 ┌──(kali㉿kali)-[~/桌面/OSCP] └─$ sudo nmap -sV -…...
图像超分辨率重建
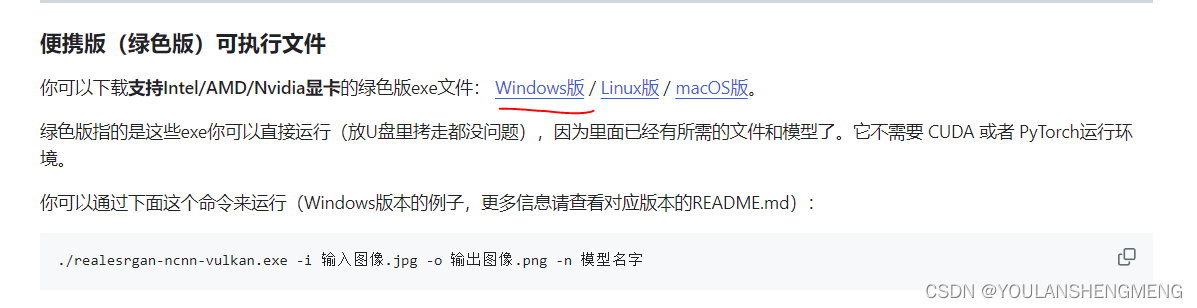
一、什么是图像超分辨 图像超分辨是一种技术,旨在通过硬件或软件的方法提高原有图像的分辨率。这一过程涉及从一系列低分辨率的图像中获取一幅高分辨率的图像,实现了时间分辨率向空间分辨率的转换。超分辨率重建的核心思想是利用多帧图像序列的时间带宽来…...

小米上架遇到的隐私协议问题
1. 找到【APP权限设置】,点击详情,一一对照,删除没用的,新增小米商家必须要有的内容 2. APP 存在未经用户同意读取“OAID”的行为 uniapp官方文档对应内容处...

【区分vue2和vue3下的element UI Message 消息提示组件,分别详细介绍属性,事件,方法如何使用,并举例】
在 Vue 2 中,我们通常使用 Element UI 的 this.$message 方法来显示消息提示,而不是作为一个组件直接在模板中使用。然而,在 Vue 3 的 Element Plus 中,虽然 this.$message 的使用方式仍然保留,但官方文档可能更倾向于…...

架构设计 - Nginx Lua 缓存配置
摘要: web 应用业务缓存通常3级: 一级缓存:JVM 本地缓存 二级缓存:Redis集中式缓存 三级缓存:Nginx Proxy Cache 缓存 或 Nginx Lua 缓存 四级缓存:静态资源CDN缓存 页面静态化 本文主要分享 Nginx Lua 缓存配置开发 鉴于 Nginx Proxy Cache 缓存的劣势,在生产项目…...

lua的GC
关于lua的gc云风大佬在 Lua GC 的源码剖析 系列文章中讲得很清楚,这里做一下简单的记录。 分步gc lua使用的是一种三色标记清除算法(tri-color incremental mark & sweep),大体步骤如下: 初始阶段,所…...

基于python爬虫对豆瓣影评分析系统的设计与实现
基于python爬虫对豆瓣影评分析系统的设计与实现 Design and Implementation of a Python-based Web Crawler for Analyzing Douban Movie Reviews 完整下载链接:基于python爬虫对豆瓣影评分析系统的设计与实现 文章目录 基于python爬虫对豆瓣影评分析系统的设计与实现摘要第一…...

想让梦想照进现实?六西格玛绿带培训为你架起桥梁
六西格玛,这个源自摩托罗拉的质量管理方法论,如今已成为全球众多企业追求卓越的秘诀。它强调以数据为基础,通过减少变异和浪费,提高流程效率和质量,进而提升企业整体绩效。而六西格玛绿带培训,则是这个强大…...

大数据面试题之HDFS
目录 HDFS文件写入和读取流程 HDFS组成架构 介绍下HDFS,说下HDFS优缺点,以及使用场景 HDFS作用 HDFS的容错机制 HDFS的存储机制 HDFS的副本机制 HDFS的常见数据格式,列式存储格式和行存储格式异同点,列式存储优点有哪些? …...

(9)农作物喷雾器
文章目录 前言 1 必要的硬件 2 启用喷雾器 3 配置水泵 4 参数说明 前言 Copter 包括对农作物喷雾器的支持。该功能允许自动驾驶仪连接到一个 PWM 操作的泵和(可选)旋转器,根据飞行器速度控制液体肥料的流动速度。 稍微过时的视频显示了…...

智慧互联:Vatee万腾平台展现科技魅力
随着科技的迅猛发展,我们的生活正逐渐变得智能化、互联化。在这个信息爆炸的时代,一个名为Vatee万腾的平台正以其独特的魅力,引领我们走向一个更加智能的未来。 Vatee万腾,这个名字本身就充满了对科技未来的憧憬与期待。作为一家专…...
Charles抓包工具系列文章(四)-- Rewrite 重写工具
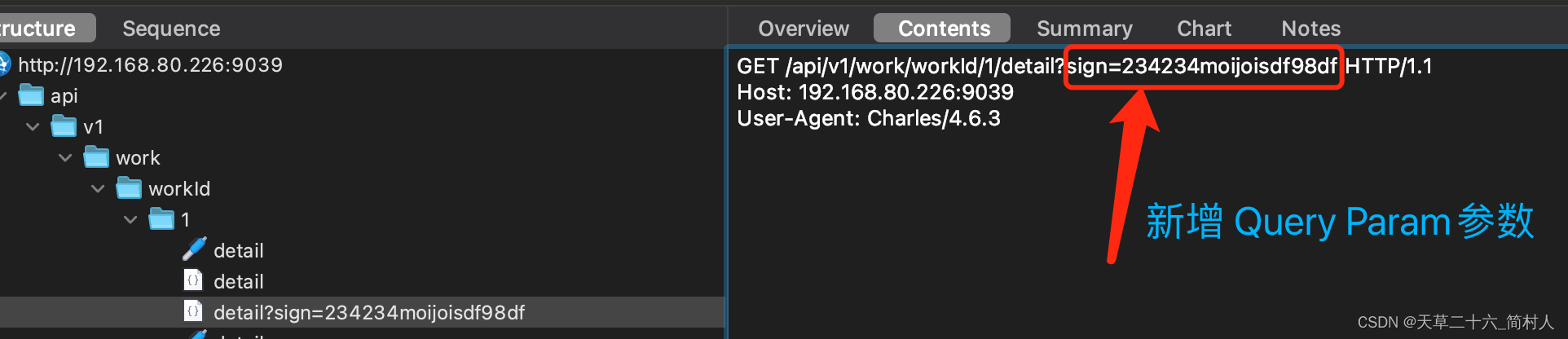
一、背景 这是一款比Map Local/Remote 还强大的工具,更加灵活,体现在以下几点: 重写request报文重写response报文header 字段的增删改query param 字段的增删改重写 body 字段改写http 响应状态status重写host/url/path 从这也可以看出其强…...
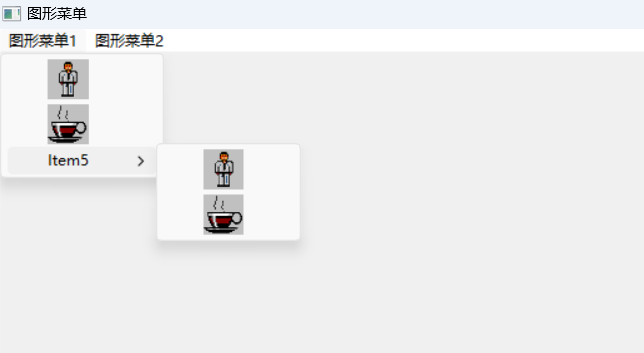
【PB案例学习笔记】-24创建一个窗口图形菜单
写在前面 这是PB案例学习笔记系列文章的第24篇,该系列文章适合具有一定PB基础的读者。 通过一个个由浅入深的编程实战案例学习,提高编程技巧,以保证小伙伴们能应付公司的各种开发需求。 文章中设计到的源码,小凡都上传到了gite…...

环境配置的相关问题
一、shap安装踩坑 遇到错误: A module that was compiled using NumPy 1.x cannot be run in NumPy 2.0.0 as it may crash. To support both 1.x and 2.x versions of NumPy, modules must be compiled with NumPy 2.0. Some module may need to rebuild instead…...

github配置可拉取项目到本地
首先配置用户名和邮箱: git config --global user.name 自己的名字git config --global user.email 自己的邮箱配置完之后检查一下: git config --global user.namegit config --global user.email如果提示的是自己配置好的名字和邮箱就Ok 然后拉取githu…...

Snippet-AndroidFontWeight
常用FontWeight值 <?xml version"1.0" encoding"utf-8"?> <resources><integer name"font_weight_Thin">100</integer><integer name"font_weight_ExtraLight">200</integer><integer name…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...
