扩展欧几里得算法及其应用
前言
由于数论的板子真的很抽象,也很难背,所以特此记录扩展欧几里得算法的板子和它的用途
本篇文章只涉及应用,不涉及证明,如需理解证明还请各位移步其他优秀的讲解!
扩展欧几里得算法
先粘一下板子的代码
typedef long long LL ; LL exgcd(LL a, LL b, LL &x, LL &y) {if (!b) {x = 1, y = 0 ; return a ; }LL d = exgcd(b, a % b, y, x) ; y -= a / b * x ; return d ; }
变量解释
对于方程:ax + by = d
其中 a 和 b 都是常数 (已知量),d 是 a 和 b 的最大公约数
x 和 y 是我们希望求得的一组满足方程的解
应用例题

题目链接🔗:222. 青蛙的约会 - AcWing题库
题目分析

AC代码
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std ;typedef long long LL ; LL exgcd(LL a, LL b, LL &x, LL &y)
{if (!b) {x = 1, y = 0 ; return a ; }LL d = exgcd(b, a % b, y, x) ; y -= a / b * x ; return d ;
}int main()
{ios::sync_with_stdio(false) ; LL a, b, m, n, L ; cin >> a >> b >> m >> n >> L ;LL x, y ; LL d = exgcd(m - n, L, x, y) ; if ((b - a) % d) cout << "Impossible" << endl ;else {x *= (b - a) / d ; LL t = abs(L / d) ; cout << (x % t + t) % t << endl ; // 求最小正整数解}return 0 ;
}难点解释
为什么要计算 t ?
解释:
题解来源🔗: AcWing 222. 青蛙的约会 - AcWing
再来一道题目巩固一下
同余方程模版题 🔗203. 同余方程 - AcWing题库
题目描述

题目分析
a * x % b = 1 等价于找到两个数 x 和 y 使得 a * x + b * y = 1
这恰好是我们扩展欧几里得算法的基本解决对象,直接套板子就行了,由于题目保证输入一定有解,所以我们可以认为 a 和 b 是互质的,因此可以使用扩展欧几里得算法。
最后记得对b取模保证答案为最小正数。
AC代码
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std ;typedef long long LL ; int exgcd(int a, int b, int &x, int &y)
{if (!b) {x = 1, y = 0 ; return a ; }int d = exgcd(b, a % b, y, x) ; y -= a / b * x ; return d ;
}int main()
{ios::sync_with_stdio(false) ; int a, b ; cin >> a >> b ; int x, y ; exgcd(a, b, x, y) ; cout << (x % b + (LL)b) % b << endl ; return 0 ;
}END
相关文章:

扩展欧几里得算法及其应用
前言 由于数论的板子真的很抽象,也很难背,所以特此记录扩展欧几里得算法的板子和它的用途 本篇文章只涉及应用,不涉及证明,如需理解证明还请各位移步其他优秀的讲解! 扩展欧几里得算法 先粘一下板子的代码 typedef lo…...

JAVA练习75-全排列
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 提示:这里可以添加本文要记录的大概内容: 3月11日练习内容 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目-…...
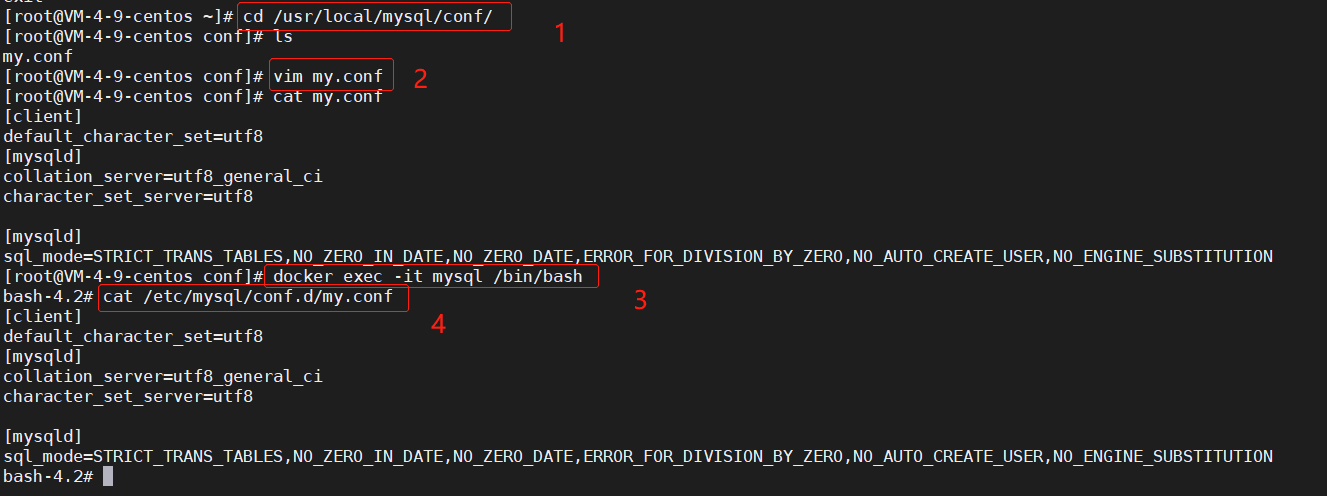
Linux下Docker安装mysql-超详细步骤
安装Docker Engine官方参考文档:https://docs.docker.com/engine/install/centos/若之前有安装docker,需要先卸载之前的dockersudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \d…...

弹性存储-对象存储OSS部分
对象存储介绍 对象存储(object storage service,简称oss),具备与平台无关的rest api接口,可提供99.9999999999%(12个9)的数据持久性和99.995%的数据可用性。 OSS优势 功能介绍 存储空间bucke…...

强推!30个遥感数据下载网站整理分享
1、中国遥感数据共享网(http://rs.ceode.ac.cn/)国内存档周期最长的数据网站,对Landsat数据免费共享,也可订购国外商业卫星数据。注册账号,通过审核就可直接下载。2、中国资源卫星应用中心(https://data.cr…...
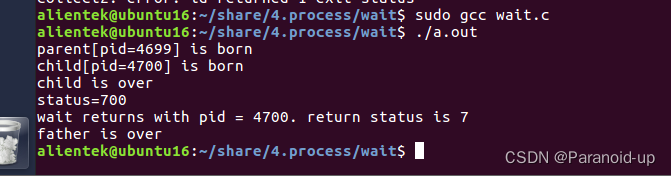
进程系统调用
进程系统调用 文章目录进程系统调用fork()进程创建:fock()fork函数fork用法僵尸进程孤儿进程vfork函数vfork与fork区别exec函数族exec函数族-何时使用?exec函数族语法exec函数族使用区别exit和_exit_exit和exit的区别wait和waitpidfork() 进程创建&…...

dubbo进阶——服务导出
服务导出 在这里记录一下对" Dubbo 导出服务的过程"的研究。 触发时机 public class ServiceBean<T> extends ServiceConfig<T> implements InitializingBean, DisposableBean, ApplicationContextAware, ApplicationListener<ContextRefreshedEv…...

【竞品分析】如何撰写竞品分析?竞品分析的基本结构?以及优秀的竞品分析案例
文章目录一、撰写竞品分析的意义二、撰写的节点三、竞品分析内容的基本结构四、总结本文对视频 如何撰写竞品分析(demo)进行了总结。一、撰写竞品分析的意义 竞品分析是指对现有的或潜在的竞争产品的优势和劣势进行评价。现在被广泛应用于互联网产品的…...

海思ubootsd卡协议
在start_armboot()函数中调用mmc_initialize(0)初始化mmc;最终调用到int hi_mci_initialize(unsigned int dev_num)函数;内容如下:static int hi_mci_initialize(unsigned int dev_num) {struct mmc *mmc NULL;static struct himci_host *host;unsigned int regval;unsigned l…...

nuxt3使用总结
目录 背景 安装 项目配置 路由 Tailwindcss引入 全局样式配置 css预处理器 安装 Tailwindcss 项目的配置 部署上线 seo优化 背景 新入职了一家公司,刚进入公司第一个需求就是先做一个公司的官网,需要使用vue写,作为祖师爷的粉丝…...

指向函数的指针详解,以及如何使用指向函数的指针变量做函数参数
指向函数的指针作为函数参数,是 C 语言实际应用中的一个比较深入的部分。 目录 一、什么是函数的指针 二、用函数指着变量调用函数 2.1举例说明 三、怎样定义和使用指向函数的指针变量 3.1定义指向函数的指针变量 3.2指向函数的指针变量详解 3.3通过指针变量…...
Spring——spring整合JUnit
JUnit定义: Junit测试是程序员测试,即所谓 白盒测试 ,因为程序员知道被测试的软件如何(How)完成功能和完成什么样(What)的功能。 Junit是一套框架,继承TestCase类,就可以用Junit进行…...

保障信息安全:使用PyZbar库识别二维码图片可以快速获取二维码中的信息,保障信息安全。
目录 简介: 源代码: 源代码说明: 效果如下所示: 简介: 不用摄像头识别二维码可以应用在以下场景: 批量处理二维码图片:可以在服务器上使用PyZbar等库来批量处理二维码图片,例如读…...

从LeNet到ResNet:深入探索卷积神经网络
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
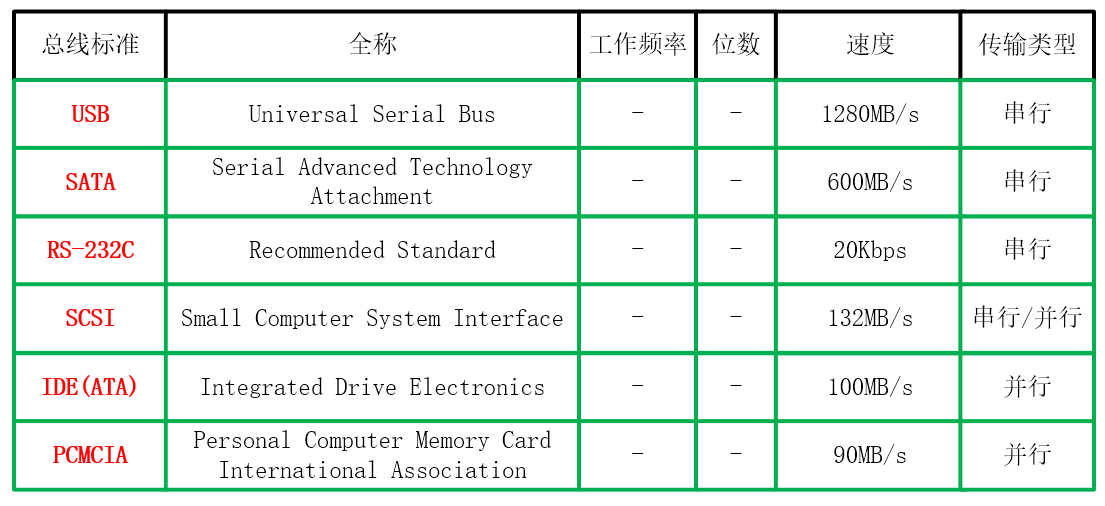
计算机组成原理_总线标准
计算机组成原理总目录总线标准 总线标准是系统与各模块、模块与模块之间的一个互连的标准,就像我们用汉语来相互交流一样。 1. 系统总线 ISA总线的扩展插槽,其颜色一般为黑色,比PCI接口插槽要长些,位于主板的最下端。 可插接显卡&…...

蓝桥杯C/C++VIP试题每日一练之芯片测试
💛作者主页:静Yu 🧡简介:CSDN全栈优质创作者、华为云享专家、阿里云社区博客专家,前端知识交流社区创建者 💛社区地址:前端知识交流社区 🧡博主的个人博客:静Yu的个人博客 🧡博主的个人笔记本:前端面试题 个人笔记本只记录前端领域的面试题目,项目总结,面试技…...

树莓派测试wifi与eth速率
测试网速方法: 1.安装插件: 首先在树莓派端安装iperf3 sudo apt install iperf3PC端也需要安装iperf3,单击下面网址即可 下载网址 压缩包解压到桌面,文件内容如下图所示: 2.开始测速服务: 树莓派端在…...

关系抽取方面的基础
关系抽取方面的基础一、基本概念1. 什么是关系抽取(Relation Extraction,RE)?2. 都有什么奇怪的关系?3. 任务评价指标二、 关系抽取方法2.1 按模型结构分——Pipeline 和 Joint方法Pipeline方法Joint方法2.2 按解码方式…...
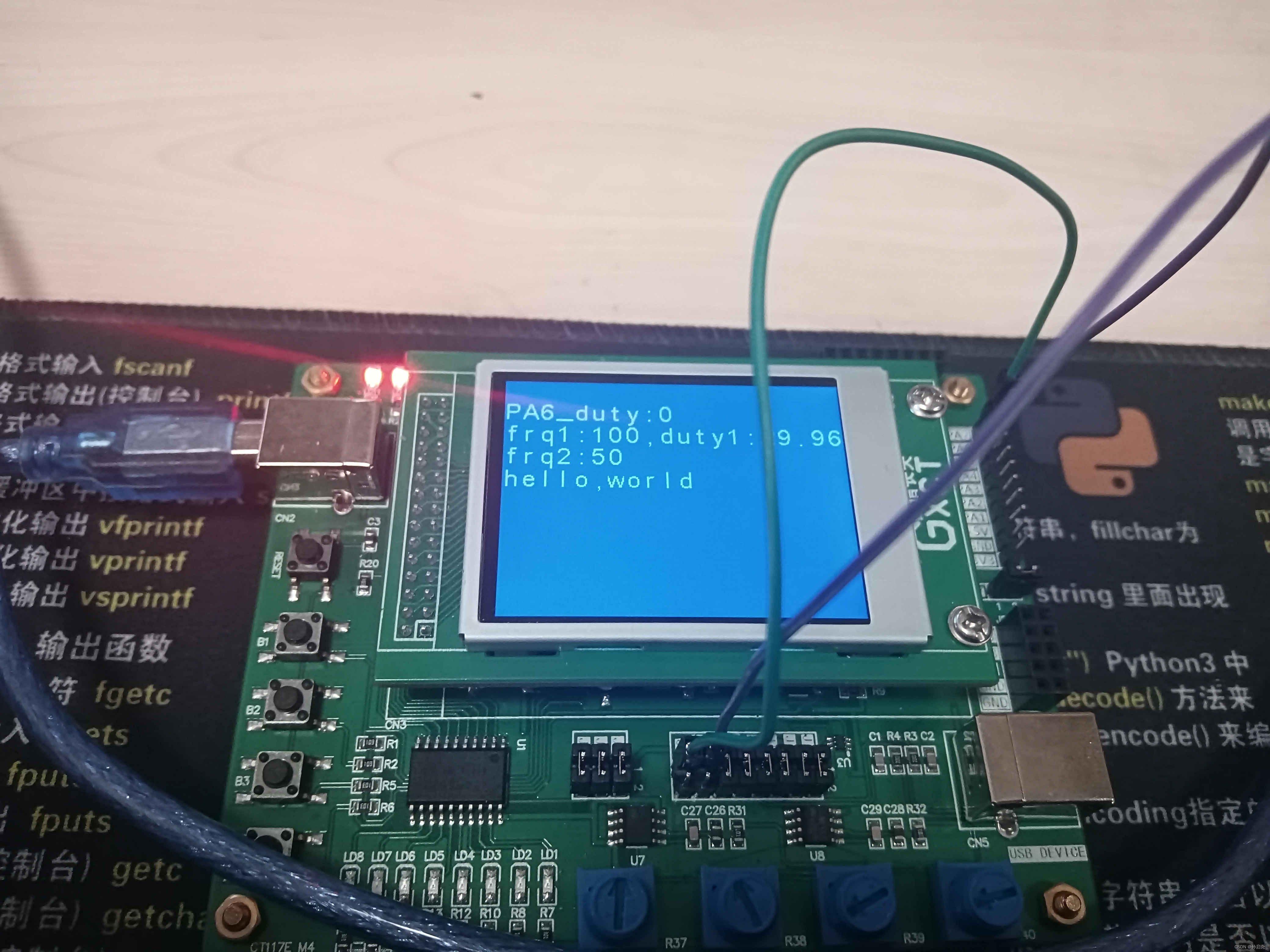
蓝桥杯嵌入式(G4系列):定时器捕获
前言: 定时器的三大功能还剩下最后一个捕获,而这在蓝桥杯嵌入式开发板上也有555定时器可以作为信号发生器供定时器来测量。 原理图部分: 开发板上集成了两个555定时器,一个通过跳线帽跟PA15相连,最终接到了旋钮R40上&…...
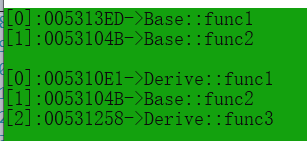
多态的定义、重写、原理
多态 文章目录多态多态的定义和条件协变(父类和子类的返回值类型不同)函数隐藏和虚函数重写的比较析构函数的重写关键字final和override抽象类多态的原理单继承和多继承的虚函数表单继承下的虚函数表多继承下的虚函数表多态的定义和条件 定义࿱…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

