240626_昇思学习打卡-Day8-稀疏矩阵
240626_昇思学习打卡-Day8-稀疏矩阵
稀疏矩阵
在一些应用场景中,比如训练二值化图像分割时,图像的特征是稀疏的,使用一堆0和极个别的1表示这些特征即费事又难看,此时就可以使用稀疏矩阵。通过参考大佬博文,结合个人理解,记录如下:
CSR(Compressed Sparse Row Format)
CSR矩阵通过使用三个一维数组来存储矩阵,row,column和value(各作者可能叫法不同,实际意义相同)
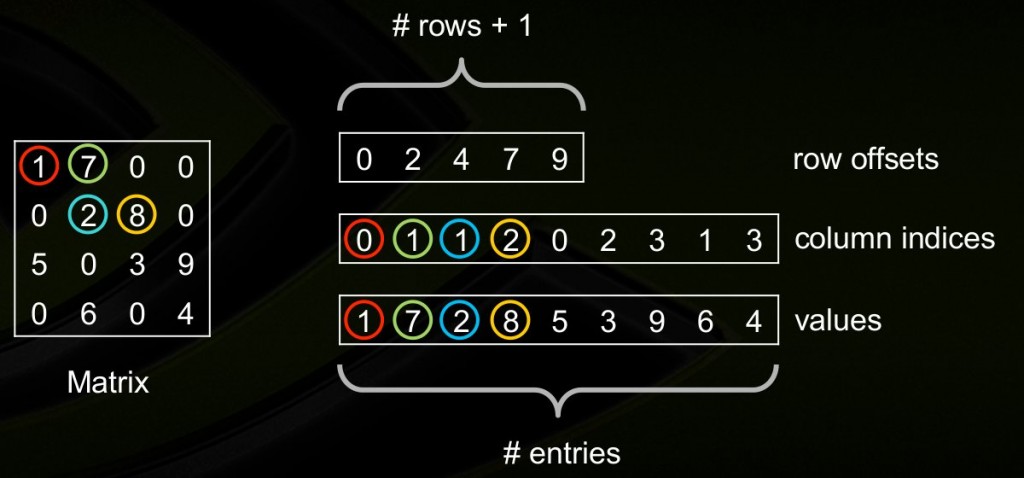
假如我们有一个稀疏矩阵
[ 1 7 0 0 0 2 8 0 5 0 3 9 0 6 0 4 ] \left[ \begin{matrix} 1 & 7 & 0 & 0 \\ 0 & 2 & 8 & 0 \\ 5 & 0 & 3 & 9 \\ 0 & 6 & 0 & 4 \\ \end{matrix} \right] 1050720608300094
此时我们可以轻易地看出
value=([1,7,2,8,5,3,9,6,4]) # 里面所有的非零项,从左往右从上往下拿出来
shape=(4,4)
对于row和column来说就比较难看了,相对来说column较简单,column就是每一个非零数对应的列数,我们对照着value来看:
对value的第一个值1,他在稀疏矩阵中第一行第一列,换成索引就是0行0列,此时他在column中的值就是0(列)
对value的第二个值7,他在稀疏矩阵中第一行第二列,换成索引就是0行1列,此时他在column中的值就是1(列)
对value的第三个值2,他在稀疏矩阵中第二行第二列,换成索引就是1行1列,此时他在column中的值就是1(列)
对value的第四个值8,他在稀疏矩阵中第二行第三列,换成索引就是1行2列,此时他在column中的值就是2(列)
对value的第五个值5,他在稀疏矩阵中第三行第一列,换成索引就是2行0列,此时他在column中的值就是0(列)
对value的第六个值3,他在稀疏矩阵中第三行第三列,换成索引就是2行2列,此时他在column中的值就是2(列)
对value的第七个值9,他在稀疏矩阵中第三行第四列,换成索引就是2行3列,此时他在column中的值就是3(列)
对value的第八个值6,他在稀疏矩阵中第四行第二列,换成索引就是3行1列,此时他在column中的值就是1(列)
对value的第九个值4,他在稀疏矩阵中第四行第四列,换成索引就是3行3列,此时他在column中的值就是3(列)
所以得到column的值为
column=([0,1,1,2,0,2,3,1,3])
然后让我们来关注row的值,row的长度是原张量的行数+1,比如此处原张量为4行,所以我们row的长度就是5,row的定义为每一行的第一个非零元素在value中的位置,这也才4个数,所以还要再加一个,value的总长度,说的比较抽象,以下举例说明:
首先第一行,第一行的第一个非零元素1,在value中位于第一个,转换成索引就是0,所以第一行在row中的值就是0。
其次第二行,第二行的第一个非零元素2,在value中位于第三个,转换成索引就是2,所以第二行在row中的值就是2。
其次第三行,第三行的第一个非零元素5,在value中位于第五个,转换成索引就是4,所以第三行在row中的值就是4。
其次第四行,第四行的第一个非零元素6,在value中位于第八个,转换成索引就是7,所以第四行在row中的值就是7。
其次第五行,欸等等,第五行在哪呢。没有的啦,row中第五个元素就是value的总长度啦,所以第五个值就是9。
所以row的值就出来咯
row=([0,2,4,7,9])
COOTensor
相对较为简单,仅存储非零元素及每个非零元素的坐标,可视化较强,也是通过使用三个一维数组来存储矩阵,row,column和value
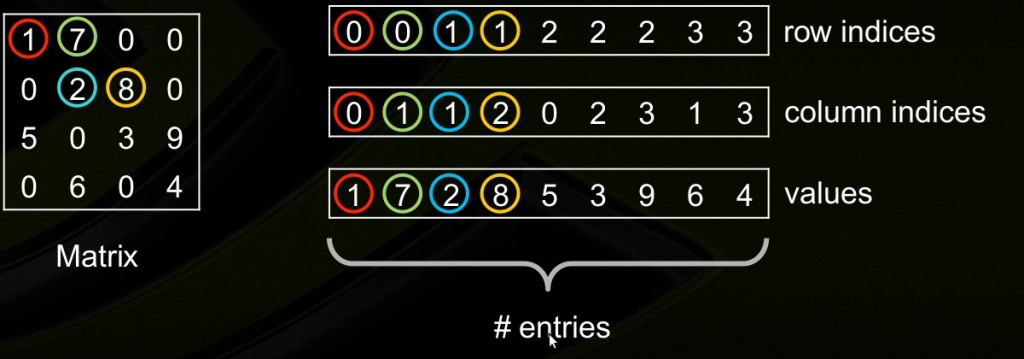
对于一个稀疏矩阵
[ 1 7 0 0 0 2 8 0 5 0 3 9 0 6 0 4 ] \left[ \begin{matrix} 1 & 7 & 0 & 0 \\ 0 & 2 & 8 & 0 \\ 5 & 0 & 3 & 9 \\ 0 & 6 & 0 & 4 \\ \end{matrix} \right] 1050720608300094
value、shape、column值都和CSR矩阵相同:
value=([1,7,2,8,5,3,9,6,4]) # 里面所有的非零项,从左往右从上往下拿出来
shape=(4,4)
column=([0,1,1,2,0,2,3,1,3])
row有所不同,此时的row代表的是每一个非零元素在第几行,比如:
第一个非零元素1在第一行,行索引为0,所以该元素对应的row值为0。
第二个非零元素7在第一行,行索引为0,所以该元素对应的row值为0。
第三个非零元素2在第二行,行索引为1,所以该元素对应的row值为1。
第四个非零元素8在第二行,行索引为1,所以该元素对应的row值为1。
第五个非零元素5在第三行,行索引为2,所以该元素对应的row值为2。
第六个非零元素3在第三行,行索引为2,所以该元素对应的row值为2。
第七个非零元素9在第三行,行索引为2,所以该元素对应的row值为2。
第八个非零元素6在第四行,行索引为3,所以该元素对应的row值为3。
第九个非零元素4在第四行,行索引为3,所以该元素对应的row值为3。
所以该矩阵的row为
row=([0,0,1,1,2,2,2,3,3])
参考博客:
稀疏矩阵的存储格式 | Xiang的博客 (flyxu.github.io)
打卡图片:
相关文章:

240626_昇思学习打卡-Day8-稀疏矩阵
240626_昇思学习打卡-Day8-稀疏矩阵 稀疏矩阵 在一些应用场景中,比如训练二值化图像分割时,图像的特征是稀疏的,使用一堆0和极个别的1表示这些特征即费事又难看,此时就可以使用稀疏矩阵。通过参考大佬博文,结合个人理…...

Docker: 使用容器化数据库
使用容器化数据库 使用本地容器化数据库提供了灵活性和简易的设置,使您能够在不需要传统数据库安装开销的情况下,紧密模拟生产环境。Docker 简化了这一过程,只需几条命令就可以在隔离的容器中部署、管理和扩展数据库。 在本指南中,您将学习如何: 运行本地容器化数据库访…...

Oracle对用户敏感数据进行编码处理
由于系统运行时间比较长,没有对用户的身份证号、邮箱、手机号进行脱敏处理,后期对数据进行了编码。 更新表数据 sql UPDATE sys_staff SET MOBIL_PHONE CASEWHEN MOBIL_PHONE IS NULL THEN ELSE utl_raw.cast_to_varchar2(utl_encode.base64_encode(ut…...

VXLAN详解:概念、架构、原理、搭建过程、常用命令与实战案例
一、VXLAN概述 1.1 VXLAN的定义 VXLAN(Virtual Extensible LAN,虚拟可扩展局域网)是一种网络虚拟化技术,通过在现有IP网络上创建虚拟网络,使数据中心可以实现大规模的网络隔离和扩展。VXLAN使用MAC-in-UDP封装技术&a…...

Redis-数据类型-Hash
文章目录 1、查看redis是否启动2、通过客户端连接redis3、切换到db3数据库4、插入新数据返回15、获取指定哈希(hash)对象的所有字段(field)名6、获取存储在指定哈希(hash)对象中的所有字段(fiel…...
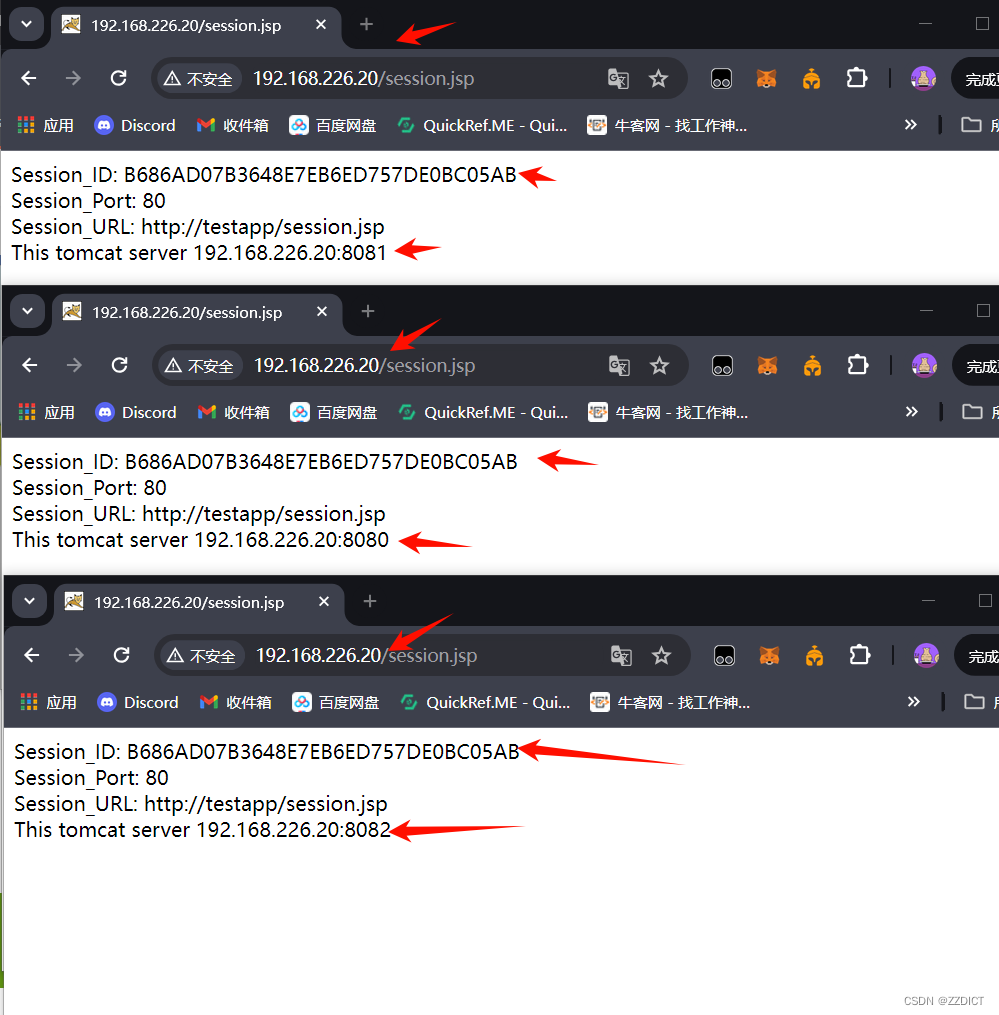
基于redisson实现tomcat集群session共享
目录 1、环境 2、修改server.xml 3、修改context.xml 4、新增redisson配置文件 5、下载并复制2个Jar包到Tomcat Lib目录中 6、 安装redis 7、配置nginx负载均衡 8、配置测试页面 9、session共享测试验证 前言: 上篇中,Tomcat session复制及ses…...
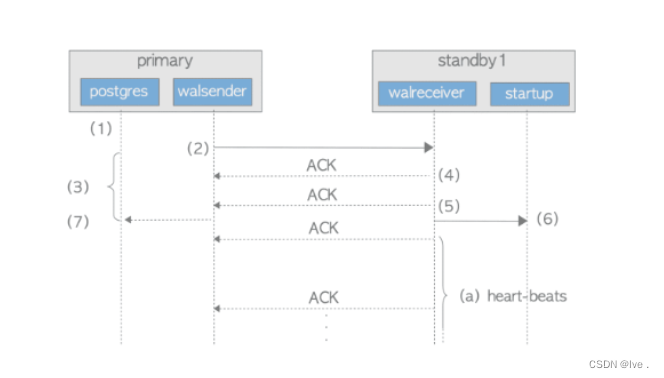
postgres数据库的流复制
1. 流复制和逻辑复制的差异 逻辑复制和流复制最直观的不同是,逻辑复制支持表级别复制区分点事原理不同 逻辑日志是在wal日志产生的数据库上,由逻辑解析模块对wal日志进行初步的解析,解析结果是ReorderBufferChange(理解为HeapTup…...

Dxf库中的DL_Extrusion类
类DL_Extrusion DL_Extrusion 是 DXF 库中的一个类,用于表示三维实体的扩展信息。在 DXF 文件中,DL_Extrusion 类通常用于表示具有高度的三维图形实体,如立方体、圆柱体等,以及其它具有体积的几何对象。 以下是一个简单的示例代…...
“ONLYOFFICE 8.1版本评测:功能更强大,用户体验更佳”
最新版本的在线编辑器已经发布 ONLYOFFICE在线编辑器的最新版本8.1已经发布,整个套件带来了30多个新功能和432个bug修复。这个强大的文档编辑器支持处理文本文档、电子表格、演示文稿、可填写的表单和PDF,并允许多人在线协作,同时支持AI集成…...

搜维尔科技:【研究】触觉手套比控制器更能带来身临其境、更安全、更高效的虚拟体验
自然交互可提高VR模拟的有效性。研究表明,触觉手套比控制器更能带来身临其境、更安全、更高效的虚拟体验。 以下是验证 医疗培训中的触觉技术 “ 95.5%的参与者表示触摸是 XR 教育的重要组成部分,90.9% 的参与者表示 XR 触觉将提供一个安全的学习场所。…...

【小学期】实体类设计——以学生管理系统为例
项目目录中的位置 将Student.java文件放在src/model目录中,即: student_management │ ├── src │ ├── model │ │ ├── Student.java // 这里是Student实体类 │ │ └── StudentDAO.java │ │ │ ├── view │ │ …...

Java测试类
在Java中,为了编写测试类,通常使用JUnit框架。 1. 首先,创建一个名为Calculator的简单Java类,它包含一个方法add用于计算两个整数的和: public class Calculator {public int add(int a, int b) {return a b;} } 2.…...

python 中面向对象编程:深入理解封装、继承和多态
在本章中,我们将深入探讨Python中的高级面向对象编程概念,包括封装、继承和多态。让我们开始吧! 目录 面向对象简介类和实例属性和方法继承和多态 高级面向对象概念私有变量使用 property使用 __slots__类的特殊成员__doc____call____str____…...

OpenCV练习(2)图像校正
1、傅里叶变换 霍夫变换 直线 角度 旋转2、边缘检测 霍夫变换 直线角度 旋转3、四点透视 角度 旋转4、检测矩形轮廓 角度 旋转 1.目的 实现类似全能扫面王的图像校正功能 2. 基于轮廓提取和透射变换 基于轮廓提取和透射变换的矫正算法更适用于车牌、身份证、人民…...

Excel中的“点选输入”——次级下拉列表创建
在Excel中,用“数据验证”功能可以设置下拉列表,二级下拉列表需要设置公式。 (笔记模板由python脚本于2024年06月16日 18:36:37创建,本篇笔记适合经常使用Excel处理数据的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:http…...

基于 Spring AOP 实现安全检查
在现代应用程序中,安全性是一个至关重要的方面。通过对系统中的关键操作进行安全检查,可以有效防止未授权的访问和操作。Spring AOP(面向切面编程)提供了一种优雅的方式来实现安全检查,而无需修改业务逻辑代码。本文将…...

【MySQL】数据库事务详解
文章目录 前言1. 事务的定义2. 事务的四个特性2.1 原子性2.2 一致性2.3 隔离性2.4 持久性 3. 事务的并发问题3.1 脏读3.2 不可重复读3.3 幻读3.4 更新丢失 4. 事务的隔离级别5. 事务的使用结语 前言 假设我们现在需要操作数据库进行转账,A 给 B 转账 100 块钱&…...

ubuntu链接mysql
C链接mysql 报错 sudo apt-get update sudo apt-get install libmysqlclient-dev 指令编译 g -o mysql_example mysql_example.cpp -I/usr/include/mysql -lmysqlclient g mysql_test.cpp mysql_config --cflags --libs 安装mysql sudo apt updatesudo apt install mysql-…...

QStyledItemDelegate 和 QItemDelegate 的作用
在Qt中,QStyledItemDelegate和QItemDelegate是用于自定义和控制项视图控件(如QListView、QTableView、QTreeView)中项的显示和编辑的委托类。它们提供了对项的外观和编辑行为的定制能力。尽管它们在功能上有相似之处,但它们之间有…...
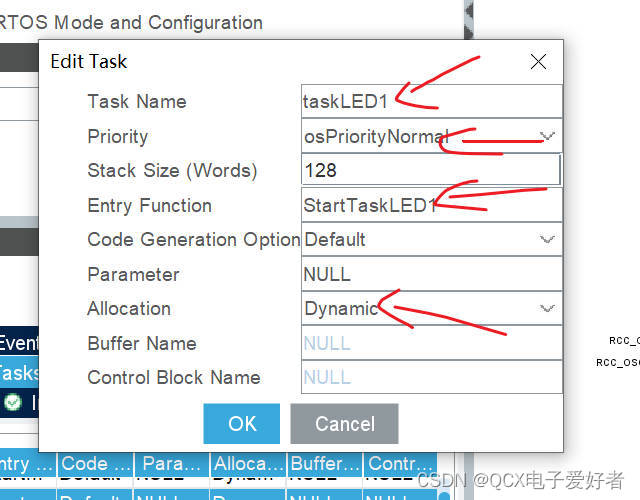
3.任务的创建与删除
1.什么是任务? 任务可以理解为进程/线程,创建一个任务,就会在内存开辟一个空间。 任务通常都含有while(1)死循环 2.任务创建与删除相关的函数 3.CUBEMAX相关配置 编辑一个led1闪烁的任务...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
