「计算机组成原理」数据的表示和运算(二)
文章目录
- 五、奇偶校验码
- 六、算术逻辑单元ALU
- 6.1 电路的基本原理
- 6.2 加法器的设计
- 6.2.1 一位全加器
- 6.2.2 串行加法器
- 6.2.3 串行进位的并行加法器
- 6.2.4 并行进位的并行加法器
- 七、补码加减运算器
- 八、标志位的生成
- 九、定点数的移位运算
- 9.1 算数移位
- 9.2 逻辑移位
- 9.3 循环移位
五、奇偶校验码
信息在传递的过程中可能会因为噪声的干扰而发生比特位的跳变,为了检查数据传输过程中是否发生了错误,我们会使用一系列的校验码来检查收到的信息。奇偶校验码就是一种简单的手段。假设要传输的信息7bit,我们在最高位添加上1bit的校验位。奇校验要求再添加过校验位之后,整个8bit信息中字符“1”的个数是奇数;偶校验则要求该数值为偶数。
对于偶校验,计算机想要得到校验位只需要将原本的所有信息位做异或即可。同样,若要检查收到的信息是否出错,只需要将接收到的8bit的信息做异或,结果为“1”则出错,但是结果为“0”并不代表没有错误,这是因为如果有偶数个bit发生跳变,异或的结果是不变的。因此奇偶校验码无法检测出偶数位错误。
六、算术逻辑单元ALU
ALU是运算器的核心部件,它的主要功能是做一些算术运算和逻辑运算。我们可以通过最基本的逻辑门电路,组合出自己需要的电路来实现不同的运算。

6.1 电路的基本原理
我们所说的比特0或1是通过给电子元器件加电压来实现的,低电压为0,高电压为1.最基本的三种基本的逻辑运算为逻辑与、逻辑或、逻辑非,将他们的门电路组合起来就可以得到我们想要的不同逻辑运算。其中逻辑异或与加法、偶校验有着天然的对应关系。
6.2 加法器的设计
6.2.1 一位全加器
假设A、B分别表示要相加的两个二进制数,Ai、BiA_{i}、B_{i}Ai、Bi表示A和B的第i位,SiS_{i}Si表示第i位和。如果我们简单的认为Si=Ai+BiS_{i}=A_{i}+B_{i}Si=Ai+Bi,这是有问题的,因为低位向本位的进位也是必须要考虑的一个因素,我们将它记为Ci−1C_{i-1}Ci−1,那么第i位和的正确表达是应该是Si=Ai+Bi+Ci−1S_{i}=A_{i}+B_{i}+C_{i-1}Si=Ai+Bi+Ci−1。我们来统计一下这个表达式的可能取值:
| AiA_{i}Ai | BiB_{i}Bi | Ci−1C_{i-1}Ci−1 | SiS_{i}Si | CiC_{i}Ci |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
可以看出,第i位和SiS_{i}Si只有在Ai、Bi和Ci−1A_{i}、B_{i}和C_{i-1}Ai、Bi和Ci−1三者中有奇数个“1” 时为“1”,否则为“0”.这个逻辑很“异或”。
第i为向高位产生的进位CiC_{i}Ci在两种情况下为“1”:1.Ai、BiA_{i}、B_{i}Ai、Bi都为“1”时。2.Ai、BiA_{i}、B_{i}Ai、Bi有一个为“1”并且Ci−1C_{i-1}Ci−1为“1”时。
于是便可以写出SiS_{i}Si和CiC_{i}Ci的逻辑表达式:
Si=Ai⊕Bi⊕Ci−1S_{i}=A_{i}\oplus B_{i}\oplus C_{i-1}Si=Ai⊕Bi⊕Ci−1
Ci=AiBi+(Ai⊕Bi)Ci−1C_{i}=A_{i}B_{i}+(A_{i}\oplus B_{i})C_{i-1}Ci=AiBi+(Ai⊕Bi)Ci−1
有了逻辑表达式也就有了电路,接下来只需要按照逻辑表达式将对应的门电路连接好就可以得到一位全加器。

6.2.2 串行加法器
串行加法器的实现方式是在一个全加器的基础上添加一个进位触发器,用来保存第i位产生的进位。将SiS_{i}Si作为该触发器的输入端,Ci−1C_{i-1}Ci−1作为该触发器的输出端,这就使得想要计算两个数的和必须要逐位计算。若计算nbit的数相加,就需要分n次计算,计算的结果也需要串行地、逐位地存入寄存器。

6.2.3 串行进位的并行加法器
串行进位的并行加法器就是将n个全加器串接起来,这样就可以直接进行两个nbit的数相加。这种加法器的缺点也比较明显:高位需要等待低位来的进位才能够计算,因此效率并不高。

6.2.4 并行进位的并行加法器
由于串行进位的并行加法器效率不高的主要原因是来自低位的进位需要等待低位的计算,因此想要提高计算速度,可以从该处入手。
根据之前计算过的逻辑表达式Ci=AiBi+(Ai⊕Bi)Ci−1C_{i}=A_{i}B_{i}+(A_{i}\oplus B_{i})C_{i-1}Ci=AiBi+(Ai⊕Bi)Ci−1不难看出,该表达式可以递归,只需要将Ci−1C_{i-1}Ci−1继续向下逐层展开代入,最终会展开到关于A、B的每一位和C0C_{0}C0表达式,而这些信息都是一开始就知道的,这也就意味着我们需要的进位信息可以直接得到,不需要等待低位的计算,这样就大大地提高了计算效率。

七、补码加减运算器
对于补码加法来说,前边设计的加法器完全可以满足需求。而对于补码的减法,在「计算机组成原理」数据的表示和运算(一)3.2.2中提到过,我们要先将减法转换成加法,方法就是全部位按位取反末位+1。
全部位按位取反我们只需要在加法器的其中一个加数的位置连接一个多路选择器,其功能是保证做减法时,先把操作数按位取反。
末位+1我们可以设置一个控制信号Sub,将其与多路选择器和低位的进位CinC_{in}Cin相连,其值为1时代表减法,值为0时代表加法。这样就实现了按位取反末位+1的操作。

由于无符号数的加减运算和补码的加减运算方式一样,因此此套电路也适用于无符号数的加减运算。
八、标志位的生成
除了之前的几个输出信息之外,标志位也是一个加法器重要的输出信息。主要的标识为有4个,分别是OF、SF、ZF和CF.其中OF和SF仅对有符号数的运算才有意义,CF仅对无符号数的运算才意义。

九、定点数的移位运算
定点数的移位运算可以快速的扩大或缩小定点数的倍数。对于有符号数,可以使用算数移位。对于无符号数,可以使用逻辑移位或循环移位。
9.1 算数移位
由于正数的三码一样,因此他们算数移位的方式也是一样的:右移舍弃低位,高位补0;左移舍弃高位,低位补0. 由于会有舍弃,因此若舍弃的位不为0,会出现误差甚至严重的错误(因为左移舍弃的是主要的高位)
对于负数来说就要分为原码、反码和补码三种情况分别讨论:
1.负数的原码:右移舍弃低位,高位补0;左移舍弃高位,低位补0.
2.负数的反码:右移舍弃低位,高位补1;左移舍弃高位,低位补1.
3.负数的补码:右移舍弃低位,高位补1;左移舍弃高位,低位补0.
原码和反码的补位方法很容易会想到。补码之所以高位补1低位补0是因为补码是在反码的基础上+1得到的,因此补码的最低位一定是与原码一致的,因此要左移遵循原码的方式。而右移相当于扩展的是反码的位置,因此需要遵循反码的方式补1.其实稍作分析就会发现,负数补码从低位向高位的第一个“1”及其右边的所有位和原码一样;该“1”左边的所有位同反码一样。
总结一下:
| 码制 | 填补代码 | |
|---|---|---|
| 正数 | 原码、补码、反码 | 0 |
| 负数 | 原码 | 0 |
| 反码 | 1 | |
| 补码 | 右移补1 | |
| 左移补0 |
9.2 逻辑移位
逻辑移位一般是对于无符号数来说的,他的规则比较简单,无论左右还是右移,舍弃相应的位然后在新位置补0即可。
9.3 循环移位
循环移位分为两种:带进位位CF的循环移位和不带进位位CF的循环移位。都很简单,顾名思义,就是把移出的部分补到空出的部分。带CF那CF就跟着一起移动;不带CF那CF就不要动,让剩下所有位进行循环移位。

相关文章:

「计算机组成原理」数据的表示和运算(二)
文章目录五、奇偶校验码六、算术逻辑单元ALU6.1 电路的基本原理6.2 加法器的设计6.2.1 一位全加器6.2.2 串行加法器6.2.3 串行进位的并行加法器6.2.4 并行进位的并行加法器七、补码加减运算器八、标志位的生成九、定点数的移位运算9.1 算数移位9.2 逻辑移位9.3 循环移位五、奇偶…...
建立自己的博客
环境安装: w10系统安装 第一步:安装git Git 官网: https://git-scm.com/ 第二步:安装Node.js Node.js官网:https://nodejs.org/zh-cn/ 使用cmd检测: node -v 第三步:安装Hexo Hexo官网:htt…...
Docker 安装mysql Mac 环境下
已安装桌面端 Docker (Mac安装Docker) 安装方式一 打开链接 https://www.docker.com/products/docker-desktop 选择平台下载 安装方式二 安装homebrew /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/m…...
《C++代码分析》第三回:类成员函数覆盖父类函数的调用(分析this指针的变化)
一、前言 在C的学习中我们知道,子类是可以覆盖父类的方法,这里我们探讨一下子类方法调用父类方法时this指针时如何变化的。 二、示例代码 #include "windows.h" #include "windef.h" #include <iostream> #include <tch…...

Altium designer--软件简介及安装教程(Altium designer16)
一、软件介绍(完整安装包资源见文末链接,含破解license) Altium Designer 是一款简单易用、原生3D设计增强的一体化设计环境,结合了原理图、ECAD库、规则和限制条件、BoM、供应链管理、ECO流程和世界一流的PCB设计工具。通过原理…...

Windows系统下基于开源软件的多物理场仿真
Windows系统下基于开源软件的多物理场仿真实践技术应用随着计算机技术的发展,计算机仿真技术日益成为继实验和理论之后的第三种重要研究和设计手段。真实世界中遇到的问题往往是固体力学,流体力学,热,电磁等多种现象耦合而成&…...

【STL】list剖析及模拟实现
✍作者:阿润菜菜 📖专栏:C 初识list 1. list基本概况 list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立…...

Go打包附件内容到执行文件
前言 如果我们的应用在启动的时候需要对数据库进行初始化(比如建表等), 可以通过读取.sql文件内容直接执行. 但是, 这样会带出一个问题: 在发送可执行文件的时候, 需要连带着附件文件, 并且相对路径还不能出错. 这样太麻烦了有时我们并不希望附件的内容被使用者看到 处于种种…...

Spring的配置属性
介绍 以前都是用XML来设置属性值,SpringBoot的自动配置可以简化Spring应用的开发。配置属性只是配置Spring应用上下文中bean的属性而已,可以通过多个源来配置,包括JVM系统属性、环境变量等。 Spring中有两种不同(但相关)的配置 bean装配&…...

132.《render-props, Hoc,自定义hooks 详解》
文章目录render-props 模式props 方式children 方式(推荐)Hoc(高阶组件)使用步骤示例props 丢失解决方案自定义 hook1.只执行一次2.防抖hook高阶组件与自定义hook有什么区别相同点不同点React 中代码逻辑复用有三种方式,render-props, Hoc&am…...

通过Session共享数据验证码进行用户登录
通过Session共享数据验证码进行用户登录 需求: 访问带有验证码的登录页面login.jsp。用户输入用户名,密码以及验证码。 ①。如果用户名和密码输入有误,跳转登陆页面,提示:用户名或密码错误。 ②。如果验证码输入有误…...
C++STL详解(六)——stack和queue
文章目录空间适配器stackstack的定义方式stack的使用stack的模拟实现queuequeue的定义方式queue的使用queue的模拟实现空间适配器 适配器是一种设计模式(设计模式是一套被反复使用的,多数人知晓的,经过分类编目的,代码设计经验的…...

javaEE 初阶 — CSS 的 基本语法 与 引入方式
文章目录1. 基本语法规范2. 三种引入方式1. 基本语法规范 CSS 的基本语法规范是由 选择器 和 若干个声明 组成的。 选择器选中一个元素之后,这些属性都是针对于这个元素展开的。 先来看一个没有 CSS 的效果。 <body><p>这是一个段落</p> </bo…...
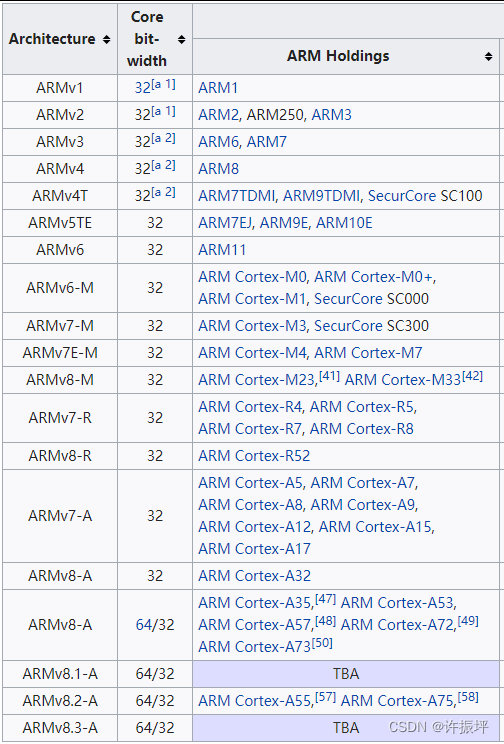
QEMU启动ARM32 Linux内核
目录前言前置知识ARM Versatile Express开发板简介ARM处理器家族简介安装qemu-system-arm安装交叉编译工具交叉编译ARM32 Linux内核交叉编译ARM32 Busybox使用busybox制作initramfs使用QEMU启动ARM32 Linux内核模拟vexpress-a9开发板模拟vexpress-a15开发板参考前言 本文介绍采…...

than的用法合集
首先需要了解一下than的词性,其有两个词性,一个是介词,一个是连词。 介词后面一定要接上名词性的词语,比如 i am taller then him 我比我的老师高 连词就比较自由,一般用来连接两个句子;但是使用than连词词…...
)
Unet 基于TCGA颅脑肿瘤MRI分割(高阶API分割模型)
目录 1. 介绍 2. dice 指标 3. resnet34 作为 backbone 的分割 4. deeplabv3 图像分割 4.1 问题 4.2 训练 4.3 预测 5. MAnet 图像分割...

[NIPS 2017] Improved Training of Wasserstein GANs (WGAN-GP)
Contents IntroductionDifficulties with weight constraintsCapacity underuseExploding and vanishing gradientsGradient penaltyReferencesIntroduction WGAN 增加了 GAN 模型训练的稳定性,但有时仍然会有生成质量不高或难以收敛的问题。作者发现上述问题经常是由 WGAN 中…...
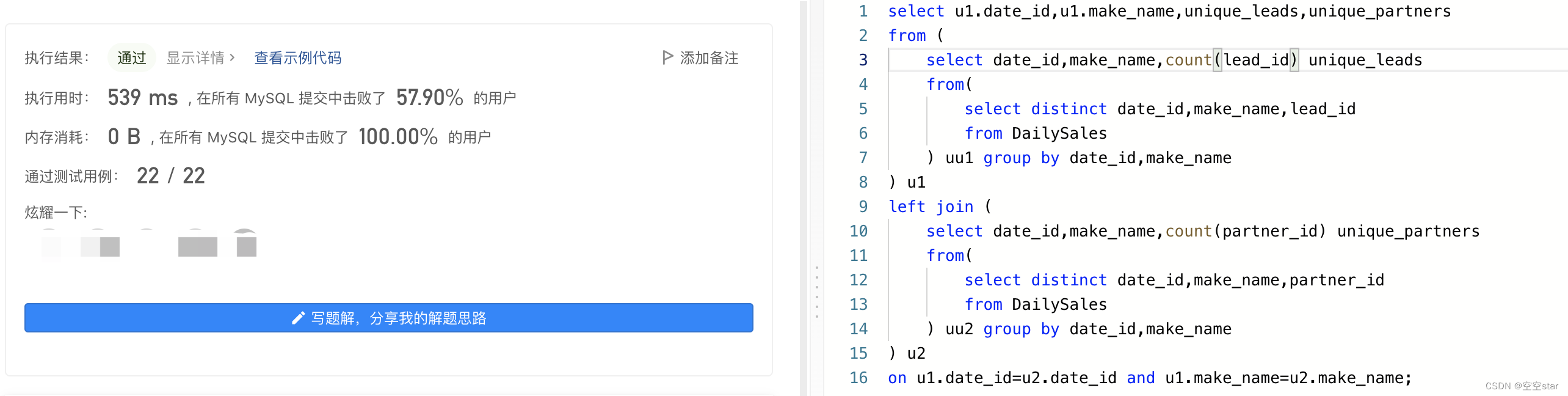
力扣-每天的领导和合伙人
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1693. 每天的领导和合伙人二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.…...

考虑分配与合并,用GO实现GCMarkSweep
完整源码 ≧ω≦ 希望各位爸爸们,给我点赞吧 kokool/GCByGo: 《垃圾回收的算法与实现》有感而发 (github.com) 书接上文 我们之前不考虑分配与合并情况下,用GO实现GCMarkSweep(标记清除算法),而这次我们继续回顾书本…...

浙江大学海宁IMBA提面经验分享
先来介绍一下我的个人情况:本人毕业于浙江一所普通的本科院校,毕业已经6年了,在一家互联网公司担任市场部经理。其实在参加浙大IMBA项目提面之前,我也参加了浙大MBA项目的提面,可惜只拿到了良好的结果,所以…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
