Leetcode 102.目标和
给定一个正整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
思路:
看到数字的范围,以及状态状态是可以从上一层转移的,所以考虑动态规划
当然也可以使用dfs(思路会更简单一些)
状态表示:
f[i][j]表示前i个数字,总和为k的方案数量
这里每个数字都是必须选的
状态转移:
由于每个数字都相当于是必须选的,所以说不存在不选i的情况,所以不能不选i直接从i-1层状态转移过来,不选i这一情况的状态转移不用考虑了
状态转移方程:
if(k-nums[i]+m>=0)f[i][k+m]+=f[i-1][k-nums[i]+m];if(k+nums[i]+m<=2*m)f[i][k+m]+=f[i-1][k+nums[i]+m];
注意初始化的时候应该+=1,因为为第一个数为0的时候直接赋值为1会丢失一种情况
代码:
class Solution {
public:int f[21][2100];int findTargetSumWays(vector<int>& nums, int target) {int n=nums.size();int m=0;for(int i=0;i<n;i++)m+=nums[i];if(m<abs(target))return 0;memset(f,0,sizeof f);//f[i][k]表示第i个数总和为k的方案数//cout<<f[0][m+nums[0]]<<endl;f[0][m+nums[0]]+=1;//cout<<f[0][m+nums[0]]<<endl;f[0][m-nums[0]]+=1;//这里必须是+=1因为nums[0]可能为0,这时候如果=1就少了一种情况//cout<<f[0][m+nums[0]]<<endl;for(int i=1;i<n;i++)for(int k=-m;k<=m;k++)//枚举总和{//f[i][k+m]=max(f[i-1][k+m],f[i][k+m]); 由于第i个数不能不选,所以说不能不选i,进而从i-1这个状态直接转移过来if(k-nums[i]+m>=0)f[i][k+m]+=f[i-1][k-nums[i]+m];if(k+nums[i]+m<=2*m)f[i][k+m]+=f[i-1][k+nums[i]+m];}return f[n-1][m+target];}
};
运行结果:
相关文章:

Leetcode 102.目标和
给定一个正整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添加 ‘-’ &…...

LLM AI工具和Delphi名称的起源
LLM AI工具和Delphi名称的起源 使用ChatGPT,直接或通过微软工具,以及其他基于llm的引擎。我很欣赏他们提供好的总结和比较的能力,并且还编写了一些样板代码。与此同时,当你问一些重要的问题时,你会得到一些令人惊讶的好…...
打破数据分析壁垒:SPSS复习必备(十一)
一、方差分析 方差分析的应用条件如下: (1)独立,各组数据相互独立,互不相关; (2)正态:即各组数据符合正态分布; (3)方差齐性&…...

【十六】【QT开发应用】Menu菜单,contextMenuEvent,setContextMenuPolicy,addAction
在 Qt 框架中,QMenu 类用于创建和管理菜单。菜单是用户界面的一部分,可以包含多个选项或动作,用户可以选择这些选项来执行特定的功能。菜单通常显示在菜单栏、上下文菜单(右键菜单)或工具栏中。 基本用法 创建菜单对象…...

华为DCN技术:M-LAG
M-LAG(Multichassis Link Aggregation Group)即跨设备链路聚合组,是一种实现跨设备链路聚合的机制。M-LAG主要应用于普通以太网络、VXLAN和IP网络的双归接入,可以起到负载分担或备份保护的作用。相较于另一种常见的可靠性接入技术…...

k8s持久化之emptyDir使用
目录 概述实践代码 概述 理解emptyDir使用,是后续k8s持久化进阶,高阶使用的基础。 实践 代码 详细说明在代码中 # 缓存数据,可以让多个容器共享数据 # 删除 Pod 时,emptyDir 数据同步消失 # 定义 initContainer -> 下载数据…...
Java露营基地预约小程序预约下单系统源码
轻松开启户外探险之旅 🌟 露营热潮来袭,你准备好了吗? 随着人们对户外生活的热爱日益增加,露营已成为许多人周末和假期的首选活动。但你是否曾因找不到合适的露营基地而烦恼?或是因为繁琐的预约流程而错失心仪的营地…...
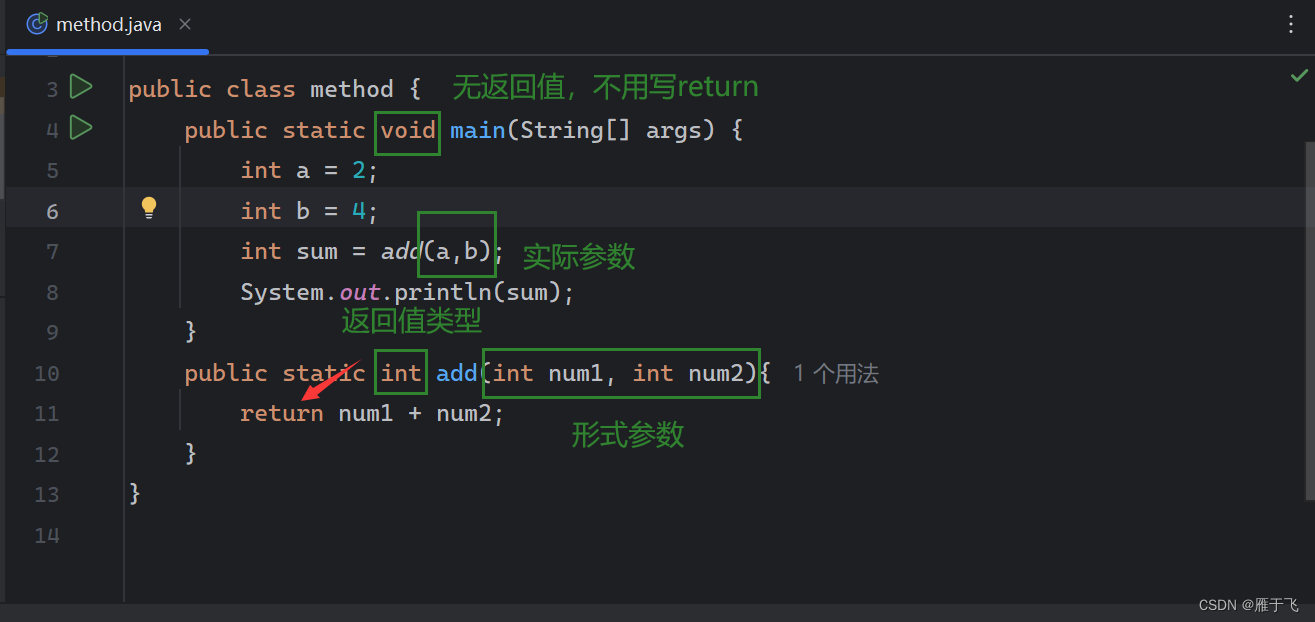
七天速通javaSE:第四天 java方法
文章目录 前言一、什么是方法?二、方法的定义与调用1. 方法的定义2. 方法的调用3. 练习:定义比大小方法并调用 三、方法的重载四、递归五、可变参数拓展:命令行传递参数 前言 本章将学习java方法。 一、什么是方法? java方法是用…...

jupyter notebook的markdown语法不起作用
在这个界面编辑,发现markdown你编辑的是什么就是什么,不起作用,然而点一下: 右上角“Notebook转发”,就会单独跳出一个jupyter notebook的界面,此时就会奏效:...
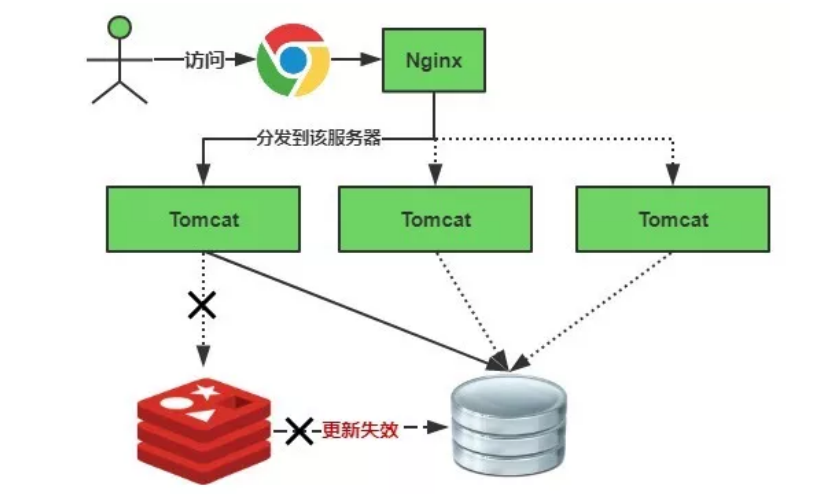
Redis 学习笔记(2)
目录 1 Redis的持久化1.1 RDB持久化方案1.2 AOF持久化方案 2 Redis架构2.1 主从复制架构2.2 哨兵集群设计2.3 哨兵集群设计 3 Redis事务机制4 Redis过期策略与内存淘汰机制4.1 过期策略4.2 内存淘汰机制 5 Redis高频面试题4.1 缓存穿透4.2 缓存击穿4.3 缓存雪崩 1 Redis的持久化…...

快慢指针:删除有序数组中的重复项
题目链接:. - 力扣(LeetCode) 思路好想,代码实现不好想 class Solution {public int removeDuplicates(int[] nums) {int fast 1,slow 1;while(fast < nums.length){if(nums[fast] ! nums[fast-1]){nums[slow] nums[fast]…...

用户登录错误次数太多锁定账号
当用户登录验证码错误次数太多时,需要限制用户在10分钟之内不能再次登录。 限制方案: 1.通过Redis ZSet key可以设置为用户名,value可以设置为UUID,score设置为当前时间戳 每次用户登录时,通过 rangeByScore 查询对…...

tedsign vue3 web-端框架中封装一个验证码组件 以及对应node 接口逻辑说明
一个这样的组件 我直接上代码了 <template><t-loading size"small" :loading"loading" show-overlay><div class"container" click"refresh"><div v-if"svg" class"svg" v-html"svg&…...

探索Scala并发编程之巅:高效并行处理的艺术
标题:探索Scala并发编程之巅:高效并行处理的艺术 引言 在现代软件开发中,随着多核处理器的普及,编写能够充分利用硬件能力的并发程序变得至关重要。Scala,这门结合了面向对象和函数式编程特性的语言,提供…...

AudioLM: 音频生成的革命性模型
AudioLM: 音频生成的革命性模型 AudioLM是一种革命性的音频生成模型,它结合了深度学习和自然语言处理的先进技术,能够生成高质量、逼真的音频内容。本文将探讨AudioLM的基本原理、工作机制、应用场景以及对音频生成领域的影响和未来发展方向。 一、Aud…...

C++ Vector的模拟实现
vector的介绍 1. vector是表示可变大小数组的序列容器。 2. 就像数组一样,vector也采用的连续存储空间来存储元素。也就是意味着可以采用下标对vector的元素进行访问,和数组一样高效。但是又不像数组,它的大小是可以动态改变的,而…...

Kubernetes之Controller详解
本文尝试从Kubernetes Controller的种类、交互逻辑、最佳实践、伪代码示例及历史演进5个方面对其进行详细阐述,希望对您有所帮助! 一、Kubernetes Controller种类 Kubernetes Controller Manager 是 Kubernetes 集群的核心组件之一,负责管理…...

openlayers性能优化——开启图层预加载、减少空白等待时间
使用切片图层时、地图拖拽会有空白图片,为了减少空白等待时间,我们可以开始图层预加载。 const map_top new Map({layers: [new TileLayer({preload:Infinity, //预加载source: new StadiaMaps({layer: "outdoors",}),}),],target: "ma…...
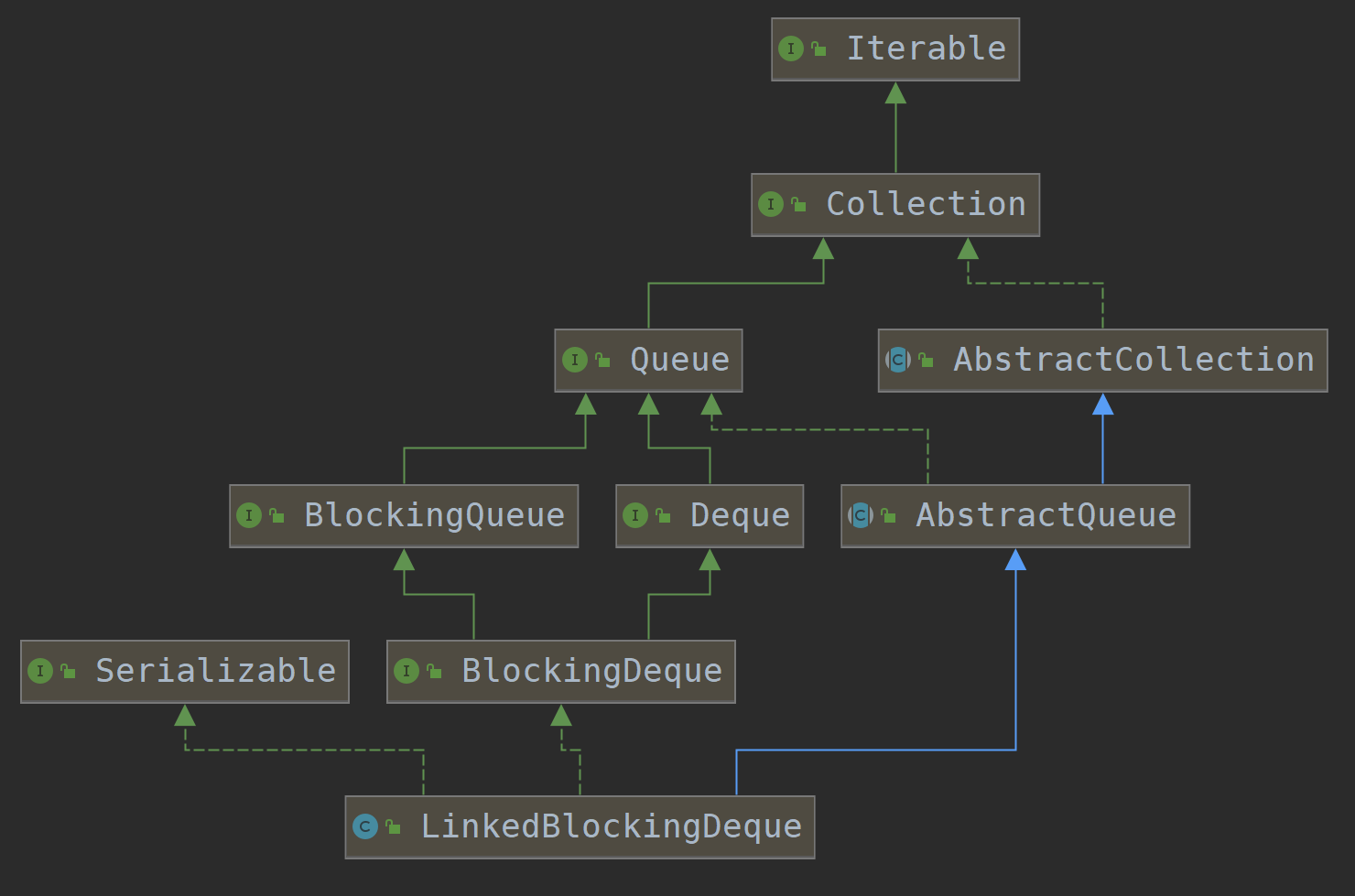
BlockingQueue详解(含动画演示)
目录 BlockingQueue详解0、BlockingQueue简介BlockingQueue接口中方法注释BlockingQueue的实现,总结计划 1、ArrayBlockingQueue简介2、ArrayBlockingQueue的继承体系3、ArrayBlockingQueue的构造方法①、 ArrayBlockingQueue(int capacity)②、ArrayBlockingQueue(…...

wordpress商用付费主题与免费主题的区别
WordPress免费主题与WordPress付费主题,都可以用,但存在非常大的差别。从直观的感受,简单地说就是,WordPress免费主题能用,WordPress付费主题好用。如果涉及到其它的方面,WordPress商用付费主题与免费主题之…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
