7.3 向量的数量积与向量积
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人!
🌙个人主页:阿芒的主页
⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学这门课的知识点,参考书主要为经典的同济版第七版《高等数学》以及作者在高校使用的《高等数学》系统教材。梳理《高等数学》这门课,旨在帮助那些刚刚接触这门课的小白以及需要系统复习这门课的考研人士。希望自己的一些经验能够帮助更多的人。
文章目录
- 向量的数量积
- 向量的向量积
向量的数量积
- 定义:
设向量a→\overrightarrow{a}a,b→\overrightarrow{b}b的夹角为θ\thetaθ,称
∣a→∣∣b→∣cos|\overrightarrow{a}||\overrightarrow{b}|cos∣a∣∣b∣cos θ\thetaθ记作a→⋅b→\overrightarrow{a}\cdot\overrightarrow{b}a⋅b为a→\overrightarrow{a}a与b→\overrightarrow{b}b的数量积(点积、内积)
- 性质
(1)a→⋅a→\overrightarrow{a}\cdot\overrightarrow{a}a⋅a=∣a→∣2|\overrightarrow{a}|^{2}∣a∣2
(2)a→\overrightarrow{a}a,b→\overrightarrow{b}b为两个非零向量,则有a→⋅b→\overrightarrow{a}\cdot\overrightarrow{b}a⋅b=0⟺\Longleftrightarrow⟺a→⊥b→\overrightarrow{a}\bot\overrightarrow{b}a⊥b
注:由于零向量的方向是任意的,所有规定零向量与任何向量都垂直.
- 运算规律
(1)交换律:a→⋅b→\overrightarrow{a}\cdot\overrightarrow{b}a⋅b=b→⋅a→\overrightarrow{b}\cdot\overrightarrow{a}b⋅a
(2)结合律:(λa→)⋅b→(\lambda\overrightarrow{a})\cdot\overrightarrow{b}(λa)⋅b=a→⋅(λb→)\overrightarrow{a}\cdot(\lambda\overrightarrow{b})a⋅(λb)=λ(a→⋅b→)\lambda(\overrightarrow{a}\cdot\overrightarrow{b})λ(a⋅b)
~~~~~~~~~~~~~~~~~ (λa→)⋅(μb→)(\lambda\overrightarrow{a})\cdot(\mu\overrightarrow{b})(λa)⋅(μb)=λ(a→⋅(λb→))\lambda(\overrightarrow{a}\cdot(\lambda\overrightarrow{b}))λ(a⋅(λb))=λμ(a→⋅b→)\lambda\mu(\overrightarrow{a}\cdot\overrightarrow{b})λμ(a⋅b)(其中λ,μ\lambda,\muλ,μ为实数)
(3)分配律:(a→+b→)⋅c→(\overrightarrow{a}+\overrightarrow{b})\cdot\overrightarrow{c}(a+b)⋅c=a→⋅c→\overrightarrow{a}\cdot\overrightarrow{c}a⋅c+b→⋅c→\overrightarrow{b}\cdot\overrightarrow{c}b⋅c
- 坐标表示
-
设a→\overrightarrow{a}a=axi→+ayj→+azk→a_{x}\overrightarrow{i}+a_{y}\overrightarrow{j}+a_{z}\overrightarrow{k}axi+ayj+azk,b→\overrightarrow{b}b=bxi→+byj→+bzk→b_{x}\overrightarrow{i}+b_{y}\overrightarrow{j}+b_{z}\overrightarrow{k}bxi+byj+bzk,则
a→⋅b→\overrightarrow{a}\cdot\overrightarrow{b}a⋅b=axbx+ayby+azbza_{x}b_{x}+a_{y}b_{y}+a_{z} b_{z}axbx+ayby+azbz -
两向量夹角公式
当 a→\overrightarrow{a}a,b→\overrightarrow{b}b为两个非零向量时,由于a→⋅b→\overrightarrow{a}\cdot\overrightarrow{b}a⋅b=∣a→∣∣b→∣cos|\overrightarrow{a}||\overrightarrow{b}|cos∣a∣∣b∣cos θ\thetaθ,从而
cosθcos\thetacosθ= a→⋅b→∣a→∣∣b→∣\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}∣a∣∣b∣a⋅b=axbx+ayby+azbzax2+ay2+az2bx2+by2+bz2\frac{a_{x}b_{x}+a_{y}b_{y}+a_{z} b_{z}}{ \sqrt{a^{2}_{x}+a^{2}_{y}+a^{2}_{z} }\sqrt{b^{2}_{x}+b^{2}_{y}+b^{2}_{z} }}ax2+ay2+az2bx2+by2+bz2axbx+ayby+azbz -
两向量垂直的充要条件
a→⊥b→\overrightarrow{a}\bot\overrightarrow{b}a⊥b⟺\Longleftrightarrow⟺axbx+ayby+azbz=0a_{x}b_{x}+a_{y}b_{y}+a_{z} b_{z}=0axbx+ayby+azbz=0
向量的向量积
- 定义
设向量a→\overrightarrow{a}a,b→\overrightarrow{b}b的夹角为θ\thetaθ,定义
向量c→\overrightarrow{c}c:①方向:c→⊥a→\overrightarrow{c}\bot\overrightarrow{a}c⊥a,c→⊥b→\overrightarrow{c}\bot\overrightarrow{b}c⊥b且符合右手规则
~~~~~~~~~~~~~ ②模:∣c→∣|\overrightarrow{c}|∣c∣=∣a→∣∣b→∣sin|\overrightarrow{a}||\overrightarrow{b}|sin∣a∣∣b∣sin θ\thetaθ
称c→\overrightarrow{c}c为a→与b→\overrightarrow{a}与\overrightarrow{b}a与b为的向量积(叉积),记作c→\overrightarrow{c}c=a→×b→\overrightarrow{a}×\overrightarrow{b}a×b
- 性质
(1)a→×a→\overrightarrow{a}×\overrightarrow{a}a×a=0→\overrightarrow{0}0
(2)a→\overrightarrow{a}a,b→\overrightarrow{b}b为两个非零向量,则有a→×b→\overrightarrow{a}×\overrightarrow{b}a×b=0⟺\Longleftrightarrow⟺a→∥b→\overrightarrow{a}\parallel\overrightarrow{b}a∥b
- 运算规律
(1)a→×b→\overrightarrow{a}×\overrightarrow{b}a×b=-b→×a→\overrightarrow{b}×\overrightarrow{a}b×a
(2)结合律:(λa→)×b→(\lambda\overrightarrow{a})×\overrightarrow{b}(λa)×b=a→×(λb→)\overrightarrow{a}×(\lambda\overrightarrow{b})a×(λb)=λ(a→×b→)\lambda(\overrightarrow{a}×\overrightarrow{b})λ(a×b)
(3)分配律:(a→+b→)×c→(\overrightarrow{a}+\overrightarrow{b})×\overrightarrow{c}(a+b)×c=a→×c→\overrightarrow{a}×\overrightarrow{c}a×c+b→×c→\overrightarrow{b}×\overrightarrow{c}b×c
- 坐标表示
- 设a→\overrightarrow{a}a=axi→+ayj→+azk→a_{x}\overrightarrow{i}+a_{y}\overrightarrow{j}+a_{z}\overrightarrow{k}axi+ayj+azk,b→\overrightarrow{b}b=bxi→+byj→+bzk→b_{x}\overrightarrow{i}+b_{y}\overrightarrow{j}+b_{z}\overrightarrow{k}bxi+byj+bzk,则
a→×b→\overrightarrow{a}×\overrightarrow{b}a×b=(aybz−azby)i→+(azbx−axbz)j→+(axby−aybx)k→(a_{y}b_{z}-a_{z}b_{y})\overrightarrow{i}+(a_{z}b_{x}-a_{x} b_{z})\overrightarrow{j}+(a_{x}b_{y}-a_{y} b_{x})\overrightarrow{k}(aybz−azby)i+(azbx−axbz)j+(axby−aybx)k - 两个向量积的行列式表示
a→×b→\overrightarrow{a}×\overrightarrow{b}a×b=(aybz−azby)i→+(azbx−axbz)j→+(axby−aybx)k→(a_{y}b_{z}-a_{z}b_{y})\overrightarrow{i}+(a_{z}b_{x}-a_{x} b_{z})\overrightarrow{j} +(a_{x}b_{y}-a_{y} b_{x})\overrightarrow{k}(aybz−azby)i+(azbx−axbz)j+(axby−aybx)k = ∣i→j→k→axayazbxbybz∣\left| \begin{array}{cccc} \overrightarrow{i}&\overrightarrow{j}&\overrightarrow{k}\\ a_{x}&a_{y}&a_{z}\\ b_{x}&b_{y}&b_{z}\\ \end{array} \right| iaxbxjaybykazbz
相关文章:

7.3 向量的数量积与向量积
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人! 🌙个人主页:阿芒的主页 ⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学…...

Qt静态扫描(命令行操作)
Qt静态扫描(命令行操作) 前沿: 静态代码分析是指无需运行被测代码,通过词法分析、语法分析、控制流、数据流分析等技术对程序代码进行扫描,找出代码隐藏的错误和缺陷,如参数不匹配,有歧义的嵌…...

【Hadoop】配置文件
Hadoop 配置文件分两类:默认配置文件和自定义配置文件,只有用户想修改某一默认 配置值时,才需要修改自定义配置文件,更改相应属性值 (1)默认配置文件: cd $HADOOP_HOME/share/hadoop common路…...

python进程池
Python进程池是Python标准库中multiprocessing模块提供的一种用于管理进程的方式。它可以使Python程序以并行的方式执行任务,提高程序的运行效率。本篇博客将介绍如何使用Python进程池。 创建进程池 在使用Python进程池之前,我们需要先创建一个进程池对…...
笔记本固态盘数据丢失怎么办?笔记本固态盘怎么恢复数据
如果笔记本固态盘数据丢失怎么办?笔记本固态盘怎么恢复数据?下面将为大家详细地介绍一下笔记本固态硬盘数据恢复的三种实用方法,希望对大家有所帮助。一、简单恢复方法笔记本固态硬盘数据删除以后,较为简单直接的恢复方法就是从回…...
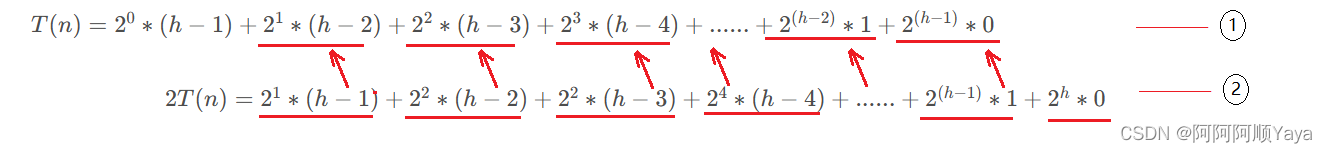
堆的结构与实现
堆的结构与实现二叉树的顺序结构堆的概念及结构堆的实现堆的创建向上调整建堆向下调整建堆堆的操作链接二叉树的顺序结构 堆其实是具有一定规则限制的完全二叉树。 普通的二叉树是不太适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树会更适合使用顺…...

Pandas快速入门
Pandas是Python中非常流行的数据处理库之一,它提供了一种简单而强大的方法来处理和分析数据。在本篇文章中,我将向你介绍Pandas的基础知识,以便你可以开始使用它来处理和分析数据。 安装Pandas 首先,你需要安装Pandas。可以通过…...
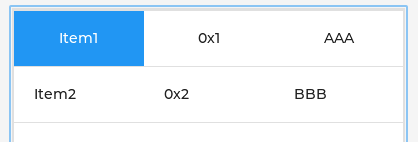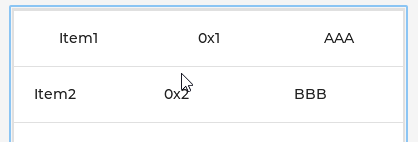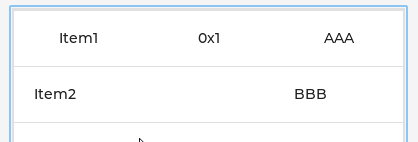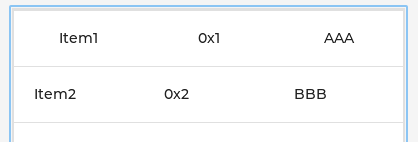
LVGL学习笔记18 - 表Table
目录 1. Parts 1.1 LV_PART_MAIN 1.2 LV_PART_ITEMS 2. 样式 2.1 设置行列数 2.2 设置单元格字符串 2.3 设置单元格宽度 2.4 设置表格高度和宽度 2.5 设置字符串颜色 2.6 设置边框颜色 2.7 设置背景颜色 3. 事件 4. CELL CTRL 表格是由包含文本的行、列和单元格构…...

嵌入式安防监控项目——html框架分析和环境信息刷新到网页
目录 一、html控制LED 二、模拟数据上传到html 一、html控制LED 简单来说就是html给boa服务器发了一个控制指令信息,然后boa转发给cgi进程,cgi通过消息队列和主进程通信。主进程再去启动LED子线程。 这是老师给的工程。 以前学32都有这工具那工具来管…...
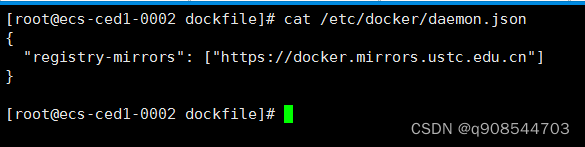
centos安装docker详细步骤
目录 一.前言 1.环境要求2.官网中文安装参考手册 二.安装步骤 1.卸载旧版本2.安装需要的软件包3.设置docker镜像源 1.配置docker镜像源 方式1:官网地址(外国):方式2:阿里云源:2.查看配置是否成功 4.更新yum软件包索引5.可以查看…...
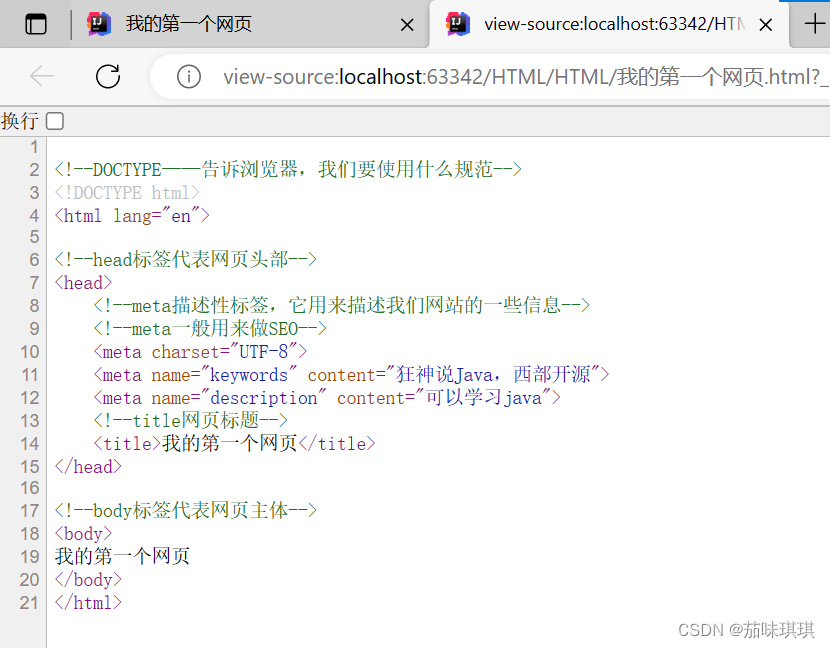
初识HTML、W3C标准、如何利用IDEA创建HTML项目、HTML基本结构、网页基本信息
一、什么是HTML? HTML——Hyper Text Markup Languagr(超文本标记语言) 超文本包括:文字、图片、音频、视频、动画等 目前网页中常用——HTML5 HTML5提供了一些新的元素和一些有趣的新特性,同时也建立了一些新的规则…...

为什么程序员喜欢这些键盘?
文章目录程序员的爱介绍个人体验程序员的爱 程序员是长时间使用计算机的群体,他们需要一款高品质的键盘来保证舒适的打字体验和提高工作效率。在键盘市场上,有很多不同类型的键盘,但是对于程序员来说,机械键盘是他们最钟爱的选择…...

JS中数组去重的几种方法
JS 中有多种方法可以实现数组去重,下面是几种常用的方法:1、使用 Set 去重:Set 数据结构中不能有重复元素,可以将数组转成 Set 类型,再转回数组。let arr [1,2,3,4,5,6,2,3,4]; let uniqueArr [...new Set(arr)]; co…...

Nginx 配置实例-负载均衡
一、实现效果 浏览器地址栏输入地址 http://192.168.137.129/edu/a.html,负载均衡效果,将请求平均分配到8080和8081两台服务器上。 二、准备工作 1. 准备两台tomcat服务器,一台8080,一台8081 (具体操作如下两个链接) Nginx配置实…...

引出生命周期、生命周期_挂载流程、生命周期_更新流程、生命周期_销毁流程、生命周期_总结——Vue
目录 一、引出生命周期 二、生命周期_挂载流程 三、生命周期_更新流程 四、生命周期_销毁流程 五、生命周期_总结 一、引出生命周期 生命周期: 1.又名:生命周期回调函数、生命周期函数、生命周期钩子。 2.是什么:Vue在关键时刻帮我们调…...

C++ STL学习之【vector的使用】
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 The power of imagination makes us infinite. 想象力的力量使我们无限。 文章目录📘前言📘正文1、默认成员函数1.1、默认构造…...

方差分析与单因素方差分析
研究分类型自变量对数值型因变量的影响。检验统计的设定和检验方法与变量间的方差是否相等有关。 例如研究行业、服务等级对投诉数的影响:如表格中给出4个行业、每个行业有3个服务等级、样本容量为7、观测值为投诉数。则构成一个3维的矩阵。 在上述基础上…...

分布式链路追踪组件skywalking介绍
SkyWalking组件概念 一个开源的可观测平台, 用于从服务和云原生基础设施收集, 分析, 聚合及可视化数据。SkyWalking 提供了一种简便的方式来清晰地观测分布式系统, 甚至横跨多个云平台。SkyWalking 更是一个现代化的应用程序性能监控(Application Performance Monitoring)系统…...
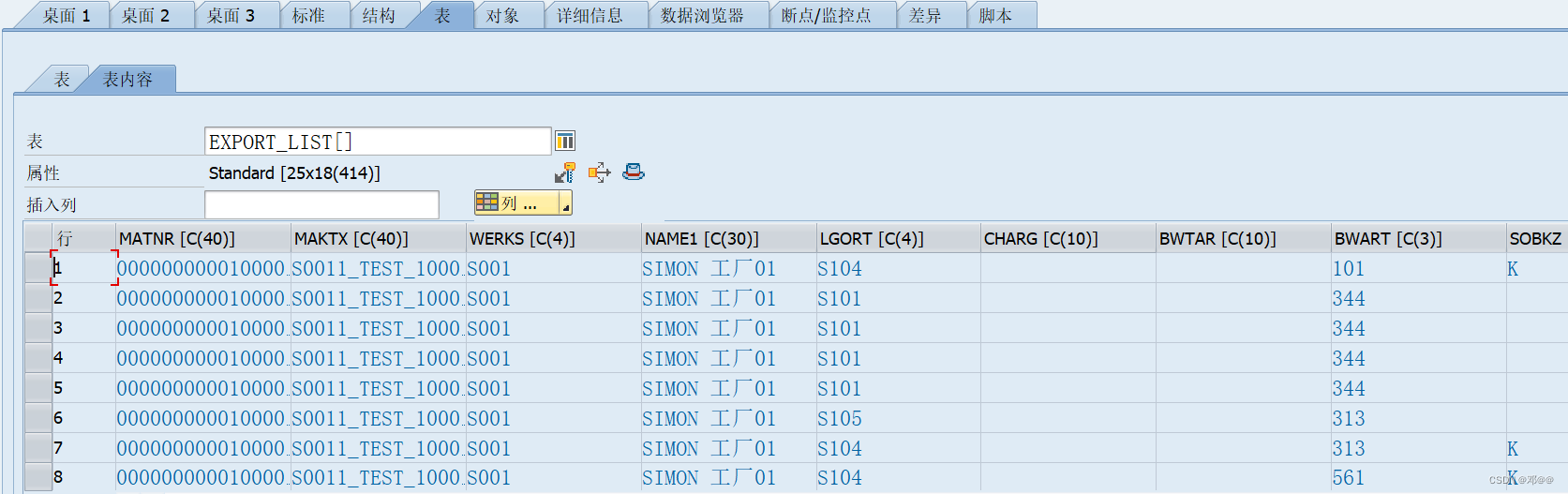
SUBMIT的用法
SUBMIT的用法 一、简介 系统MB52/MB51/MB5B等类似的报表 ,虽然数据很全面,执行效率也够快,但是经常会不满足用户需求(增添字段、添加查询条件等),很多ABAP 会选择去COPY出标准程序,然后去做修改…...

网页基本标签、图像标签、链接标签、块内元素和块元素、列表标签、表格标签
一、网页基本标签 标题标签 段落标签 未写段落标签前,文本没有按照想要的格式排列显示 写段落标签后: 每句都是一段,所以句与句距离比较宽 换行标签 同一段,只是把文字换行,所以比较紧凑 水平线标签 字体样式标签 …...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
