图的拓扑排序
图的拓扑排序(Topological Sorting)是一种线性排序,用于有向无环图(Directed Acyclic Graph,DAG)。拓扑排序将图中的顶点排成一个线性序列,使得对于每一条有向边 (u, v),顶点 u 都排在顶点 v 之前。常见的拓扑排序算法有 Kahn 算法和基于深度优先搜索(DFS)的算法。
1. Kahn 算法
Kahn 算法是一种基于入度的贪心算法,逐步选择入度为 0 的顶点并移除其出边。
步骤:
- 计算每个顶点的入度。
- 初始化一个队列,将所有入度为 0 的顶点入队。
- 重复以下步骤,直到队列为空:
- 从队列中取出一个顶点,将其添加到拓扑排序结果中。
- 对该顶点的每条出边,将目标顶点的入度减 1。如果目标顶点的入度变为 0,则将其入队。
- 如果结果中的顶点数与图中的顶点数相等,则拓扑排序成功,否则图中存在环。
Java实现:
import java.util.*;public class KahnTopologicalSort {static class Graph {int V;List<Integer>[] adjacencyList;Graph(int V) {this.V = V;adjacencyList = new LinkedList[V];for (int i = 0; i < V; i++) {adjacencyList[i] = new LinkedList<>();}}void addEdge(int src, int dest) {adjacencyList[src].add(dest);}List<Integer> topologicalSort() {int[] inDegree = new int[V];for (int i = 0; i < V; i++) {for (int neighbor : adjacencyList[i]) {inDegree[neighbor]++;}}Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < V; i++) {if (inDegree[i] == 0) {queue.add(i);}}List<Integer> topoOrder = new ArrayList<>();while (!queue.isEmpty()) {int u = queue.poll();topoOrder.add(u);for (int neighbor : adjacencyList[u]) {inDegree[neighbor]--;if (inDegree[neighbor] == 0) {queue.add(neighbor);}}}if (topoOrder.size() != V) {throw new RuntimeException("The graph has at least one cycle");}return topoOrder;}}public static void main(String[] args) {Graph graph = new Graph(6);graph.addEdge(5, 2);graph.addEdge(5, 0);graph.addEdge(4, 0);graph.addEdge(4, 1);graph.addEdge(2, 3);graph.addEdge(3, 1);List<Integer> topoOrder = graph.topologicalSort();System.out.println("Topological Sort: " + topoOrder);}
}
2. 基于深度优先搜索的拓扑排序
DFS 算法通过递归访问顶点,确保每个顶点在所有邻居顶点之后加入结果列表。
步骤:
- 初始化一个布尔数组,标记每个顶点是否被访问。
- 初始化一个栈,用于存储拓扑排序结果。
- 对每个顶点执行以下步骤(如果尚未被访问):
- 从该顶点开始进行 DFS。
- 在 DFS 过程中,将当前顶点标记为已访问,并递归访问所有未被访问的邻居顶点。
- DFS 完成后,将当前顶点压入栈。
- 从栈顶依次弹出顶点,形成拓扑排序结果。
Java实现:
import java.util.*;public class DFSTopologicalSort {static class Graph {int V;List<Integer>[] adjacencyList;Graph(int V) {this.V = V;adjacencyList = new LinkedList[V];for (int i = 0; i < V; i++) {adjacencyList[i] = new LinkedList<>();}}void addEdge(int src, int dest) {adjacencyList[src].add(dest);}void topologicalSortUtil(int v, boolean[] visited, Stack<Integer> stack) {visited[v] = true;for (int neighbor : adjacencyList[v]) {if (!visited[neighbor]) {topologicalSortUtil(neighbor, visited, stack);}}stack.push(v);}List<Integer> topologicalSort() {Stack<Integer> stack = new Stack<>();boolean[] visited = new boolean[V];for (int i = 0; i < V; i++) {if (!visited[i]) {topologicalSortUtil(i, visited, stack);}}List<Integer> topoOrder = new ArrayList<>();while (!stack.isEmpty()) {topoOrder.add(stack.pop());}return topoOrder;}}public static void main(String[] args) {Graph graph = new Graph(6);graph.addEdge(5, 2);graph.addEdge(5, 0);graph.addEdge(4, 0);graph.addEdge(4, 1);graph.addEdge(2, 3);graph.addEdge(3, 1);List<Integer> topoOrder = graph.topologicalSort();System.out.println("Topological Sort: " + topoOrder);}
}
结论
- Kahn算法:通过计算入度并逐步移除入度为 0 的顶点来实现拓扑排序。适用于在线性时间内完成排序,但需要额外的空间来存储入度。
- DFS算法:通过递归访问顶点来实现拓扑排序。适用于递归解决问题的场景,但需要维护递归栈和结果栈。
相关文章:

图的拓扑排序
图的拓扑排序(Topological Sorting)是一种线性排序,用于有向无环图(Directed Acyclic Graph,DAG)。拓扑排序将图中的顶点排成一个线性序列,使得对于每一条有向边 (u, v),顶点 u 都排…...

windows USB 设备驱动开发-总章
通用串行总线 (USB) 提供可扩展的即插即用串行接口,确保外围设备的标准、低成本的连接。 USB 设备包括键盘、鼠标、游戏杆、打印机、扫描仪、存储设备、调制解调器、视频会议摄像头等。USB-IF 是一个特别兴趣组 (SIG),负责维护官方 USB 规范、测试规范和…...
springboot解析自定义yml文件
背景 公司产品微服务架构下有十几个模块,几乎大部分模块都要连接redis。每次在客户那里部署应用,都要改十几遍配置,太痛苦了。当然可以用nacos配置中心的功能,配置公共参数。不过我是喜欢在应用级别上解决问题,因为并不…...

【C/C++】静态函数调用类中成员函数方法 -- 最快捷之一
背景 注册回调函数中,回调函数是一个静态函数。需要调用类对象中的一个成员函数进行后续通知逻辑。 方案 定义全局指针,用于指向类对象this指针 static void *s_this_obj;类构造函数中,将全局指针指向所需类的this指针 s_this_obj this…...

佣金的定义和类型
1. 佣金的定义 基本定义:佣金是指在商业交易中,代理人或中介机构为促成交易所获得的报酬。它通常是按交易金额的一定比例计算和支付的。支付方式:佣金可以是固定金额,也可以是交易金额的百分比。 2. 佣金的类型 销售佣金&#…...
)
python数据分析实训任务二(‘风力风向’)
import numpy as np import matplotlib.pyplot as plt # 数据 labelsnp.array([东风, 东北风, 北风, 西北风, 西风, 西南风, 南风, 东南风]) statsnp.array([2.1, 2, 0, 3, 1.5, 3, 6, 4]) # 将角度转换为弧度 anglesnp.linspace(0, 2*np.pi, len(labels), endpointFalse).toli…...
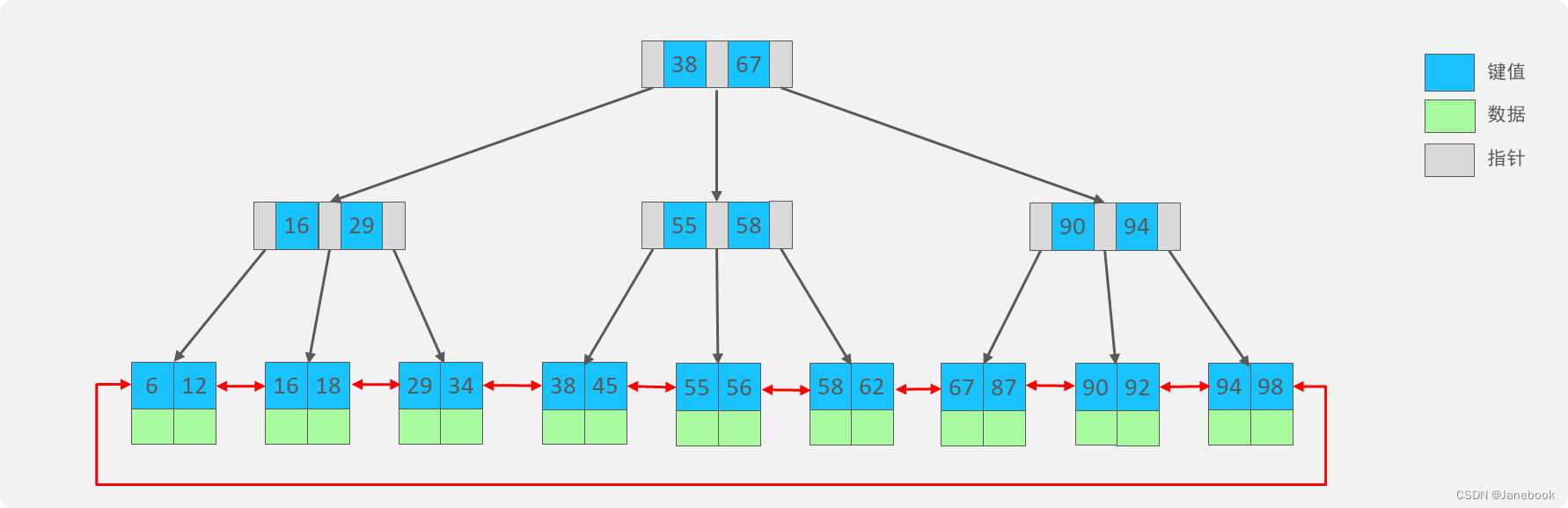
Java技术栈总结:数据库MySQL篇
一、慢查询 1、常见情形 聚合查询 多表查询 表数据量过大查询 深度分页查询 2、定位慢查询 方案一、开源工具 调试工具:Arthas运维工具:Prometheus、Skywalking 方案二、MySQL自带慢日志 在MySQL配置文件 /etc/my.conf 中配置: # …...

vue-cli 项目打包优化-基础篇
1、项目打包完运行空白 引用资源路径问题,打包完的【index.html】文件引用其他文件的引用地址不对 参考配置:https://cli.vuejs.org/zh/config 修改vue.config.js ,根据与 后端 或 运维 沟通修改 module.export {// 默认 publicPath: //…...

24/06/26(1.1129)动态内存
strtok 字符串分割函数 #include<stdio.h> int main(){ char str[] "this,a sample string."; char* sep ","; char* pch strtok(str, sep); printf("%s\n", pch); while (pch ! NULL){ printf("%s\…...
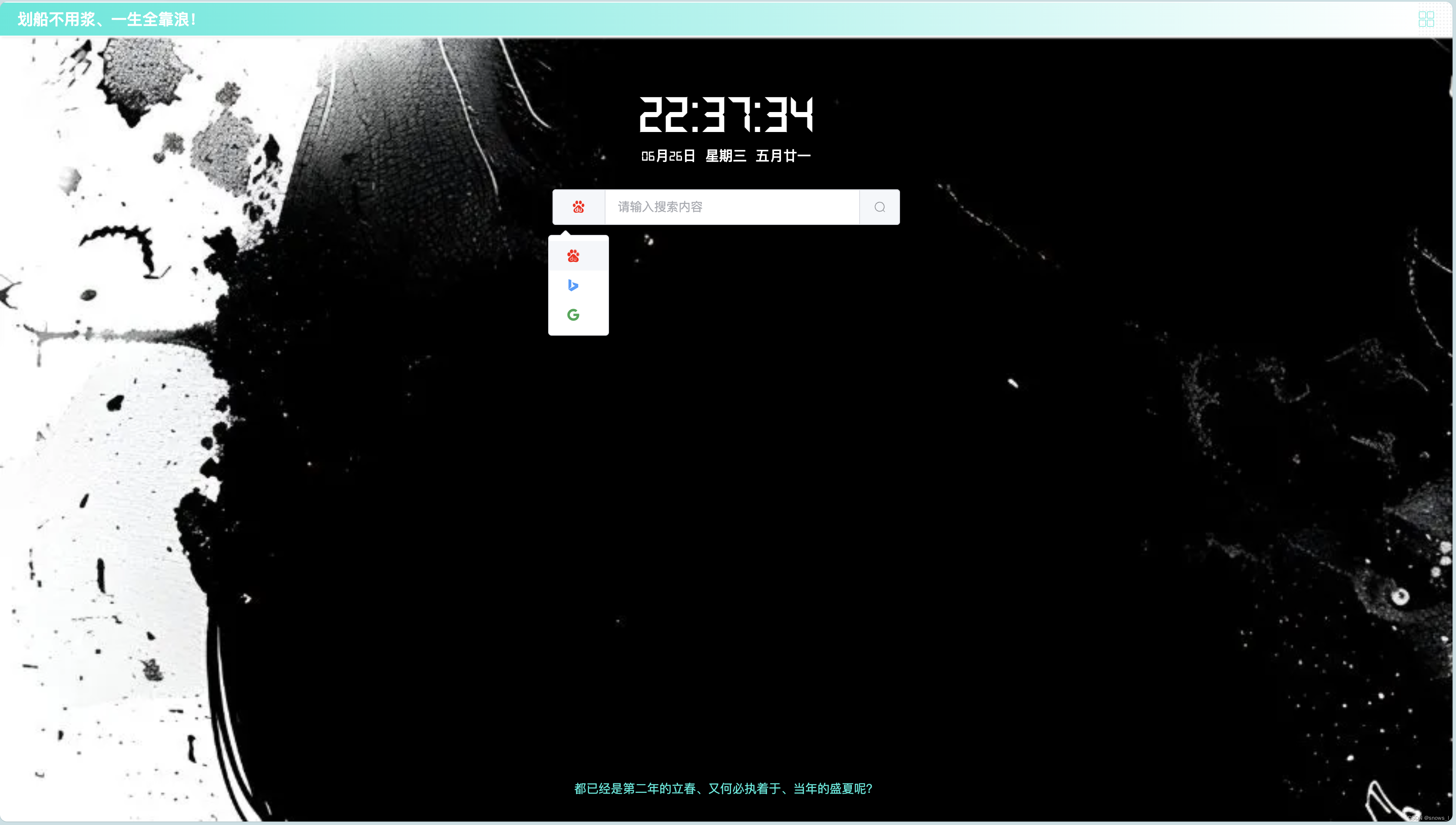
基于 elementUI / elementUI plus,实现 主要色(主题色)的一件换色(换肤)
一、效果图 二、方法 改变elementUI 的主要色 --el-color-primary 为自己选择的颜色,核心代码如下: // 处理主题样式 export function handleThemeStyle(theme) {document.documentElement.style.setProperty(--el-color-primary, theme) } 三、全部代…...

js 计算某个日期加月份最后月份不会增加或者跳变
/** * * param {*} dateString 原来日期 2023-12-31 * param {*} months 加月份 2 * returns 2024-02-29 */ export function getDateByMonth(dateString, months0) { console.log(1); let oldMonths dateString.substring(0,7); let day dateString.substring(8); let …...

Git简介与详细教程
一、简介 什么是Git? Git是一款分布式版本控制系统,由Linux之父Linus Torvalds于2005年开发。它旨在快速、高效地处理从小型到大型项目的所有内容。Git与传统的版本控制系统相比,具备显著的优势,主要体现在其分布式架构、强大的…...
创建OpenWRT虚拟机
环境:Ubuntu 2204,VM VirtualBox 7.0.18 安装必备软件包: sudo apt update sudo apt install subversion automake make cmake uuid-dev gcc vim build-essential clang flex bison g gawk gcc-multilib g-multilib gettext git libncurses…...

智慧安防新篇章:如何科学设定可燃气体报警器校准检测周期
随着科技的快速发展,智慧安防系统已成为现代社会不可或缺的一部分。在各类安全监测设备中,可燃气体报警器因其对潜在危险的及时预警功能而备受关注。 接下来,佰德将围绕可燃气体报警器的校准检测周期进行深入探讨,以确保其在智慧…...

如何优化Spring Boot应用的启动时间
如何优化Spring Boot应用的启动时间 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将讨论如何优化Spring Boot应用的启动时间,提升应用的性…...

(Effective C) 2.3 作用域
(Effective C) 2.3 作用域 文章目录 (Effective C) 2.3 作用域前言🔢4大作用域1️⃣文件作用域2️⃣块作用域3️⃣函数原型作用域4️⃣函数作用域 ⭐作用域性质📖实例CodeEND关注我 前言 作用域应用于标识符的某个特定声明。 标识符包含对象࿰…...
Python 基础 (标准库):堆 heap
1. 官方文档 heapq --- 堆队列算法 — Python 3.12.4 文档 2. 相关概念 堆 heap 是一种具体的数据结构(concrete data structures);优先级队列 priority queue 是一种抽象的数据结构(abstract data structures)&…...
代码实践 -卷积神经网络-30Kaggle竞赛:图片分类)
动手学深度学习(Pytorch版)代码实践 -卷积神经网络-30Kaggle竞赛:图片分类
30Kaggle竞赛:图片分类 比赛链接: https://www.kaggle.com/c/classify-leaves 导入包 import torch import torchvision from torch.utils.data import Dataset, DataLoader from torchvision import transforms import numpy as np import pandas as…...

【LeetCode】每日一题:数组中的第K大的元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 解题思路 第一种是快排,快…...
安装)
Keil5.38ARM,旧编译器(V5)安装
站内文章KEIL5MDK最新版(3.37)安装以及旧编译器(V5)安装_keil5 mdk-CSDN博客...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
