数据结构之二叉树的超详细讲解(3)--(二叉树的遍历和操作)
个人主页:C++忠实粉丝
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C++忠实粉丝 原创数据结构之二叉树的超详细讲解(3)--(二叉树的遍历和操作)
收录于专栏【数据结构初阶】
本专栏旨在分享学习数据结构学习的一点学习笔记,欢迎大家在评论区交流讨论💌
目录
1.前置说明
2.二叉树的遍历
2.1 前序、中序以及后序遍历
代码实现:
2.1.1前序遍历:
2.1.2中序遍历:
2.1.3后序遍历:
力扣oj练习
2.2 层序遍历
代码实现:
练习:
3.结点个数以及高度等
3.1二叉树节点个数
3.2二叉树叶子节点个数
3.3二叉树第k层节点个数
3.4二叉树查找值为x的节点
3.5二叉树的高度
4.二叉树的创建和销毁
4.1通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
4.2二叉树销毁
4.3判断二叉树是否时完全二叉树
1.前置说明
如果没看树和二叉树的结构和概念建议先去看看
----数据结构之二叉树的超详细讲解(1)--(树和二叉树的概念和结构)-CSDN博客
---数据结构之二叉树的超详细讲解(2)--(堆的概念和结构的实现,堆排序和堆排序的应用)-CSDN博客
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树 操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
二叉树的结构表示:
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
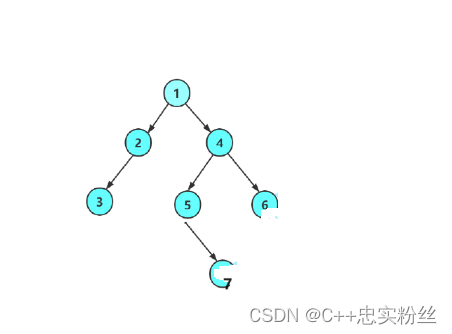
手动创造一棵树:
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node5->right = node7;return node1;
}将创造树节点的方法封装成一个函数(BuyNode):
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}这样我们就完成了一棵树的创建,如下图所示:
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
1. 空树
2. 非空:根结点,根结点的左子树、根结点的右子树组成的。
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
2.二叉树的遍历
2.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
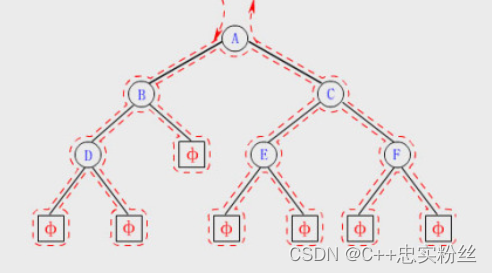
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
示例:
假如我们的二叉树为:

前序遍历:
前序遍历即访问根结点的操作发生在遍历其左右子树之前。也就是先访问根节点在访问左右子树,简称为根左右
所以前序遍历为: 1 2 3 NULL NULL NULL 4 5 NULL 6 NULL NULL
中序遍历:
中序遍历即访问左节点的操作发生在遍历其根节点和右节点之前,也就是先访问左节点在访问根右,简称左根右
所以中序遍历为:NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
后序遍历:
后序遍历即先访问左节点,在访问右节点和根节点,简称左右根
所以后序遍历为:NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
代码实现:
我们之前已经手动创建了一棵树:

2.1.1前序遍历:
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}我们这里的逻辑为:首先判断节点是否为空,为空即返回NULL(这里N就代表为NULL),并return,注意:这里的return并不是直接退出,而是返回函数上一层,不为空即直接打印节点data值,然后递归左右子树,满足根左右的性质.
结果如下:

递归展开图:
这里怕宝子们还是不理解递归的原理,这里就展示前序的递归展开图,中序和后序是一样的
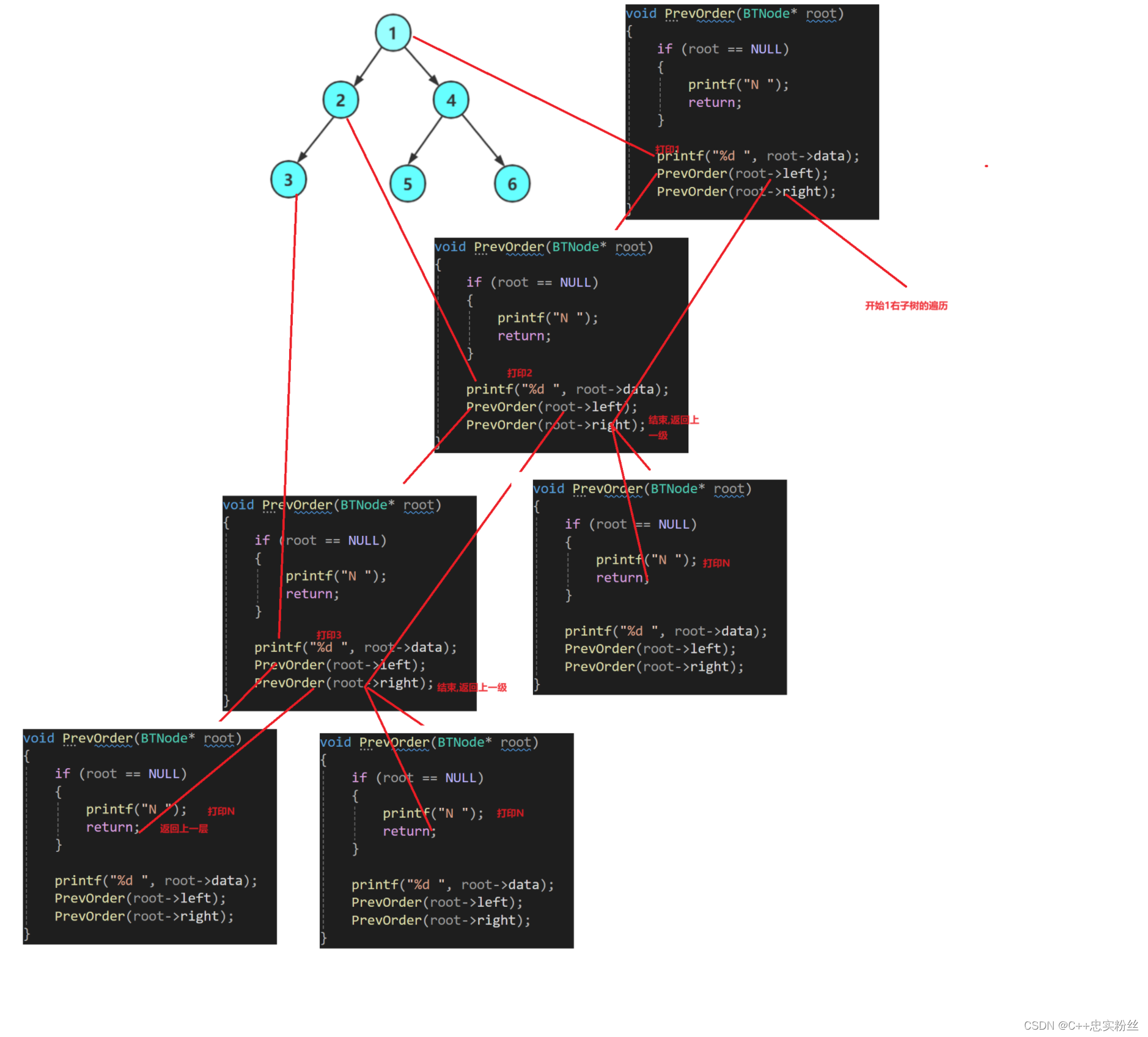 由于篇幅有限,没有完全展示,但是原理都是一样的
由于篇幅有限,没有完全展示,但是原理都是一样的
2.1.2中序遍历:
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}我们这里的逻辑和前序方法差不多,也是使用递归,满足左根右的性质进行后序遍历
结果如下:
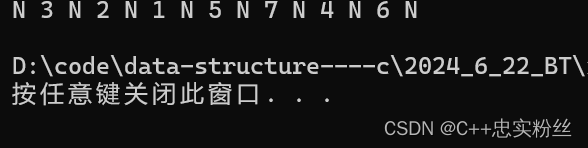
2.1.3后序遍历:
void postorder(BTNode* root)
{if (root == NULL){printf("N ");return;}postorder(root->left);postorder(root->right);printf("%d ", root->data);
}结果如下:
力扣oj练习
--144. 二叉树的前序遍历 - 力扣(LeetCode)
--94. 二叉树的中序遍历 - 力扣(LeetCode)
--145. 二叉树的后序遍历 - 力扣(LeetCode)
只要能把上面的知识看懂弄明白,这三个题目能很轻松的做出来.大家去看二叉树经典OJ练习-CSDN博客,里面进行了详细的讲解.
2.2 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根结点所在 层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层 上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
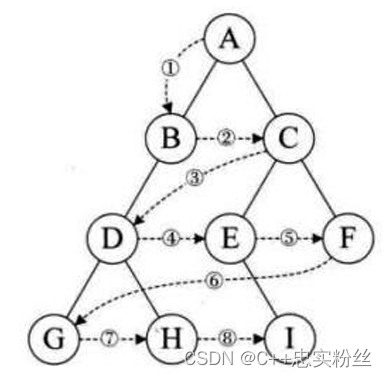
上图层序遍历的结果为:A B C D E F G H I
代码实现:
void TreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}QueueDestroy(&q);
}具体步骤:
初始化队列:
初始化一个队列并将根节点入队。如果根节点为空,则直接跳过。
层序遍历:
使用队列进行层序遍历。每次取出队列中的节点,打印节点的值,并将该节点的左右子节点分别入队。
清理资源:
销毁队列,释放资源。
这里需要用到队列的知识,使其能一层一层的遍历二叉树,对队列还不清楚的宝子们,可以看看下面的博客--数据结构之队列的超详细讲解-CSDN博客
练习:
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(A )
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK; 中序遍历:HFIEJKG.则二叉树根结点为(A)
A E
B F
C G
D H
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为__D__。
A adbce
B decab
C debac
D abcde
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列A
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
解答:
1. 完全二叉树按层次输出的序列为 ABCDEFGH ,该完全二叉树的前序序列为(A)
根据完全二叉树的定义,给出的层次遍历序列 ABCDEFGH 可以直接构建出二叉树,其中:
- 根节点是 A
- 第二层是 B 和 C
- 第三层是 D, E, F, G
- 第四层是 H
从这个结构我们可以推导前序遍历:
- 前序遍历是根 -> 左子树 -> 右子树
- 根是 A
- 左子树的前序遍历是 B -> D -> H -> E
- 右子树的前序遍历是 C -> F -> G
因此,前序遍历是:
ABDHECFG答案是 A:ABDHECFG
2. 二叉树的先序遍历和中序遍历如下:
先序遍历:EFHIGJK; 中序遍历:HFIEJKG
从先序遍历可以看出根结点是 E。根据中序遍历,E 左边的部分是左子树,右边的部分是右子树:
- 中序遍历分割为: 左子树 HFI 和右子树 EJKG
- 按照先序遍历的顺序,E 后面的字符分别属于左子树和右子树:
- 左子树的先序遍历是 FHI
- 右子树的先序遍历是 JKG
所以,根结点是 E。
答案是 A:E
3. 二叉树的中序遍历序列:badce,后序遍历序列:bdeca
从后序遍历可以看出根结点是 a。根据中序遍历,a 左边的是左子树,右边的是右子树:
- 中序遍历分割为: 左子树 b 和右子树 dce
- 后序遍历的顺序,左子树的顺序是 b,右子树的顺序是 dec
前序遍历是根 -> 左子树 -> 右子树:
abcde答案是 D:abcde
4. 二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF
这意味着每个节点只有一个子节点,并且这些节点按顺序排列,如果它们按层次输出,那么最深的节点将排在最后。
如果后序遍历和中序遍历相同:
- 最右边的节点(即最后一个节点)是树的根节点
- 其余节点依次按照层次遍历的顺序向左添加
按层次遍历从根开始,从层次的最右边开始,因此应该是 F -> E -> D -> C -> B -> A
答案是 A:FEDCBA
3.结点个数以及高度等
3.1二叉树节点个数
这里大家很容易写出错误代码,比如:
int TreeSize(BTNode* root)
{int size = 0;if (root == NULL)return 0;else++size;TreeSize(root->left);TreeSize(root->right);return size;
}这段代码看起来非常好理解,相当于进行了一次前序遍历,将遍历的节点进行返回.
在这个函数中,size 是一个局部变量,每次调用 TreeSize 时都会重新初始化为 0。让我们逐步分析一下这个函数的行为。
分析:
-
当
root == NULL时,函数直接返回 0。这是树为空的情况。 -
如果
root不为NULL:int size = 0;初始化size为 0。++size;将size增加 1,所以size现在为 1。
-
然后递归调用
TreeSize(root->left)和TreeSize(root->right),但是这些调用的返回值并没有被使用或累加到size上。 -
因此,无论左右子树中有多少节点,这些递归调用的结果都不会影响当前函数中的
size变量。每次递归调用都会在自己的栈帧中初始化一个新的size变量,并且最终返回 1 或 0。
函数递归展开图:

用static进行改进:
int TreeSize(BTNode* root)
{static int size = 0;if (root == NULL)return 0;else++size;TreeSize(root->left);TreeSize(root->right);return size;
}
static变量在整个程序运行期间只会被初始化一次,这样就避免了局部变量一直的初始化
结果如下:
 结果是没有问题的,可是当我们多次调用呢?
结果是没有问题的,可是当我们多次调用呢?
这里我重复调用三次:

结果如下:

正是因为
static变量在整个程序运行期间只会被初始化一次,所以如果你多次用TreeSize函数,size会一直累积之前的计算结果,而不会重新开始计算新的树的大小。
正确代码:
int TreeSize(BTNode* root)
{return root == NULL ? 0 :TreeSize(root->left) + TreeSize(root->right) + 1;
}为了修正这些问题,可以将递归调用的结果累加到
size中,并将最终的size值作为函数的返回值。
函数递归展开图:

这段代码利用递归的方式计算二叉树的节点总数,通过递归遍历所有节点,实现了对整个二叉树的全面统计。递归的基准情况是遇到空节点返回 0,而在非空节点情况下,递归地计算左右子树的大小并进行累加,从而获得整棵树的节点总数。
3.2二叉树叶子节点个数
补充一下什么是叶子节点:
没有子树的节点叫做叶子节点,也称度为0的节点
代码展示:
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left)+ TreeLeafSize(root->right);
}分析
基准情况:
- 如果
root为NULL,则树为空,没有叶节点。因此,返回 0。叶节点情况:
- 如果
root的左子节点和右子节点都为NULL,那么当前节点为叶节点。因此,返回 1。递归情况:
- 如果当前节点不是叶节点,则递归计算其左、右子树中的叶节点数量,并将它们加起来。
- 通过递归调用
TreeLeafSize(root->left)和TreeLeafSize(root->right)来分别计算左、右子树中的叶节点数量,并将结果相加。
递归展开图:
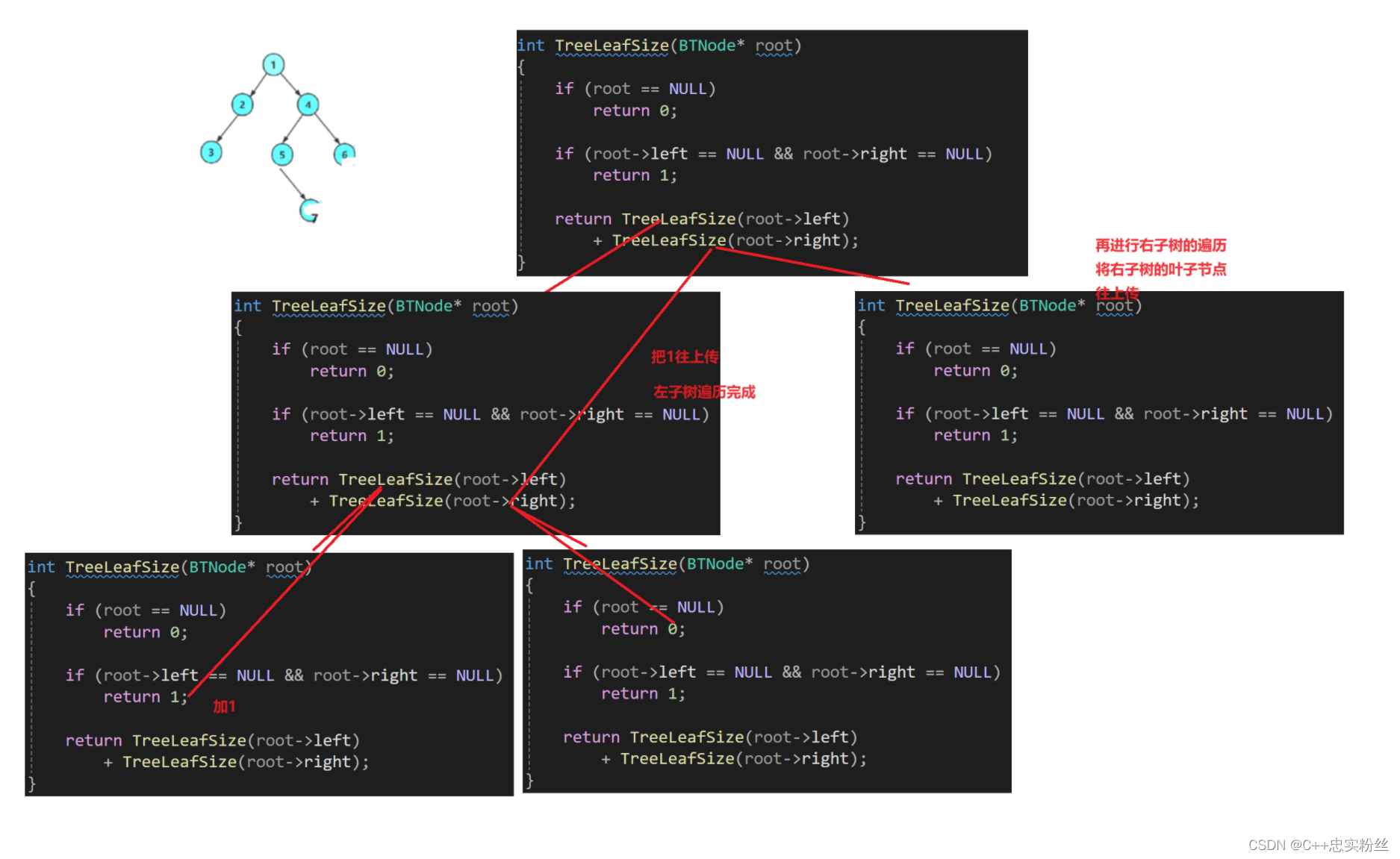
结果如下:
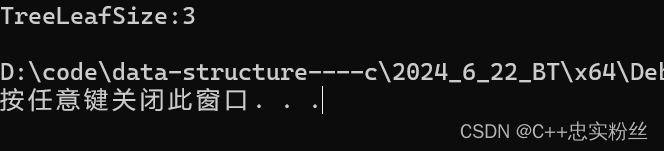
结果为3,没有问题
3.3二叉树第k层节点个数
代码展示:
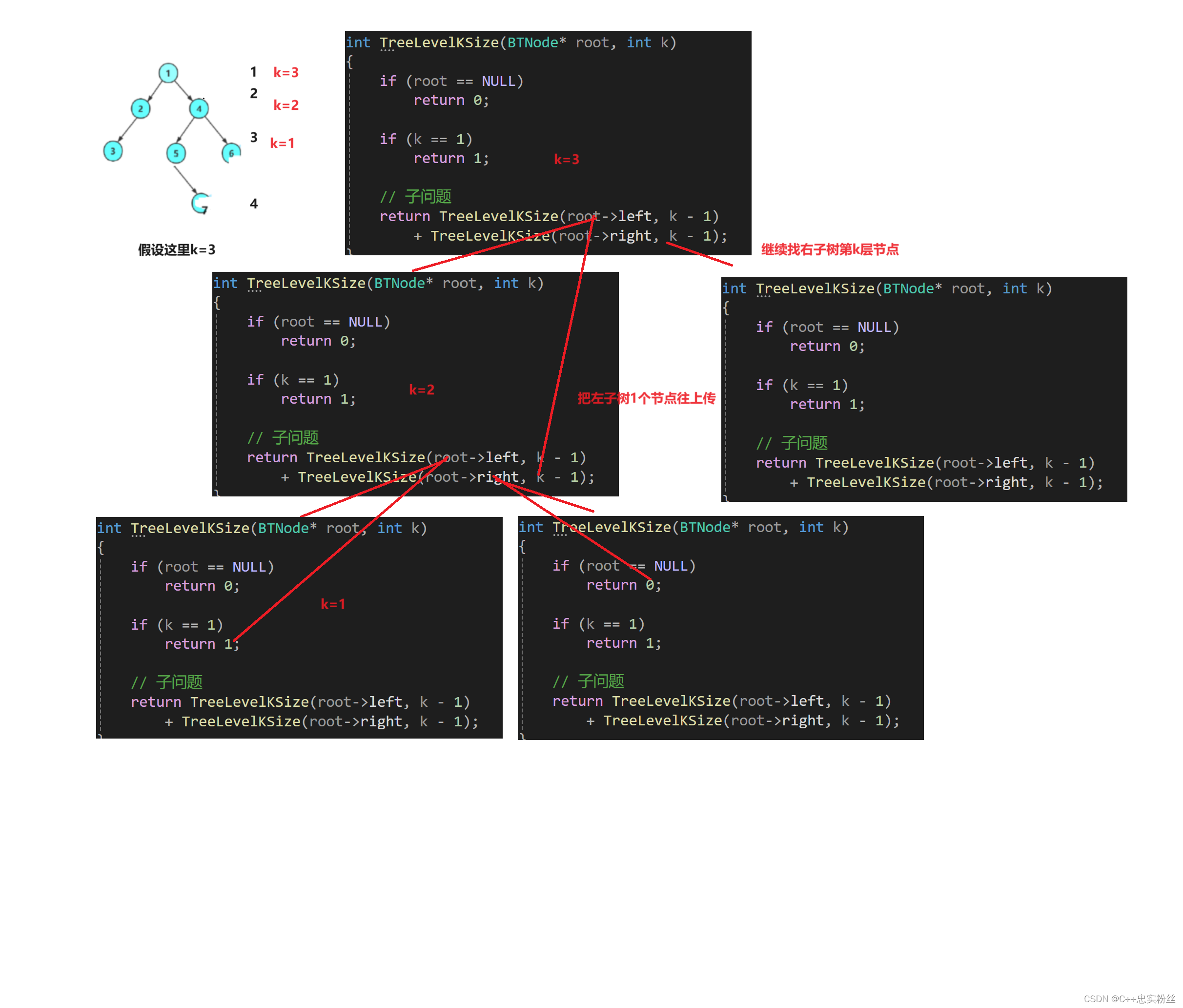
int TreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;// 子问题return TreeLevelKSize(root->left, k - 1)+ TreeLevelKSize(root->right, k - 1);
}函数递归展开图:
分析
基础情况处理:
if (root == NULL) return 0;:如果当前节点root为空,则返回 0。这是递归的终止条件之一,表示空节点没有子节点,因此在任何层级上都没有节点。
if (k == 1) return 1;:当k等于 1 时,表示已经递归到目标层级。根据题设,每个节点自身被视为一个层级,因此返回 1。递归调用:
return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);如果当前节点root不为空且k > 1,则递归调用TreeLevelKSize函数来计算左子树和右子树中第k-1层级的节点数目。最终返回的是左子树第k-1层级节点数目和右子树第k-1层级节点数目的和。
3.4二叉树查找值为x的节点
代码展示:
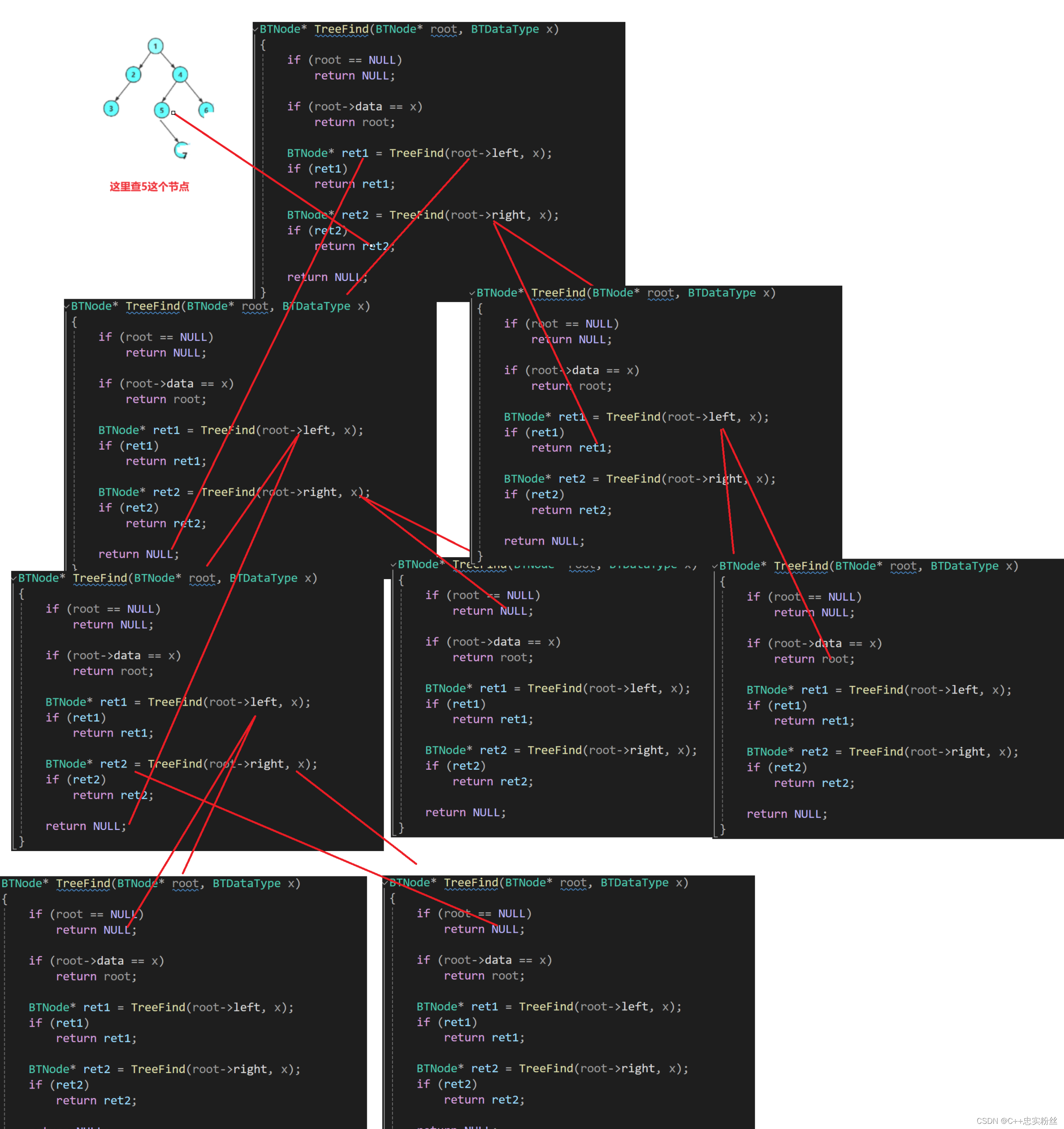
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* ret1 = TreeFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = TreeFind(root->right, x);if (ret2)return ret2;return NULL;
}函数递归展开图:
分析
基础情况处理:
if (root == NULL) return NULL;:如果当前节点root为空,则直接返回NULL,表示未找到目标节点。
if (root->data == x) return root;:如果当前节点的值等于x,则返回当前节点root,表示已找到目标节点。递归查找:
BTNode* ret1 = TreeFind(root->left, x);
- 递归在左子树中查找值为
x的节点。如果找到了(即ret1不为NULL),直接返回ret1。
BTNode* ret2 = TreeFind(root->right, x);
- 如果左子树中未找到目标节点,继续递归在右子树中查找值为
x的节点。如果找到了(即ret2不为NULL),直接返回ret2。返回结果:
- 如果在当前节点及其左右子树中都未找到值为
x的节点,则返回NULL,表示整棵树中没有该节点。
3.5二叉树的高度
代码一:
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return TreeHeight(root->left) > TreeHeight(root->right) ?TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}分析
基准情况:
- 如果
root为NULL,则树为空,高度为 0。因此,返回 0。递归情况:
- 如果当前节点不为空,则递归计算其左、右子树的高度,并返回较大的那个值加上 1。
- 通过递归调用
TreeHeight(root->left)和TreeHeight(root->right)来分别计算左、右子树的高度。- 使用条件运算符
? :来比较左、右子树的高度,并将较大的那个值加上 1 返回。
这个解法是没有问题的,但是它的时间效率不高,它在递归过程中有的值会重复计算多次
函数递归展开图:
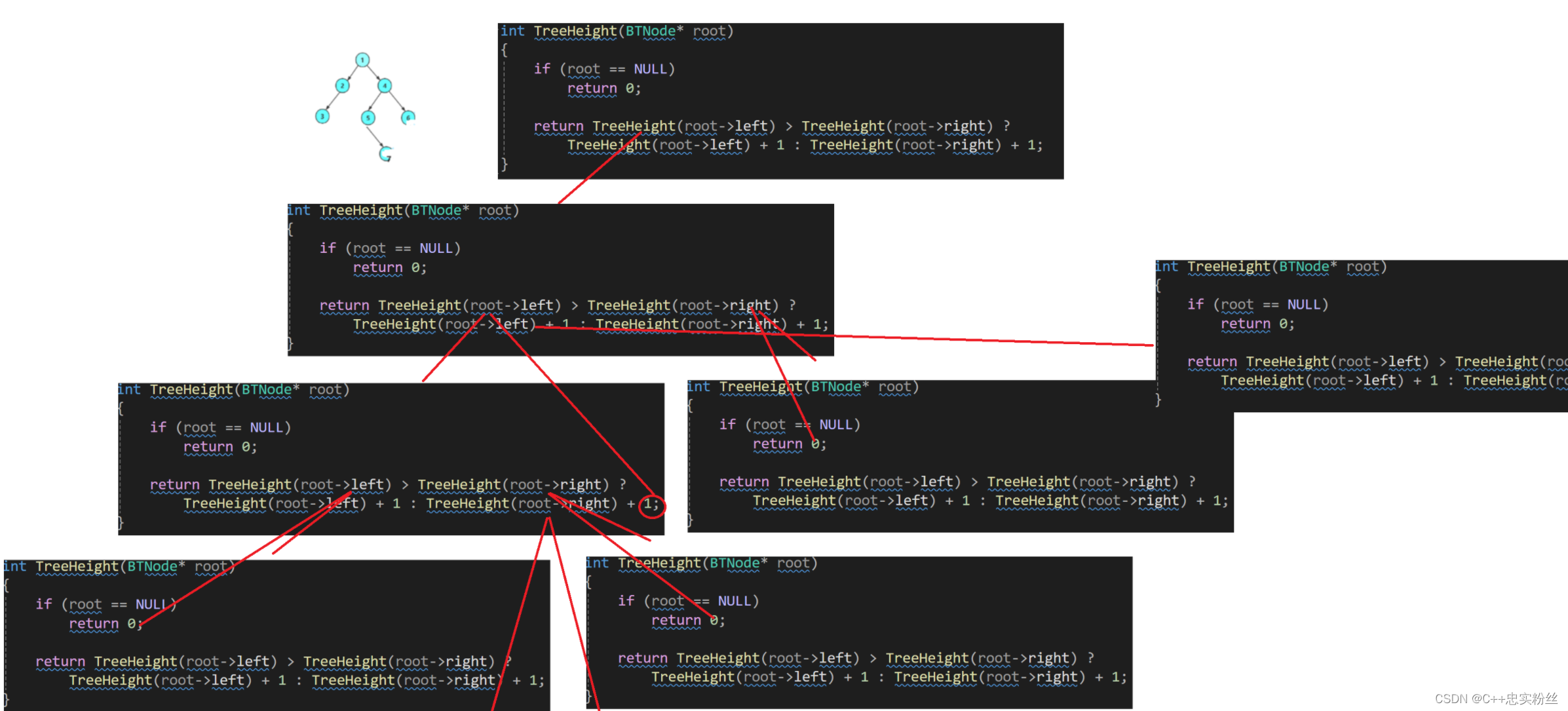
我们可以看到,我们每次计算出左右子树的高度后,并不会进行记录,导致我们比较完成后还需要进行递归计算,导致效率不高
代码二:
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}函数递归展开图:

可以发现我们用两个变量存储之后,每次我们都只需要一次,避免了重复计算,提高了时间效率
这里大家可以试一试,在力扣上面右一道计a算二叉树的深度,如果你使用第一种代码,只通过了35个例子,超时了,因为后面的例子数据庞大,如果你使用第一种方案,最低层的值会被重复计算很多次,导致超出时间限制
而我们用第二种方法,能很顺利的通过

下面是原题链接:
--LCR 175. 计算二叉树的深度 - 力扣(LeetCode)
4.二叉树的创建和销毁
4.1通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
代码展示:
BTNode* CreateTree(char* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->data = a[(*pi)++];root->left = CreateTree(a, pi);root->right = CreateTree(a, pi);return root;
}函数递归展开图:
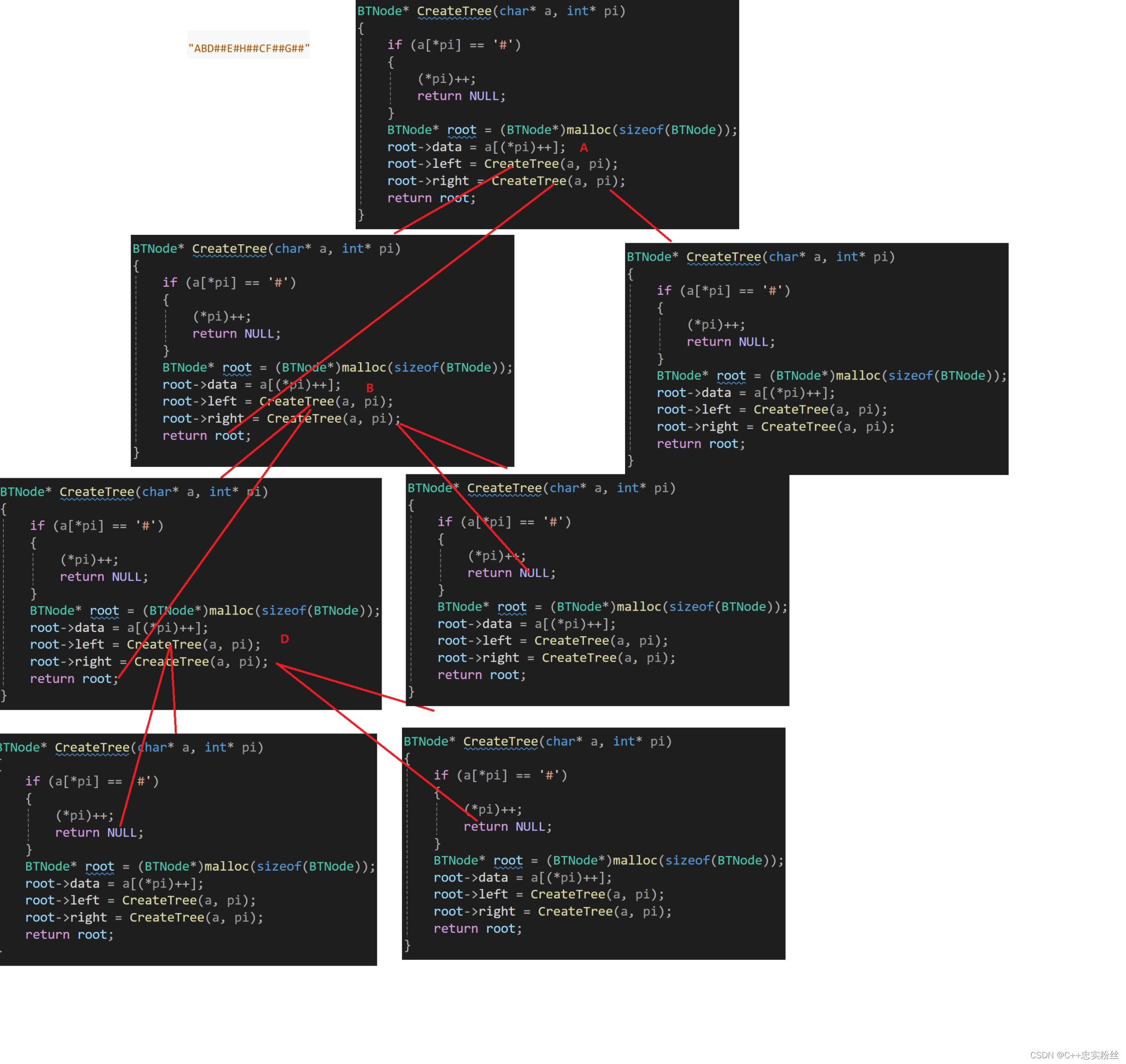
函数分析:
参数:
char* a:存储先序遍历序列的字符数组,包含节点的数据和 '#' 表示的空节点。int* pi:指向当前处理的字符在数组a中的索引的指针。返回值:
BTNode*:返回值是指向根节点BTNode结构体的指针。递归过程:
- 如果当前字符是
'#',表示遇到空节点,函数会返回NULL,并且将指针pi向后移动一位。- 如果当前字符不是
'#',则创建一个新的节点,将当前字符作为节点的数据,并将指针pi向后移动一位。- 然后递归调用
CreateTree函数来构建左子树和右子树,分别将它们赋给当前节点的left和right指针。返回根节点:
- 最后返回根节点的指针。
4.2二叉树销毁
代码展示:
// 二叉树销毁
void TreeDestory(BTNode* root)
{if (root == NULL)return;TreeDestory(root->left);TreeDestory(root->right);free(root);
}函数递归展开图:
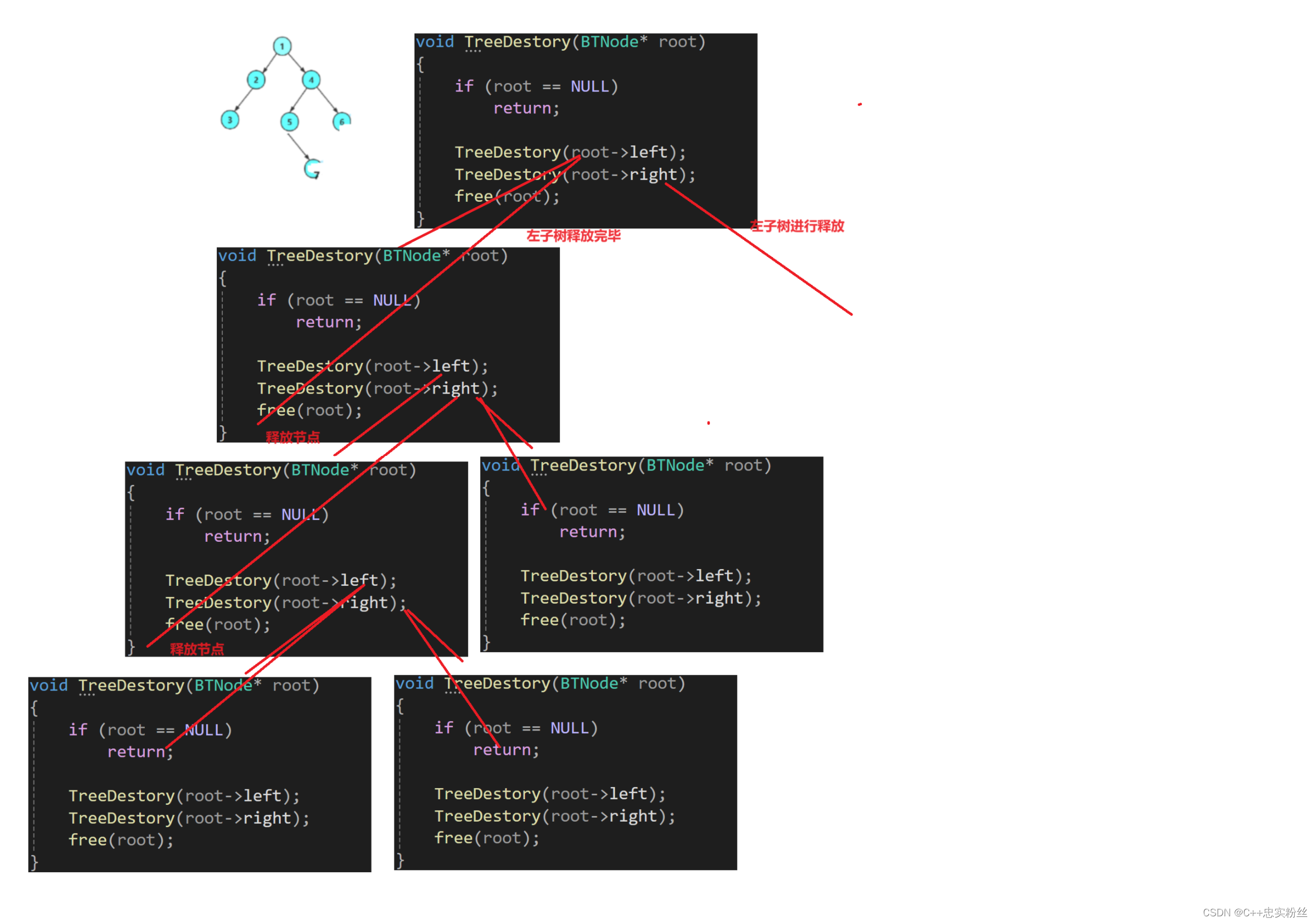
函数分析:
检查根节点是否为空:
- 如果传入的根节点
root为NULL,说明树为空或者已经到达叶子节点的子节点(即空节点),直接返回,不进行任何操作。递归销毁左子树:
- 调用
TreeDestory(root->left)递归地销毁左子树。此调用会一直递归到最左子节点,然后逐级返回并销毁每个节点。递归销毁右子树:
- 调用
TreeDestory(root->right)递归地销毁右子树。此调用会一直递归到最右子节点,然后逐级返回并销毁每个节点。释放当前节点的内存:
- 在左右子树都被销毁后,最后释放当前节点的内存
free(root)。
4.3判断二叉树是否时完全二叉树
代码展示:
// 判断二叉树是否是完全二叉树
bool TreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 遇到第一个空,就可以开始判断,如果队列中还有非空,就不是完全二叉树if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 如果有非空,就不是完全二叉树if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}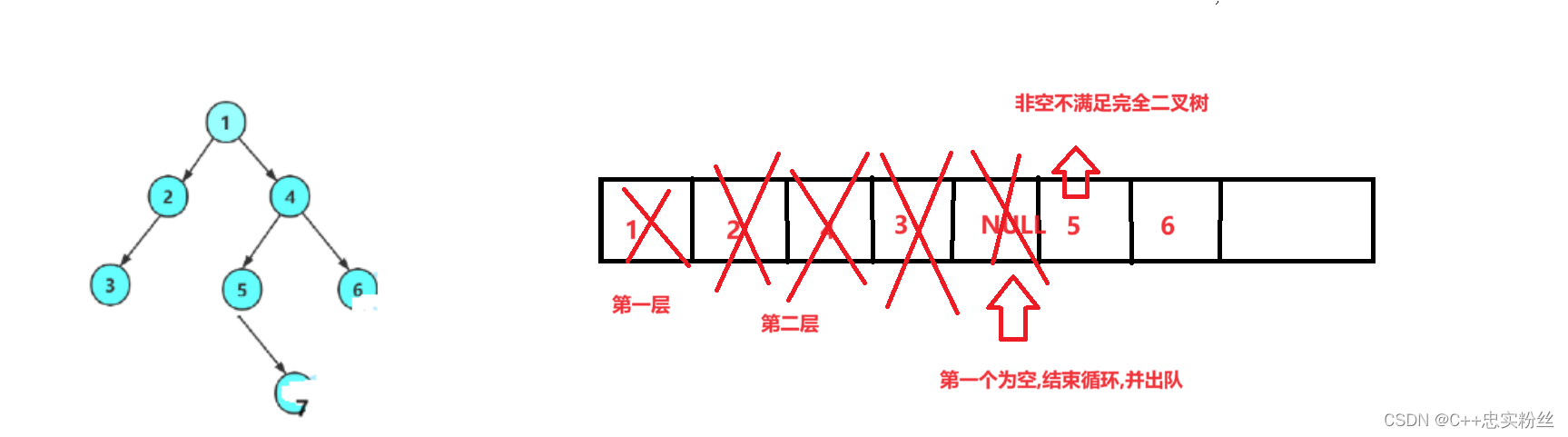
具体步骤:
初始化队列:
初始化一个队列并将根节点入队。如果根节点为空,则直接跳过。
层序遍历:
使用队列进行层序遍历。每次取出队列中的节点,如果遇到空节点(
NULL),则退出该循环。否则,将该节点的左右子节点分别入队。检测后续节点:
继续检查队列中剩余的节点。如果存在非空节点,则树不是完全二叉树,返回
false。否则,继续检查直到队列为空。清理与返回:
销毁队列,释放资源,并返回
true表示该二叉树是完全二叉树。
相关文章:

数据结构之二叉树的超详细讲解(3)--(二叉树的遍历和操作)
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 数据结构之二叉树的超详细讲解(3)--(二叉树的遍历和操作) 收录于专栏【数据结构初阶】 本专栏旨在分享学习数据结构学习的一点学习笔记,欢迎大家在评…...
Arduino - 旋转编码器 - 伺服电机
Arduino - 旋转编码器 - 伺服电机 Arduino - Rotary Encoder In this tutorial, We are going to learn how to program Arduino to rotate a servo motor according to the rotary encoder’s output value. 在本教程中,我们将学习如何对Arduino进行编程ÿ…...

儿童电动音乐牙刷OTP芯片方案:NV040C,耐温耐压,抗干扰能力强
一:方案背景概述 随着科技的飞速发展,源于对儿童口腔健康深入细致的关怀,以及对现代科技在日常生活用品中应用的不断追求,儿童电动音乐牙刷OTP芯片方案的诞生。 二:芯片简介 NV040C语音芯片是一款性能稳定、适合工厂量…...
Sentinel链路流控模式失效的解决方法
解决方法 1、在pom.xml中增加sentinel-web-servlet的依赖,我使用的版本是1.7.1 <dependency><groupId>com.alibaba.csp</groupId><artifactId>sentinel-web-servlet</artifactId> </dependency>2、在项目中添加一个FilterCon…...
Web应用安全测试-专项漏洞(一)
Web应用安全测试-专项漏洞(一) 专项漏洞部分注重测试方法论,每个专项仅列举一个例子。实际测试过程中,需视情况而定。 文章目录 Web应用安全测试-专项漏洞(一)Web组件(SSL/WebDAV)漏…...
VMware ESXi 8.0U2c macOS Unlocker OEM BIOS Huawei (华为) FusionServer 定制版
VMware ESXi 8.0U2c macOS Unlocker & OEM BIOS Huawei (华为) FusionServer 定制版 ESXi 8.0U2 标准版,Dell (戴尔)、HPE (慧与)、Lenovo (联想)、Inspur (浪潮)、Cisco (思科)、Hitachi (日立)、Fujitsu (富士通)、NEC (日电)、Huawei (华为)、xFusion (超聚…...

python中的高阶函数介绍
在Python中,高阶函数是指那些可以接受函数作为参数或者返回函数作为结果的函数。这种特性使得函数式编程成为可能,并且可以编写出更加简洁和灵活的代码。以下是Python中一些常用的高阶函数: map() map() 函数接受一个函数和一个可迭代对象作为…...

华为OD机试 - 石头剪刀布游戏(Java 2024 D卷 200分)
华为OD机试 2024D卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(D卷C卷A卷B卷)》。 刷的越多,抽中的概率越大,每一题都有详细的答题思路、详细的代码注释、样例测…...

[开发|java] LocalDate转化为LocalDateTime
要将 java.time.LocalDate 转换为 java.time.LocalDateTime,你需要指定一天中的时间。因为 LocalDate 只包含日期部分(年、月、日),而 LocalDateTime 包含日期和时间(时、分、秒、纳秒),所以在转…...

介绍几种 MySQL 官方高可用方案
前言: MySQL 官方提供了多种高可用部署方案,从最基础的主从复制到组复制再到 InnoDB Cluster 等等。本篇文章以 MySQL 8.0 版本为准,介绍下不同高可用方案架构原理及使用场景。 1.MySQL Replication MySQL Replication 是官方提供的主从同…...
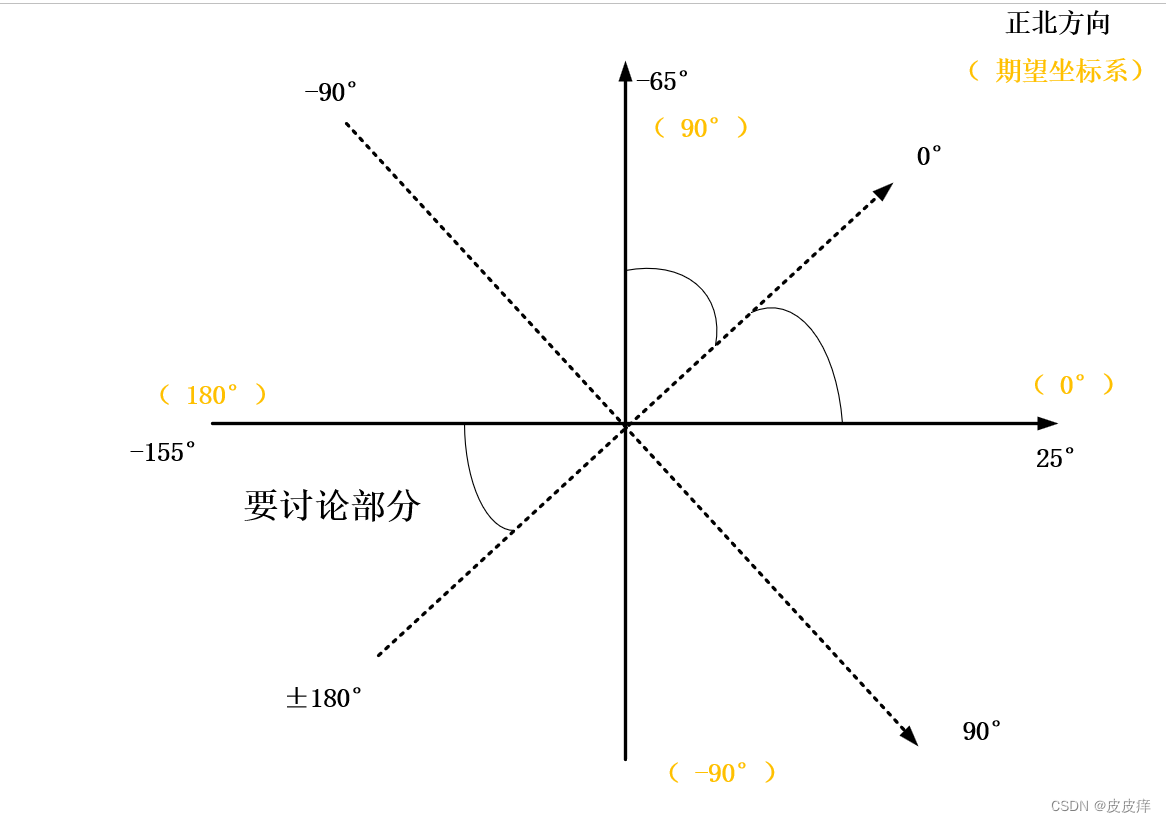
IMU坐标系与自定义坐标系转化
1.首先示例图为例: 虚线黑色角度为IMU的坐标系;实线为自定义坐标系; 矫正:(默认angleyaw为IMU采的数据角度) angleyaw_pt angleyaw-25;if(-180<angleyaw&&angleyaw<-155) // 角度跳变问…...
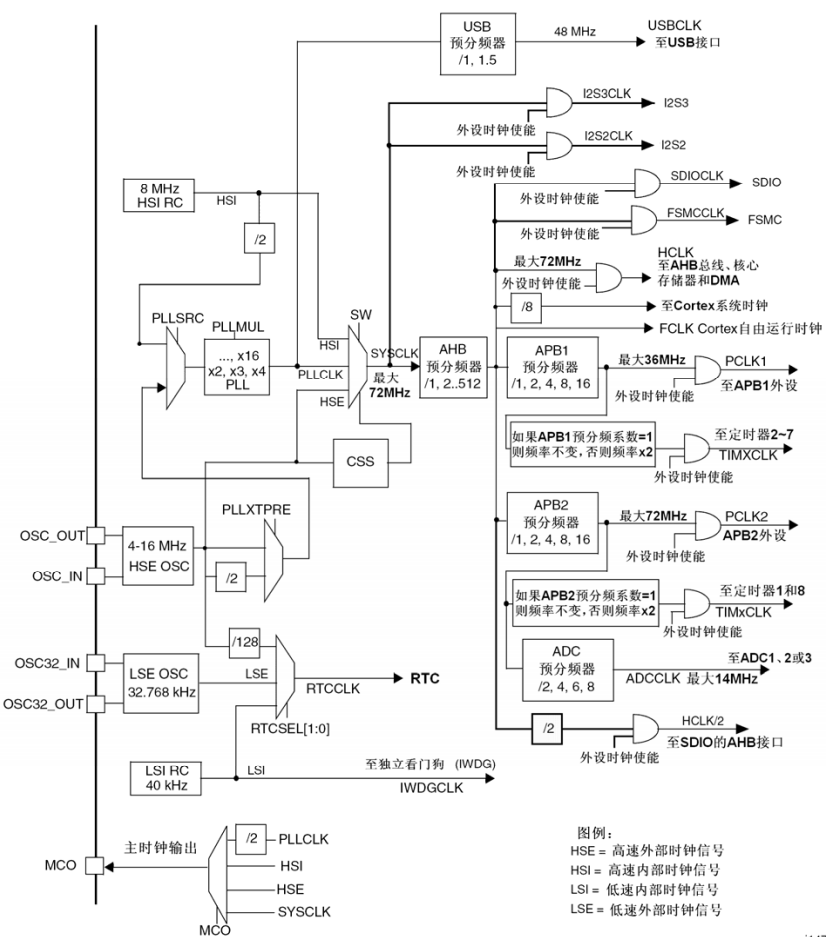
《STM32 HAL库》RCC 相关系列函数详尽解析—— HAL_RCC_OscConfig()
观前提示:函数完整代码在文末,本文梳理了函数HAL_RCC_OscConfig()的主要逻辑和实现方法f105时钟树详解图 HAL_RCC_OscConfig() 函数介绍: 此函数是一个用于初始化RCC(Reset and Clock Control)振荡器(Osc…...
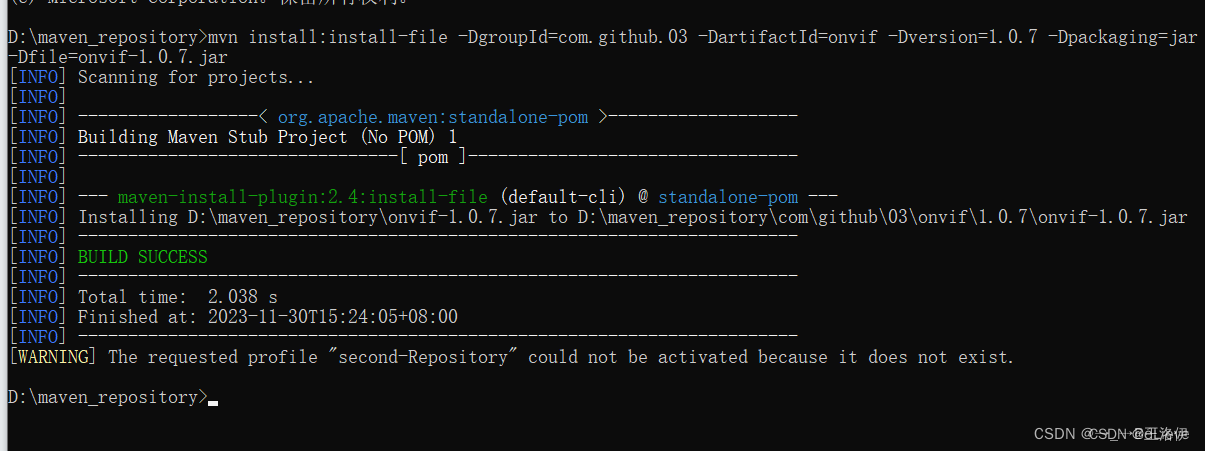
手动将jar包导入本地Maven仓库
1、进入存放jar包的目录,可以先放进仓库底下 2、cmd回车 3、执行命令,看到BUILD SUCCESS就是成功了 -DgroupId、-DartifactId、-Dversion、-Dfile记得换成自己对应的 mvn install:install-file -DgroupIdcom.github.03 -DartifactIdonvif -Dversion1.0…...

煤安防爆手机为什么能在煤矿井下使用
煤安防爆手机之所以能在煤矿井下使用,是因为它们经过特殊设计,符合严格的防爆安全标准,能够防止电火花引发爆炸,同时具备防尘防水、抗冲击等特性,确保在恶劣的煤矿环境中稳定可靠地运行,为工作人员提供安全…...

科普小课堂|不同版本USB接口详细解析
USB接口凭借其广泛的兼容性和高性能,已成为连接多样外设的主要接口,囊括了日常的键盘、鼠标等输入设备以及其他更多的领域。不仅如此,USB还展现了高度灵活性,能够便捷地转换为其他总线接口,例如实现USB到以太网或USB到…...

Spring Boot中的JSON解析优化
Spring Boot中的JSON解析优化 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨在Spring Boot应用中如何优化JSON解析,以提升系统的性能…...

全彩屏负氧离子监测站
TH-FZ5在追求绿色生态、健康出行的今天,景区不仅仅是人们休闲游玩的好去处,更是人们体验大自然、感受清新空气的重要场所。为了进一步提升游客的游览体验,许多景区纷纷引入了全彩屏负氧离子监测站,这一创新举措不仅为景区增添了科…...

LeetCode 1207.独一无二的数
题目要求 给你一个整数数组 arr,请你帮忙统计数组中每个数的出现次数。如果每个数的出现次数都是独一无二的,就返回 true;否则返回 false。示例 1:输入:arr [1,2,2,1,1,3] 输出:true 解释:在该…...
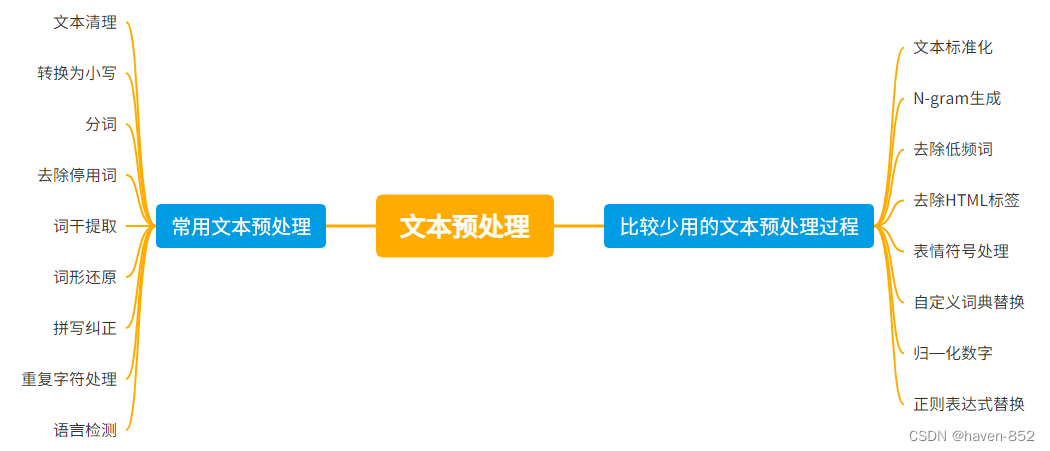
自然语言处理——英文文本预处理
高质量数据的重要性 数据的质量直接影响模型的性能和准确性。高质量的数据可以显著提升模型的学习效果,帮助模型更准确地识别模式、进行预测和决策。具体原因包括以下几点: 噪音减少:高质量的数据经过清理,减少了无关或错误信息…...
2024年二级建造师机电工程专业历年考试题库精选答案解析。
1.根据《标准施工招标文件》,关于施工合同变更权和变更程序的说法,正确的是()。 A.发包人可以直接向承包人发出变更意向书 B.承包人书面报告发包人后,可根据实际情况对工程进行变更 C.承包人根据合同约定࿰…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
