一种改进解卷积算法在旋转机械故障诊断中的应用(MATLAB)
轴承振动是随机振动。在不同的时刻,轴承振动值是不尽相同的,不能用一个确定的时间函数来描述。这是由于滚动体除了有绕轴承公转运动以外,还有绕自身轴线的自旋运动,且在轴承运转时,滚动接触表面形貌是不断变化的,以及外来杂质进入运行区域的不确定性形成的。轴承振动也是宽带振动,其振动能量分布在一个宽带范围内,反映在幅值谱中就是轴承的振动频率范围为零到数万赫兹的连续谱。
当轴承正常时,其振动信号近似服从正态分布,此时信号中非噪声成分主要源于保持架转频和轴频,以及保持架对轴的旋转产生的微弱调制,信号能量在频域分布比较均匀,且各个频率分量的不确定性都较大且比较接近;而当轴承出现故障时,故障冲击将激励系统共振,产生脉冲冲击串,这将改变轴承振动信号的概率分布和能量分布,信号能量就会逐渐集中到故障特征频率(带)上。且随着轴承性能退化,信噪水平增加,信号的频率分布变得越来越规则,轴承振动信号的能量也会更加集中。
当轴承故障时,其原始脉冲冲击信号受随机噪声信号和周期信号干扰,并经过一定的传递路径衰减等因素影响,传感器采集的振动信号往往不能够反映真实的轴承故障信息,为设备故障诊断和状态监测增加了难度。解卷积类算法可以突出信号中的脉冲冲击成分,使得滤波后信号是原来脉冲冲击成分的一个近似。因此,可以认为经解卷积滤波后的信号是一个更加接近于轴承脉冲冲击信号的信号,对该信号做包络谱分析等即可找出轴承故障频率,进而反映轴承的故障类型。而当轴承正常时,轴承的脉冲冲击信号主要为轴的转频成分。经解卷积滤波处理后的信号,其在包络谱中对应的峰值频率为轴的转频,为判断轴承正常提供理论依据。
鉴于此,采用一种改进解卷积算法对旋转机械进行故障诊断,该算法不需要先验知识,效果较好。
function [CoSi, Bm] = CoSiEn(Sig, varargin)narginchk(1,11)
Sig = squeeze(Sig);p = inputParser;
Chk = @(x) isnumeric(x) && isscalar(x) && (x > 0) && (mod(x,1)==0);
Chk2 = @(x) isnumeric(x) && isscalar(x) && (x >= 0);
Chk3 = @(x) isnumeric(x) && isscalar(x) && (x > 1) && (mod(x,1)==0);
addRequired(p,'Sig',@(x) isnumeric(x) && isvector(x) && (length(x) > 10));
addParameter(p,'m',2,Chk3);
addParameter(p,'tau',1,Chk);
addParameter(p,'r',.1,@(x) isnumeric(x) && (x > 0) && (x < 1));
addParameter(p,'Logx',2,Chk2);
addParameter(p,'Norm',0,@(x) ismember(x,[0:4]));
parse(p,Sig,varargin{:})
m = p.Results.m; tau = p.Results.tau; r = p.Results.r;
Logx = p.Results.Logx; Norm = p.Results.Norm;N = length(Sig);
if Logx == 0Logx = exp(1);
end
if Norm == 1Xi = Sig - median(Sig);
elseif Norm == 2Xi = Sig - mean(Sig);
elseif Norm == 3Xi = (Sig - mean(Sig))/std(Sig,1);
elseif Norm == 4Xi = (2*(Sig - min(Sig))/range(Sig)) - 1;
elseXi = Sig;
end
Nx = N-((m-1)*tau);
Zm = zeros(Nx,m);
for n = 1:mZm(:,n) = Xi((n-1)*tau+1:Nx+(n-1)*tau);
endNum = Zm*Zm';
Mag = sqrt(diag(Num));
Den = Mag*Mag';
AngDis = acos(Num./Den)/pi;
if max(imag(AngDis(:))) < (10^-5) %max(max(imag(AngDis))) < (10^-5)Bm = sum(sum(triu(round(AngDis,6) < r,1)))/(Nx*(Nx-1)/2);
elseBm = sum(sum(triu(real(AngDis) < r,1)))/(Nx*(Nx-1)/2);warning('Complex values ignored')
end
if Bm == 1 || Bm == 0CoSi = 0;
elseCoSi = -(Bm*log(Bm)/log(Logx)) - ((1-Bm)*log(1-Bm)/log(Logx));
end
end
代码可通过知乎学术咨询获得:
https://www.zhihu.com/consult/people/792359672131756032?isMe=1

擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
相关文章:

一种改进解卷积算法在旋转机械故障诊断中的应用(MATLAB)
轴承振动是随机振动。在不同的时刻,轴承振动值是不尽相同的,不能用一个确定的时间函数来描述。这是由于滚动体除了有绕轴承公转运动以外,还有绕自身轴线的自旋运动,且在轴承运转时,滚动接触表面形貌是不断变化的&#…...
:jedis基于Redis setnx、get、getset的分布式锁)
分布式锁(4):jedis基于Redis setnx、get、getset的分布式锁
1 实现原理 setnx(lockkey, 当前时间+过期超时时间) ,如果返回1,则获取锁成功;如果返回0则没有获取到锁,转向步骤(2)get(lockkey)获取值oldExpireTime ,并将这个value值与当前的系统时间进行比较,如果小于当前系统时间,则认为这个锁已经超时,可以允许别的请求重新获取,…...

linux内存排查工具smem使用
smem 是一个强大的工具,用于分析 Linux 系统中各进程的内存使用情况。-r 和 -k 选项用于指定输出格式和单位。以下是这两个选项的详细解析: -r:按照进程的内存使用量进行排序,默认按 RSS(常驻内存集)排序。-k:将输出的内存单位设为千字节(KB)。使用 smem 的命令示例 …...

云主机相比物理机有哪些优势
随着信息技术的飞速发展,云计算技术逐渐成为现代企业的核心驱动力。其中,云主机作为云计算的重要组成部分,以其高性能、高可用性和灵活便捷的特性,成为企业IT架构的新选择。今天我们就来了解探讨云主机相比传统主机,有…...
ClickHouse-Keeper安装使用
1.rpm 安装 clickhouse-keeper rpm -ivh clickhouse-keeper-23.8.11.28.x86_64.rpm 2.修改keeper的配置文件 vi /etc/clickhouse-keeper/keeper_config.xml修改部分参数 1.可修改日志等存储路径 2.增加监听配置 <listen_host>0.0.0.0</listen_host> 3.server_id…...

全国产飞腾+FPGA架构,支持B码+12网口+多串电力通讯管理机解决方案
GMSL 摄像头 GMSL 是 Maxim 公司推出的一种高速串行接口,适用于视频、音频和控制信号的传输,使用 50Ω 同轴电缆或 100Ω 屏蔽双绞线(STP)电缆时的距离可达 15m 或更长。 Maxim 的方案分为 GMSL、 GMSL2以及GMSL3。GMSL2 跟 GMSL(一代)是兼容的ÿ…...

bat命令 批处理 脚本 windows DOS
常见命令解释 命令示例: 文件1.bat echo offstart notepad.exe timeout /t 5 /nobreak start notepad.exe pause echo 当前时间【%time%】 timeout /t 5 /nobreak echo 延时时间【%time%】 pause echo off 执行bat文件的时候,cmd黑框里不显示批处理…...

【云计算】阿里云、腾讯云、华为云RocketMQ、Kafka、RabbitMq消息队列对比
目录 一、云平台中间件关键信息对比 1、RocketMQ 2、Kafka 3、RabbitMQ 二、中间件详细信息 1、阿里云MQ (一)消息队列RocketMQ (二)消息队列Kafka (三)消息队列RabbitMQ 2、腾讯云MQ (一)消息队列RocketMQ (二)消息队列CKafka (三)消息队列RabbitMQ 3、华为云MQ…...

【JavaScript脚本宇宙】玩转数据存储:深入剖析提升 Web 应用程序性能的六大利器
从本地到云端:全面解析满足各种需求的高性能 JavaScript 数据库库 前言 本文将介绍几个流行的JavaScript数据库库,包括localForage、Dexie.js、PouchDB、LokiJS和NeDB。每个库都有自己的特点和适用场景。通过比较它们的功能和使用方式,可以…...
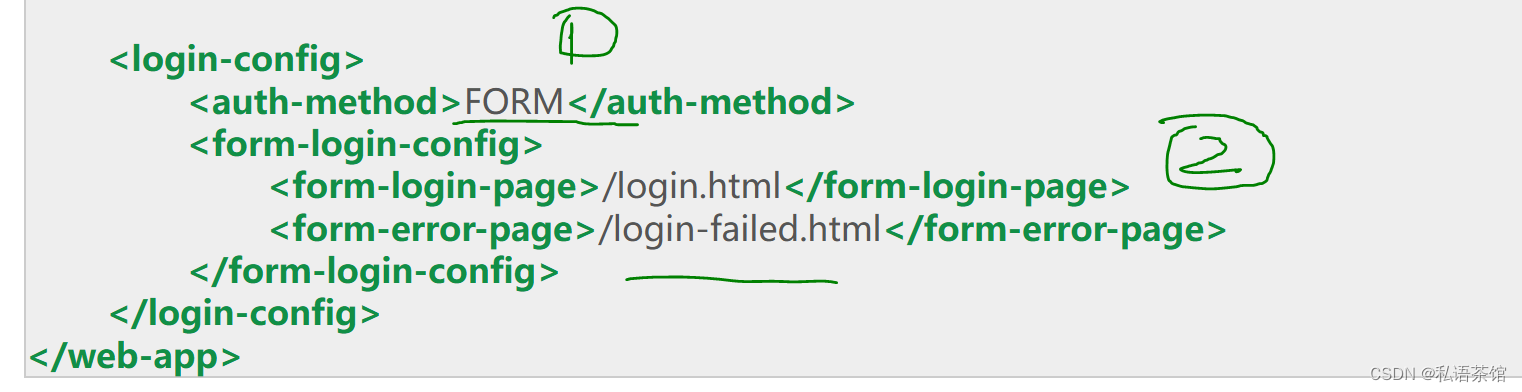
Web应用和Tomcat的集成鉴权2-Form Authentication
作者:私语茶馆 1.相关章节 1) Web应用和Tomcat的集成鉴权1-BasicAuthentication-CSDN博客 2) Web应用和Tomcat的集成鉴权2-Form Authentication-CSDN博客 集成鉴权+定制化登录 2.前言 上章讲述了Tomcat的Basic Authentication鉴权模式,可以让Web应用和Tomcat的鉴权集成起来…...

async、await 官宣:JavaScript 中的异步编程新纪元
【作者主页】:小鱼神1024 【擅长领域】:JS逆向、小程序逆向、AST还原、验证码突防、Python开发、浏览器插件开发、React前端开发、NestJS后端开发等等 async/await 是 ECMAScript 2017 标准中引入的一种用于处理异步操作的语法糖。它基于 Promise 和 Gen…...

日元跌破160大关,日本当局何时干预?
KlipC报道:6月26日,日元又跌了,美元兑日元跌破160的整关口,超过了4月日本官员在市场上干预的水平,创1986年来新低。美联储降息的可能性降低,市场预计日元有可能延续当前的弱势。 KlipC分析师David表示&…...
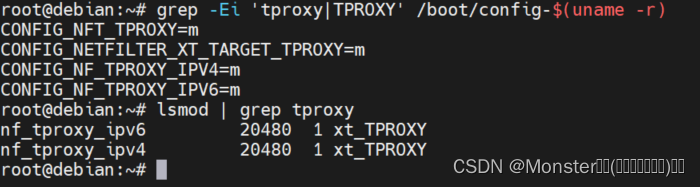
iptables(12)实际应用举例:策略路由、iptables转发、TPROXY
简介 前面的文章中我们已经介绍过iptables的基本原理,表、链的基本操作,匹配条件、扩展模块、自定义链以及网络防火墙、NAT等基本配置及原理。 这篇文章将以实际应用出发,列举一个iptables的综合配置使用案例,将我们前面所涉及到的功能集合起来,形成一个完整的配置范例。…...
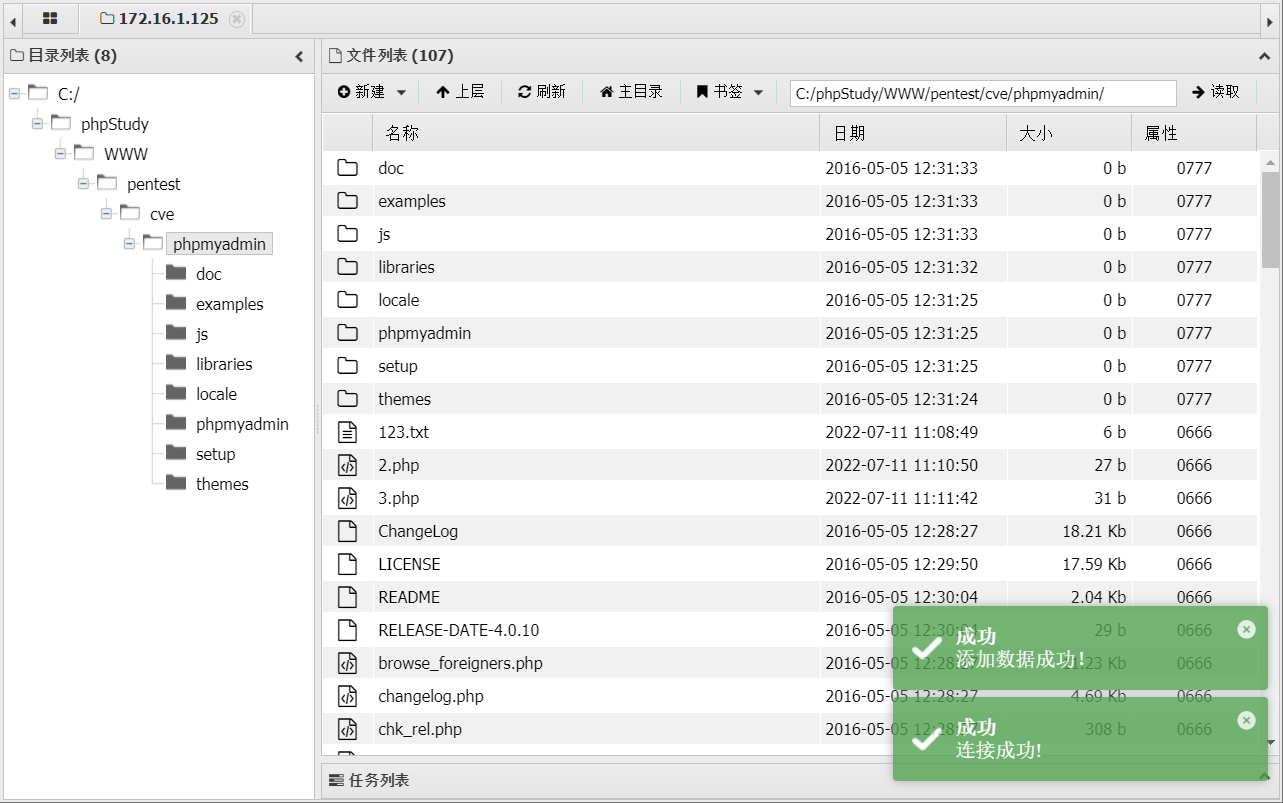
phpMyAdmin 4.0.10 文件包含 -> getshell
phpMyAdmin 4.0.10 文件包含 -> getshell 前言:这里这个漏洞相对来说审计起来不是特别难,但是对于初学者还是有点挑战性的,从zkaq web课过来的小伙伴想挑战一下自己代码审计能力的话,可以直接跳到最后下载源码,聂风…...

Spring Boot中如何集成ElasticSearch进行全文搜索
Spring Boot中如何集成ElasticSearch进行全文搜索 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将探讨如何在Spring Boot应用中集成Elas…...
HistoQC|病理切片的质量控制工具
小罗碎碎念 这期推文介绍的内容,我相信研究病理组学的人,一定都非常熟悉——HistoQC——病理切片的质量控制。 之前写过Hover Net系列的推文,反响还可以,但是Hover Net是用于细胞核检测和分类的,直接从这里开始还不够系…...

C/C++ - 编码规范(USNA版)
[IC210] Resources/C Programming Guide and Tips 所有提交的评分作业(作业、项目、实验、考试)都必须使用本风格指南。本指南的目的不是限制你的编程,而是为你的程序建立统一的风格格式。 * 这将有助于你调试和维护程序。 * 有助于他人&am…...

leetcode刷MySQL记录——sum/count里加条件判断、avg求满足条件记录数占比
leetcode题目:1934. 确认率 在刷leetcode的MySQL题中,从题目的题解知道了count和avg聚合函数的另外用法,在此记录。 count() 里加条件判断 count函数用于统计在符合搜索条件的记录中,指定的表达式expr不为NULL的行数有多少&…...

PHP的SHA256WithRSA签名和Curl POST请求函数
getCustomerEncryptionKey - 获取加密秘钥 /** * 获取加密秘钥 * param array $params * return string */ public function getCustomerEncryptionKey(array $params): string { //1.ASCII码(字典序-升序)排序…...
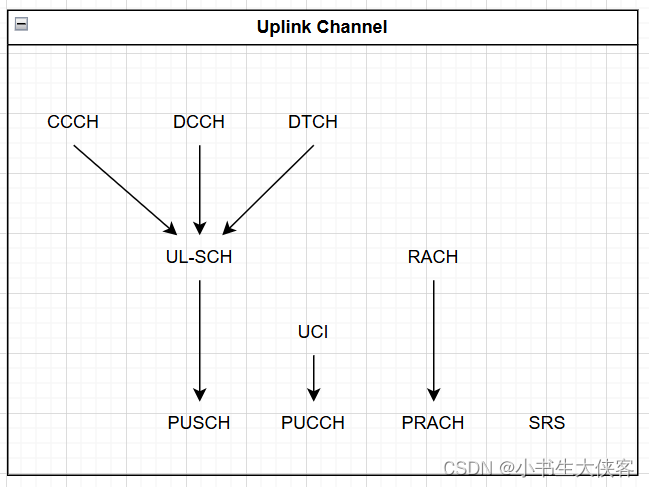
5G RAN
两个entity:NodeB、UE entity之间传输数据的东东 entity内部的流水线岗位:L3/L2/L1 岗位之间是消息交互/信令交互...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
