当前位置： 首页 > news >正文

qt for android 使用打包sqlite数据库文件方法

news 2025/9/13 18:10:50

1.在使用sqlite数据库时，先将数据库文件打包，放置在assets中如下图:

将文件放置下android中的assets下的所有文件都会打包在APK中，可以用7zip查看apk文件

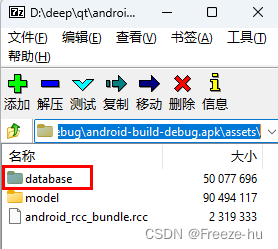
2.在qt代码读取数据文件，注意在assets下的文件都是Read-Only，需要将文件拷贝到别的路径并设置可读写权限，这样才可以操作数据库

QFile dbFile("assets:/database/doctors.sqlite");if (dbFile.exists()){qDebug()<<"the doctos.sqlite exist";QString dbPath = AppDir() +"/doctors.sqlite";//AppDir()为可以自己设定的路径 ，本程序路径是 /data/user/0/org.qtproject.example/files/doctors.sqlitedbFile.copy(dbPath);QFile::setPermissions(dbPath,QFile::WriteOwner | QFile::ReadOwner);}

3.可以读写数据库文件了 

总结:这里主要介绍数据库文件如何APK打包，并且需要将此数据库文件拷贝到别的路径下设置读写权限，操作sqlite数据的代码不做介绍了。

相关文章：

qt for android 使用打包sqlite数据库文件方法

1.在使用sqlite数据库时&#xff0c;先将数据库文件打包&#xff0c;放置在assets中如下图: 将文件放置下android中的assets下的所有文件都会打包在APK中&#xff0c;可以用7zip查看apk文件 2.在qt代码读取数据文件&#xff0c;注意在assets下的文件都是Read-Only&#xff0c;需…...

编程日记 2024/6/27 20:10:37

MYBATIS大于等于、小于等于的写法

mybatis使用的是xml格式的文件。使用>和<号的时候&#xff0c;会存在与xml的标签的规范冲突。需要写成如下形式&#xff0c;否则会报错。 第一种写法 原符号 替换符号 < < < <> > > >& &amp; &…...

编程日记 2024/6/27 20:09:36

基于堆叠长短期记忆网络 Stacked LSTM 预测A股股票价格走势

前言 系列专栏:【深度学习&#xff1a;算法项目实战】✨︎ 涉及医疗健康、财经金融、商业零售、食品饮料、运动健身、交通运输、环境科学、社交媒体以及文本和图像处理等诸多领域&#xff0c;讨论了各种复杂的深度神经网络思想&#xff0c;如卷积神经网络、循环神经网络、生成对…...

编程日记 2024/6/27 20:08:35

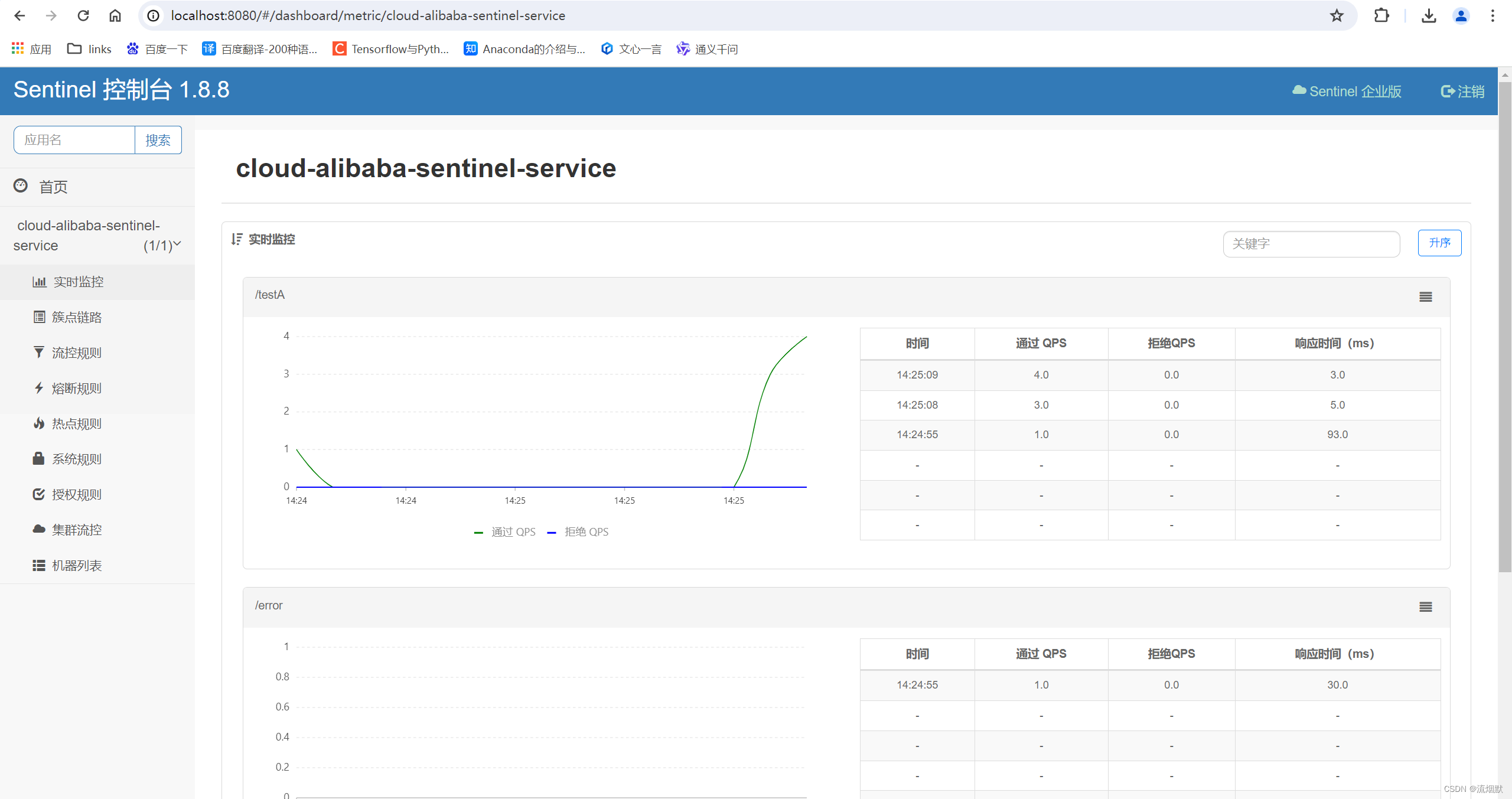
SpringCloud Alibaba Sentinel基础入门与安装

GitHub地址&#xff1a;https://github.com/alibaba/Sentinel 中文文档&#xff1a;https://sentinelguard.io/zh-cn/docs/introduction.html 下载地址&#xff1a;https://github.com/alibaba/Sentinel/releases Spring Cloud Alibaba 官方说明文档&#xff1a;Spring Clou…...

编程日记 2024/6/27 20:07:34

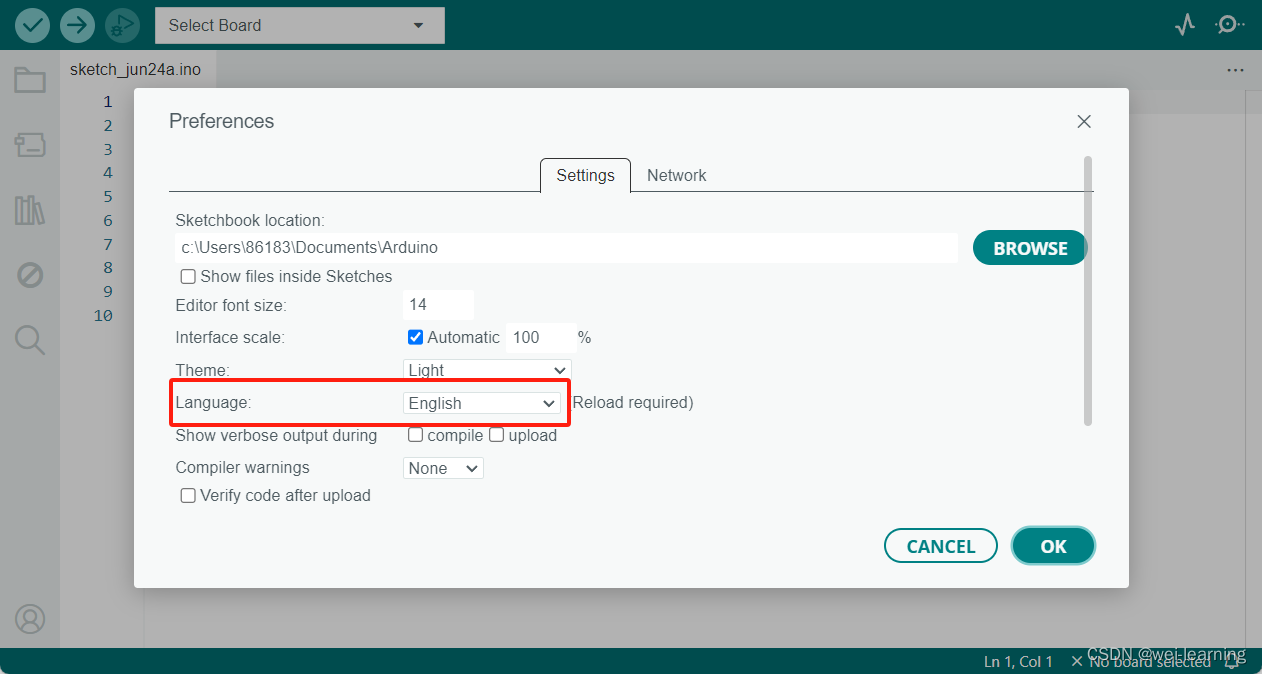
Arduino IDE下载、安装和配置

文章开始先把我自己网盘里的安装包分享给大家&#xff0c;链接&#xff1a;https://pan.baidu.com/s/1cb2_3m0LnuSKLnWP_YoWPw?pwdwwww 提取码&#xff1a;wwww 里面一个是Arduino IDE的安装包&#xff0c;另一个是即将发布的版本。 第一个安装包打开直接按照我的步骤安装就…...

编程日记 2024/6/27 20:06:33

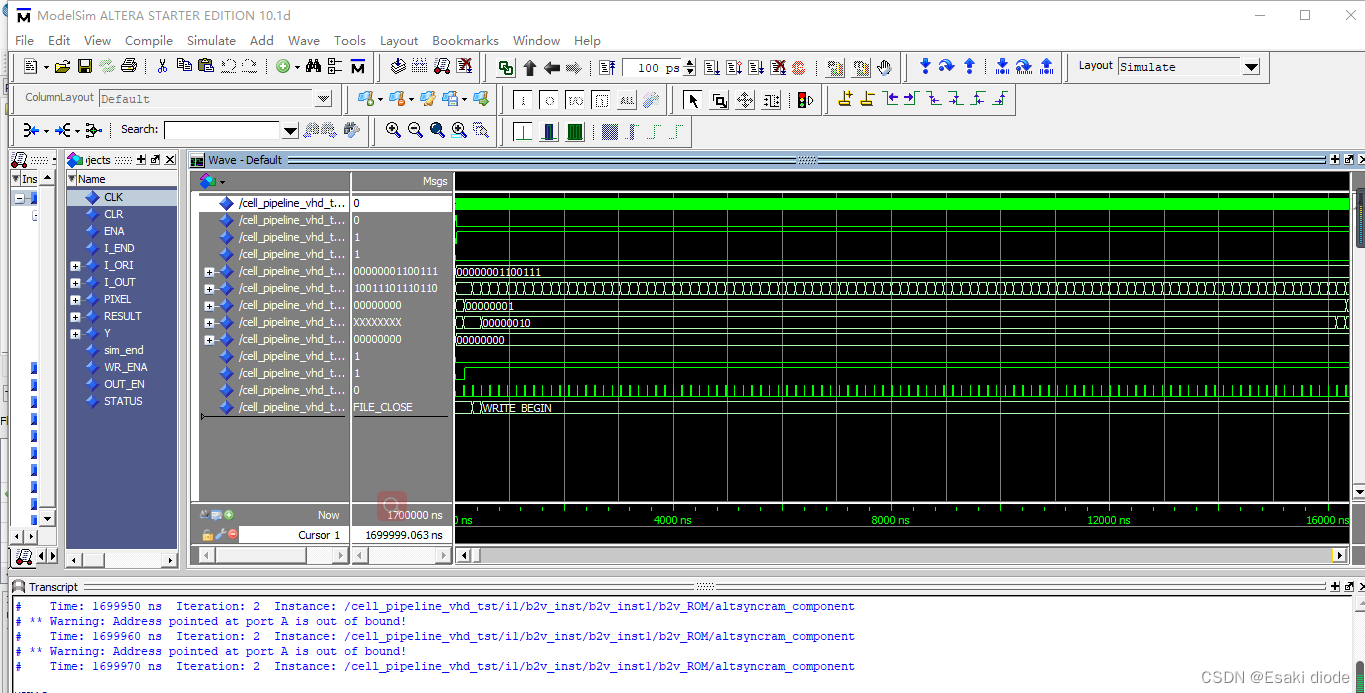
SOBEL图像边缘检测器的设计

本项目使用FPGA设计出SOBEL图像边缘检测器&#xff0c;通过分析项目在使用过程中的工作原理和相关软硬件设计进行分析详细介绍SOBEL图像边缘检测器的设计。 资料获取可联系wechat 号&#xff1a;comprehensivable 边缘可定义为图像中灰度发生急剧变化的区域边界,它是图像最基本…...

编程日记 2024/6/27 20:05:32

Day35：2734. 执行字串操作后的字典序最小字符串

Leetcode 2734. 执行字串操作后的字典序最小字符串 给你一个仅由小写英文字母组成的字符串 s 。在一步操作中&#xff0c;你可以完成以下行为&#xff1a; 选择 s 的任一非空子字符串&#xff0c;可能是整个字符串&#xff0c;接着将字符串中的每一个字符替换为英文字母表中的前…...

编程日记 2024/6/27 20:04:31

【高考志愿】机械工程

目录 一、专业概述 二、学科特点 三、就业前景 四、机械工程学科排名 五、专业选择建议 高考志愿选择机械工程&#xff0c;这是一个需要深思熟虑的决定&#xff0c;因为它不仅关乎未来的学习和职业发展&#xff0c;更是对自我兴趣和潜能的一次重要考量。 一、专业概述 机…...

编程日记 2024/6/27 20:03:29

ffmpeg将mp4转换为swf

文章目录 ffmpeg安装、配置java运行报错 Cannot run program "ffmpeg" ffmpeg命令mp4转为swf示例 ### ffmpeg -i input.mkv -b:v 600 -c:v libx264 -vf scale1920:1080 -crf 10 -ar 48000 -r 24 output.swfmkv转为swf示例 其他文档命令参数简介 需要将mp4转换为swf&a…...

编程日记 2024/6/27 20:02:28

论文学习 --- RL Regret-based Defense in Adversarial Reinforcement Learning

前言 个人拙见，如果我的理解有问题欢迎讨论 (●′ω`●) 原文链接：https://www.ifaamas.org/Proceedings/aamas2024/pdfs/p2633.pdf 研究背景 深度强化学习（Deep Reinforcement Learning, DRL）在复杂和安全关键任务中取得了显著成果，例如自动驾驶。然而，DRL策略容易受…...

编程日记 2024/6/27 20:01:27

【Linux小命令】一文讲清ldd命令及使用场景

一文讲清ldd命令及使用场景 前言下面进入正题&#xff1a;ldd命令 前言 博主今天ubuntu编译go项目出来的一个可执行文件&#xff0c;放centos运行发现居然依赖于XXlib库。然后我一下就想到两个系统库版本不一致&#xff0c;重编。换系统&#xff0c;导项目&#xff0c;配环境……...

编程日记 2024/6/27 20:00:26

自费5K,测评安德迈、小米、希喂三款宠物空气净化器谁才是高性价比之王

最近&#xff0c;家里的猫咪掉毛严重&#xff0c;简直成了一个活生生的蒲公英&#xff0c;家中、空气中各处都弥漫着猫浮毛甚至所有衣物都覆盖着一层厚厚的猫毛。令人难以置信的是&#xff0c;有时我甚至在抠出的眼屎中都能发现夹杂着几根猫毛。真的超级困扰了。但其实最空气中…...

编程日记 2024/6/27 19:59:24

1373. 二叉搜索子树的最大键值和

Problem: 1373. 二叉搜索子树的最大键值和 文章目录 思路解题方法复杂度Code 思路 解决这个问题的关键在于采用深度优先搜索&#xff08;DFS&#xff09;策略&#xff0c;并结合树形动态规划的思想。我们需要设计一个递归函数&#xff0c;它不仅能够遍历整棵树&#xff0c;还能…...

编程日记 2024/6/27 19:58:23

基于java + Springboot 的二手物品交易平台实现

目录 &#x1f4da; 前言 &#x1f4d1;摘要 &#x1f4d1;系统架构 &#x1f4da; 数据库设计 &#x1f4da; 系统功能的具体实现 &#x1f4ac; 登录模块 首页模块 二手商品轮播图添加 &#x1f4ac; 后台功能模块 二手商品商品列表 添加二手商品商品 添加购物车 &a…...

编程日记 2024/6/27 19:57:22

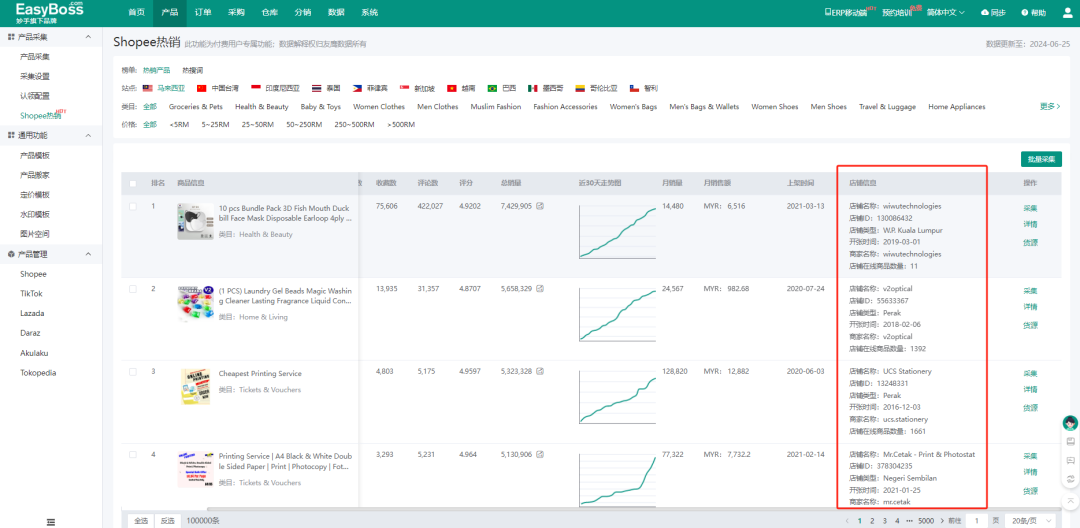
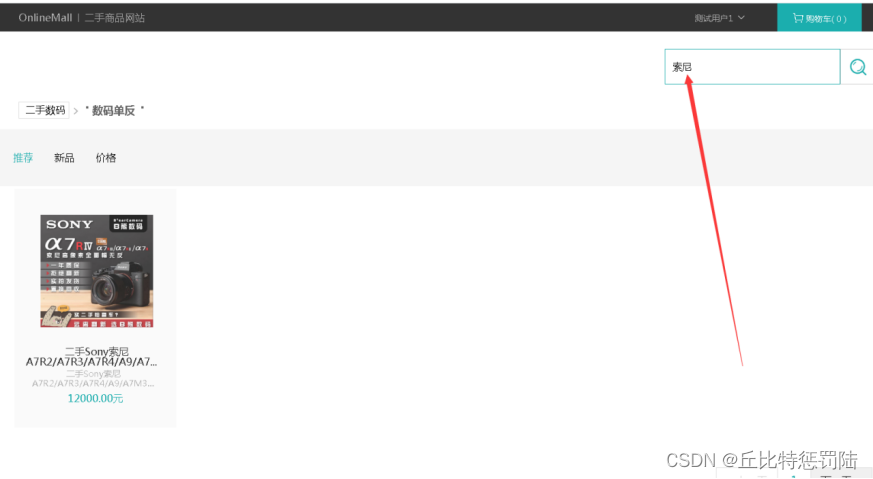
Shopee本土店选品有什么技巧？EasyBoss ERP为你整理了6个高效选品的方法！

电商圈有句话叫&#xff1a;七分靠选品&#xff0c;三分靠运营&#xff0c;选品对了&#xff0c;事半功倍&#xff0c;选品错了&#xff0c;功亏一篑&#xff01; 很多卖家都会为选品发愁&#xff0c;特别对于Shopee本土店卖家来说&#xff0c;要囤货到海外仓&#xff0c;如果…...

编程日记 2024/6/27 19:56:21

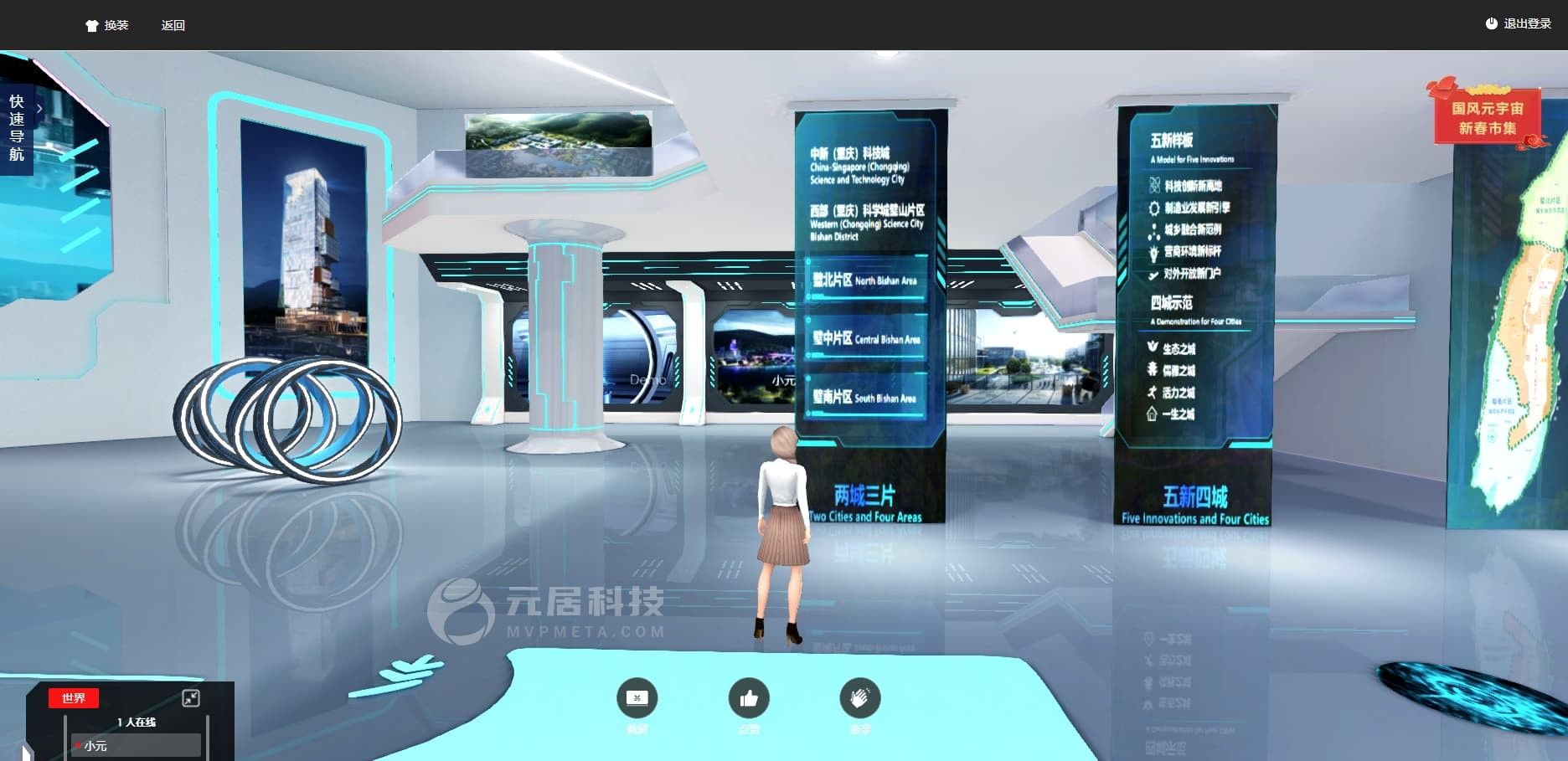
3D在线展览馆的独特魅力，技术如何重塑展览业的未来？

在数字化和虚拟现实技术迅猛发展的今天&#xff0c;3D在线展览馆已经成为一种颇具前景的创新形式。搭建3D在线展览馆不仅能够突破传统展览的时空限制&#xff0c;还能为参观者提供身临其境的体验&#xff0c;极大地提升展示效果和用户互动。 一、3D在线展览馆的意义 1、突破时空…...

编程日记 2024/6/27 19:53:19

基于SpringBoot的藏区特产销售平台

你好呀&#xff0c;我是计算机学姐码农小野&#xff01;如果有相关需求&#xff0c;可以私信联系我。 开发语言&#xff1a; Java 数据库&#xff1a; MySQL 技术&#xff1a; SpringBoot框架 工具&#xff1a; MyEclipse 系统展示 首页 个人中心 特产信息管理 订单管…...

编程日记 2024/6/27 19:52:18

hudi系列-schema evolution(一)

hudi+flink在非schema on read模式下也表现出了支持一部分的schema evolution功能，本篇中测试一下在非schema on read模式下，发生各种列变更情况时数据写入与读取情况。 flink 1.14.5hudi 0.13.1mor表思路： 选择mor表是因为它的数据文件有avro和parquet两种格式，能覆盖得更…...

编程日记 2024/6/27 19:51:17

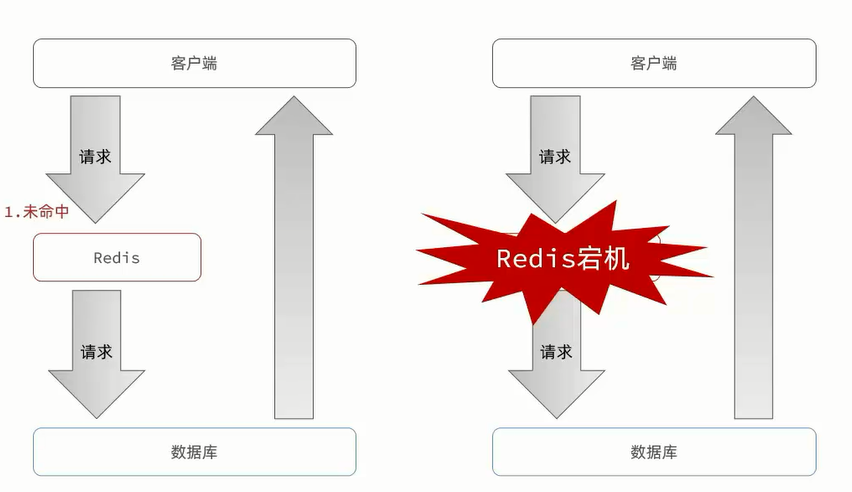
Redis-实战篇-缓存雪崩

文章目录 1、缓存雪崩2、解决方案&#xff1a; 1、缓存雪崩 缓存雪崩是指在同一时段大量的缓存key同时失效或者Redis服务宕机&#xff0c;导致大量请求到达数据库&#xff0c;带来巨大压力。 2、解决方案&#xff1a; 给不同的key的TTL添加随机值利用Redis集群提高服务的可用性…...

编程日记 2024/6/27 19:47:13

线性代数|机器学习-P18快速下降奇异值

文章目录 1. 为什么要低秩矩阵1.1 矩阵A的秩定义1.2 矩阵压缩PCA 2. 低秩矩阵图像处理3. 秩的相关性质3.1 秩的公差轴表示3.2 Eckart-Young 定理 4. 低秩矩阵4.1 低秩矩阵描述4.2 函数低秩矩阵形式4.3通项小结4.4 函数采样拟合 5. 西尔维斯特方程5.1 希尔伯特矩阵举例5.2 范德蒙…...

编程日记 2024/6/27 19:44:11

【Linux】C语言执行shell指令

在C语言中执行Shell指令 在C语言中&#xff0c;有几种方法可以执行Shell指令&#xff1a; 1. 使用system()函数 这是最简单的方法&#xff0c;包含在stdlib.h头文件中&#xff1a; #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

编程新知 2025/9/9 5:40:10

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2025/9/12 14:19:17

企业如何增强终端安全？

在数字化转型加速的今天&#xff0c;企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机&#xff0c;到工厂里的物联网设备、智能传感器&#xff0c;这些终端构成了企业与外部世界连接的 “神经末梢”。然而&#xff0c;随着远程办公的常态化和设备接入的爆炸式…...

编程新知 2025/9/9 10:11:26

Linux离线（zip方式）安装docker

目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1&#xff1a;修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本&#xff1a;CentOS 7 64位 内核版本&#xff1a;3.10.0 相关命令&#xff1a; uname -rcat /etc/os-rele…...

编程新知 2025/6/16 16:58:04

Go 语言并发编程基础：无缓冲与有缓冲通道

在上一章节中&#xff0c;我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道&#xff0c;它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好&#xff0…...

编程新知 2025/9/13 17:45:05

Oracle11g安装包

Oracle 11g安装包 适用于windows系统&#xff0c;64位 下载路径 oracle 11g 安装包...

编程新知 2025/9/13 16:14:04

第一篇：Liunx环境下搭建PaddlePaddle 3.0基础环境（Liunx Centos8.5安装Python3.10+pip3.10）

第一篇&#xff1a;Liunx环境下搭建PaddlePaddle 3.0基础环境&#xff08;Liunx Centos8.5安装Python3.10pip3.10&#xff09; 一&#xff1a;前言二&#xff1a;安装编译依赖二&#xff1a;安装Python3.10三&#xff1a;安装PIP3.10四&#xff1a;安装Paddlepaddle基础框架4.1…...

编程新知 2025/9/9 10:07:51

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能

指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

编程新知 2025/8/11 18:29:12

yaml读取写入常见错误 (‘cannot represent an object‘, 117)

错误一&#xff1a;yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因&#xff0c;后面把yaml.safe_dump直接替换成yaml.dump&#xff0c;确实能保存&#xff0c;但出现乱码&#xff1a; 放弃yaml.dump&#xff0c;又切…...

编程新知 2025/9/13 11:14:21

【若依】框架项目部署笔记

参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作&#xff1a; 压缩包下载&#xff1a;http://download.redis.io/releases 1. 上传压缩包&#xff0c;并进入压缩包所在目录&#xff0c;解压到目标…...

编程新知 2025/9/13 17:34:31