当前位置： 首页 > news >正文

CAN-bus总线在冷链运输中的应用

news 2026/2/8 22:35:24

CAN-bus总线在冷链运输中的应用

如图1所示，疫苗冷链是指为保证疫苗从疫苗生产企业到接种单位运转过程中的质量而装备的存储、运输冷藏设施、设备。由于疫苗对温度敏感，从疫苗制造的部门到疫苗使用的现场之间的每一个环节，都可能因温度过高而失效。在储运过程中，一旦温度超过2℃~8℃，疫苗就要被销毁。

图1 冷链运输示意图（图片来源于网络）

为此，疫苗冷链运输过程中确保温度的稳定是重中之重。冷链运输集装箱和配送车中都配有冷藏系统。如图2所示，为了保证通讯的实时可靠，其中冷藏机组和整车控制器主要以CAN-bus总线通信的方式。市面上也存在各种针对冷链物流的CAN总线传感器。

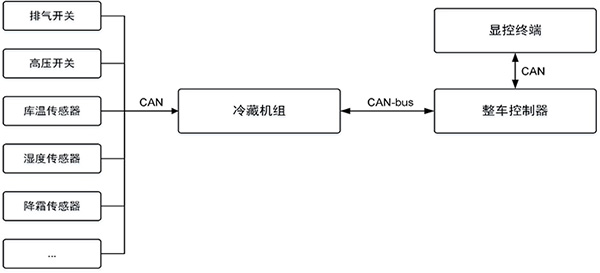
图 2冷链运输冷藏系统示意图

ZWS-CAN智慧云赋能“冷链运输”行业

物资运输过程中，如何远程实时的监控冷链运输车中温度的变化，保证产品不失效呢？上图2所示，冷藏机组内部及外部通信，依赖于CAN总线的方式。那么，只需要通过CAN-bus总线实时将温度的报文上传到后台，便可以实时的监控车辆温度变化情况。致远电子多年致力于CAN-bus产品的开发，积累的大量的经验，对此提出来可靠的方案。

  • <

相关文章：

CAN-bus总线在冷链运输中的应用

CAN-bus总线在冷链运输中的应用 如图1所示，疫苗冷链是指为保证疫苗从疫苗生产企业到接种单位运转过程中的质量而装备的存储、运输冷藏设施、设备。由于疫苗对温度敏感，从疫苗制造的部门到疫苗使用的现场之间的每一个环节，都可能因温度过高而失效。在储运过程中，一旦温度超…...

编程日记 2024/6/27 22:38:24

Vue 与 React 区别

Vue.js和React是现代Web开发中两种非常流行的前端框架&#xff0c;两者在**核心概念、组件以及生态系统扩展性**等方面存在区别。具体分析如下&#xff1a; 1. **核心概念** - **Vue**&#xff1a;Vue是一个渐进式JavaScript框架&#xff0c;它致力于视图层&#xff0c;易于上手…...

编程日记 2024/6/27 22:36:22

docker+[nginx] 部署nacos2.x 集群

docker+[nginx] 部署nacos2.x 集群 由于机器有限，本文搭建伪集群 准备： nacos1 ：192.168.50.9:8848 nacos2：192.168.50.9:8858 nacos3：192.168.50.9:8868 mysql nginx 【可选，见文末】 创建容器共享网络 便于直接使用容器名连接mysql，如果不创建，连接mysql直接使用i…...

编程日记 2024/6/27 22:35:21

Linux学习第54天：Linux WIFI 驱动：蓝星互联

Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 数字化、现代化的今天&#xff0c;随处的WIFI给与了大众极大的方便&#xff0c;也感受到了科技的力量。万物互联、无线互联越来越成为一个不可逆转的趋势。现在比较火…...

编程日记 2024/6/27 22:34:19

芯片后端之 PT 使用 report_timing 产生报告如何阅读

今天&#xff0c;就PT常用的命令&#xff0c;做一个介绍&#xff0c;希望对大家以后的工作&#xff0c;起到帮助作用。 在PrimeTime中&#xff0c;使用report_timing -delay max命令生成此报告。switch -delay max表示定时报告用于设置(这是默认值)。 首先&#xff0c;我们整…...

编程日记 2024/6/27 22:32:17

基于elastic stack搭建的ELK系统资源占用预估

1、ES 1.1 内存&#xff1a;ES非常消耗内存&#xff0c;不是JVM用到的内存,而是机器的物理内存,ES在运行期间对JVM Heap(堆内存)的需求较小 实践建议: 数据量过百万,建议单台服务器的内存至少要有16GB;数据量过亿,建议单台服务器的内存至少要有64GB 1.2 CPU&#xff1a;ES集…...

编程日记 2024/6/27 22:31:15

LiteDB - 一个单数据文件 .NET NoSQL 文档存储

LiteDB 一个小巧、快速、轻量级的 NoSQL 嵌入式数据库。 Serverless NoSQL 文档存储类似于 MongoDB 的简单 API100% C# 代码，支持 .NET 3.5 / .NET 4.0 / NETStandard 1.3 / NETStandard 2.0，单 DLL (小于 300 kb)支持线程和进程安全支持文档/操作级别的 ACID支持写失败后的数…...

编程日记 2024/6/27 22:30:14

视觉理解与图片问答，学习如何使用 GPT-4o (GPT-4 Omni) 来理解图像

&#x1f349; CSDN 叶庭云&#xff1a;https://yetingyun.blog.csdn.net/ 一、引言 OpenAI 最新发布的 GPT-4 Omni 模型&#xff0c;也被称为 GPT-4o&#xff0c;是一个多模态 AI 模型&#xff0c;旨在提供更加自然和全面的人机交互体验。 GPT-4o 与 GPT-4 Turbo 都具备视觉功…...

编程日记 2024/6/27 22:29:13

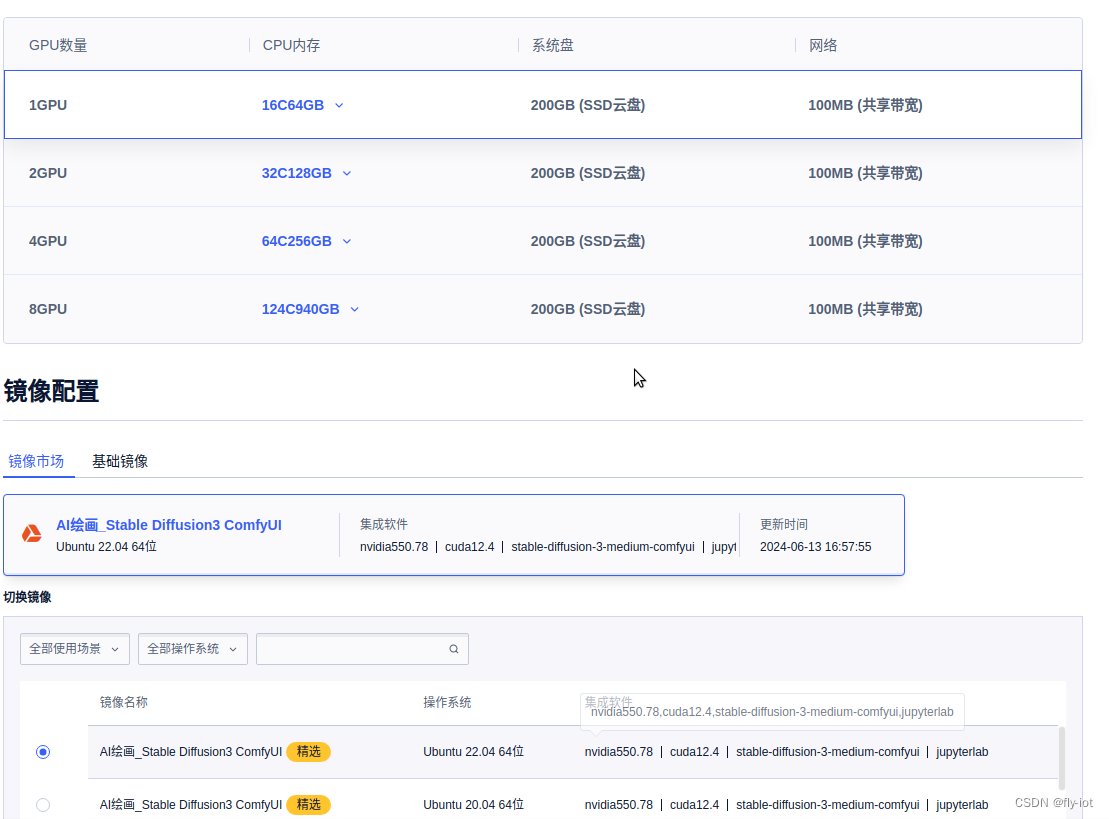
【LocalAI】（13）：LocalAI最新版本支持Stable diffusion 3，20亿参数图像更加细腻了，可以继续研究下

最新版本v2.17.1 https://github.com/mudler/LocalAI/releases Stable diffusion 3 You can use Stable diffusion 3 by installing the model in the gallery (stable-diffusion-3-medium) or by placing this YAML file in the model folder: Stable Diffusion 3 Medium 正…...

编程日记 2024/6/27 22:27:10

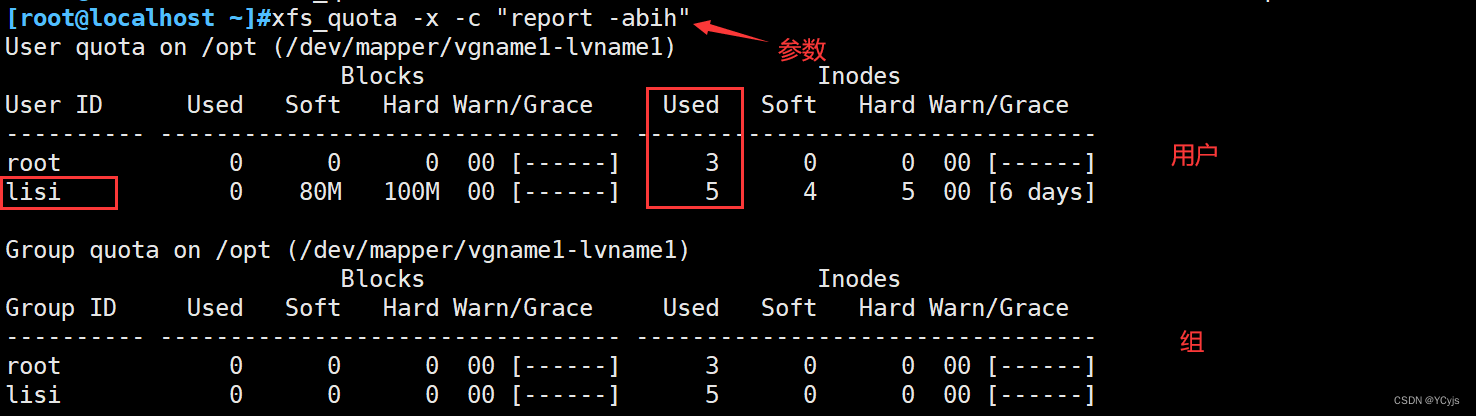
云计算【第一阶段（19）】磁盘管理与文件系统 LVM与磁盘配额（二）

目录 一、LVM概述 1.1、LVM机制的基本概念 ​编辑 1.2、LVM的管理命令 1.3、lvm存储 两种机制 1.4、lvm应用实例 二、磁盘配额概述 2.1、设置磁盘配额 2.2.1、实现磁盘限额的条件 2.2.2、linux磁盘限额的特点 2.2.3、磁盘配额管理 一、LVM概述 1.1、LVM机制的基本概…...

编程日记 2024/6/27 22:26:08

基于C++实现的EventLoop与事件驱动编程

一&#xff0c;概念介绍 事件驱动编程&#xff08;Event-Driven&#xff09;是一种编码范式&#xff0c;常被应用在图形用户界面&#xff0c;应用程序&#xff0c;服务器开发等场景。 采用事件驱动编程的代码中&#xff0c;通常要有事件循环&#xff0c;侦听事件&#xff0c;…...

编程日记 2024/6/27 22:25:07

Android高级面试_8_热修补插件化等

Android 高级面试&#xff1a;插件化和热修复相关 1、dex 和 class 文件结构 class 是 JVM 可以执行的文件类型&#xff0c;由 javac 编译生成&#xff1b;dex 是 DVM 执行的文件类型&#xff0c;由 dx 编译生成。 class 文件结构的特点&#xff1a; 是一种 8 位二进制字节…...

编程日记 2024/6/27 22:22:04

显卡GTX与RTX有什么区别？哪一个更适合玩游戏？

游戏发烧友们可能对游戏显卡并不陌生&#xff0c;它直接关系到游戏画面的流畅度、细腻程度和真实感。在众多显卡品牌中&#xff0c;英伟达的GTX和RTX系列显卡因其出色的性能而备受关注。 一、GTX与RTX的区别 架构差异 GTX系列显卡采用的是Pascal架构&#xff0c;这是英伟达在…...

编程日记 2024/6/27 22:21:03

QT自定义信号和槽函数

在QT中最重要也是必须要掌握的机制&#xff0c;就是信号与槽机制&#xff0c;在MFC上也就是类型的机制就是消息与响应函数机制 在QT中我们不仅要学会如何使用信号与槽机制&#xff0c;还要会自定义信号与槽函数&#xff0c;要自定义的原因是系统提供的信号&#xff0c;在一些情…...

编程日记 2024/6/27 22:19:00

Atcoder Beginner Contest 359

传送门 A - Count Takahashi 时间限制&#xff1a;2秒 内存限制&#xff1a;1024MB 分数&#xff1a;100分 问题描述 给定 N 个字符串。 第 i 个字符串 () 要么是 Takahashi 要么是 Aoki。 有多少个 i 使得 等于 Takahashi &#xff1f; 限制 N 是整数。每个…...

编程日记 2024/6/27 22:17:58

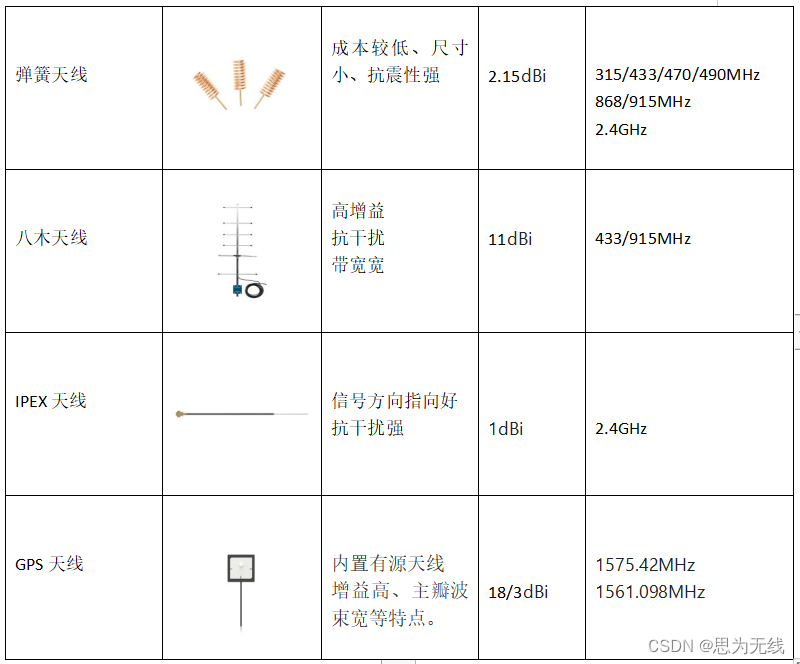
无线通讯几种常规天线类别简介

天线对于无线模块来说至关重要&#xff0c;合适的天线可以优化通信网络&#xff0c;增加其通信的范围和可靠性。天线的选型对最后的模块通信影响很大&#xff0c;不合适的天线会导致通信质量下降。针对不同的市场应用&#xff0c;天线的材质、安置方式、性能也大不一样。下面简…...

编程日记 2024/6/27 22:16:57

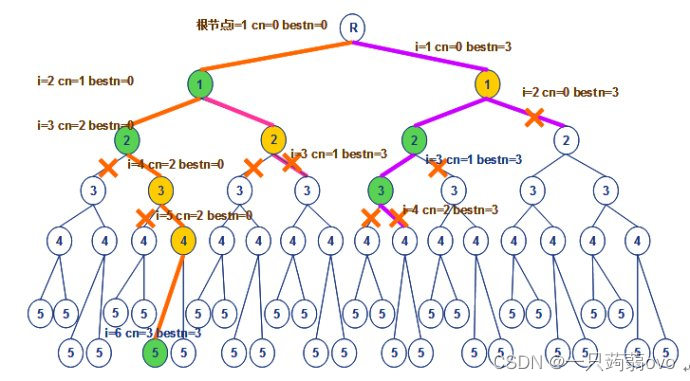
最大团问题--回溯法

一、相关定义 给定一个无向图 &#xff0c;其中 V 是图的顶点集&#xff0c;E图的边集 完全图&#xff1a;如果无向图中的任何一对顶点之间都有边&#xff0c;这种无向图称为完全图 完全子图&#xff1a;给定无向图 &#xff0c;如果 &#xff0c;且对应任意 且 &#xff0c;则…...

编程日记 2024/6/27 22:15:56

MBSE之简单介绍

MBSE之简单介绍 文章目录 MBSE之简单介绍1. What is MBSE&#xff1f;2. MBSE 最佳实践 1. What is MBSE&#xff1f; Model-Based Systems Engineering (MBSE), a.k.a. Model-Based Systems Development (MBSD), is a Systems Engineering process paradigm that emphasizes t…...

编程日记 2024/6/27 22:13:54

基于ODPS解析字段值为JSON的情况

最近在使用ODPS数据库&#xff0c;其中一个字段他是用JSON存储的&#xff0c;但是我是需要JSON字符串中的一个属性值就行&#xff0c;刚好ODPS中有一个函数可以用来使用! 使用案例 select GET_JSON_OBJECT({"id":1,"name":"xiaobai"},$.name);…...

编程日记 2024/6/27 22:12:52

CesiumJS【Basic】- #020 加载glb/gltf文件（Primitive方式）

文章目录 加载glb/gltf文件（Primitive方式）1 目标2 代码实现3 资源文件加载glb/gltf文件（Primitive方式） 1 目标 使用Primitive方式加载glb/gltf文件 2 代码实现 import * as Cesium from "cesium";const viewer = new Cesium.Viewer...

编程日记 2024/6/27 22:09:50

国防科技大学计算机基础课程笔记02信息编码

1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制&#xff0c;因此这个了16进制的数据既可以翻译成为这个机器码&#xff0c;也可以翻译成为这个国标码&#xff0c;所以这个时候很容易会出现这个歧义的情况&#xff1b; 因此&#xff0c;我们的这个国…...

编程新知 2026/2/8 4:37:15

C++初阶-list的底层

目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

编程新知 2026/2/8 20:42:41

前端倒计时误差!

提示：记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来？二、五大解决方案1. 动态校准法（基础版）2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

编程新知 2025/9/8 23:14:43

【机器视觉】单目测距——运动结构恢复

ps&#xff1a;图是随便找的&#xff0c;为了凑个封面 前言 在前面对光流法进行进一步改进&#xff0c;希望将2D光流推广至3D场景流时&#xff0c;发现2D转3D过程中存在尺度歧义问题&#xff0c;需要补全摄像头拍摄图像中缺失的深度信息&#xff0c;否则解空间不收敛&#xf…...

编程新知 2026/2/8 3:03:01

Psychopy音频的使用

Psychopy音频的使用 本文主要解决以下问题&#xff1a; 指定音频引擎与设备&#xff1b;播放音频文件 本文所使用的环境&#xff1a; Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

编程新知 2026/1/31 15:09:31

Ascend NPU上适配Step-Audio模型

1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统&#xff0c;支持多语言对话&#xff08;如 中文&#xff0c;英文&#xff0c;日语&#xff09;&#xff0c;语音情感&#xff08;如 开心&#xff0c;悲伤&#xff09;&#x…...

编程新知 2026/1/31 4:37:39

图表类系列各种样式PPT模版分享

图标图表系列PPT模版&#xff0c;柱状图PPT模版&#xff0c;线状图PPT模版&#xff0c;折线图PPT模版&#xff0c;饼状图PPT模版&#xff0c;雷达图PPT模版&#xff0c;树状图PPT模版 图表类系列各种样式PPT模版分享&#xff1a;图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

编程新知 2026/2/4 18:07:02

虚拟电厂发展三大趋势：市场化、技术主导、车网互联

市场化&#xff1a;从政策驱动到多元盈利 政策全面赋能 2025年4月&#xff0c;国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》&#xff0c;首次明确虚拟电厂为“独立市场主体”&#xff0c;提出硬性目标&#xff1a;2027年全国调节能力≥2000万千瓦&#xff0…...

编程新知 2025/12/20 18:09:59

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能

1. 开发环境准备 ​​安装DevEco Studio 3.1​​&#xff1a; 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK ​​项目配置​​&#xff1a; // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

编程新知 2025/12/29 15:43:26

day36-多路IO复用

一、基本概念 &#xff08;服务器多客户端模型&#xff09; 定义&#xff1a;单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用&#xff1a;应用程序通常需要处理来自多条事件流中的事件&#xff0c;比如我现在用的电脑&#xff0c;需要同时处理键盘鼠标…...

编程新知 2026/1/31 7:42:50