Atcoder Beginner Contest 359
传送门
A - Count Takahashi
时间限制:2秒 内存限制:1024MB
分数:100分
问题描述
给定 N 个字符串。
第 i 个字符串 (
) 要么是 Takahashi 要么是 Aoki。
有多少个 i 使得 等于 Takahashi ?
限制
- N 是整数。
- 每个字符串
是 Takahashi 或者 Aoki。(
)
输入格式
输出格式
输出 等于 Takahashi 的数量。
样例输入输出
样例输入1
样例输出1
和
等于 Takahashi,而
不等于 Takahashi。
因此,输出 2。
样例输入2
样例输出2
没有 等于 Takahashi。
样例输入3
样例输出3
代码
#include <bits/stdc++.h>
using namespace std;inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}int main () {int n = read(), cnt = 0;while (n--) {string s;cin >> s;if (s[0] == 'T') cnt++;}cout << cnt;return 0;
}B - Couples
时间限制:2秒 内存限制:1024MB
分数:150分
问题描述
有 2N 个人站成一排,位于第i个位置的人穿着颜色为 的衣服。这里,衣服有 N 种颜色,每种颜色正好有两个人穿。
找出满足以下条件的整数 的数量:
- 颜色为 i 的两个人之间正好有一个人。
限制
- 每个从 1 到 N 的每个整数在 A 中恰好出现两次。
- 所有输入值都是整数。
输入格式
输出格式
输出答案
样例输入输出
样例输入1
样例输出1
有两个 i 值满足条件:1 和 3。
实际上,穿着颜色为 1 的衣服的人分别在从左数第 1 和第 3 的位置,中间正好有一个人。
样例输入2
样例输出2
没有 i 值满足条件。
样例输入3
样例输出3
代码
#include <bits/stdc++.h>
using namespace std;inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}int main () {int n = read(), a[205], cnt = 0;for (int i = 1; i <= 2 * n; i++) a[i] = read();for (int i = 1; i < 2 * n; i++) {for (int j = i + 1; j <= 2 * n; j++) {if (a[i] == a[j] && j == i + 2) {cnt++;break;}}}cout << cnt;return 0;
}C - Tile Distance 2
时间限制:2秒 内存限制:1024MB
分数:350分
问题描述
坐标平面被 2 × 1 的瓷砖覆盖。瓷砖的铺设遵循以下规则:
- 对于整数对 (i, j),方块
包含在一块瓷砖中。
- 当 i + j 是偶数时,
和
包含在同一块瓷砖中。
瓷砖包括它们的边界,并且没有两块不同的瓷砖共享正面积。
在靠近原点的地方,瓷砖的铺设如下:

Takahashi 从坐标平面上的点 ( + 0.5,
+ 0.5) 开始。
他可以重复以下移动操作任意次数:
选择一个方向(上,下,左,右)和一个正整数 n。向该方向移动 n 个单位。
每次他进入一个瓷砖,他需要支付 1 的费用。
求他到达点 ( + 0.5,
+ 0.5) 所需支付的最少费用。
限制
- 所有输入都是整数。
输入格式
输出格式
输出 Takahashi 需要支付的最少费用。
样例输入输出
样例输入1
样例输出1
例如,Takahashi 可以通过以下移动支付 5 的费用:

- 向左移动 1。支付 0 的费用。
- 向上移动 1。支付 1 的费用。
- 向左移动 1。支付 0 的费用。
- 向上移动 3。支付 3 的费用。
- 向左移动 1。支付 0 的费用。
- 向上移动 1。支付 1 的费用。
无法将费用减少到 4 或更少,因此输出 5。
样例输入2
样例输出2
有些情况下不需要支付任何费用。
样例输入3
样例输出3
注意,输出的值可能会超过 32 位整数的范围。
思路
将移动分为竖直方向跟水平方向来考虑。
任何情况下,在竖直方向上的移动需要支付 。与此同时也能在水平方向上移动
个单位,所以要给
加上
。如果在此之后水平方向依旧无法到达,则需要加上
。
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main () {int a, b, c, d;cin >> a >> b >> c >> d;if (a > c) swap(a, c), swap(b, d);if ((c + d) & 1) c--;if ((a + b) % 2 == 0) a++;int ans = abs(b - d);a += ans;if (a < c) ans += (c - a + 1) / 2;cout << ans;return 0;
}E - Water Tank
时间限制:2秒 内存限制:1024MB
分数:500分
问题描述
给定一个长度为 N 的正整数序列 。
有一个长度为 N + 1 的非负整数序列 ,初始时
。
重复执行以下操作直到结束:
1. 将 的值增加 1。
2. 对于每个 ,按顺序执行以下操作:
如果 并且
,则将
的值减少 1,同时将
的值增加 1。
对于每个 ,找出在
首次成立之前执行了多少次操作。
限制
- 所有输入都是整数。
输入格式
输出格式
将对于每个 的答案输出在一行上,以空格分隔。
样例输入输出
样例输入1
样例输出1
前五次操作如下。
这里,每一行对应一次操作,最左边的列代表步骤 1,其余的代表步骤 2。
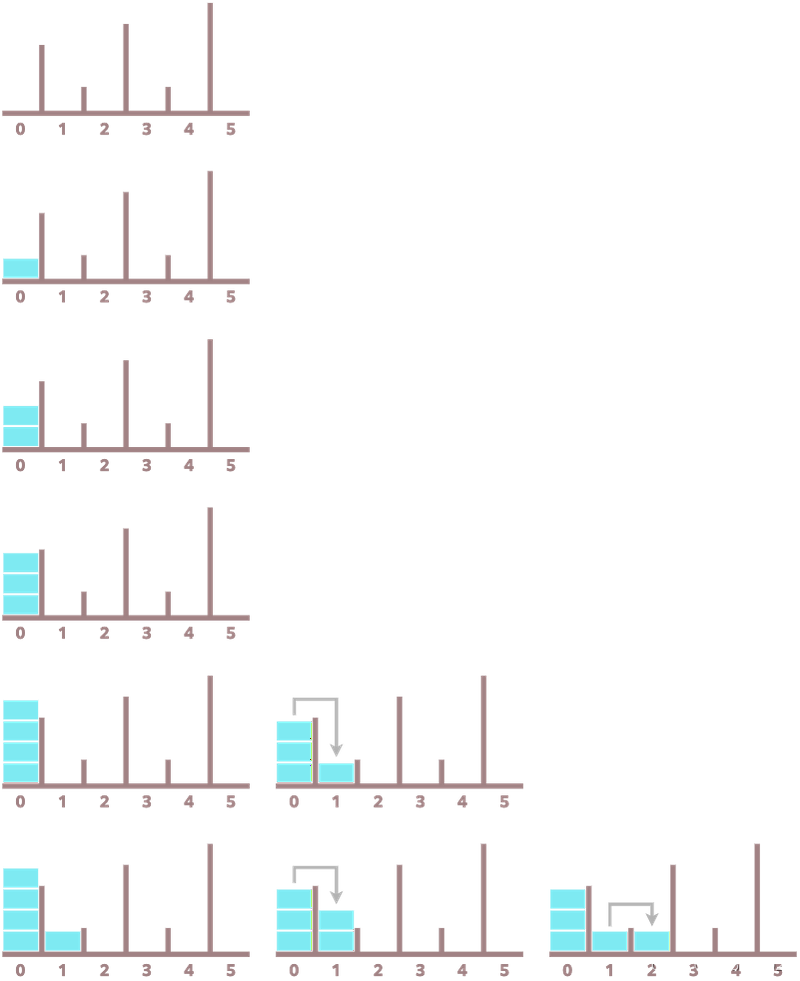
从这个图表中可以看出, 首次在第4次操作后成立,而
首次在第5次操作后成立。
类似地, 的答案分别是 13,14,26。
因此,你应该输出 4 5 13 14 26。
样例输入2
样例输出2
请注意,输出的值可能超出 32 位整数的范围。
样例输入3
样例输出3
思路
先说歪解:看样例猜答案
我们很容易能发现每一个输出第第一项都是 。当
的时候,如果
,那么
;否则
。
(至于为什么各位先别急
是因为
才能将大于
的部分转移到
上
每次操作第二步的转移,题目意思是从 上连续转移到最右边可以转移的位置上,但这个也等价于在任意
上加 1,再向右转移
- 如果
,那么在这个条件下,只需要在
上加 1,再将这个 1 转移到
上去即可(1步操作),所以
。
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int n, h[N], a[N], maxid = 1;
inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}
stack<int> s;
signed main () {n = read();for (int i = 1; i <= n; i++) h[i] = read();for (int i = 1; i <= n; i++) {while (s.size() && h[s.top()] < h[i]) s.pop();if (s.size()) a[i] = a[s.top()] + (i - s.top()) * h[i];else a[i] = i * h[i] + 1;s.push(i);}for (int i = 1; i <= n; i++) printf("%lld ", a[i]);return 0;
}F - Tree Degree Optimization
时间限制:2秒 内存限制:1024MB
分数:550分
问题描述
你有一个整数序列 。对于一棵有 N 个顶点的树 T,定义函数 f(T) 如下:
- 令
为顶点 i 在树 T 中的度数。那么
。
找出 f(T) 的最小可能值。
约束条件保证答案小于 。
限制
- 所有输入都是整数。
输入格式
输出格式
输出答案
样例输入输出
样例输入1
样例输出1
考虑一棵树 T,一条边连接顶点 1 和顶点 2,一条边连接顶点 2 和顶点 4,一条边连接顶点 4 和顶点 3。
那么,。 可以证明这是 f(T) 的最小值。
样例输入2
样例输出2
样例输入3
样例输出3
思路
由于是一棵树,所以树中总共有 N - 1 条边,那么每个节点的度的范围为 ,每个节点的度的和
。
最开始的时候,把每个节点的度初始化为 1。接着再用一个优先队列维护每一个节点的度加一后,f(T) 增加的最小值。因为 ,所以只需要把
放入优先队列,在维护一个小根堆即可。
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int n, a[N], d[N], ans = 0LL;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}
signed main () {n = read();for (int i = 1; i <= n; i++) a[i] = read();for (int i = 1; i <= n; i++) {d[i] = 1, ans += a[i];q.push({3 * a[i], i});}for (int i = 1; i <= n - 2; i++) {int x = q.top().first, y = q.top().second;q.pop();ans += a[y] * (2 * d[y] + 1);d[y]++;q.push({a[y] * (2 * d[y] + 1), y});}printf("%lld", ans);return 0;
}相关文章:
Atcoder Beginner Contest 359
传送门 A - Count Takahashi 时间限制:2秒 内存限制:1024MB 分数:100分 问题描述 给定 N 个字符串。 第 i 个字符串 () 要么是 Takahashi 要么是 Aoki。 有多少个 i 使得 等于 Takahashi ? 限制 N 是整数。每个…...
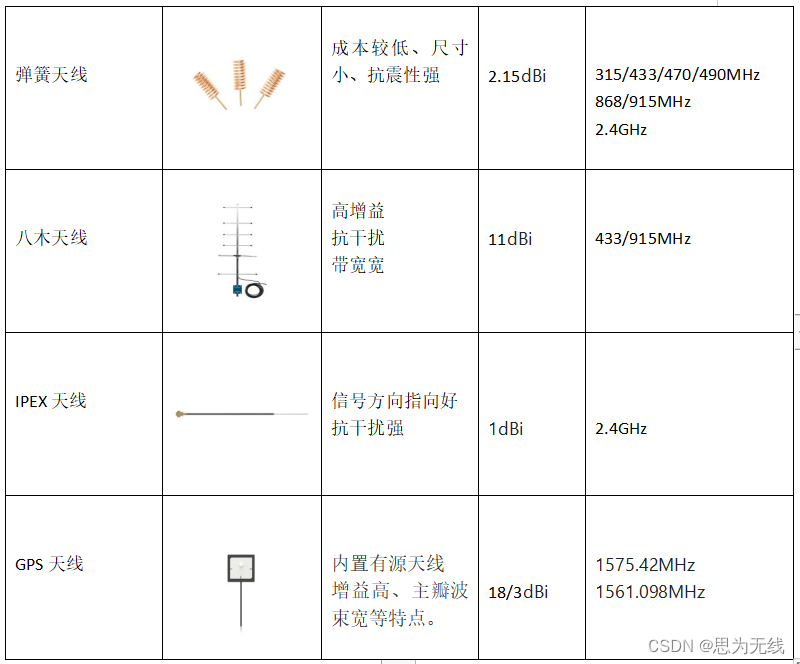
无线通讯几种常规天线类别简介
天线对于无线模块来说至关重要,合适的天线可以优化通信网络,增加其通信的范围和可靠性。天线的选型对最后的模块通信影响很大,不合适的天线会导致通信质量下降。针对不同的市场应用,天线的材质、安置方式、性能也大不一样。下面简…...
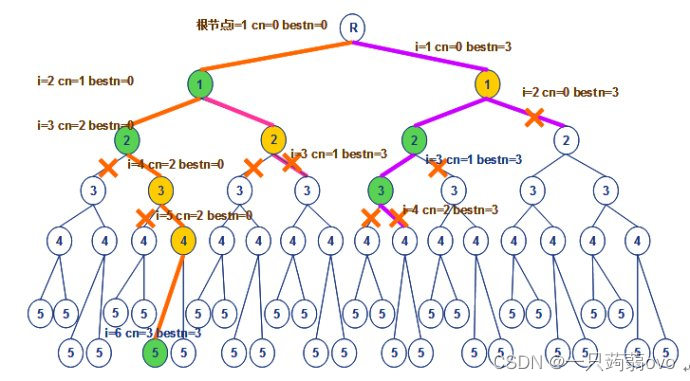
最大团问题--回溯法
一、相关定义 给定一个无向图 ,其中 V 是图的顶点集,E图的边集 完全图:如果无向图中的任何一对顶点之间都有边,这种无向图称为完全图 完全子图:给定无向图 ,如果 ,且对应任意 且 ,则…...

MBSE之简单介绍
MBSE之简单介绍 文章目录 MBSE之简单介绍1. What is MBSE?2. MBSE 最佳实践 1. What is MBSE? Model-Based Systems Engineering (MBSE), a.k.a. Model-Based Systems Development (MBSD), is a Systems Engineering process paradigm that emphasizes t…...

基于ODPS解析字段值为JSON的情况
最近在使用ODPS数据库,其中一个字段他是用JSON存储的,但是我是需要JSON字符串中的一个属性值就行,刚好ODPS中有一个函数可以用来使用! 使用案例 select GET_JSON_OBJECT({"id":1,"name":"xiaobai"},$.name);…...

CesiumJS【Basic】- #020 加载glb/gltf文件(Primitive方式)
文章目录 加载glb/gltf文件(Primitive方式)1 目标2 代码实现3 资源文件加载glb/gltf文件(Primitive方式) 1 目标 使用Primitive方式加载glb/gltf文件 2 代码实现 import * as Cesium from "cesium";const viewer = new Cesium.Viewer...

2024黑盾杯复现赛题MISC部分
一、一个logo 一张png图片,查看颜色通道即可发现flag 二、 学会Office 最好用联想自带的excel工具查看,我用WPS打开未解出题目 这里会发现有隐藏信息 隐藏信息为宏加密 。去百度了解宏加密后,发现有俩个宏,一个加密一个解密 执…...

Linux0.12内核源码解读(5)-head.s
大家好,我是呼噜噜,好久没有更新old linux了,本文接着上一篇文章图解CPU的实模式与保护模式,继续向着操作系统内核的世界前进,一起来看看heads.s as86 与GNU as 首先我们得了解一个事实,在Linux0.12内核源…...
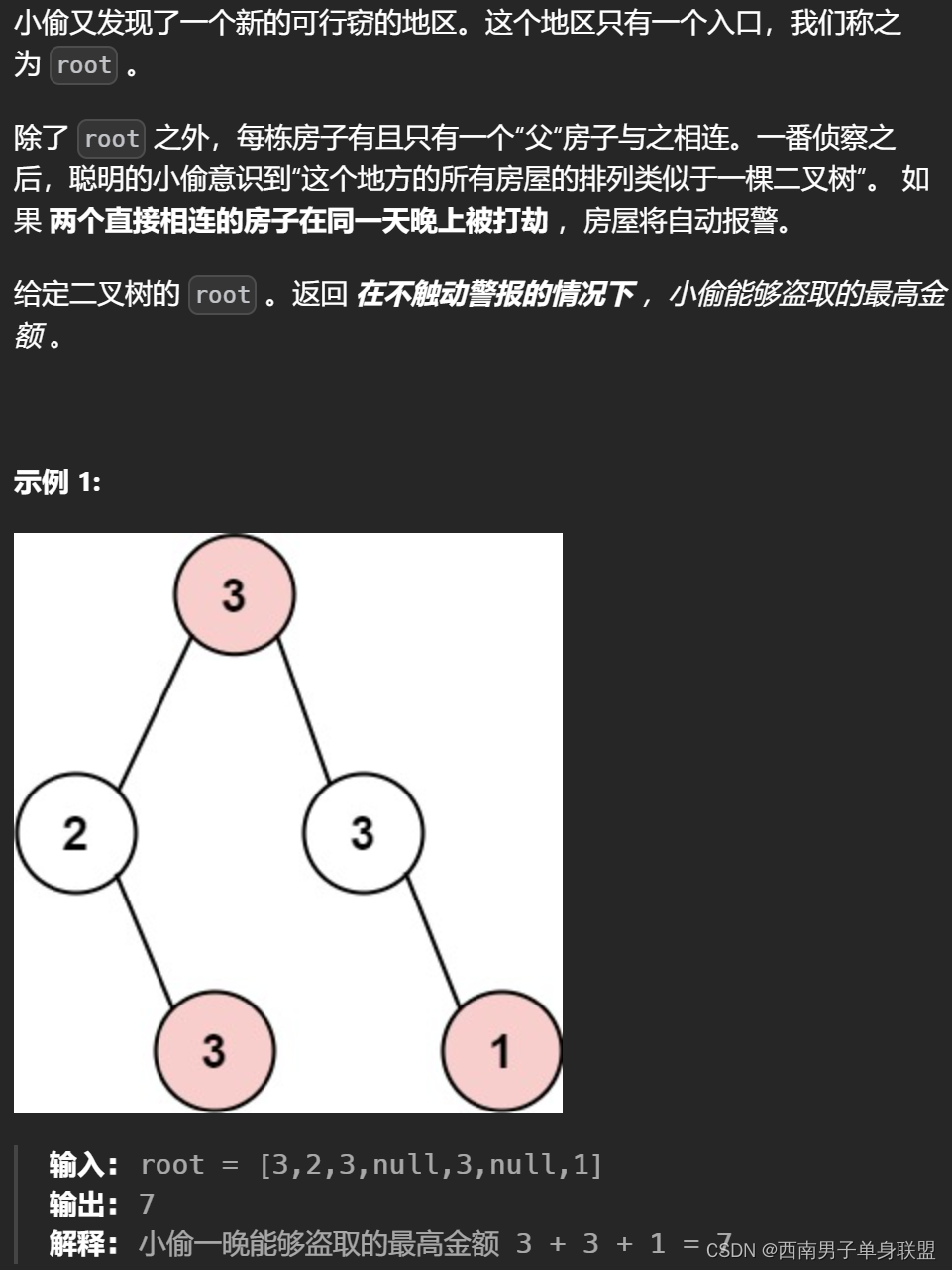
刷代码随想录有感(119):动态规划——打家劫舍III(树形dp)
题干: 代码: class Solution { public:vector<int>dp(TreeNode* cur){if(cur NULL)return vector<int>{0, 0};vector<int> left dp(cur -> left);vector<int> right dp(cur -> right);//偷int val1 cur -> val l…...

vivado CARRY_REMAP、CASCADE_HEIGHT
CARRY_REMAP opt_design-carry_remap选项可用于将单个carry*单元重新映射到LUT中 提高了布线的设计效果。使用-carry_remap选项时,仅 将单级进位链转换为LUT。CARRY_REMAP属性允许您 指定在优化过程中要转换的长度较大的进位链。 您可以使用控制任意长度的单个进位链…...
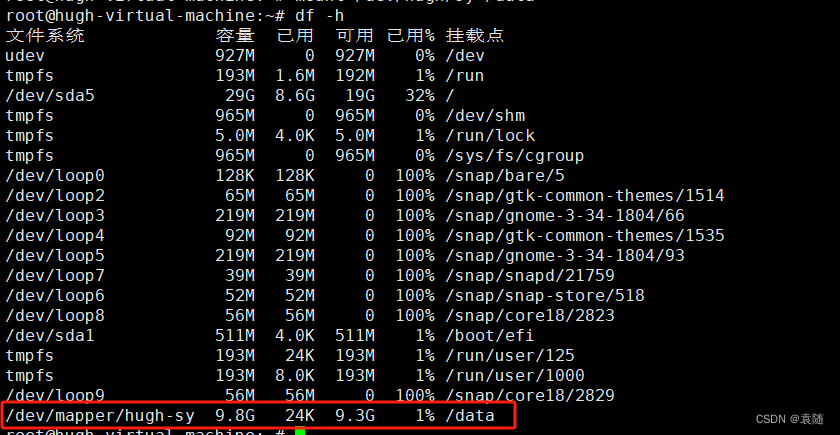
Ubuntu磁盘分区和挂载 虚拟机扩容 逻辑卷的创建和扩容保姆及教程
目录 1、VMware虚拟机Ubuntu20.04系统磁盘扩容 2、Linux的磁盘分区和挂载 3、创建逻辑卷和逻辑卷的扩容 1、VMware虚拟机Ubuntu20.04系统磁盘扩容 通过下图可以看出我们的根磁盘一共有20G的大小,现在我们把它扩容为30G 注:如果你的虚拟机有快照是无…...

【附精彩文章合辑】哈佛辍学小哥的创业经历【挑战英伟达!00 后哈佛辍学小哥研发史上最快 AI 芯片,比 H100 快 20 倍!】
前情提要 https://blog.csdn.net/weixin_42661676/article/details/140020491 哈佛辍学小哥的创业经历 一、背景与起步 这位哈佛辍学小哥,名为Chris Zhu,是一位华裔学生,他在2020年进入哈佛大学,攻读数学学士学位和计算机科学硕…...

Oracle CPU使用率过高问题处理
1.下载Process Explorer 2.打开Process Explorer,查看CPU使用情况最高的进程 3.双击该进程,查看详情 \ 4. 获取cpu使用最好的线程tid 5. 查询sql_id select sql_id from v$session where paddr in( select addr from v$process where spid in(1…...

pyqt的QWidgetList如何多选?如何按下Ctrl多选?
通过设置setSelectionMode(QAbstractItemView.MultiSelection),可以实现QWidgetList的多选。 但是上述结果不太符合我们需求。设置多选模式后,只需鼠标点击就可以选择多个条目。 我希望按下Ctrl键时才进行多选,仅鼠标单击的话,只进…...

【电路笔记】-MOSFET放大器
MOSFET放大器 文章目录 MOSFET放大器1、概述2、电路图3、电气特性3.1 ** I D = F ( V G S ) I_D=F(V_{GS}) ID=F(VGS)**特性3.2 I D = F ( V D S ) I_D=F(V_{DS}) ID=F(VDS)特性4、MOSFET放大器5、输入和输出电压6、电压增益7、总结1、概述 在前面的文章中,我们已经…...
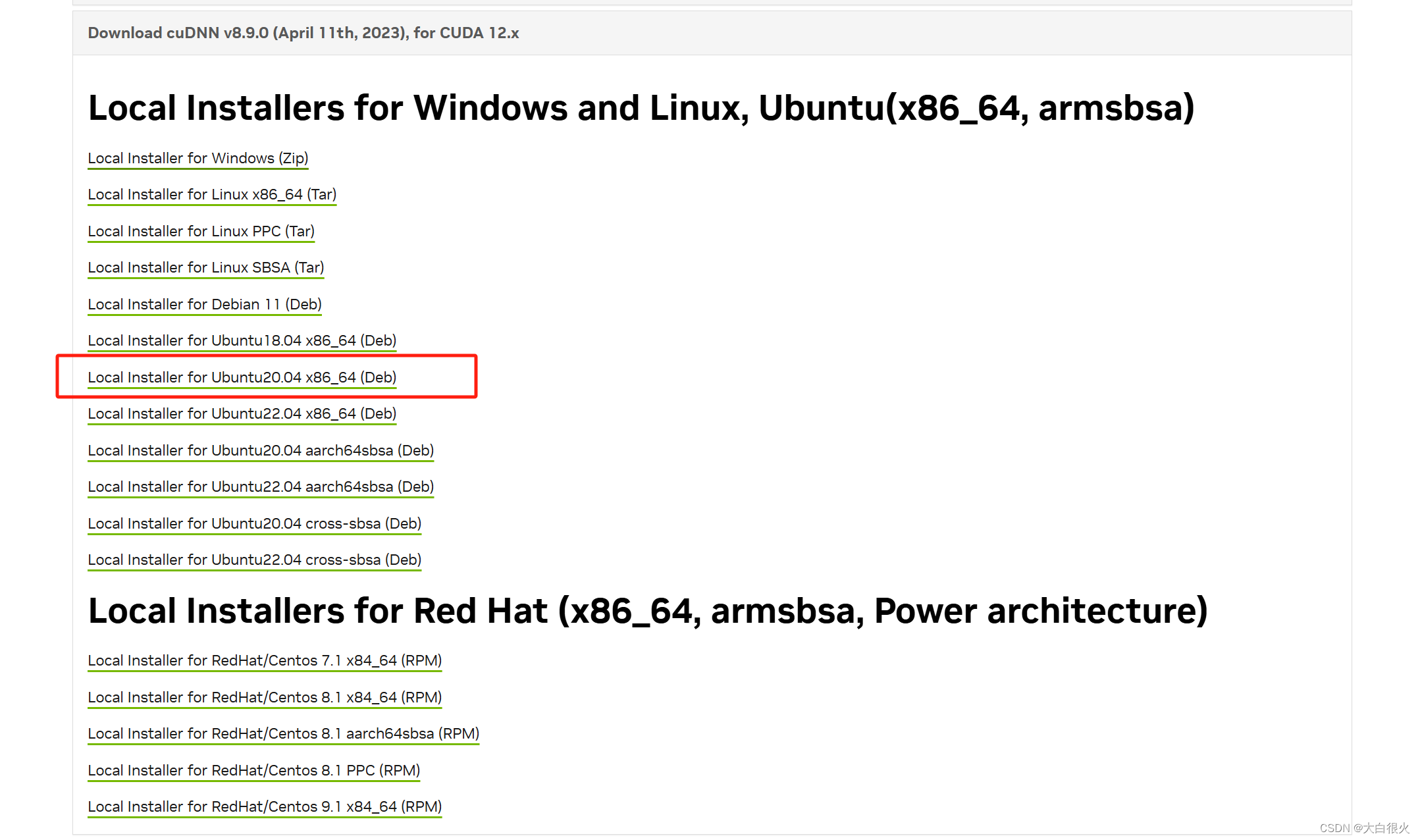
Ubuntu 20.04安装显卡驱动、CUDA、Pytorch(2024.06最新)
文章目录 一、安装显卡驱动1.1 查看显卡型号1.2 根据显卡型号选择驱动1.3 获取下载链接1.4 查看下载的显卡驱动安装文件1.5 更新软件列表和安装必要软件、依赖1.6 卸载原有驱动1.7 禁用默认驱动1.8 安装lightdm显示管理器1.9 停止显示服务器1.10 在文本界面中,禁用X…...

wpf 附加属性 RegisterAttached 内容属性
// // 摘要: // 选中时展示的元素 public static readonly DependencyProperty CheckedElementProperty DependencyProperty.RegisterAttached("CheckedElement", typeof(object), typeof(StatusSwitchElement), new PropertyMetadata((object)null…...
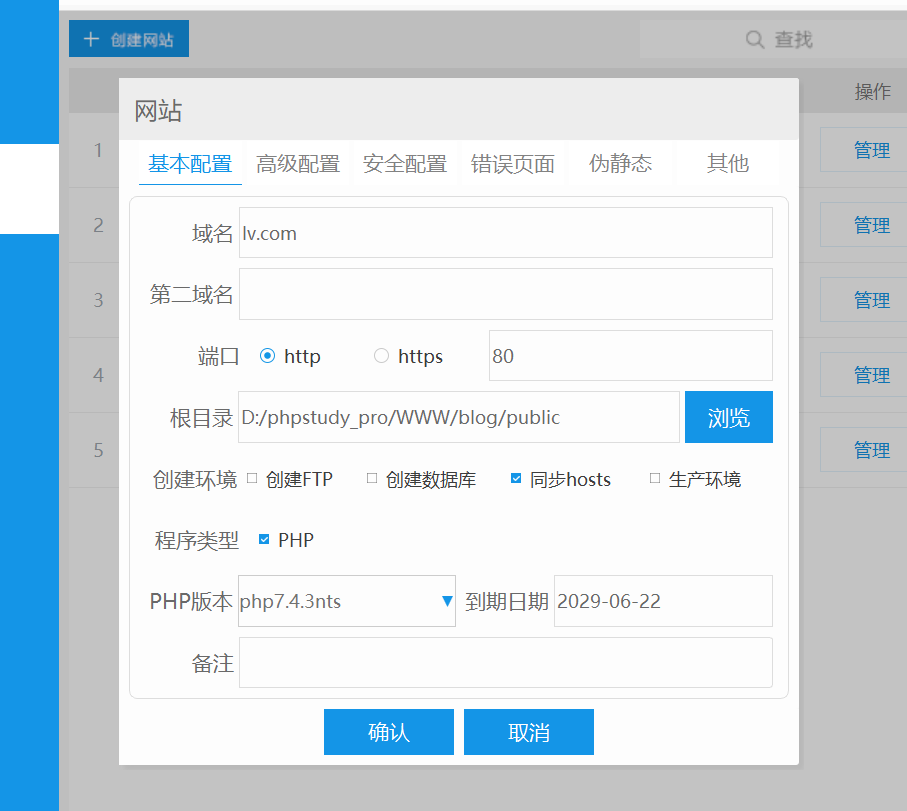
laravel8框架windows下安装运行
目录 1、安装前如果未安装先安装Composer 2、使用composer安装laravel8 3、使用内置服务器:8000 的命令去访问测试 4、使用本地环境运行phpstudy配置到public目录下 Laravel官网 Laravel 中文网 为 Web 工匠创造的 PHP 框架 安装 | 入门指南 |《Laravel 8 中文文档 8.x…...

如何快速判断IP被墙
IP被墙是指IP部分地区或者运营商无法被正常进行访问的一个情况。 被墙的原因有很多种不一一列举,由于被墙的时间短的为按周按月计算,时间长的则为按年计算,所以一般这种情况下只能选择更换IP。 检查办法: 第一,确认IP…...

vitest-前端单元测试
Vitest是一个轻量级、快速且功能强大的测试框架,特别适用于Vite项目,但也可以与其他前端项目(如使用webpack构建的项目)集成使用。Vitest提供极速的测试体验,并包含一系列用于编写和组织测试用例的API,如de…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
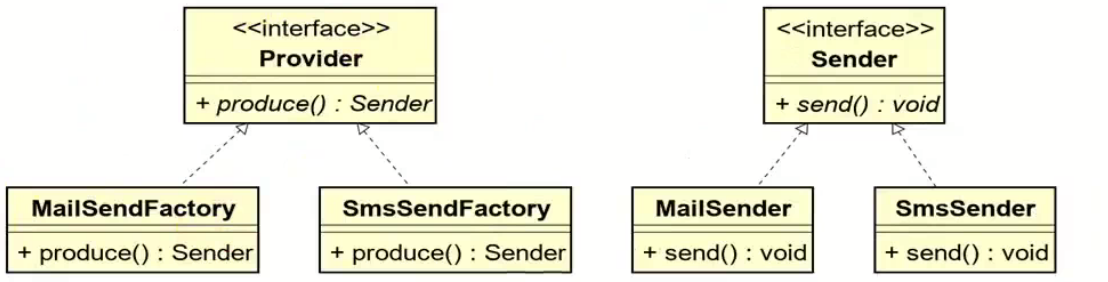
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

关于 ffmpeg设置摄像头报错“Could not set video options” 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/148515355 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
