代码随想录算法训练营第五十一天|LeetCode72 编辑距离、LeetCode647 回文子串、LeetCode516 最长回文子序列、动态规划的小总结
题1:
指路:72. 编辑距离 - 力扣(LeetCode)
思路与代码:
关于dp数组的定义,我们定义一个二维数组dp[i][j],其含义为以i-1为结尾的字符串word1和以j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。关于递推公式,如果数组1和数组2中内容相等,此时无须做任何操作,就等于下标为i-1和j-1的编辑距离,也就是dp[i][j]=dp[i-1][j-1]。当数组1和数组2中内容不同时,此时有三种操作,增、删、改。注意:当word1和word2中内容不相同时,不一定是单单改变其中一个变成另一个,也可以选择两者同时改变向对方靠近。删除word1的一个字符是dp[i-1][j]+1,替换字符为dp[i-1][j-1]+1,删除word2中字符(相对于word1为增加字符)即为dp[i][j-1]+1,取最小值即为 dp[i][j] = min({dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]}) + 1。那么在初始化环节,dp[i][0]的含义为以下标i-1为结尾的字符串word1和空字符串word2的最近编辑距离为dp[i][0],得到dp[i][0]=i,同理dp[0][j]=j。对于遍历顺序,很显然是从上到下从左到右,最后打印即可。代码如下:
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];}else {dp[i][j] = min({dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]}) + 1;}}}return dp[word1.size()][word2.size()];}
};题2:
指路:647. 回文子串 - 力扣(LeetCode)
思路与代码:
定义一个数组dp[i][j],其含义为在i和j的范围内如果i和j对应的值相等且子串如果是回文串那么这个以i和j为范围的字符串就是回文子串,其中分为三种情况,首先,i和j相等,那么显然这个字符串就是只有一个字符的字符串,肯定是一个回文串,遇到符合条件的回文串时计数器加1;其次如果i和j相差为1,也就是i和j相邻,此时如果s[i]等于s[j]那么这也是一个回文字符串;最后一种情况为i和j相差大于1,也就是它们之中有一个子串,此时将i定义为数组始位置,j定义为尾位置,在判断s[i]等于s[j]后,再进一步将i和j各往前移位一位,也就是i+1和j-1的位置,如果也成立继续判断得到回文子串的判断。注意,我们在i和j位置的数值也要判断的是i+1和j-1的位置的数值,那么在二维数组中对应的位置就是[i,j]的左下方位置,换句话来说,由左下方向右上方判断,也就是从左到右从下往上循环。最后输出即可。
class Solution {
public:int countSubstrings(string s) {if (s.size() <= 1) return s.size();vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) {result++;dp[i][j] = true;}else if (dp[i + 1][j - 1]) {result++;dp[i][j] = true;}}}}return result;}
};题3:
指路:516. 最长回文子序列 - 力扣(LeetCode)
思路与代码:
本题与上题的区别在于子串和子序列的区别,子串须连续,子序列则不需要。定义一个数组dp[i][j],其含义为字符串s[i, j]范围内最长的回文子序列的长度为d[i][j]。递推公式中,依旧是回文,判断s[i]与s[j]的相等状况就好。如果二者相同那么dp[i][j]=dp[i+1][j-1]+2(加2是因为首尾元素也是回文子序列的一部分),如果二者不相同则说明首尾元素不能同时加入子序列的队伍,那么尝试首尾元素分开添加,取较大值即可,即dp[i][j]=max(dp[i+1][j], dp[i][j-1])。这里的遍历顺序如上题所言,从下往上从左往右,最后打印即可。代码如下:
class Solution {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;}else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][s.size() - 1];}
};动态规划的小总结:
呼~动态规划终于告一段落了,感觉比起子序列问题我更喜欢股票类问题。但是无外乎就五步,定义dp数组及其定义,推断递推公式,初始化dp数组,确定遍历顺序最后打印dp数组。好累,先这样。
相关文章:

代码随想录算法训练营第五十一天|LeetCode72 编辑距离、LeetCode647 回文子串、LeetCode516 最长回文子序列、动态规划的小总结
题1: 指路:72. 编辑距离 - 力扣(LeetCode) 思路与代码: 关于dp数组的定义,我们定义一个二维数组dp[i][j],其含义为以i-1为结尾的字符串word1和以j-1为结尾的字符串word2,最近编辑…...

sessionStorage 能在多个标签页之间共享数据吗?
🧑💻 写在开头 点赞 收藏 学会🤣🤣🤣 最近,我的一个朋友在面试中被一个关于 sessionStorage 的问题难住了。我们来聊聊这个话题。 sessionStorage 能在多个标签页之间共享数据吗? 在回答…...

鸿蒙期末项目(完结)
两天仅睡3个小时的努力奋斗之下,终于写完了这个无比拉跨的项目,最后一篇博客总体展示一下本项目运行效果兼测试,随后就是答辩被同学乱沙(悲 刚打开软件,会看到如下欢迎界面,介绍本app的功能和优点 随后我们…...

【Linux】对共享库加载问题的深入理解——基本原理概述
原理概述 【linux】详解——库-CSDN博客 共享库被加载后,系统会为该共享库创建一个结构,这个结构体中的字段描述了库的各种属性。在内存中可能会加载很多库,每一个库都用一个结构体描述。把这些结构体用一些数据结构管理起来,系…...

easyui的topjui前端框架使用指南
博主今天也是第一次点开easyui的商业搜权页面,之前虽然一直在使用easyui前端框架(easyui是我最喜欢的前端ui框架),但是都是使用的免费版。 然后就发现了easyui的开发公司居然基于easyui开发出了一个新的前端框架,于是我…...
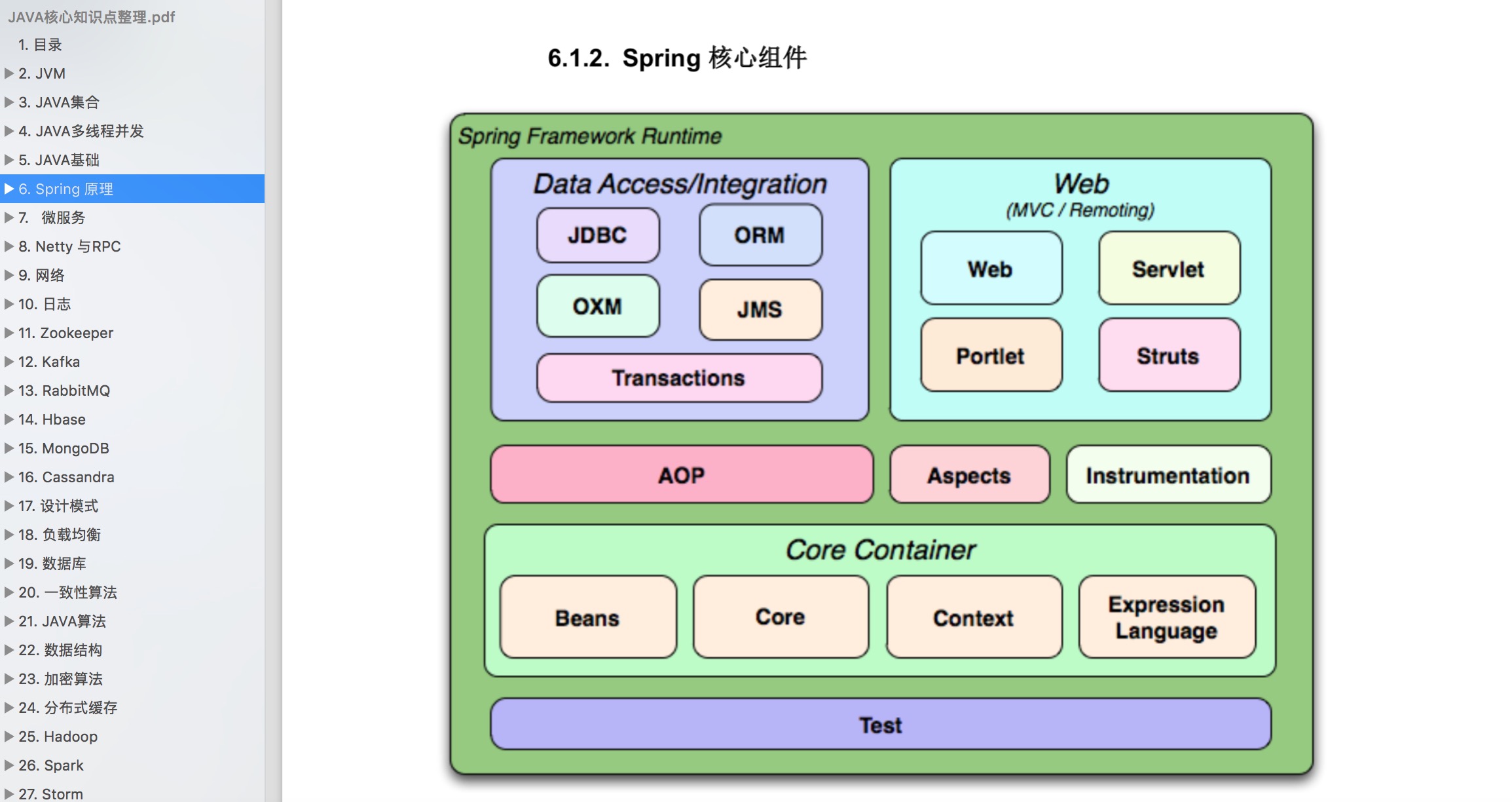
Java中的程序异常处理介绍
一、异常处理机制 Java提供了更加优秀的解决办法:异常处理机制。 异常处理机制能让程序在异常发生时,按照代码的预先设定的异常处理逻辑,针对性地处理异常,让程序尽最大可能恢复正常并继续执行,且保持代码的清晰。 Ja…...

Gradle学习-3 Gradle插件
1、Gredle插件是什么 Gradle插件是用于扩展和增强Gradle构建系统的功能模块通过插件,Gradle可以执行各种构建任务,如编译代码、打包应用、运行测试等 Gradle插件主要分为:二进制插件、脚本插件 二进制插件二进制插件是预编译的、可以复用的…...
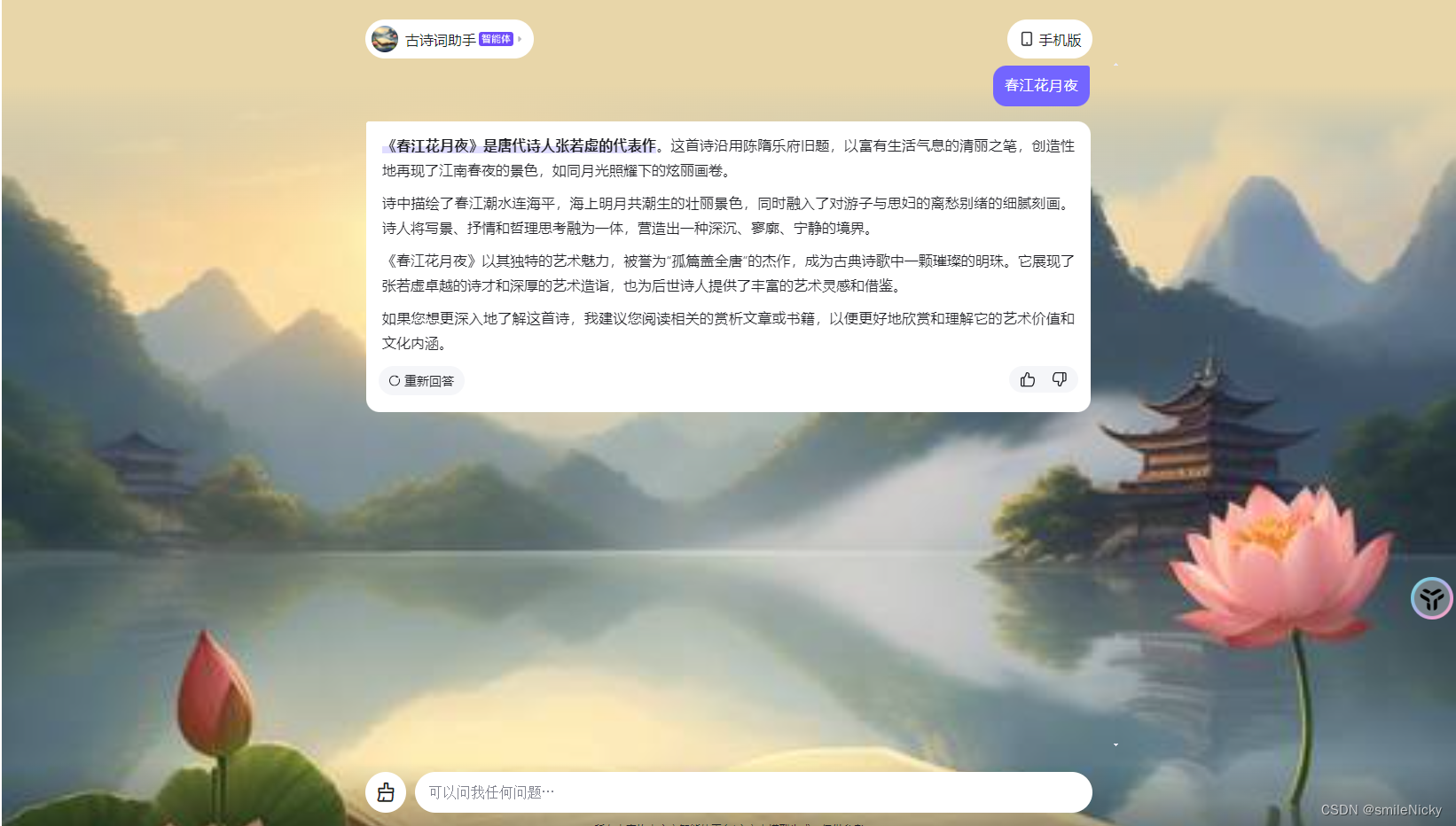
百度文心智能体,创建属于自己的智能体应用
百度文心智能体平台为你开启。百度文心智能体平台,创建属于自己的智能体应用。百度文心智能体平台是百度旗下的智能AI平台,集成了先进的自然语言处理技术和人工智能技术,可以用来创建属于自己的智能体应用,访问官网链接࿱…...
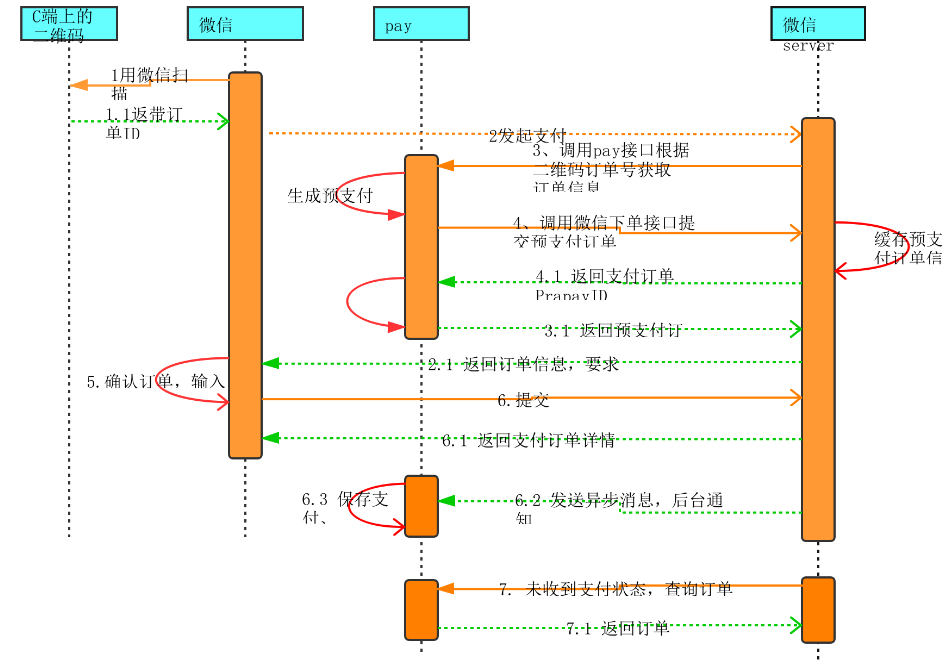
【软件测试】白盒测试与接口测试详解
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 一、什么是白盒测试 白盒测试是一种测试策略,这种策略允许我们检查程序的内部结构&a…...

【SpringBoot Web框架实战教程】03 SpingBoot 获取 http 请求参数
不积跬步,无以至千里;不积小流,无以成江海。大家好,我是闲鹤,微信:xxh_1459,十多年开发、架构经验,先后在华为、迅雷服役过,也在高校从事教学3年;目前已创业了…...

Mac14.1.2 M1芯片免费读写ntfs硬盘-亲测有效,免费!!!
1. 安装homebrew 打开终端,使用以下命令 /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)" 根据提示逐步完成即可,镜像选择我这里都是保持1的选项。 2. 重启终端 安装完成homebrew后,需…...

手写SpringMVC之ApplicationContextListener
什么是Spring MVC? Spring Web MVC是基于Servlet API构建的原始Web框架,从一开始就包含在Spring Framework中。正式名称“Spring Web MVC”来自其源模块的名称( spring-webmvc ),但它通常被称为“Spring MVC”。 手写…...
Paimon 在汽车之家的业务实践
汽车之家基于Paimon的实践 摘要:本文分享自汽车之家的王刚、范文、李乾⽼师。介绍了汽车之家基于 Paimon 的一些实践,和一些背景。内容主要为以下四部分: 一、背景 二、业务实践 三、paimon 优化实践 四、未来规划 一、背景 在使用Paimon之前…...

2024-06-27 问AI: 介绍一下 LLM building process
文心一言 LLM(Large Language Model,大语言模型)的构建过程是一个复杂且资源密集的任务,涉及多个关键步骤。以下是LLM构建过程的主要阶段,以及每个阶段的一些关键考虑因素: 数据收集与预处理:…...

猫也有自动厕所上了吗?自费分享好用的智能猫砂盆,看完不亏。
还有人在用普通猫砂盘吗?之前我也是用的普通猫砂盘,但我发现只要我在上班时间,我就无法顾忌到小猫的便便,但又不想回家就闻到一股臭味,更何况现在夏天也快到了,便便残留一会就会发酵发臭,导致生…...
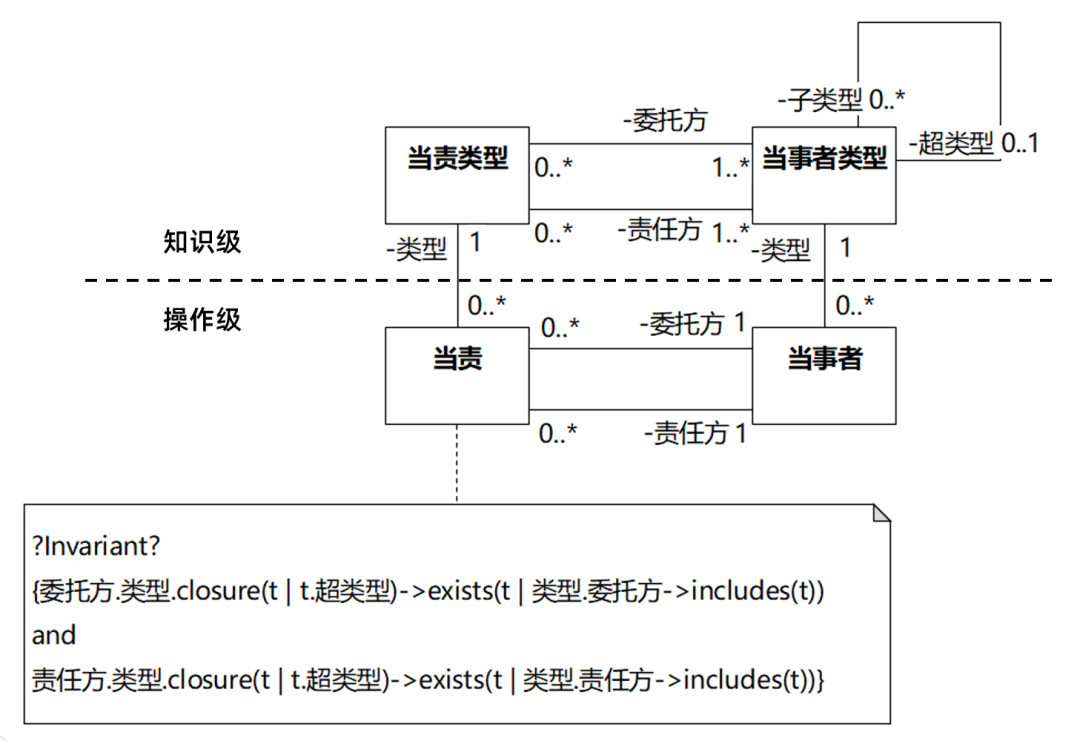
《分析模式》漫谈07-怎样把一张图从不严谨改到严谨
DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 下图是《分析模式》原书第2章的图2.10,里面有一些错误和考虑不周的地方: 2004中译本和2020中译本的翻译如下: 基本上都是照搬,没有改过…...

纯干货丨知乎广告投放流程和避坑攻略
精准有效的广告投放企业获客的关键,知乎作为中国最大的知识分享平台,拥有着高质量的用户群体和高度的用户粘性,为广告主提供了独一无二的品牌传播与产品推广平台。然而,如何在知乎上高效、精准地进行广告投放,避免不必…...
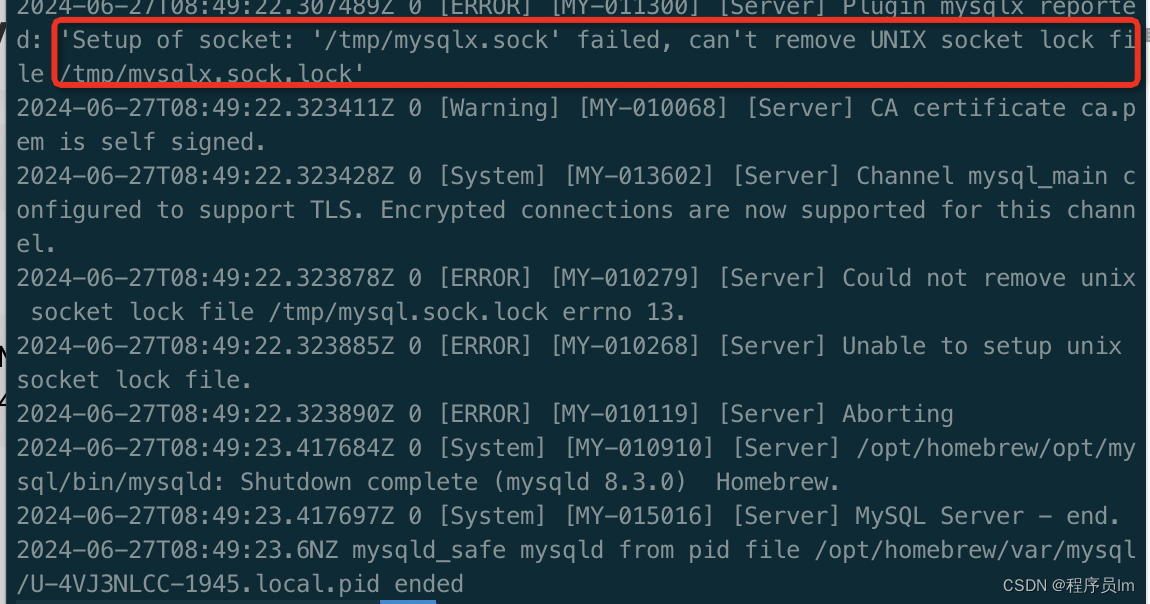
mac 安装mysql启动报错 ERROR!The server quit without update PID file
发现问题: mac安装mysql初次启动报错: 一般出现这种问题,大多是文件夹权限,或者以前安装mysql卸载不干净导致。首先需要先确定问题出在哪?根据提示我们可以打开mysql的启动目录,查看启动日志。 问题解决&a…...

TypeScrip环境安装与基础
TS环境安装与基础 文章目录 一、什么是TypeScript(微软开发的)二、TypeScript的特性三、环境安装node安装配置详解(常用:outDir,strict ) 四、注释方式五、数据类型 一、什么是TypeScript(微软开…...

6.27学习总结
一、高数 1、斯托克斯公式(曲线<->曲面):看清顺时针(负)/逆时针(正) 2、曲面方程变二重积分: 前、上、右:正; 后、下、左:负; 3…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
