统计学 多元线性回归
文章目录
- 统计学 多元线性回归
- 多元线性回归模型
- 拟合优度
- 显著性检验
- 线性关系检验
- 回归系数检验
- 多重共线性及其处理
- 多重共线性的问题
- 多重共线性的识别与处理
- 变量选择
- 利用回归方程进行预测
- 哑变量回归
统计学 多元线性回归
多元线性回归模型
多元线性回归模型:设因变量为 yyy ,kkk 个自变量分别为 x1x_1x1 ,x2x_2x2 ,⋯\cdots⋯ xkx_kxk ,一般表示形式为:
y=β0+β1x1+β2x2+⋯+βkxk+εy=\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_kx_k+\varepsilon y=β0+β1x1+β2x2+⋯+βkxk+ε
这里对误差项 ε\varepsilonε 同样有三个基本的假定:
- 正态性:ε\varepsilonε 是一个服从期望为 0 的正态分布的随机变量,意味着给定 x1x_1x1 ,x2x_2x2 ,⋯\cdots⋯ xkx_kxk 的值,yyy 的期望值为 E(y)=β0+β1x1+⋯+βkxkE(y)=\beta_0+\beta_1x_1+\cdots+\beta_kx_kE(y)=β0+β1x1+⋯+βkxk ;
- 方差齐性:对于自变量 x1x_1x1 ,x2x_2x2 ,⋯\cdots⋯ xkx_kxk 的所有值,ε\varepsilonε 的方差 σ2\sigma^2σ2 都相同 ;
- 独立性:对于自变量 x1x_1x1 ,x2x_2x2 ,⋯\cdots⋯ xkx_kxk 的不同值,ε\varepsilonε 之间相互独立
最小二乘法:根据残差的平方和最小,估计多元回归模型中的参数 β^0\hat\beta_0β^0 ,β^1\hat\beta_1β^1 ,⋯\cdots⋯ β^k\hat\beta_kβ^k :
Q=∑(yi−y^i)2=∑(yi−β^0−β^1x1−⋯−β^kxk)2=minQ=\sum(y_i-\hat y_i)^2=\sum(y_i-\hat\beta_0-\hat\beta_1x_1-\cdots-\hat\beta_kx_k)^2=\min Q=∑(yi−y^i)2=∑(yi−β^0−β^1x1−⋯−β^kxk)2=min
标准化回归方程:在计算最小二乘法前,对因变量和各个自变量进行标准化处理,再计算回归方程,其中标准化回归系数记作 βˉ\bar\betaβˉ ;比较不同的 βˉi\bar\beta_iβˉi 我们可以得到对因变量来说最重要的变量
拟合优度
拟合优度主要由多重决定系数或估计标准误差等统计量来评价。
多重决定系数:同样将总平方和分解为回归平方和加误差平方和:
SST=∑(yi−yˉ)2=SSR+SSE=∑(yi^−yˉ)2+∑(yi−yi^)2SST=\sum(y_{i}-\bar{y})^2=SSR+SSE=\sum(\hat{y_{i}}-\bar{y})^{2}+\sum(y_{i}-\hat{y_{i}})^{2} SST=∑(yi−yˉ)2=SSR+SSE=∑(yi^−yˉ)2+∑(yi−yi^)2
多重决定系数 R2R^{2}R2 为:
R2=SSRSSTR^{2}=\frac{SSR}{SST} R2=SSTSSR
多重决定系数表示因变量 yyy 的总变差中被多个自变量所解释的比例;在多元线性回归中,自变量的个数将会影响到因变量中被估计回归方程所揭示的变差数量。即使再增加一个新的自变量,该自变量在统计上并不显著,也会导致多重决定系数 R2R^{2}R2 增大,因此我们引入调整的多重决定系数 Ra2R_{a}^{2}Ra2 :
Ra2=1−(1−R2)×n−1n−k−1R_{a}^{2}=1-(1-R^{2})\times \frac{n-1}{n-k-1} Ra2=1−(1−R2)×n−k−1n−1
其中 nnn 为样本数量,kkk 为自变量的个数;这样调整过后的多重决定系数总会小于原来的系数,不会因为自变量的个数增加而导致 R2R^{2}R2 越来越接近于 1;所以实际当中一般使用调整过后的多重决定系数进行评价。
估计标准误差:即残差平方和的平方根,是对误差项 ε\varepsilonε 的标准差 σ\sigmaσ 的一个估计值:
se=∑(yi−y^i)2n−k−1=SSEn−k−1s_e=\sqrt{\frac{\sum(y_i-\hat y_i)^2}{n-k-1}}=\sqrt{\frac{SSE}{n-k-1}} se=n−k−1∑(yi−y^i)2=n−k−1SSE
ses_ese 可解释为,根据自变量 x1x_1x1 ,x2x_2x2 ,⋯\cdots⋯ xkx_kxk 来预测因变量 yyy 时的平均预测误差
显著性检验
线性关系检验
线性关系检验:检验因变量 yyy 与 kkk 个自变量之间的关系是否显著,也称为总体显著性检验:
① 提出假设:
- H0H_0H0 :β1=β2=⋯=βk=0\beta_1=\beta_2=\cdots=\beta_k=0β1=β2=⋯=βk=0 (因变量 yyy 与 kkk 个自变量之间的关系不显著)
- H1H_1H1 :βi\beta_iβi 中至少有一个不为 0(因变量 yyy 与 kkk 个自变量之间的关系显著)
② 计算检验统计量(FFF 检验):
F=SSR/kSSE/(n−k−1)=MSRMSE∼F(k,n−k−1)F=\frac{SSR/k}{SSE/(n-k-1)}=\frac{MSR}{MSE}\sim F(k,\,n-k-1) F=SSE/(n−k−1)SSR/k=MSEMSR∼F(k,n−k−1)
③ 作出决策,算出 PPP 值,根据显著性水平 α\alphaα 决定是否拒绝原假设
回归系数检验
回归系数检验:判断每个自变量对因变量的影响是否都显著,需要对每个回归系数 βi\beta_iβi 进行 ttt 检验:
① 提出假设:
- H0H_0H0 :βi=0\beta_i=0βi=0 (xix_ixi 对 yyy 的影响不显著)
- H1H_1H1 :βi≠0\beta_i\not=0βi=0 (xix_ixi 对 yyy 的影响显著)
② 计算检验统计量 ttt :
ti=β^isβ^i∼t(n−k−1)t_i=\frac{\hat{\beta}_i}{s_{\hat{\beta}_i}}\sim t(n-k-1) ti=sβ^iβ^i∼t(n−k−1)
其中 sβ^is_{\hat{\beta}_i}sβ^i 是回归系数 β^i\hat{\beta}_iβ^i 的抽样分布的标准差,计算公式为:(xj.ix_{j.i}xj.i 代表第 jjj 组自变量中的第 iii 个自变量,即每一组中的第 iii 个自变量)
sβi^=se∑(xj.i−xˉi)2s_{\hat{\beta_i}}=\frac{s_e}{\sqrt{\sum(x_{j.i}-\bar{x}_i)^2}} sβi^=∑(xj.i−xˉi)2se
多重共线性及其处理
多重共线性的问题
多重共线性:回归模型中两个或两个以上的自变量彼此相关
① 若 kkk 个自变量之间存在高度相关时,有可能造成某一个或几个回归系数通不过检验,但并不意味着没通过检验的那些自变量对因变量的影响就不显著,只是这些相关的自变量提供了多余的信息。例如通过了 FFF 检验但某些回归系数没有通过 t 检验,并不代表没有通过 t 检验的自变量对因变量的影响不显著,可能只是它的贡献与其他自变量的贡献重叠了;
② 多重共线性可能对回归系数的符号造成影响,有可能几个相关的自变量中,某些自变量的回归系数较大,导致另一些自变量要抵消一部分作用所以回归系数算出来是负的,但是并不意味着它们与因变量是负相关的关系;
多重共线性的识别与处理
识别方法:
① 对模型中各自变量之间的相关系数进行显著性检验,若存在某些自变量是显著相关的,那么可能存在多重共线性;
② 考察各回归系数的显著性,若通过 FFF 检验,而几乎所有的回归系数都没有通过 t 检验,那么就可能存在多重共线性
③ 分析回归系数的正负号,如果回归系数的正负号与预期(现实经验)相反,那么就可能存在多重共线性
④ 计算容忍度和方差扩大因子(VIF)来识别共线性:
tolerance=1−Ri2VIF=11−Ri2=1tolerancetolerance=1-R^2_i \\ VIF=\frac{1}{1-R_i^2}=\frac{1}{tolerance} tolerance=1−Ri2VIF=1−Ri21=tolerance1
其中 Ri2R_i^2Ri2 代表将第 iii 各自变量看作因变量,其他 k−1k-1k−1 个自变量对其造成影响的决定系数;容忍度越小,方差扩大因子越大(大于5或10),多重共线性越严重;
处理方法:
① 将一个或多个相关的自变量从模型中剔除,使得自变量之间尽量不相关
② 如果要在模型中保留所有自变量,则要避免对单个回归系数进行 t 检验,并且将对因变量 yyy 值的推断限定在自变量样本的范围内
③ 在建立模型之前有选择地确定进入模型的自变量
变量选择
在多重共线性的处理中,变量选择是有效方法。在建立多元线性回归模型时,不要试图引入更多的自变量,除非确实有必要。选择自变量的原则是:将某个自变量引入回归模型时,应当使残差平方和(SSE)有显著的降低,否则就没有必要。
变量选择的主要方法有:向前选择、向后剔除、逐步回归
向前选择:从没有自变量开始,按照步骤逐步选择自变量;特点是被选择的自变量不会再被剔除。
- 分别拟合因变量 yyy 与 kkk 个自变量的一元线性回归模型,找到 FFF 统计量最大(PPP 值最小,代表线性关系越显著)的模型对应的自变量 xix_ixi ,将其引入模型;
- 分别拟合因变量 yyy 与 k−1k-1k−1 个新的自变量 xi+x1,xi+x2,⋯,xi+xkx_i+x_1,\,x_i+x_2,\,\cdots,\,x_i+x_kxi+x1,xi+x2,⋯,xi+xk 进行一元线性回归的 FFF 检验,找到 FFF 统计量最大(PPP 值最小,代表线性关系越显著)的模型对应的自变量 xjx_jxj ,将其引入模型;
- 重复,直到满足某种条件:达到预设的变量数量;达到预设的显著性水平;达到算法的最大迭代次数;模型预测性能(SSE)不能再提升
向后剔除:从完整模型开始,按照步骤逐步剔除自变量;特点是被剔除的自变量不会再进入模型。
- 计算完整的多元回归模型;
- 分别拟合因变量 yyy 与剔除每一个自变量、保留剩下的 k−1k-1k−1 个自变量时的回归模型,挑出 FFF 统计量最大(PPP 值最小 / SSE 增加最少)的模型,则保留该模型的 k−1k-1k−1 个自变量;
- 重复,直到满足某种条件:达到预设的变量数量;达到预设的显著性水平;达到算法的最大迭代次数;模型预测性能(SSE)不能再提升
逐步回归:结合前两种方法:开始时与向前选择法相同,但增加一个自变量后,要对模型中所有自变量进行考察,若有些自变量对模型的影响变得不显著,则将其剔除,直到增加变量已经不能导致 SSESSESSE 显著减少。特点是加入模型的自变量也可能被剔除,被剔除的自变量也可能重新加入模型中。
利用回归方程进行预测
书上没给公式耶,因为比较复杂,但是跟一元线性回归一样,可以进行点估计、平均值的置信区间估计和个别值是预测区间估计。可以借助软件来完成。
哑变量回归
哑变量:又称虚拟变量,即代码化的定性自变量(一位热键,OneHotEncode);如果定性自变量又 kkk 个水平,需要在回归模型中引入 k−1k-1k−1 个哑变量:
x1={1水平10其他水平x2={1水平20其他水平⋯xk−1={1水平k−10其他水平x_1=\left\{ \begin{array}{ll} 1 & 水平\,1 \\ 0 & 其他水平 \end{array} \right. \quad x_2=\left\{ \begin{array}{ll} 1 & 水平\,2 \\ 0 & 其他水平 \end{array} \right. \quad\cdots\quad x_{k-1}=\left\{ \begin{array}{ll} 1 & 水平\,k-1 \\ 0 & 其他水平 \end{array} \right. x1={10水平1其他水平x2={10水平2其他水平⋯xk−1={10水平k−1其他水平
只有一个定性自变量且处理有两种(不论数值自变量有几种)的情况,例如性别用 1 和 0 编码,那么 β0\beta_0β0 总是代表哑变量值 0 所对应的那个类别变量水平的平均值,而 βi\beta_iβi (即定性自变对应的回归系数)总是代表哑变量值 1 所对应的那个类别变量水平的平均值与哑变量值 0 所对应的那个类别变量水平的平均值的差值。
相关文章:

统计学 多元线性回归
文章目录统计学 多元线性回归多元线性回归模型拟合优度显著性检验线性关系检验回归系数检验多重共线性及其处理多重共线性的问题多重共线性的识别与处理变量选择利用回归方程进行预测哑变量回归统计学 多元线性回归 多元线性回归模型 多元线性回归模型:设因变量为…...
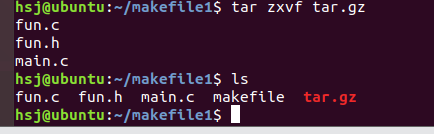
tar和gzip压缩和解压
打包和压缩的区别:打包:将多文件 封装在一起压缩:将多文件 封装在一起 通过特定的算法 将冗余的数据 进行删除tar默认是打包命令,如果想用tar进行压缩 必须加选项1、gzip格式压缩:tar zcvf 压缩包包名 文件1 文件2 文件…...

搭建Docker企业私有仓库
什么是仓库 仓库(Repository)是存储和分发 Docker 镜像的地方。镜像仓库类似于代码仓库,Docker Hub 的命名来自 GitHub,Github 是我们常用的代码存储和分发的地方。同样 Docker Hub 是用来提供 Docker 镜像存储和分发的地方。 谈…...

[NOIP2009 提高组] 最优贸易(C++,tarjan,topo,DP)
题目描述 $C 国有国有国有 n 个大城市和个大城市和个大城市和 m$ 条道路,每条道路连接这 nnn个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mmm 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的…...

计算机网络:移动IP
移动IP相关概念 移动IP技术是移动结点(计算机/服务器)以固体的网络IP地址,实现跨越不同网段的漫游功能,并保证了基于网络IP的网络权限在漫游中不发生任何改变。移动结点:具有永久IP地址的设备。归属代理(本…...

binutils工具集——GNU binutils工具集简介
以下内容源于网络资源的学习与整理,如有侵权请告知删除。 GNU binutils是一个二进制工具集,主要包括: ld,GNU链接器。as,GNU汇编器。addr2line,把地址转化为文件名和行号。nm,列出目标文件的符…...
有趣应用)
Golang编译选项(ldflags)有趣应用
本文介绍如何在构建时使用ldflags选项给Golang应用程序注入变量,用于给Go可执行文件增加版本标识或GIT提交摘要等信息。 应用程序的版本信息 我们首先查看Docker Cli 包含的提交信息: docker version 返回结果: Server: Docker Engine - Co…...
 在AIR32F103上移植微雪墨水屏驱动)
AIR32F103(十一) 在AIR32F103上移植微雪墨水屏驱动
目录 AIR32F103(一) 合宙AIR32F103CBT6开发板上手报告AIR32F103(二) Linux环境和LibOpenCM3项目模板AIR32F103(三) Linux环境基于标准外设库的项目模板AIR32F103(四) 27倍频216MHz,CoreMark跑分测试AIR32F103(五) FreeRTOSv202112核心库的集成和示例代码AIR32F103(六) ADC,I2S…...

Uipath Excel 自动化基础系列文章
Uipath Excel 自动化基础系列文章已发布到CSDN,网址:https://blog.csdn.net/Marshaljun?typeblog (3月份会在CSDN博客发布Uipath Excel 实战课程及经验分享) Uipath Studio流程设计器介绍 https://blog.csdn.net/Marshaljun/article/details/128699022 Uipath St…...

神经网络优化器之随机梯度下降法的理解
随机梯度下降法(SGD)随机梯度下降方法,在每次更新时用1个样本,随机也就是说我们用样本中的一个例子来近似我所有的样本,由于计算得到的并不是准确的一个梯度,因而不是全局最优的。但是相比于批量梯度&#…...
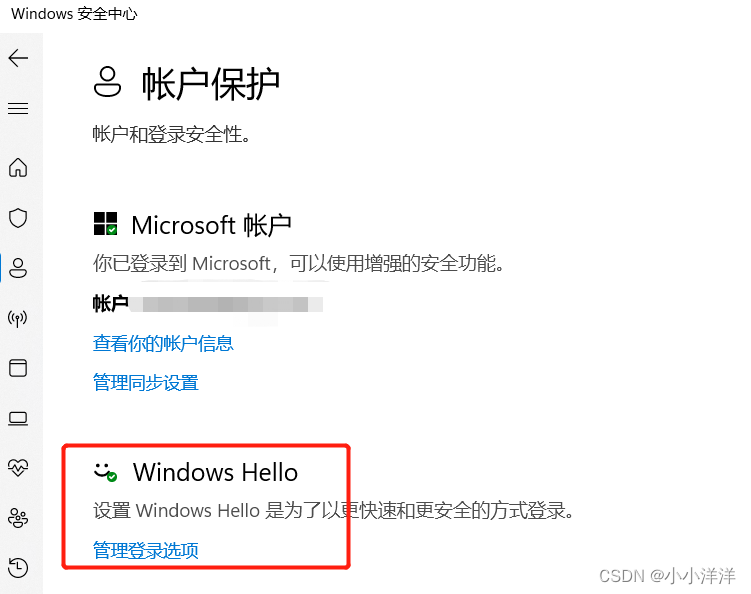
记录一次WIN11开机在登录页面循环的问题
记录一次由于未进行win密码设置,导致开机后卡在登录界面无法登录进去的问题。最后完美解决了。 1. 背景 开机后,显示用户登录界面,但是和以往不同,没有了密码输入框,只有一个“登录”按钮孤零零地显示在屏幕中间&…...

始终从最不易改变的方面开始
在你刚开始新工作、转换职业或者是加入新项目时,始终从最不易改变的方面开始。 在工作中,这可能意味着与团队成员建立关系,了解公司的流程和文化,或者熟悉公司的产品或服务。 在一项新项目中,这可能意味着了解项目范…...

4、Httpclient源码解析之HTTP协议
初始化CloseableHttpClient过程中涉及ExecChainHandler & DefaultHttpProcessor,即典型客户端责任链中的请求执行处理器。 责任链中各节点涉及请求处理器【ExecChainHandler】顺序如下:RedirectExec、ContentCompressionExec、HttpRequestRetryExec…...
浏览器并发行为记录
使用nodejs koa起一个服务,使请求延时返回。 服务端代码 /** 延时 */ exports.timeoutTestData async function (ctx) {console.log(get query:, ctx.request.query);const query ctx.request.query;let timeout query.timeout || 2000;await new Promise(res…...

工厂模式与抽象工厂
原理:逻辑和业务全部封装 不需要细节 只要结果 示例: # 简单工厂 class SimpleFactory:# 产品staticmethoddef product(name):return nameif __name__ "__main__":product SimpleFactory.product("Gitee")print(product) 装饰器…...

什么?你不知道 ConcurrentHashMap 的 kv 不能为 null?
一、背景 最近设计某个类库时使用了 ConcurrentHashMap 最后遇到了 value 为 null 时报了空指针异常的坑。 本文想探讨下以下几个问题: (1) Map接口的常见子类的 kv 对 null 的支持情况。 (2)为什么 ConcurrentHashM…...

SQL复习04 | 复杂查询
1. 视图 视图和表的区别: 表保存的是实际的数据视图保存的是SELECT语句 视图的优点: 视图无需保存数据,可节省存储设备的容量可以将频繁使用的SELECT语句保存成视图,可大大提高效率 1.1 创建视图 CREATE VIEW 视图名称&…...
)
【面试题】Java面试题汇总(无解答)
此内容会持续补充。。。 基础 short s1 1; s1 s1 1;有错吗? short s1 1; s1 1; 有错吗?String str”aaa”,与 String strnew String(“aaa”)一样吗?String 和 StringBuilder、StringBuffer 的区别?Sring最大能存多大内容?…...
)
C++---背包模型---收服精灵(每日一道算法2023.3.11)
注意事项: 本题是"动态规划—01背包"的扩展题,优化的思路不多赘述,dp思路会稍有不同,下面详细讲解。 本题偏向阅读理解,给每种变量归类起名字很有帮助哦。 切记先看思路,再看代码。(大…...

day30_JS
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、BOM 三、定时器 四、正则表达式 零、 复习昨日 事件 事件绑定方式鼠标事件 onmouseoveronmouseoutonmousemove 键盘事件 onkeydownonkeyupon…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
