代码随想录训练营Day51
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、不同的子序列
- 二、两个字符串的删除操作
- 三、编辑距离
前言
提示:这里可以添加本文要记录的大概内容:
今天是跟着代码随想录刷题的第51天,主要学习了不同的子序列、两个字符串的删除操作、编辑距离
提示:以下是本篇文章正文内容,下面案例可供参考
一、不同的子序列
思路:
这道题的dp[i][j]是[0,i-1]的s最多能有多少种方式组合成[0,j-1],初始化dp[0][i]空字符串组成不了,所以是0,dp[i][0]是字符串中找多少个方式是空字符串,那就是全部删除掉就可以了,所以只有这一种,至于dp[0][0]空字符串本身就是空字符串不用删减所以也是一种,递推公式如果s[i-1]==t[j-1],则dp[i][j]=dp[i-1][j-1]+dp[i-1][j]中, dp[i-1][j-1]是最后一个i来的时候,一共多了多少种组合,dp[i-1][j]是上一个有多少种组合,所以合理,如果最后一个元素不相等,就说明加不加最后一个元素没区别,直接等于dp[i-1][j]
代码:
class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size()+1,vector<uint64_t>(t.size()+1,0));for(int i=0;i<=s.size();i++) dp[i][0]=1;for(int i=1;i<=t.size();i++) dp[0][i]=0;for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]){dp[i][j]=dp[i-1][j-1]+dp[i-1][j];//dp[i-1][j-1]是最后一个i来的时候,一共多了多少种组合,dp[i-1][j]是上一个有多少种组合}else{dp[i][j]=dp[i-1][j];}}}return dp[s.size()][t.size()];}
};二、两个字符串的删除操作
思路:
关键是dp数组的定义,dp[i][j]表示[0,i-1]和[0,j-1]两个字符串如果要变成相同所需要的最小步数,这里i-1和j-1是因为初始化比较简单,递推公式推导见文中的注释
代码:
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<uint64_t>> dp(word1.size()+1,vector<uint64_t>(word2.size()+1,0));//dp[i][j]表示[0,i-1]和[0,j-1]两个字符串如果要变成相同所需要的最小步数for(int i=0;i<=word1.size();i++)//初始化{dp[i][0]=i;}for(int i=0;i<=word2.size();i++)//初始化{dp[0][i]=i;}for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]){dp[i][j]=dp[i-1][j-1]; //如果最后两个是一样的就说明变成一样需要的步数和去掉这两个没区别 }else{dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//如果最后两个不一样,就看到底是哪个变动需要的步数,变动的那个把那行给去掉一个加上去掉需要的步数1}}}return dp[word1.size()][word2.size()];}
};三、编辑距离
思路:
如果最后两个不一样,可能是增加删减或者替换,先讲一下删除元素,删除元素就是,我要删除的那个元素不管,上面缺一个元素i-1和下面j先操作,操作完以后,把上面那个元素删除就好了,增加和删减其实一样,因为我增加去迎合你,是不是就相当于你减去一个迎合我的操作是一样的,如果是替换,那么我结尾的元素都不用管了,把i-1,j-1的元素操作完成,然后最后一对两个元素换成一样的一步骤就可以,所以是dp[i-1][j-1]+1
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<uint64_t>> dp(word1.size()+1,vector<uint64_t>(word2.size()+1,0));//dp[i][j]表示[0,i-1]和[0,j-1]两个字符串如果要变成相同所需要的最小步数for(int i=0;i<=word1.size();i++)//初始化{dp[i][0]=i;}for(int i=0;i<=word2.size();i++)//初始化{dp[0][i]=i;}for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]){dp[i][j]=dp[i-1][j-1]; //如果最后两个是一样的就说明变成一样需要的步数和去掉这两个没区别 }else{dp[i][j]=min(min(dp[i-1][j]+1,dp[i][j-1]+1),dp[i-1][j-1]+1);//如果最后两个不一样,可能是增加删减或者替换}}}return dp[word1.size()][word2.size()];}
};相关文章:

代码随想录训练营Day51
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、不同的子序列二、两个字符串的删除操作三、编辑距离 前言 提示:这里可以添加本文要记录的大概内容: 今天是跟着代码随想录刷题的第…...

C#上位机与PLC
在工业自动化的舞台上,C#上位机与PLC之间的通信是一曲精妙绝伦的交响乐。今天,我们将一起揭开C#上位机与PLC通信的三种神秘实现方法,探索它们如何共同谱写出高效、稳定、灵活的工业自动化乐章。 序幕:通信的“前奏” 在深入了解…...

CVE-2018-8120漏洞提权:Windows 7的安全剖析与实战应用
CVE-2018-8120漏洞提权:Windows 7的安全剖析与实战应用 在网络安全的世界里,漏洞利用常常是攻击者用来获取系统控制权的捷径。2018年发现的CVE-2018-8120漏洞,针对Windows 7操作系统,提供了一个这样的途径。本文将深入分析这一漏…...
Python-正则表达式
目录 一、打开正则表达式 二、正则表达式的使用 1、限定符 (1)x*:*表示它前面的字符y 可以有0个或多个; (2)x:表示它前面的字符可以出现一次以上;(只可以匹配多次&…...
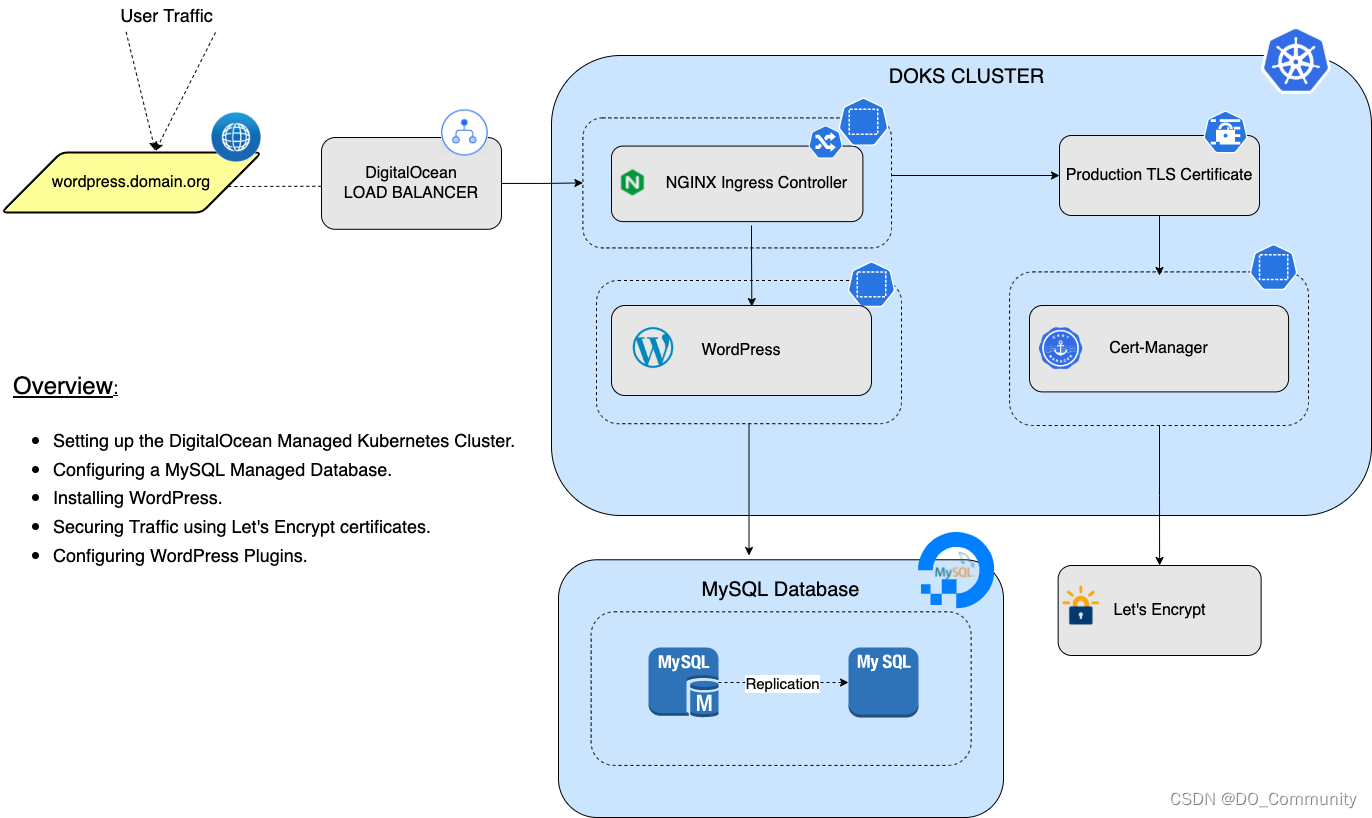
教程:在 Kubernetes 集群上部署 WordPress 网站
WordPress 是专为每个人设计的开源软件,强调创建网站、博客或应用程序的可访问性、性能、安全性和易用性。WordPress 是一个基于 PHP 的内容管理系统(CMS),使用 MySQL 作为数据存储,目前很多网站、电商独立站、个人博客…...
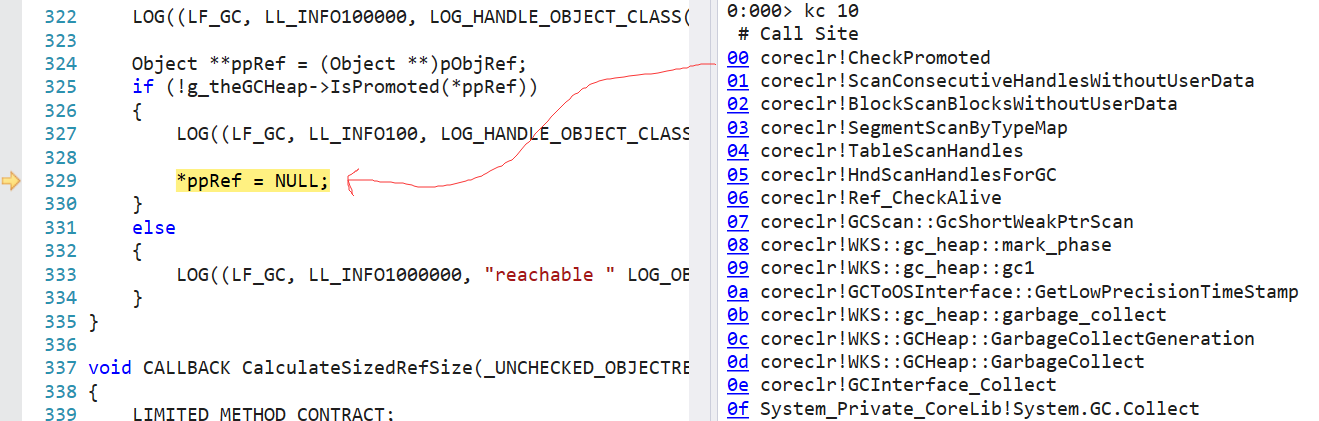
聊一聊 C# 弱引用 底层是怎么玩的
一:背景 1. 讲故事 最近在分析dump时,发现有程序的卡死和WeakReference有关,在以前只知道怎么用,但不清楚底层逻辑走向是什么样的,借着这个dump的契机来简单研究下。 二:弱引用的玩法 1. 一些基础概念 …...
)
蜘蛛池规矩采集优化与运用技巧 什么是蜘蛛池/SEO蜘蛛池怎么养?(蜘蛛池新手入门虚良SEO)
作为一名网络内容修改,我常常需求从各种网站上收集文章并转载到咱们的网站上。而在这个过程中,我深深感受到了蜘蛛池对我的帮助。今日,我就来共享一下我对蜘蛛池收集规矩的亲自感受。 归纳 本文将分9个方面具体介绍蜘蛛池收集规矩的长处和运…...
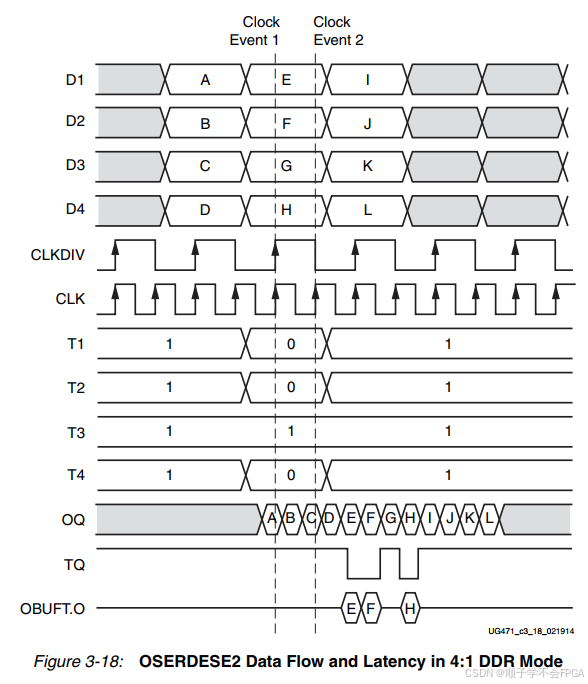
SerDes介绍以及原语使用介绍(1)OSERDESE2
文章目录 前言:为什么需要serdes一、OSERDESE2框图二、OSERDESE2端口信号二、OSERDESE2原语参数三、OSERDESE2时序3.1、SDR模式3.2、DDR模式3.3、DDR模式下三态传输 前言:为什么需要serdes 需要 SerDes(串行器/解串器)主要是为了…...

基于单片机和组态王的温度监控系统的设计
摘 要 : 介绍了以 MSP430 单片机为核心 , 建立基于 DS18B20 和组态王的温度采集和监控系统。主要研究了单片机和组态王的通用通讯协议。按照 KingView 提供的通信协议 , 设计组态王与单片机的通信程序 , 实现了组态王与M SP430 单片机的直接串行通讯。在中药提取装置的…...

unity 导入的模型设置讲解
咱们先讲Model这一栏 Model Scene:场景级属性,例如是否导入灯光和照相机,以及使用什么比例因子。 Scale Factor:缩放因子(也就是模型导入后大小如果小了或者大了在这里直接改是相当于该模型的大小的,而且在…...

汽车 vSOC安全运营管理平台开发解决方案
汽车 vSOC 安全解决方案 一、引言 随着汽车行业的快速发展,汽车的智能化和互联化程度越来越高,汽车网络安全问题也日益凸显。汽车 vSOC(Vehicle Security Operations Center)作为汽车网络安全的重要组成部分,其作用越来越受到重视。本方案旨在提供一套可实施落地的汽车 vS…...

python 第三方库
一、什么是第三方库 python的三方库指的是,需要通过pip install 安装后才能使用的 python 工具 三方库有很多: 做web自动化测试的库:selenium单元测试框架:pytest、unittest做app自动化测试:Python-Appium-Client做接…...
VMware Workstation环境下,DHCP服务的安装配置,用ubuntu来测试
需求说明: 某企业信息中心计划使用IP地址17216.11.0用于虚拟网络测试,注册域名为xyz.net.cn.并将172.16.11.2作为主域名的服务器(DNS服务器)的IP地址,将172.16.11.3分配给虚拟网络测试的DHCP服务器,将172.16.11.4分配给虚拟网络测试的web服务器,将172.16.11.5分配给FTP服务器…...

CSS实现文字颜色渐变
直接上代码和效果图: <p class"linecolor">文字颜色渐变</p><style type"text/css">.linecolor{font-size: 30px;background-image:-webkit-linear-gradient(bottom,red,#fd8403,yellow);-webkit-background-clip:text;-web…...

《每天5分钟用Flask搭建一个管理系统》第4章:模板渲染
第4章:模板渲染 4.1 模板的概念和使用 模板是一种用于生成输出的方法,它允许您将Python代码和HTML标记混合在一起,从而创建动态网页。 示例代码:基本模板 <!-- templates/home.html --> <!DOCTYPE html> <html…...

逆向学习汇编篇:指令的操作
本节课在线学习视频(网盘地址,保存后即可免费观看): https://pan.quark.cn/s/660c759dea95 在逆向工程中,深入理解汇编语言的指令操作是至关重要的。汇编指令是计算机硬件与软件之间的桥梁,它们直…...
VB.net实战(VSTO):VSTOwpf体验框架打包教程
如果是考虑到Wps用户较多,就不建议采用侧边栏的形式 只是个体验框架,界面未作美化,office的用户可以用任意一种窗体,喜欢那个界面就写那个界面,wps的侧边栏只能弹出一部分,每次需要的手动拖动。 打包了案例…...

Jquery 获得Form下的所有text、checkbox等表单的值
Jquery使用表单我主要是想获得某一个表单下的所有text获得checkbox的值: 可以这样写: var parameter{}; $("input[typetext]",document.forms[0]).each(function(){ alert(this.name); }); 获得所有名为hobby的选中的checkbox的值和form2下的所有text的值 function s…...

stl之string
构造函数 void test1() {string s1;//不传参cout << s1 << endl;string s2("123456");cout << s2 << endl;string s3(s2);cout << s3 << endl;string s4(s2, 1, 5);cout << s4 << endl;string s5("123456&quo…...

Vue3学习笔记<->nginx部署vue项目
安装nginx vue项目通常部署到nginx上,所以先安装一个nginx。为了方便安装的是windows版nginx,解压就能用。 项目参考上一篇文章《Vue3学习笔记<->创建第一个vue项目》《Vue3学习笔记<->创建第一个vue项目》…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
