阅读笔记DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks
zi,t∈Rz_{i,t}\in \mathbb{R}zi,t∈R表示时间序列iii在ttt时刻的值。给一个连续时间段t∈[1,T]t\in [1, T]t∈[1,T],将其划分为context window[1,t0)[1,t_0)[1,t0)和prediction window[t0,T][t_0,T][t0,T]。用context window的时间序列预测prediction window的时间序列的目标分布是
P(zi,t0:T∣zi,1:t0−1,xi,1:T)P(\mathbf z_{i,t_0:T} | \mathbf z_{i,1:t_0-1}, \mathbf x_{i,1:T}) P(zi,t0:T∣zi,1:t0−1,xi,1:T)其中xi,t\mathbf x_{i,t}xi,t是协变量(covariate),也就是特征,可以是时间相关的,也可以是序列相关的,比如day-of-the-week、hour-of-the-day等。
作者用自回归(autoregressive)模型建模上面时间序列的概率:
QΘ(zi,t0:T∣zi,1:t0−1,xi,1:T)=Πt=t0TQΘ(zi,t∣zi,1:t−1,xi,1:T)=Πt=t0Tl(zi,t∣θ(hi,t,Θ))Q_\Theta(\mathbf z_{i,t_0:T} | \mathbf z_{i,1:t_0-1}, \mathbf x_{i,1:T})=\Pi_{t=t_0}^TQ_\Theta(z_{i,t} | \mathbf z_{i,1:t-1}, \mathbf x_{i,1:T}) = \Pi_{t=t_0}^T l(z_{i,t} | \theta(\mathbf h_{i,t}, \Theta)) QΘ(zi,t0:T∣zi,1:t0−1,xi,1:T)=Πt=t0TQΘ(zi,t∣zi,1:t−1,xi,1:T)=Πt=t0Tl(zi,t∣θ(hi,t,Θ))其中hi,t=h(hi,t−1,zi,t−1,xi,t,Θ)\mathbf h_{i,t} = h(\mathbf h_{i,t-1}, z_{i, t-1}, \mathbf x_{i,t}, \Theta)hi,t=h(hi,t−1,zi,t−1,xi,t,Θ)是RNN的隐含表示。likelihood l(zi,t∣θ(hi,t,Θ))l(z_{i,t} | \theta(\mathbf h_{i,t}, \Theta))l(zi,t∣θ(hi,t,Θ))是一个分布,参数由θ(hi,t,Θ)\theta(\mathbf h_{i,t}, \Theta)θ(hi,t,Θ)给出。

likelihood l(zi,t∣θ(hi,t,Θ))l(z_{i,t} | \theta(\mathbf h_{i,t}, \Theta))l(zi,t∣θ(hi,t,Θ))的参数由网络预测,例如分布的mean和variance。具体地,作者对实数值选择Gaussian likelihood,对正的计数值选择negative-binomial likelihood。
优化目标是最大化log-likelihood:
L=∑i=1N∑t=t0Tlogl(zi,t∣θ(hi,t))\mathcal L = \sum_{i=1}^N \sum_{t=t_0}^T \log l(z_{i,t} | \theta(\mathbf h_{i,t})) L=i=1∑Nt=t0∑Tlogl(zi,t∣θ(hi,t))因为模型没有隐变量,所以不需要inference,可以直接用梯度下降优化。需要优化的参数Θ\ThetaΘ包含RNN的参数,和计算分布参数的参数。
相关文章:

阅读笔记DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks
zi,t∈Rz_{i,t}\in \mathbb{R}zi,t∈R表示时间序列iii在ttt时刻的值。给一个连续时间段t∈[1,T]t\in [1, T]t∈[1,T],将其划分为context window[1,t0)[1,t_0)[1,t0)和prediction window[t0,T][t_0,T][t0,T]。用context window的时间序列预测prediction window…...

01.Java的安装
1.JDK&JREJDK : Java SE Development Kit--Java开发工具JRE : Java Runtime Environment--Java运行环境Java编程,需要安装JDK;如果仅仅是运行一款Java程序则只需要运行JREJava的安装包分为两类:一类是JRE--是一个独立的Java运行环境; 一类…...
【C语言深度剖析】关键字(全)
文章目录一.存储类型关键字前言补充1:内存思考:补充2:变量与内存的关系补充3:变量的分类补充4:存储类补充5:删除数据是怎么删除的?1.auto2.register3.static4.extern基本用法:基本功能5.typedef…...

English Learning - L2 语音作业打卡 双元音 [aʊ] [əʊ] Day15 2023.3.7 周二
English Learning - L2 语音作业打卡 双元音 [aʊ] [əʊ] Day15 2023.3.7 周二💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 /eɪ…...

记第一次面试的过程(C++)
说实话三月份上旬过得很充实,而且感觉蛮值,但还有不足的地方,今晚特地看完资料分析来复盘复盘。 时间还要回到3.2中午13.35(别问我为什么那么准确,刚刚掏手机看的),我正在吃着饭看着王者荣耀的直…...
06 电力电子仿真 MATLAB/Simulink
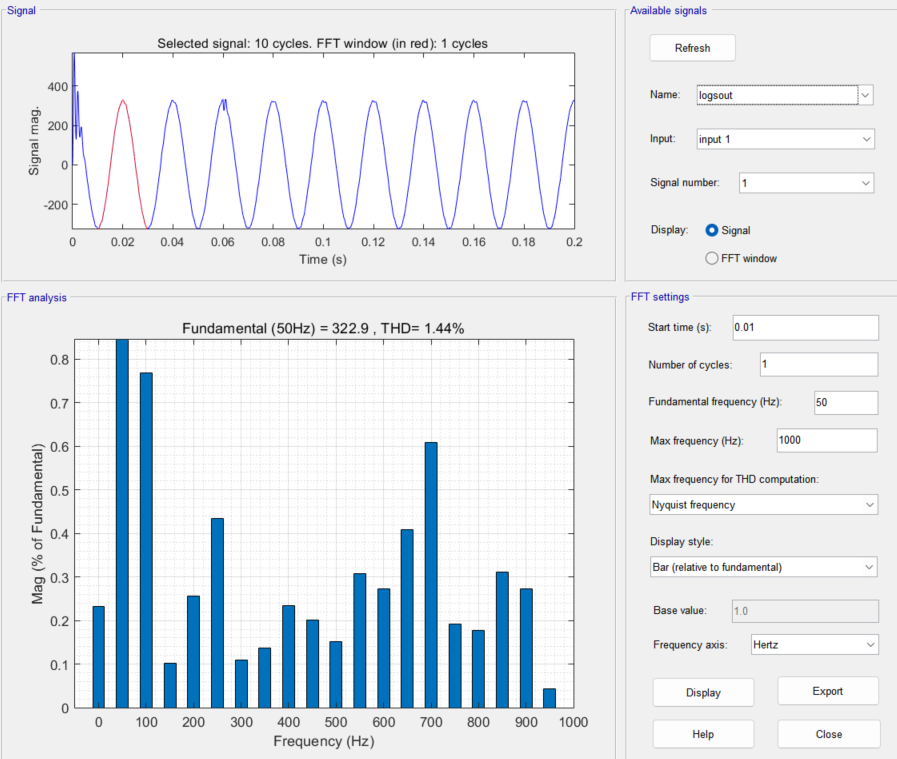
文章目录01 单相半波整流电路02 单相全波整流电路(子系统封装模块)03 三相桥式整流电路(三相模块与示波器使用)04 相控与斩控交交调压(THD计算)05 Buck电路(PWM实现与闭环反馈)06 单…...

搞懂面向对象这五大概念,才算真正跨过初学者到开发者的“分水岭“
文章目录前言一、对象二、类三、面向对象程序设计的特点1. 封装2. 继承3. 多态前言 面向对象程序设计是在面向过程程序设计的基础上发展而来的,它比面向过程编程具有更强的灵活性和扩展性。面向对象程序设计也是一个程序员发展的 “分水岭”,很多的初学者…...

基于DelayQueue实现的延时队列
基于java中延时队列的实现该文章,我们这次主要是来实现基于DelayQueue实现的延时队列。 使用DelayQueue实现的延时队列的步骤: 定义一个继承了Delayed的类,定义其中的属性,并重写compareTo和getDelay两个方法创建一个Delayqueue…...

MATLAB实现层次分析法AHP及案例分析
层次分析法(Analytic Hierarchy Process, AHP) 1 模型背景 美国运筹学家匹兹堡大学教授Saaty在20世纪70年代初提出的一种层次权重决策分析方法。 层次分析法(Analytic Hierarchy Process, AHP)是一种定性和定量分析相结合的决策分析方法。 特点:用较少的定量信息使决策的…...

Vue 3.0 TypeScript支持
Vue CLI 提供内置的 TypeScript 工具支持。 #NPM 包中的官方声明 随着应用的增长,静态类型系统可以帮助防止许多潜在的运行时错误,这就是为什么 Vue 3 是用 TypeScript 编写的。这意味着在 Vue 中使用 TypeScript 不需要任何其他工具——它具有一流的公…...
STM8S系列基于IAR标准外设printf输出demo
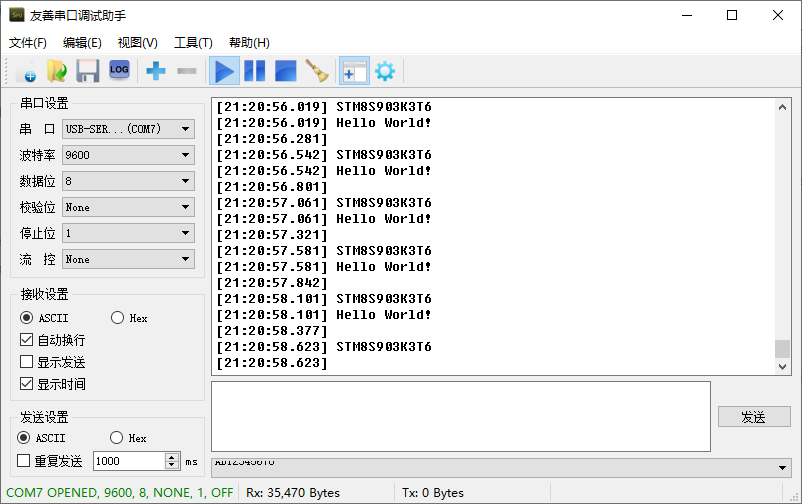
STM8S系列基于IAR标准外设printf输出demo📌STM8S/A标准外设库(库版本V2.3.1)📍官网标准外设库:https://www.st.com/zh/embedded-software/stsw-stm8069.html ⛳注意事项 🚩在内存空间比较有限的情况下&am…...
PMP项目管理项目质量管理
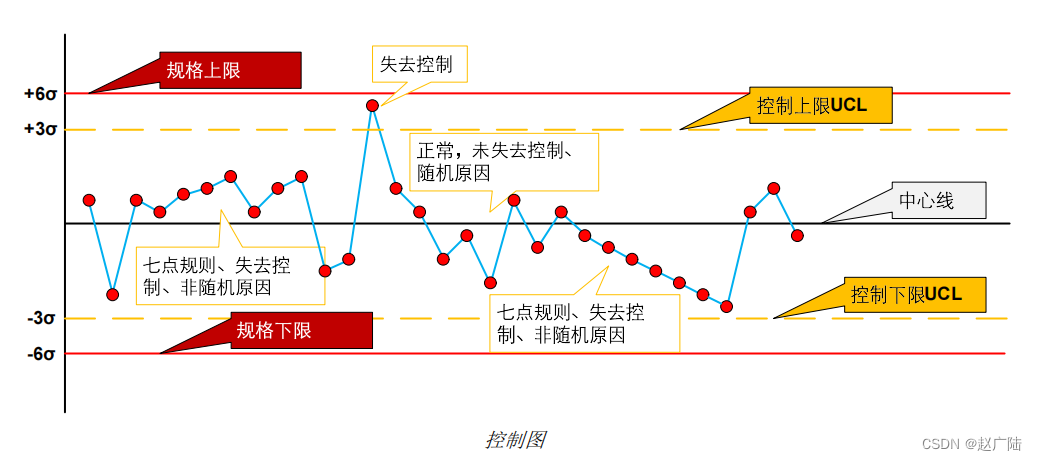
目录1 项目质量管理概述2 规划质量管理3 管理质量4 控制质量1 项目质量管理概述 项目质量管理包括把组织的质量政策应用于规则、管理、控制项目和产品质量要求,以满足相关方目标的各个过程。项目质量管理还将以组织的名义支持过程的持续改进活动。 核心概念 质量是…...

前缀和总结
前缀和是一个常用的算法技巧,通常用于求解数组或序列的区间和。 具体来说,假设有一个长度为n的数组a,我们可以预处理出一个长度为n+1的前缀和数组s,其中s[i]表示原数组a前i个元素的和,即: s[i] = a[0] + a[1] + ... + a[i-1] 这样一来,对于任意的区间[l, r],我们可以…...

0109二分图-无向图-数据结构和算法(Java)
文章目录1 概念2 API3 分析和实现4 测试5 总结后记1 概念 二分图是一种能将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。 2 API public classBipartiteBipartite(Graph G)预处理函数public booleanisBipartitle()是否是二分图pub…...
)
计算机网络题库---选择题刷题训练(100多道精品)
第一章 概述 1.下列四项内容中,不属于Internet(因特网)基本功能是___D_____。 A.电子邮件 B.文件传输 C.远程登录 D.实时监测控制 2.Internet是建立在____C_____协议集上的国际互联网络。 A.IPX B.NetBEUI C.TCP/IP …...

16、字符串生成器
目录 (1)append()方法 (2)insert(int offset, arg)方法 (3)delete(int start , int end)方法 创建成功的字符串对象,其长度是固定的,内容不能被改变和编译。虽然使用“”可以达到…...

docker基本命令-容器
容器 基本概念 镜像(Image)和容器(Container)的关系,就像是面向对象程序设计中的 类 和 实例 一样,镜像是静态的定义,容器是镜像运行时的实体。容器可以被创建、启动、停止、删除、暂停等。 容…...
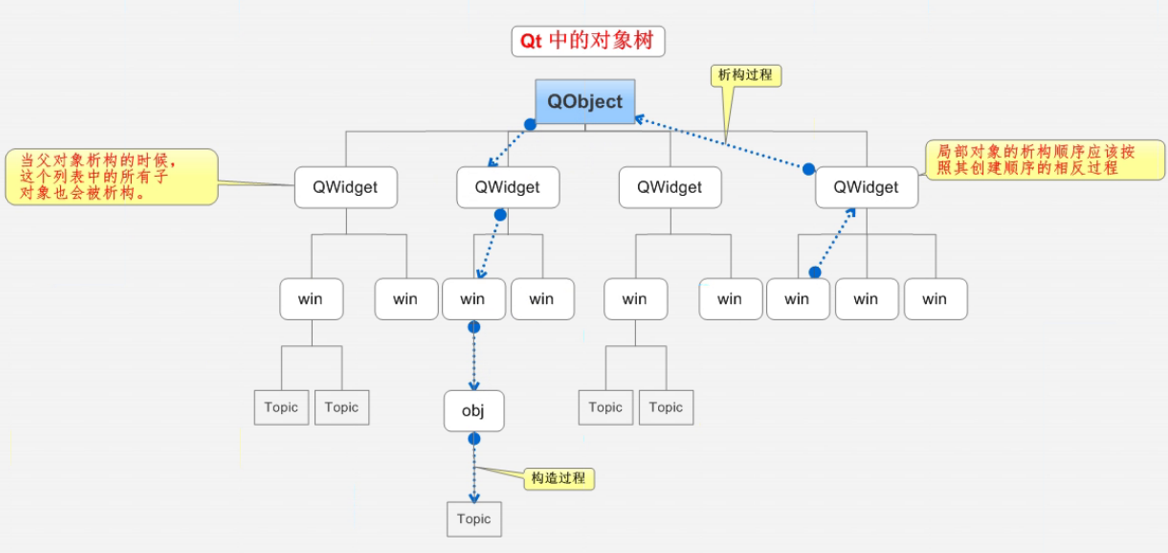
QT入门基础(一)
文章目录零.Qt背景1.什么是Qt2.Qt的发展史3.Qt的优势4.Qt应用一.第一个Qt程序0.项目创建1.main函数文件2.类头文件3.pro文件4.qt命名规范二.Qt按钮1.按钮创建和父子关系2.按钮常用api3.Qt窗口坐标体系4.对象树模型零.Qt背景 1.什么是Qt Qt是一个跨平台的C图形用户界面应用程序…...
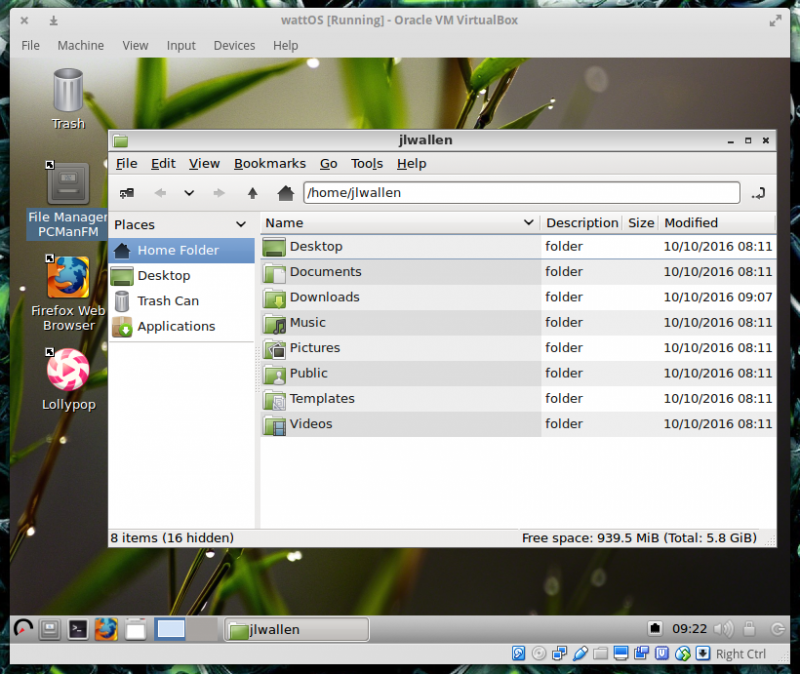
WattOS:一个稳又快的轻量级 Linux 发行版
导读Linux 领域里的每个人不是听说过就是使用过某个轻量级的 Linux 发行版。大家都知道我们不断追求的是:占用内存少,配置资源要求低,包含一个轻量级的桌面环境(或者窗口管理器),并且提供和其他发行版相似的…...

Java调用Python脚本:轻松实现两种语言的互操作性
Java和Python都是非常流行的编程语言,它们都有自己的优点,但也有自己的局限性。在编写应用程序时,我们可能需要使用两种语言来共同完成一项任务。在这种情况下,Java需要调用Python脚本来解决某些问题,同时利用Java和Py…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
