【强化学习】第02期:动态规划方法
笔者近期上了国科大周晓飞老师《强化学习及其应用》课程,计划整理一个强化学习系列笔记。笔记中所引用的内容部分出自周老师的课程PPT。笔记中如有不到之处,敬请批评指正。
文章目录
- 2.1 动态规划:策略收敛法/策略迭代法
- 2.2 动态规划:值迭代法
总的来说,DP方法就是在已知bellman方程的环境参数(回报R和转移概率P)的情况下,求取最优策略 u ∗ u^* u∗和最优值 v ∗ v^* v∗。
2.1 动态规划:策略收敛法/策略迭代法
总体思路:算V --> 算Q --> 策略改进 (不断重复)
初始化最优策略 u,
Step1 策略评估: 确定当前策略 𝜋 的值函数 V π V^π Vπ,可通过下面的式子求解。
Step2 计算动作值函数Q: 使用值函数 V π V^π Vπ来计算每个状态-动作对的动作值函数 Q π ( s , a ) Q^π(s,a) Qπ(s,a)。这一步是为了计算在当前策略 𝜋 下,每个状态-动作对的期望回报。
Step3 策略改进: 对每个状态 𝑠 选择能使 Q π ( s , a ) Q^π(s,a) Qπ(s,a)最大的动作𝑎,从而形成新的策略 𝜋′。这一步是为了更新策略,使其更接近最优策略。
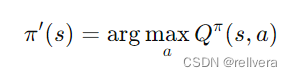
Step4: goto Step1, 直到最优策略u不变。
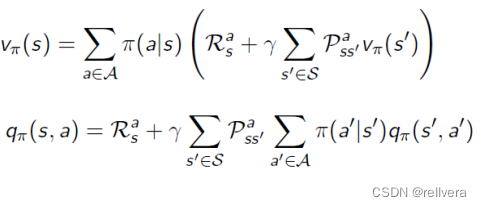
2.2 动态规划:值迭代法
值迭代(Value Iteration)是一种用于求解马尔可夫决策过程(MDP)的经典动态规划算法。它通过迭代地更新值函数,逐步逼近最优值函数 V ∗ V^* V∗ ,最终得到最优策略 π ∗ π^* π∗。
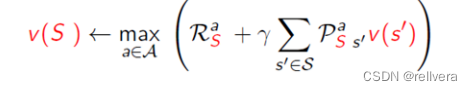
值迭代一般分为这几个步骤:
step1 初始化:设定初始值函数 V ( s ) V(s) V(s)为零或其他任意值。
step2 迭代更新:对于每个状态 𝑠 ,根据当前值函数 V k V_k Vk计算新的值函数 V k + 1 V_{k+1} Vk+1。这个更新过程通过遍历所有状态和所有可能的动作,计算在每个状态下采取每个动作所能获得的期望累计奖励,并选择其中的最大值作为新的值函数值。
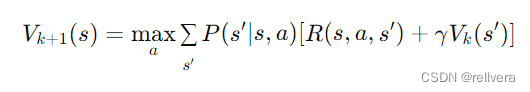
step3 收敛判定:当值函数的变化小于某个预设的阈值 𝜃 时,认为值函数已经收敛,可以停止迭代。
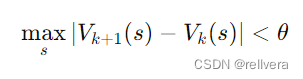
step4 策略提取:在值函数收敛后,通过值函数 V ∗ V^* V∗ 提取最优策略 π ∗ π^* π∗:
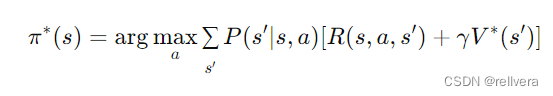
关于值迭代,也有很多处理技巧,这里简单介绍三种。
(1)In-place Dynamic Programming
在标准的值迭代过程中,我们通常会维护两个值函数,一个用于保存当前迭代的结果,另一个用于保存上一次迭代的结果。而在 In-place Dynamic Programming 中,我们只使用一个值函数数组,在每次更新时直接覆盖旧的值。
特点:只需要一个数组来存储值函数,减少了内存消耗。
(2)Prioritized Sweeping
是一种加速值迭代的方法,通过优先更新那些对值函数变化影响较大的状态,从而提高收敛速度。
(3)Real-time Dynamic Programming (RTDP)
是一种在实际运行过程中更新值函数的方法,适用于在线学习。
相关文章:
【强化学习】第02期:动态规划方法
笔者近期上了国科大周晓飞老师《强化学习及其应用》课程,计划整理一个强化学习系列笔记。笔记中所引用的内容部分出自周老师的课程PPT。笔记中如有不到之处,敬请批评指正。 文章目录 2.1 动态规划:策略收敛法/策略迭代法2.2 动态规划…...
)
安全技术和防火墙(二)
接上一节 备份和还原 iptables-save > /opt/iptables.bak iptables-restore < /opt/iptables.bak snat和dnat snat源地址转换 内网到外网 内网ip转换成可以访问外网的ip 内网的多个主机可以只有一个有效的公网ip地址访问外部网络 dnat 目的地址转发 外部用户&#…...
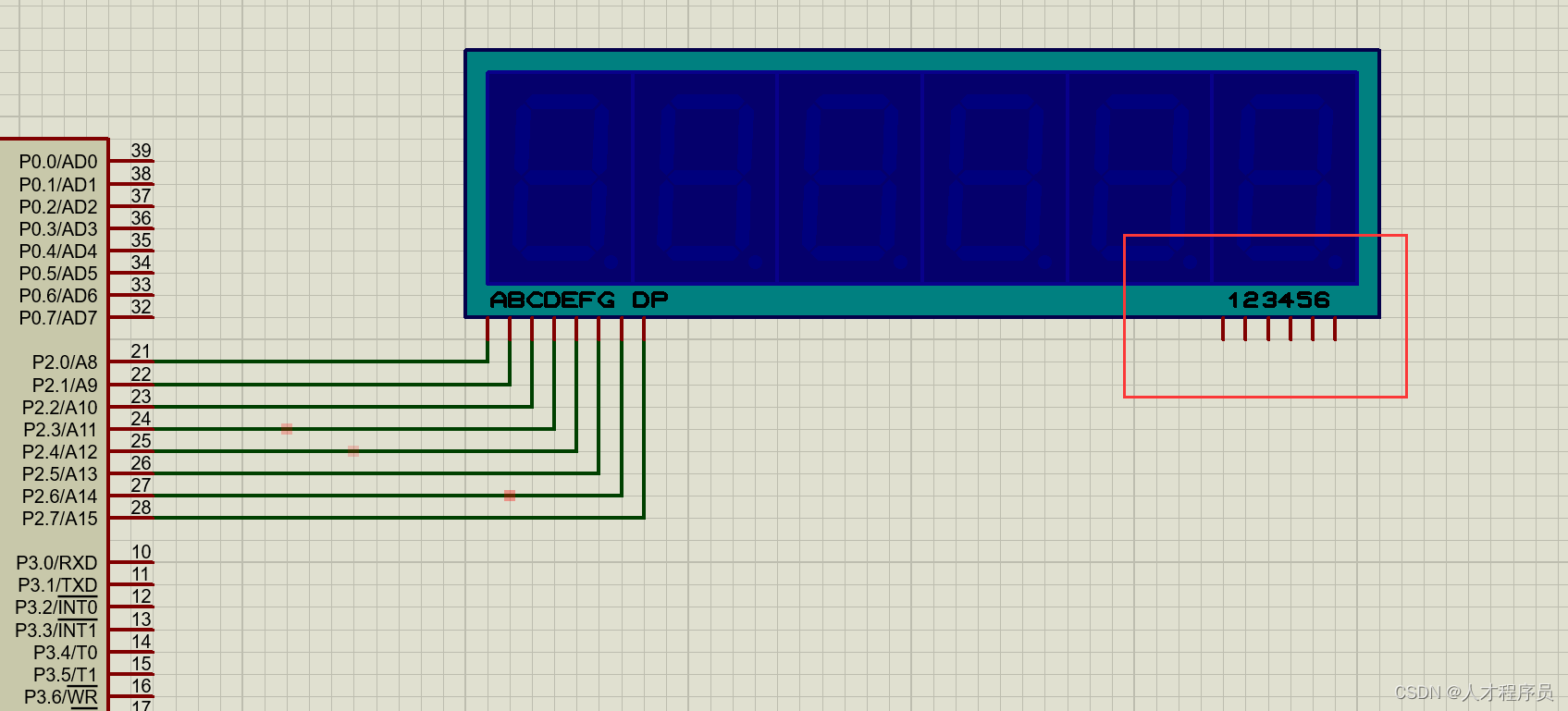
【51单片机入门】数码管原理
文章目录 前言共阴极与共阳极数码管多个数码管显示原理 总结 前言 在我们的日常生活中,数码管被广泛应用于各种电子设备中,如电子表、计时器、电子钟等。数码管的主要功能是显示数字和一些特殊字符。在这篇文章中,我们将探讨数码管的工作原理…...

三星DRAM、NAND,“又双叒叕”带头涨价了
据韩国媒体《每日经济新闻》报道,三星电子计划在第三季度上调服务器DRAM和企业级NAND闪存的价格,涨幅预计在15%-20%,主要受人工智能(AI)需求激增的推动。这一举措有望提振公司下半年业绩。 据《经济日报》报道援引业内消息,由于厂…...

星戈瑞FITC-PEG2000-Biotin的生物相容性
生物相容性是指材料与生物体之间相互作用时,材料对生物体无毒、无刺激,且能够被生物体接受并正常发挥其功能的特性。 FITC-PEG2000-Biotin作为一种荧光标记试剂,在细胞成像、药物传递和生物标志物检测等领域具有诸多应用前景。 FITC-PEG2000…...

数据资产管理的艺术:构建智能化、精细化的数据资产管理体系,从数据整合、分析到决策支持,为企业提供一站式的数据资产解决方案,助力企业把握数字时代的新机遇
一、引言 在数字化浪潮席卷全球的今天,数据已经成为企业最重要的资产之一。如何高效、安全地管理这些海量数据,从中提取有价值的信息,并将其转化为决策支持,是每个企业都必须面对的挑战。本文将探讨数据资产管理的艺术࿰…...

基于Java微信小程序校园自助打印系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 🌟文末获取源码数据库🌟感兴趣的可以先收藏起来,还…...

股票复盘思路
股票复盘是一个回顾和分析市场及个人交易决策的过程,旨在从过去的表现中学习并优化未来的投资策略。以下是一些基本的股票复盘步骤和关注点: 市场概况回顾: 观察并记录每日市场的整体表现,包括大盘指数涨跌、成交量变化。统计涨停和跌停个股的数量,了解市场情绪和活跃度。…...
摄像机)
OpenGL系列(六)摄像机
在 OpenGL系列(六)变换 中,一个目标物体经过模型矩阵、观察矩阵和投影矩阵的变换才能正常显示出来,其中模型矩阵主要针对目标物体,它会影响物体的位姿。观察矩阵和投影矩阵主要针对观察者而已,这两个变换决…...

一个端口配置两个vue和后端服务,nginx以及前后端服务怎么配?
nginx配置重点看server中的内容: worker_processes 8; pid /usr/local/nginx/logs/nginx.pid;events {# 此为 Linux 系统特为处理大批量文件描述符而作改进的 poll 事件模型use epoll;worker_connections 512; # 工作进程的最大连接数量# 允许同时接受多个网络连…...

295. 数据流的中位数
class MedianFinder {Queue<Integer> A,B;public MedianFinder() {A new PriorityQueue<>();//小根堆存储后半部分B new PriorityQueue<>((x,y)->(y-x));//大根堆存储前半部分}public void addNum(int num) {if(A.size()0 && B.size()0){B.add(…...
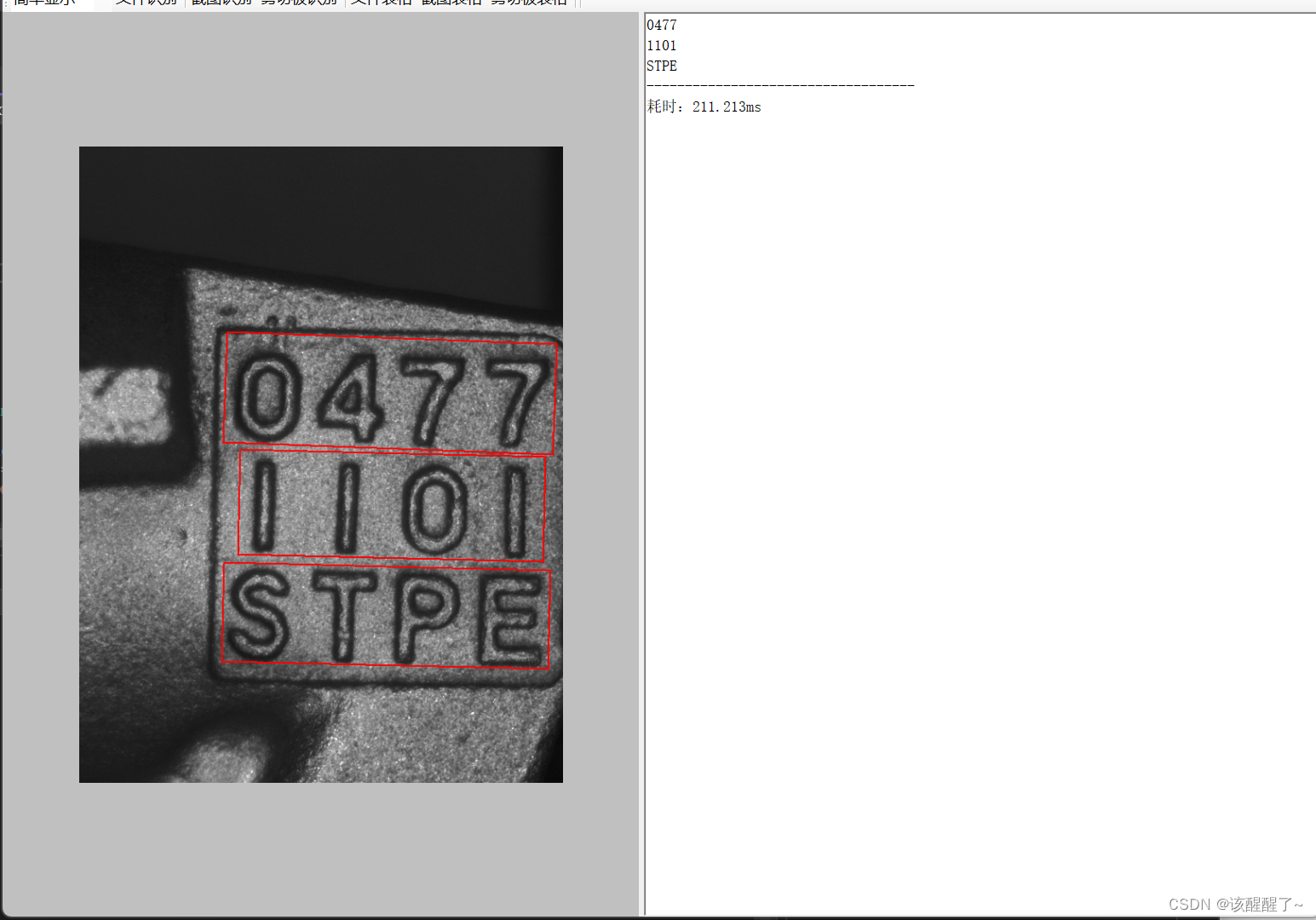
OCR训练和C#部署英文字符训练
PaddleOCR是一个基于飞桨开发的OCR(Optical Character Recognition,光学字符识别)系统。其技术体系包括文字检测、文字识别、文本方向检测和图像处理等模块。以下是其优点: 高精度:PaddleOCR采用深度学习算法进行训练…...
webpack【实用教程】
基础配置 配置的拆分和合并 通常 webpack 的配置文件会有3个 webpack.common.js 公共配置(会被另外两个配置文件导入并合并)webpack.dev.js 开发环境的配置webpack.prod.js 生产环境的配置 开发环境的本地服务 在 webpack.dev.js 中配置 devServer:…...

如何使用C++进行文件读写操作
在C中,我们可以使用标准库中的 <fstream>(文件流)来进行文件的读写操作。以下是一些基本的文件读写操作的示例。 读取文件 cpp复制代码 #include <fstream> #include <iostream> #include <string> int main() { s…...

Tensorflow Lite移动平台编译
Android平台编译 如果不做定制化操作,我们不需要自己编译TensorFlow Lite Android库。我们可以直接使用位于MavenCentral的TensorFlow Lite AAR。但是在某些情况下,我们需要本地编译TensorFlow Lite。例如,您可能正在构建一个包含operations selected from TensorFlow的自定…...
)
2024年6月24日-6月30日(ue5肉鸽视频p16-p25)
试过重点放在独立游戏上,有个indienova独立游戏团队是全职的,由于他们干了几个月,节奏暂时跟不上,紧张焦虑了。五一时也有点自暴自弃了,实在没必要,按照自己的节奏走即可。精力和时间也有限,放在…...

LeetCode.面试题17.24.最大子矩阵详解
问题描述 给定一个正整数、负整数和 0 组成的 N M 矩阵,编写代码找出元素总和最大的子矩阵。 返回一个数组 [r1, c1, r2, c2],其中 r1, c1 分别代表子矩阵左上角的行号和列号,r2, c2 分别代表右下角的行号和列号。若有多个满足条件的子矩阵…...

云动态摘要 2024-06-28
给您带来云厂商的最新动态,最新产品资讯和最新优惠更新。 最新优惠与活动 [新客专享]WeData 限时特惠 腾讯云 2024-06-21 数据分类分级管理,构建数据安全屏障 ,仅需9.9元! 云服务器ECS试用产品续用 阿里云 2024-04-14 云服务器…...

六、资产安全—信息分级资产管理与隐私保护(CISSP)
目录 1.信息分级 2.信息分级方法 3.责任的层级 4.资产管理 5.隐私数据管理角色 6.数据安全控制 7.数据保护方案 8.使用安全基线 六、资产安全—数据管理(CISSP): 五、身份与访问管理—身份管理和访问控制管理(CISSP): 1.信息分级 信息分级举列: 2.信息分级方…...

香港服务器托管对外贸行业必要性和优势
在当今全球化的经济环境下,外贸企业面临着前所未有的机遇与挑战。其中,服务器托管的选择对于外贸企业的运营效率和市场拓展具有举足轻重的作用。香港服务器,凭借其独特的地理位置、优质的网络环境和卓越的服务性能,一直是外贸企业…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
