LeetCode.面试题17.24.最大子矩阵详解
问题描述
给定一个正整数、负整数和 0 组成的 N × M 矩阵,编写代码找出元素总和最大的子矩阵。
返回一个数组 [r1, c1, r2, c2],其中 r1, c1 分别代表子矩阵左上角的行号和列号,r2, c2 分别代表右下角的行号和列号。若有多个满足条件的子矩阵,返回任意一个均可。
解题思路
1. 基础概念:Kadane算法
首先,我们需要了解Kadane算法,这是一种用于在一维数组中找到最大子数组和的算法。给定一个数组,该算法可以找到一个连续子数组,其元素之和最大,并且能返回这个最大和。
2. 将问题从二维转化为一维
要在二维矩阵中寻找最大子矩阵和,我们可以通过固定列的起始和结束点来将问题简化为一维问题:
- 固定列界限:选择两个列的索引,left和right,使得这两个索引之间的所有列都被包含在内。
- 累加行元素:对于每个行,计算从left列到right列的元素和,得到一个新的“行和数组”。例如,如果left和right都是1(即第二列),那么行和数组中的每个元素就是原矩阵该行第二列的元素。
3. 应用Kadane算法到行和数组
对每一个固定的列对(left和right),我们都得到了一个行和数组。接下来:
- 使用Kadane算法:将Kadane算法应用于行和数组,找出这个数组中的最大子数组和以及对应的起始行和结束行。
- 记录最大和及其位置:如果这次的最大子数组和大于之前记录的最大值,更新最大值和相应的行和列索引。这些索引就确定了最大子矩阵的边界。
4. 处理所有可能的列对
- 从第一列开始,逐一将每列作为起始列,然后对每个可能的结束列重复上述过程。
- 这意味着,我们首先固定起始列,然后让结束列从起始列开始向右延伸至矩阵的最后一列,对每种情况都计算行和数组,然后应用Kadane算法。
5. 输出最终结果
在所有列对组合被考虑之后,全局记录的最大值及其对应的子矩阵边界就是我们的答案。这些信息可以用来标识出具有最大和的子矩阵。
代码实现
class Solution {
public:vector<int> getMaxMatrix(vector<vector<int>>& matrix) {int maxSum = INT_MIN;vector<int> result(4); // 存放最终结果,[r1, c1, r2, c2]int rows = matrix.size(), cols = matrix[0].size();// 遍历所有列的组合for (int left = 0; left < cols; ++left) {vector<int> rowSum(rows, 0); // 初始化行和数组for (int right = left; right < cols; ++right) {// 计算从left到right列的行和for (int i = 0; i < rows; ++i) {rowSum[i] += matrix[i][right];}// 应用Kadane算法找到最大的子数组和及其索引int currentMax = INT_MIN, tempSum = 0;int rowStart = 0, tempRowStart = 0, rowEnd = 0;for (int i = 0; i < rows; ++i) {if (tempSum <= 0) {tempSum = rowSum[i];tempRowStart = i;} else {tempSum += rowSum[i];}if (tempSum > currentMax) {currentMax = tempSum;rowStart = tempRowStart;rowEnd = i;}}// 更新全局最大和及对应的子矩阵坐标if (currentMax > maxSum) {maxSum = currentMax;result = {rowStart, left, rowEnd, right};}}}return result;}
};相关文章:

LeetCode.面试题17.24.最大子矩阵详解
问题描述 给定一个正整数、负整数和 0 组成的 N M 矩阵,编写代码找出元素总和最大的子矩阵。 返回一个数组 [r1, c1, r2, c2],其中 r1, c1 分别代表子矩阵左上角的行号和列号,r2, c2 分别代表右下角的行号和列号。若有多个满足条件的子矩阵…...

云动态摘要 2024-06-28
给您带来云厂商的最新动态,最新产品资讯和最新优惠更新。 最新优惠与活动 [新客专享]WeData 限时特惠 腾讯云 2024-06-21 数据分类分级管理,构建数据安全屏障 ,仅需9.9元! 云服务器ECS试用产品续用 阿里云 2024-04-14 云服务器…...

六、资产安全—信息分级资产管理与隐私保护(CISSP)
目录 1.信息分级 2.信息分级方法 3.责任的层级 4.资产管理 5.隐私数据管理角色 6.数据安全控制 7.数据保护方案 8.使用安全基线 六、资产安全—数据管理(CISSP): 五、身份与访问管理—身份管理和访问控制管理(CISSP): 1.信息分级 信息分级举列: 2.信息分级方…...

香港服务器托管对外贸行业必要性和优势
在当今全球化的经济环境下,外贸企业面临着前所未有的机遇与挑战。其中,服务器托管的选择对于外贸企业的运营效率和市场拓展具有举足轻重的作用。香港服务器,凭借其独特的地理位置、优质的网络环境和卓越的服务性能,一直是外贸企业…...

Vue Router 导航守卫,多次执行的解决方案
Vue Router 是 Vue.js 官方提供的路由器,它用于处理单页应用(SPA)中的路由导航。在 Vue Router 中,导航守卫是非常重要的功能,它可以在路由跳转之前或之后执行一些特定的操作。但是,如果你不小心,导航守卫可能会多次执行,这可能会导致一些问题。本文将介绍如何避免导航…...

SpringBoot集成道历(实现道历日期查询)
官网地址:官网地址https://6tail.cn/calendar/api.html 1、导入依赖 <dependency><groupId>cn.6tail</groupId><artifactId>lunar</artifactId><version>1.3.9</version></dependency><dependency><group…...
面对.rmallox勒索病毒:如何有效防范及应对
引言: 在当今数字化社会,网络安全问题日益严重,勒索病毒成为企业和个人不可忽视的威胁之一。最近出现的.rmallox勒索病毒更是给全球各地的用户带来了严重的数据安全问题。本文将探讨.rmallox勒索病毒的特点、感染方式及应对策略,…...
嘉立创学习
1.两个设置,一般用左边那个 2.焊盘分类 基本焊盘 热风盘:也叫花焊盘(负片) 隔离焊盘:外面那圈黑色,用作隔离(负片) 钢网层:(锡膏) 阻焊层&…...

ECharts 响应式设计
ECharts 响应式设计 ECharts 是一个由百度开源的,基于 JavaScript 的可视化库,它提供了一系列丰富的图表类型和灵活的配置选项,使得数据可视化变得简单而高效。在当今数据驱动的世界中,ECharts 已经成为许多开发者和设计师的首选工具,用于创建交互式和视觉吸引力强的图表…...

基于java语言+springboot技术架构开发的 互联网智能3D导诊系统源码支持微信小程序、APP 医院AI智能导诊系统源码
基于java语言springboot技术架构开发的 互联网智能3D导诊系统源码支持微信小程序、APP 医院AI智能导诊系统源码 一、智慧导诊系统开发原理 导诊系统从原理上大致可分为基于规则模板和基于数据模型两类。 1、基于规则推理的方法通过人工建立症状、疾病和科室之间的对应规则实现…...
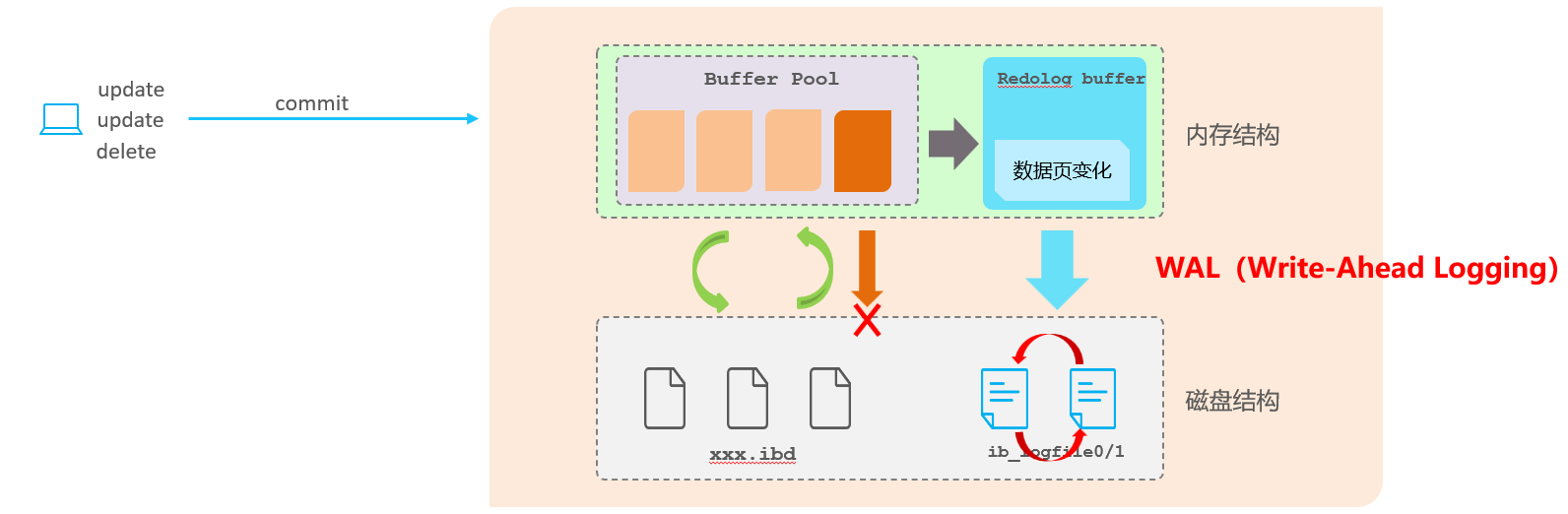
MySQL事务——Java全栈知识(31)
1、事务的特性 原子性(Atomicity):事务是不可分割的最小操作单元,要么全部成功,要么全部失败。 一致性(Consistency):事务完成时,必须使所有的数据都保持一致状态。 隔离…...

2毛钱不到的2A同步降压DCDC电压6V频率1.5MHz电感2.2uH封装SOT23-5芯片MT3520B
前言 2A,2.3V-6V输入,1.5MHz 同步降压转换器,批量价格约0.18元 MT3520B 封装SOT23-5 丝印AS20B5 特征 高效率:高达 96% 1.5MHz恒定频率操作 2A 输出电流 无需肖特基二极管 2.3V至6V输入电压范围 输出电压低至 0.6V PFM 模式可在…...
Ubuntu安装、更新和删除软件
Ubuntu安装、更新和删除软件 问题命令行直接安装、更新和删除软件命令行直接安装软件命令行直接更新软件命令行直接删除软件 手动下载后命令行安装、更新和删除软件手动下载后命令行安装软件手动下载后命令行更新软件手动下载后命令行删除软件 手动下载后在桌面环境下安装、更新…...

消息队列kafka中间件详解:案例解析(第10天)
系列文章目录 1- 消息队列(熟悉)2- Kafka的基本介绍(掌握架构,其他了解)3- Kafka的相关使用(掌握kafka常用shell命令)4- Kafka的Python API的操作(熟悉) 文章目录 系列文…...
Linux高级编程——线程
pthread 线程 概念 :线程是轻量级进程,一般是一个进程中的多个任务。 进程是系统中最小的资源分配单位. 线程是系统中最小的执行单位。 优点: 比多进程节省资源,可以共享变量 进程会占用&am…...

技术学习的奥秘与乐趣
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 在当今快速发展的科技时代,学习技术已经成为了许多人追求的重要目标之一。无论是为了个人发展&#…...

创新前沿:Web3如何颠覆传统计算机模式
随着Web3技术的快速发展,传统的计算机模式正面临着前所未有的挑战和改变。本文将深入探讨Web3技术的定义、原理以及它如何颠覆传统计算机模式,以及对全球科技发展的潜在影响。 1. 引言:Web3技术的兴起与背景 Web3不仅仅是技术创新的一种&…...

一文弄懂梯度下降算法
1、引言 在上一篇文章中,我们介绍了如何使用线性回归和成本损失函数为房价数据找到最拟合的线。不过,我们也看到,测试多个截距值可能既繁琐又低效。在本文中,我们将深入探讨梯度下降算法,这是一种更加强大的技术&…...

确认偏差:金融市场交易中的隐形障碍
确认偏差,作为一种深刻影响交易员决策与表现的心理现象,其核心在于个体倾向于寻求与既有信念相符的信息,而自动过滤或轻视与之相悖的资讯。这种认知偏见严重扭曲了交易者的决策过程,导致他们过分依赖符合既有观念的数据࿰…...

Linux系统之部署linkding书签管理器
Linux系统之部署linkding书签管理器 一、linkding介绍1.1 linkding简介1.2 linkding特点二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍三、检查本地环境3.1 检查本地操作系统版本3.2 检查系统内核版本四、部署Node.js 环境4.1 下载Node.js安装包4.2 解压Node.js安装包4.3 …...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
