信息学奥赛初赛天天练-38-CSP-J2021阅读程序-约数个数、约数和、埃氏筛法、欧拉筛法筛素数应用
PDF文档公众号回复关键字:20240628

2021 CSP-J 阅读程序3
1阅读程序(判断题1.5分 选择题3分 共计40分 )
01 #include<stdio.h>
02 using namespace std;
03
04 #define n 100000
05 #define N n+1
06
07 int m;
08 int a[N],b[N],c[N],d[N];
09 int f[N],g[N];
10
11 void init()
12 {
13 f[1]=g[1]=1;
14 for(int i=2;i<=n;i++){
15 if(!a[i]){
16 b[m++]=i;
17 c[i]=1,f[i]=2;
18 d[i]=1,g[i]=i+1;
19 }
20 for(int j=0;j<m&&b[j]*i<=n;j++){
21 int k=b[j];
22 a[i*k]=1;
23 if(i%k==0){
24 c[i*k]=c[i]+1;
25 f[i*k]=f[i]/c[i*k]*(c[i*k]+1);
26 d[i*k]=d[i];
27 g[i*k]=g[i]*k+d[i];
28 break;
29 }
30 else{
31 c[i*k]=1;
32 f[i*k]=2*f[i];
33 d[i*k]=g[i];
34 g[i*k]=g[i]*(k+1);
35 }
36 }
37 }
38 }
39
40 int main()
41 {
42 init();
43
44 int x;
45 scanf("%d",&x);
46 printf("%d %d\n",f[x],g[x]);
47 return 0;
48 }
假设输入的x是不超过1000的自然数,完成下面的判断题和单选题
判断题
28.若输入不为"1",把第13删去不会影响输出的结果( )
29.(2分) 第25行的"f[i]/c[i*k]"可能存在的无法整除而向下取取整的情况( )
30.(2分)在执行完init()后,f数组不是单调递增的,但g数组是单调递增的( )
单选题
31.init 函数的时间复杂度为( )
A. O(n)
B. O(nlogn)
C. O(n sqrt(n))
D. O(n^2)
32.在执行完init()后,f[1],f[2],f[3]… f[100]中有( )个等于2.
A. 23
B. 24
C. 25
D. 26
33.(4分)当输入为"1000"时,输出为( )
A. “15 1340”
B. “15 2340”
C. “16 2340”
D. “16 1340”
2 相关知识点
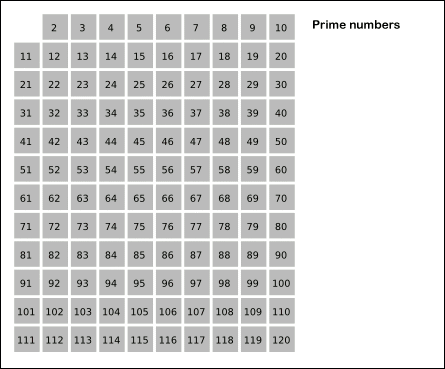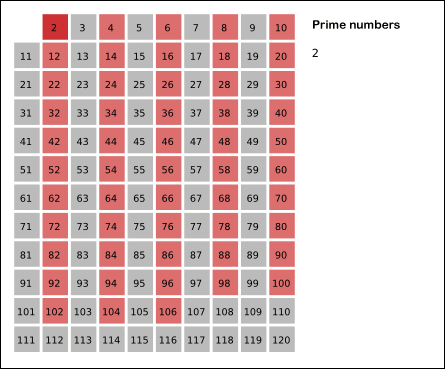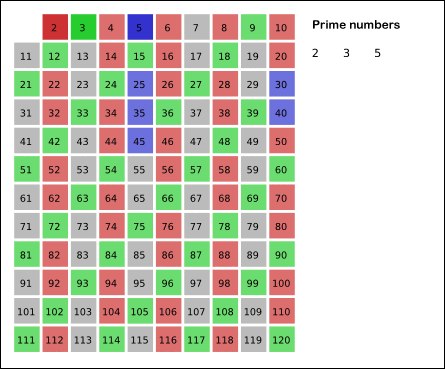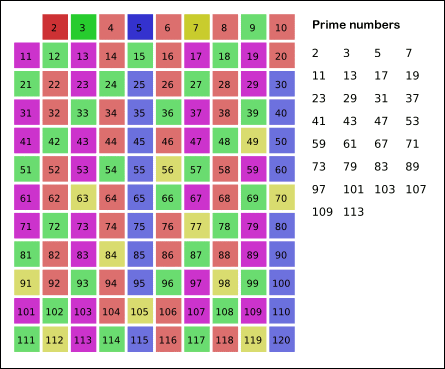
埃式筛法
如果一个数是素数,那么它的倍数一定不是素数。我们要找n以内的所有素数,那么把n以内的合数全部筛掉,剩下的就是素数了
时间复杂度
O(n * log (log n) )
欧拉筛法
将合数分解为一个最小质数乘以另一个数的形式,即 合数 = 最小质数 * 自然数,然后通过最小质数来判断当前数是否被标记过
时间复杂度
O(n)
3 思路分析
分析
本程序通过欧拉筛求约数个数及其约数和
使用到的对应数组
标记a数组,对合数进行标记,未标记的则是质数
质数表b数组,从小到大知道质数写到b数组
约数个数f数组,记录一个数对应的约数的个数
在填入约数个数f数组时,使用到最小质因数个数c数组
在填入约数和g数组时,使用到约数和对应的连乘积除第1项外的其他连乘积d数组
约数和g数组,记录一个数对应的约数之和
08 int a[N],b[N],c[N],d[N];
09 int f[N],g[N];
假设输入的x是不超过1000的自然数,完成下面的判断题和单选题
判断题
28.若输入不为"1",把第13删去不会影响输出的结果( T )
分析
13行程序计算并未使用,只对f[1],g[1]输出有影响,如果不输出f[1],g[1],不会影响输出
所以输入不为"1",删除不影响输出结果
29.(2分) 第25行的"f[i]/c[i*k]"可能存在的无法整除而向下取取整的情况( F )
分析
c[i]表示i的最小质因数个数
f[i]表示i的约数个数,计算公式如下H = p1^a1 * p2^a2 ....pn^an 其中 pi都是质数,ai是幂次,p1是最小的质数
约数的个数f[i]=(a1+1)*(a2+1)*...(an+1)
其中a1是最小质因数个数
c[i]表示i的最小质因数个数=a1
满足条件i%k==0
c[i*k]=相当于最小质数+1=a1+1
a1+1是f[i]的因子,所以f[i]/c[i*k]不会存在无法整除的情况
所以错误
30.(2分)在执行完init()后,f数组不是单调递增的,但g数组是单调递增的( F )
分析
f数组是约数个数,合数个数多,质数个数少,3 4 5 对应约数个数分别是2 3 2 看,并不是单调递增的
g数组是约数和,3 4 5 对应约数和分别是4 7 6 看,并不是单调递增的
单选题
31.init 函数的时间复杂度为( A )
A. O(n)
B. O(nlogn)
C. O(n sqrt(n))
D. O(n^2)
分析
此算法是欧拉筛法求质数,欧拉筛是线性筛法,即所有的合数都被它最小的质因子筛一次,减少了埃氏筛法的重复筛的次数,时间复杂度近似O(n)
32.在执行完init()后,f[1],f[2],f[3]… f[100]中有( C )个等于2.
A. 23
B. 24
C. 25
D. 26
分析
f数组是约数个数,约数个数和为2,表示对应数组下标的数为质数
1~100之间的质数有25个,分别是
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
33.(4分)当输入为"1000"时,输出为( C )
A. “15 1340”
B. “15 2340”
C. “16 2340”
D. “16 1340”
分析
由程序逻辑知分别输出1000对应的约数个数及其对应的约数和
1000=2^3 * 5^3第1项求约数个数,根据约数个数公式
(3+1)*(3+1)=16
第2项求约数和,根据约数和公式
(2^0+2^1+2^2+2^3) * (5^0+5^1+5^2+5^3)=2340
所以选C
相关文章:

信息学奥赛初赛天天练-38-CSP-J2021阅读程序-约数个数、约数和、埃氏筛法、欧拉筛法筛素数应用
PDF文档公众号回复关键字:20240628 2021 CSP-J 阅读程序3 1阅读程序(判断题1.5分 选择题3分 共计40分 ) 01 #include<stdio.h> 02 using namespace std; 03 04 #define n 100000 05 #define N n1 06 07 int m; 08 int a[N],b[N],c[N],d[N]; 09 int f[N],g[N]; 10 11 …...
第100+13步 ChatGPT学习:R实现决策树分类
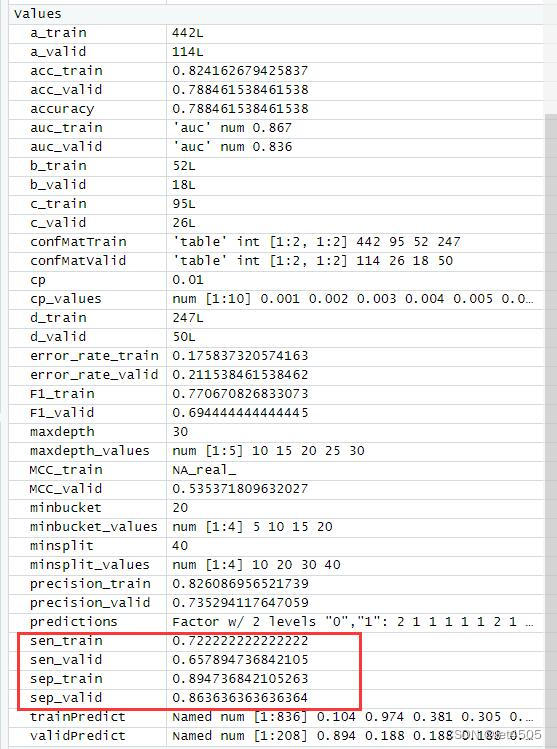
基于R 4.2.2版本演示 一、写在前面 有不少大佬问做机器学习分类能不能用R语言,不想学Python咯。 答曰:可!用GPT或者Kimi转一下就得了呗。 加上最近也没啥内容写了,就帮各位搬运一下吧。 二、R代码实现决策树分类 (…...

Hi3861 OpenHarmony嵌入式应用入门--LiteOS MessageQueue
CMSIS 2.0接口中的消息(Message)功能主要涉及到实时操作系统(RTOS)中的线程间通信。在CMSIS 2.0标准中,消息通常是通过消息队列(MessageQueue)来进行处理的,以实现不同线程之间的信息…...

ffmpeg编码图象时报错Invalid buffer size, packet size * < expected frame_size *
使用ffmpeg将单个yuv文件编码转为jpg或其他图像格式时,报错: Truncating packet of size 11985408 to 3585 [rawvideo 0x1bd5390] Packet corrupt (stream 0, dts 1). image_3264_2448_0.yuv: corrupt input packet in stream 0 [rawvideo 0x1bd7c60…...

解决类重复的问题
1.针对AndroidX 类重复问题 解决办法: android.useAndroidXtrue android.enableJetifiertrue2.引用其他sdk出现类重复的问题解决办法:configurations {all { // You should exclude one of them not both of themexclude group: "com.enmoli"…...

使用 shell 脚本 统计app冷启动耗时
下面是一个 shell 脚本,它使用 参数将包名称作为参数--app,识别相应应用程序进程的 PID,使用 终止该进程adb shell kill,最后使用 重新启动该应用程序adb shell am start: #!/bin/bash# Check if package name is pro…...
使用容器部署redis_设置配置文件映射到本地_设置存储数据映射到本地_并开发java应用_连接redis---分布式云原生部署架构搭建011
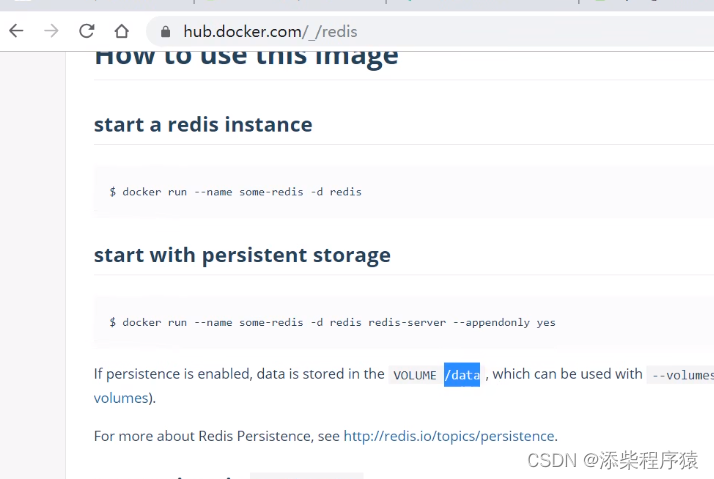
可以看到java应用的部署过程,首先我们要准备一个java应用,并且我们,用docker,安装一个redis 首先我们去start.spring.io 去生成一个简单的web项目,然后用idea打开 选择以后下载 放在这里,然后我们去安装redis 在公共仓库中找到redis . 可以看到它里面介绍说把数据放到了/dat…...

第五节:如何使用其他注解方式从IOC中获取bean(自学Spring boot 3.x的第一天)
大家好,我是网创有方,上节我们实践了通过Bean方式声明Bean配置。咱们这节通过Component和ComponentScan方式实现一个同样功能。这节实现的效果是从IOC中加载Bean对象,并且将Bean的属性打印到控制台。 第一步:创建pojo实体类studen…...

Paragon NTFS与Tuxera NTFS有何区别 Mac NTFS 磁盘读写工具选哪个好
macOS系统虽然以稳定、安全系数高等优点著称,但因其封闭性,不能对NTFS格式磁盘写入数据常被人们诟病。优质的解决方案是使用磁盘管理软件Paragon NTFS for Mac(点击获取激活码)和Tuxera NTFS(点击获取激活码࿰…...

EtherCAT主站IGH-- 2 -- IGH之coe_emerg_ring.h/c文件解析
EtherCAT主站IGH-- 2 -- IGH之coe_emerg_ring.h/c文件解析 0 预览一 该文件功能coe_emerg_ring.c 文件功能函数预览 二 函数功能介绍coe_emerg_ring.c 中主要函数的作用1. ec_coe_emerg_ring_init2. ec_coe_emerg_ring_clear3. ec_coe_emerg_ring_size4. ec_coe_emerg_ring_pus…...

psensor 的手势功能
psensor 的手势功能的移植过程 有时间再来写下...
使用 nvm 管理 Node 版本及 pnpm 安装
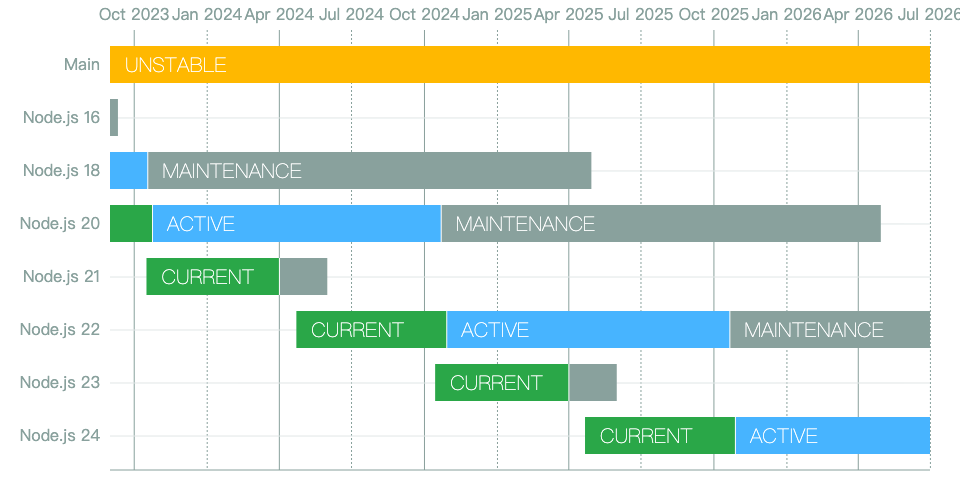
文章目录 GithubWindows 环境Mac/Linux 使用脚本进行安装或更新Mac/Linux 环境变量nvm 常用命令npm 常用命令npm 安装 pnpmNode 历史版本 Github https://github.com/nvm-sh/nvm Windows 环境 https://nvm.uihtm.com/nvm.html Mac/Linux 使用脚本进行安装或更新 curl -o- …...
uni-appx使用form表单页面初始化报错
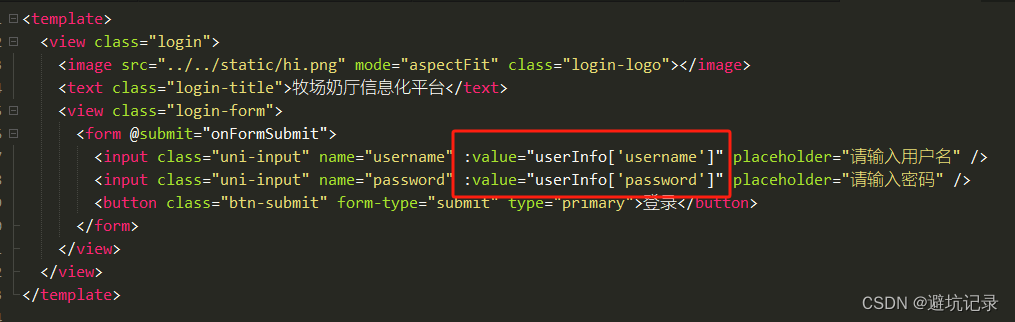
因为UniFormSubmitEvent的类型时 e-->detail-->value,然后没有了具体值。所以页面初始化的时候 不能直接从value取值,会报错找不到 所以form表单里的数据我们要设置成一个对象来存放 这个问题的关键在于第22行代码 取值: 不能按照点的方式取值 …...

TiDB-从0到1-数据导出导入
TiDB从0到1系列 TiDB-从0到1-体系结构TiDB-从0到1-分布式存储TiDB-从0到1-分布式事务TiDB-从0到1-MVCCTiDB-从0到1-部署篇TiDB-从0到1-配置篇TiDB-从0到1-集群扩缩容 一、数据导出 TiDB中通过Dumpling来实现数据导出,与MySQL中的mysqldump类似,其属于…...
代码实践 -卷积神经网络-16自定义层)
动手学深度学习(Pytorch版)代码实践 -卷积神经网络-16自定义层
16自定义层 import torch import torch.nn.functional as F from torch import nnclass CenteredLayer(nn.Module):def __init__(self):super().__init__()#从其输入中减去均值#X.mean() 计算的是整个张量的均值#希望计算特定维度上的均值,可以传递 dim 参数。#例如…...

树莓派4设置
使用sudo命令时要求输入密码 以 sudo 为前缀的命令以超级用户身份运行。默认情况下,超级用户不需要密码。不过,您可以要求所有以 sudo 运行的命令都输入密码,从而提高 Raspberry Pi 的安全性。 要强制 sudo 要求输入密码,请为你…...

44.商城系统(二十五):k8s基本操作,ingress域名访问,kubeSphere可视化安装
上一章我们已经配置好了k8s集群,如果没有配置好先去照着上面的配。 一、k8s入门操作 1.部署一个tomcat,测试容灾恢复 #在主机器上执行 kubectl create deployment tomcat6 --image=tomcat:6.0.53-jre8#查看k8s中的所有资源 kubectl get all kubectl get all -o wide#查看po…...

MySQL高级查询
MySQL 前言 文本源自微博客 (www.microblog.store),且已获授权. 一. mysql基础知识 1. mysql常用系统命令 启动命令 net start mysql停止命令 net stop mysql登录命令 mysql -h ip -P 端口 -u 用户名 -p 本机可以省略 ip mysql -u 用户名 -p 查看数据库版本 mysql --ve…...

聊聊啥项目适合做自动化测试
作为测试从业者,你是否遇到过这样的场景,某天公司大Boss找你谈话。 老板:小李,最近工作辛苦了 小李:常感谢您的认可,这不仅是对我个人的鼓励,更是对我们整个团队努力的认可。我们的成果离不开每…...

ROS2开发机器人移动
.创建功能包和节点 这里我们设计两个节点 example_interfaces_robot_01,机器人节点,对外提供控制机器人移动服务并发布机器人的状态。 example_interfaces_control_01,控制节点,发送机器人移动请求,订阅机器人状态话题…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
