素数筛(算法篇)
算法之素数筛
素数筛
引言:
素数(质数):除了1和自己本身之外,没有任何因子的数叫做素数(质数)
朴素筛法(优化版)
概念:
朴素筛法:是直接暴力枚举2到当前判断的数x(不包括),然后看在这范围内是否存在因子,如果存在就不是素数,不存在就是素数,时间复杂度为O(n*n)优化版:优化版是用到了一个数学性质进行优化,使其只需要判断2到sqrt(x)的范围内,是否存在x的因子即可,时间复杂度为O(n*sqrt(n))
数学性质:如果一个数x能够被一个大于1且小于等于sqrt(x)的整数整除,那么x必定能够被另一个大于1且大于sqrt(x)的整数整除。
#include <iostream>
using namespace std;//朴素筛素数判断算法时间复杂度:O(n)
bool isprime1(int x){if(x==1) return false;if(x==2) return true;for(int i=2;i<x;++i){if(x%i==0) return false;}return true;
}//优化版素数判断算法时间复杂度:O(sqrt(n))
bool isprime(int x){if(x==1) return false;if(x==2) return true;for(int i=2;i<x/i;++i){if(x%i==0) return false;}return true;
}int main() {//假设筛选出1-1000的素数for(int i=1;i<=1000;i+=2){if(isprime(i)) cout<<i<<endl;}system("pause");return 0;
}
欧拉筛(线性筛)
概念:
欧拉筛:利用合数的数学性质,可以将素数筛的算法优化到时间复杂度为O(n)
合数:除了1和自身之外还有其他正因子(除了 1 和自身以外的能够整除它的正整数),并且大于1的整数
数学性质:对于任意一个合数 x,它一定可以被其最小质因数(即最小的能整除 x 的质数)整除
算法具体操作:
- 初始化一个标记数组vis[]和记录素数数组prime,vis所有元素初始化为false
- 从2遍历到n(要筛选素数范围),如果vis[i]为false,则将i标记为素数,并将i记录在prime数组中,并将i的倍数j(j=i*i,i*i+i…)标记为合数(true)
- 遍历完所有的数后,prime数组中的数都为素数
总结:
在这个过程中,每个合数都会被标记为其最小质因数,这样能够确保每个合数只会被标记一次。由于每个合数只会被其最小质因数标记,因此在遍历过程中,每个合数只会被标记一次,而非多次,从而避免了重复标记,提高了效率。
const int N=1e8+10;
int prime[N];
bool vis[N];//欧拉筛总体时间复杂度为O(n)
void isprimes(int n){int cnt=0;for(int i=2;i<=n;++i){if(!vis[i]) prime[cnt++]=i;for(int j=0;prime[j]<=n/i;++j){vis[i*prime[j]]=true;if(i%prime[j]==0) break;}}
}
尾言
完整版笔记也就是数据结构与算法专栏完整版可到我的博客进行查看,或者在github库中自取(包含源代码)
- 博客1: codebooks.xyz
- 博客2:moonfordream.github.io
- github项目地址:Data-Structure-and-Algorithms
相关文章:
)
素数筛(算法篇)
算法之素数筛 素数筛 引言: 素数(质数):除了1和自己本身之外,没有任何因子的数叫做素数(质数) 朴素筛法(优化版) 概念: 朴素筛法:是直接暴力枚举2到当前判断的数x(不包括),然后看在这范围内是否存在因…...

迁移Microsoft Edge
如何将Microsoft Edge迁移到d盘?对于Microsoft Edge想必大部分人都不陌生,它是Windows操作系统的默认浏览器,存储用户的个人数据、缓存和设置等信息。有些时候,我们需要对Microsoft Edge中的数据进行数据迁移,以释放c盘…...
Maven高级理解属性
属性 在这一章节内容中,我们将学习两个内容,分别是 属性版本管理 属性中会继续解决分模块开发项目存在的问题,版本管理主要是认识下当前主流的版本定义方式。 4.1 属性 4.1.1 问题分析 讲解内容之前,我们还是先来分析问题: …...

Trilium Notes浏览器插件保存网页内容到docker私有化部署
利用Trilium浏览器插件可以很方便的把网页内容保存到Trilium,需要先在docker部署好trilium,还没有部署的可以先看这篇文章:trilium笔记私有化部署-www.88531.cn资享网 1.下载Trilium浏览器插件:https://www.npspro.cn/33462.html…...

C++ 统计二进制串中0出现的个数
描述 一个32位有符号整数,使用二进制来表示,现在要统计一下二进制串中0的个数。 示例1 输入: 11 返回值: 29 说明: 二进制00000000000000000000000000001011中有29位0 class Solution { public:/*** 代码中的…...

note-网络是怎样连接的6 请求到达服务器,响应返回浏览器
助记提要 服务器程序的结构套接字的指代方式MAC模块的接收过程IP模块的接收过程TCP模块处理连接包TCP模块处理数据包TCP模块的断开操作URI转换为实际文件路径URI调用程序Web服务器访问控制响应内容的类型 6章 请求到达服务器,响应返回浏览器 1 服务器概览 在数据…...
)
存储过程与函数:封装数据库逻辑的艺术(七)
引言 在上一章《事务处理》中,我们深入探讨了事务的ACID特性以及如何通过事务控制语句和隔离级别来确保数据的一致性和完整性。本章,我们将把焦点转向存储过程与函数,这是数据库系统中用于封装复杂业务逻辑和增强代码复用性的强大工具。通过…...
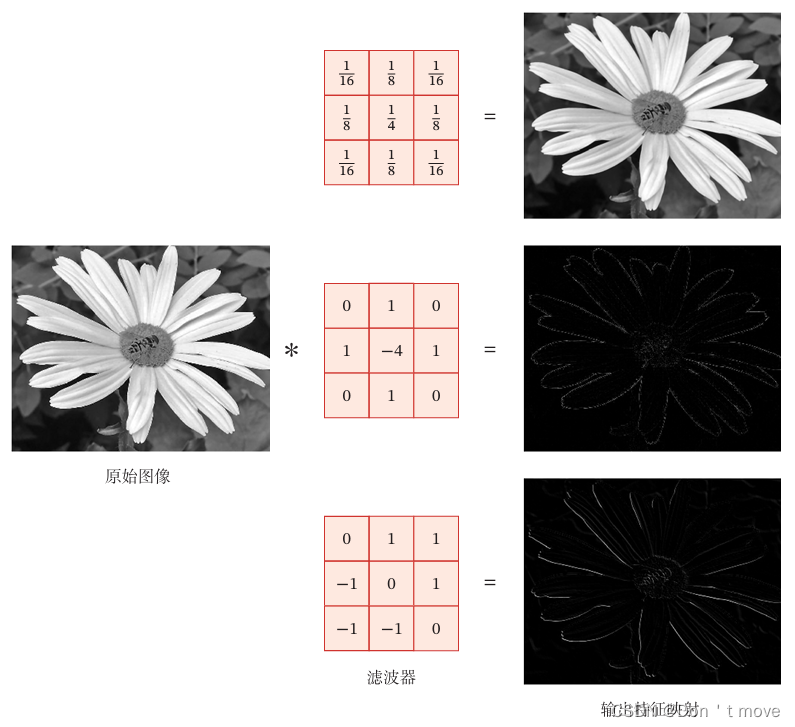
【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】卷积
卷积经常用在信号处理中,用于计算信号的延迟累积。假设一个信号发射器每个时刻 t t t产生一个信号 x t x_t xt,其信息的衰减率为 w k w_k wk,即在 k − 1 k-1 k−1个时间步长后,信息为原来的 w k w_k wk倍,时刻 …...

Trie字符串统计
Trie字符串统计 维护一个字符串集合,支持两种操作: I x 向集合中插入一个字符串 x;Q x 询问一个字符串在集合中出现了多少次。 共有 N个操作,所有输入的字符串总长度不超过 105,字符串仅包含小写英文字母。 输入格式…...

Kali Linux源
中科大 deb http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib deb-src http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib阿里云 deb http://mirrors.aliyun.com/kali kali-rolling main non-free contrib deb-src http://mirrors.…...
【RT摩拳擦掌】基于RT106L/S语音识别的百度云控制系统
【RT摩拳擦掌】基于RT106L/S语音识别的百度云控制系统 一 文档简介二 平台构建2.1 使用平台2.2 百度智能云2.2.1 物联网核心套件2.2.2 在线语音合成 2.3 playback语音数据准备与烧录2.4 开机语音准备与添加2.5 唤醒词识别词命令准备与添加 三 代码准备3.1 sln-local/2-iot 代码…...
国标GB28181视频汇聚平台EasyCVR设备展示数量和显示条数不符的原因排查与解决
国标GB28181/GA/T1400协议/安防综合管理系统EasyCVR视频汇聚平台能在复杂的网络环境中,将前端设备统一集中接入与汇聚管理。智慧安防/视频存储/视频监控/视频汇聚EasyCVR平台可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级…...

FastAPI教程I
本文参考FastAPI教程https://fastapi.tiangolo.com/zh/tutorial 第一步 import uvicorn from fastapi import FastAPIapp FastAPI()app.get("/") async def root():return {"message": "Hello World"}if __name__ __main__:uvicorn.run(&quo…...

如何在 HTML 中实现响应式设计以适应不同设备的屏幕尺寸?
要在HTML中实现响应式设计以适应不同设备的屏幕尺寸,可以使用CSS媒体查询和流动布局。 以下是实现响应式设计的一些关键步骤: 使用CSS媒体查询:CSS媒体查询允许根据屏幕尺寸和设备特性应用不同的CSS样式。通过在CSS中使用media规则…...

【基础篇】第1章 Elasticsearch 引言
1.1 Elasticsearch简介 1.1.1 基本概念 Elasticsearch,一个开源的分布式搜索引擎,以其强大的搜索能力和实时数据分析能力,在大数据时代脱颖而出。它基于Apache Lucene库构建,旨在提供高效、可扩展且易于使用的全文检索解决方案。…...

在区块链技术广泛应用的情况下,C 语言如何在区块链的底层开发中发挥更有效的作用,提高性能和安全性?
C语言在区块链底层开发中发挥着重要的作用,可以提高性能和安全性。具体可以从以下几个方面进行优化: 性能优化:C语言是一种高效的编程语言,可以直接访问内存和硬件资源。在区块链底层开发中,使用C语言可以更好地利用底…...

量化投资 日周月报 2024-06-28
文章 深度学习在量化交易中的应用:在BigQuant量化交易平台的文章中,探讨了深度学习在量化交易中,特别是在因子挖掘方面的应用。文章提到,随着传统线性模型的潜力逐渐枯竭,非线性模型逐渐成为量化交易的主要探索方向。深度学习因其对非线性关系的拟合能力,在量化交易中展现…...
基于 Paimon 的袋鼠云实时湖仓入湖实战剖析
在当今数据驱动的时代,企业对数据的实施性能力提出了前所未有的高要求。为了应对这一挑战,构建高效、灵活且可扩展的实时湖仓成为数字化转型的关键。本文将深入探讨袋鼠云数栈如何通过三大核心实践——ChunJun 融合 Flink CDC、MySQL 一键入湖至 Paimon …...

IPython相关了解
一、什么是 IPython? 1.1 简单理解 IPython IPython 是一种增强的 Python 交互式解释器,它可以让你更方便地编写、调试和运行 Python 代码。你可以把它想象成一个比普通 Python 解释器更聪明、功能更丰富的工具,非常适合用来进行数据探索、…...
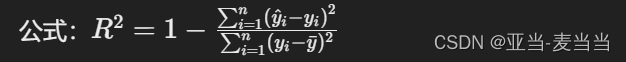
华为面试题及答案——机器学习(二)
21. 如何评价分类模型的优劣? (1)模型性能指标 准确率(Accuracy): 定义:正确分类的样本数与总样本数之比。适用:当各类样本的数量相对均衡时。精确率(Precision): 定义:预测为正类的样本中实际为正类的比例。适用:当关注假阳性错误的成本较高时(例如垃圾邮件检测…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
