二刷算法训练营Day45 | 动态规划(7/17)
目录
详细布置:
1. 139. 单词拆分
2. 多重背包理论基础
3. 背包总结
3.1 背包递推公式
3.2 遍历顺序
01背包
完全背包
详细布置:
1. 139. 单词拆分
给你一个字符串
s和一个字符串列表wordDict作为字典。如果可以利用字典中出现的一个或多个单词拼接出s则返回true。注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。
拆分时可以重复使用字典中的单词,说明就是一个完全背包!
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
2. 确定递推公式
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
3. dp数组如何初始化
从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]就是递推的根基,dp[0]一定要为true,否则递推下去后面都都是false了。
那么dp[0]有没有意义呢?
dp[0]表示如果字符串为空的话,说明出现在字典里。
但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况,那么dp[0]初始为true完全就是为了推导公式。
下标非0的dp[i]初始化为false,只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。
4. 确定遍历顺序
题目中说是拆分为一个或多个在字典中出现的单词,所以这是完全背包。
还要讨论两层for循环的前后顺序。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
我在这里做一个总结:
求组合数:动态规划:518.零钱兑换II (opens new window)求排列数:动态规划:377. 组合总和 Ⅳ (opens new window)、动态规划:70. 爬楼梯进阶版(完全背包) (opens new window)求最小数:动态规划:322. 零钱兑换 (opens new window)、动态规划:279.完全平方数(opens new window)
而本题其实我们求的是排列数,为什么呢。 拿 s = "applepenapple", wordDict = ["apple", "pen"] 举例。
"apple", "pen" 是物品,那么我们要求 物品的组合一定是 "apple" + "pen" + "apple" 才能组成 "applepenapple"。
"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的,那么我们就是强调物品之间顺序。
所以说,本题一定是 先遍历 背包,再遍历物品。
5. 举例推导dp[i]
class Solution:def backtracking(self, s: str, wordSet: set[str], startIndex: int) -> bool:# 边界情况:已经遍历到字符串末尾,返回Trueif startIndex >= len(s):return True# 遍历所有可能的拆分位置for i in range(startIndex, len(s)):word = s[startIndex:i + 1] # 截取子串if word in wordSet and self.backtracking(s, wordSet, i + 1):# 如果截取的子串在字典中,并且后续部分也可以被拆分成单词,返回Truereturn True# 无法进行有效拆分,返回Falsereturn Falsedef wordBreak(self, s: str, wordDict: List[str]) -> bool:wordSet = set(wordDict) # 转换为哈希集合,提高查找效率return self.backtracking(s, wordSet, 0)
2. 多重背包理论基础
多重背包在面试中基本不会出现,力扣上也没有对应的题目,大家对多重背包的掌握程度知道它是一种01背包,并能在01背包的基础上写出对应代码就可以了。
例题可以见卡哥的总结:多重背包
3. 背包总结
关于这几种常见的背包,其关系如下:
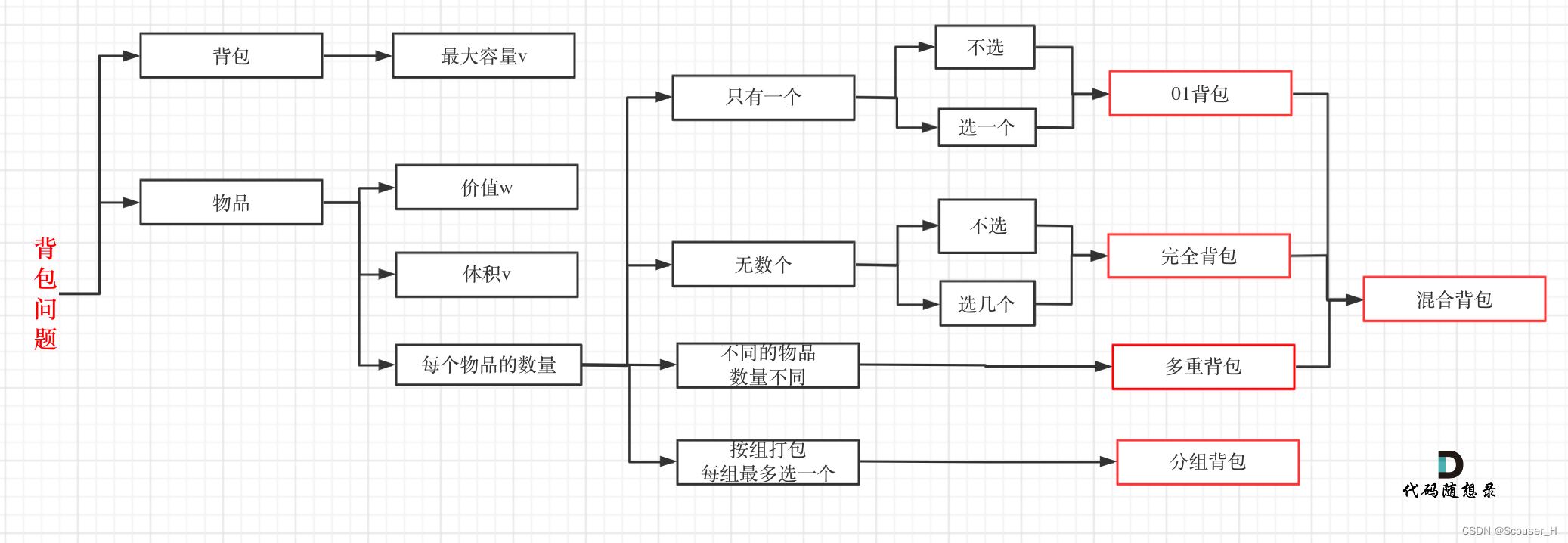
通过这个图,可以很清晰分清这几种常见背包之间的关系。
在讲解背包问题的时候,我们都是按照如下五部来逐步分析,相信大家也体会到,把这五部都搞透了,算是对动规来理解深入了。
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
其实这五部里哪一步都很关键,但确定递推公式和确定遍历顺序都具有规律性和代表性,所以下面我从这两点来对背包问题做一做总结
3.1 背包递推公式
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
- 动态规划:416.分割等和子集(opens new window)
- 动态规划:1049.最后一块石头的重量 II(opens new window)
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
- 动态规划:474.一和零(opens new window)
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
- 动态规划:322.零钱兑换(opens new window)
- 动态规划:279.完全平方数
3.2 遍历顺序
01背包
在动态规划:关于01背包问题,你该了解这些! (opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
和动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的,大家需要注意!
完全背包
说完01背包,再看看完全背包。
在动态规划:关于完全背包,你该了解这些! (opens new window)中,讲解了纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
但是仅仅是纯完全背包的遍历顺序是这样的,题目稍有变化,两个for循环的先后顺序就不一样了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关题目如下:
- 求组合数:动态规划:518.零钱兑换II(opens new window)
- 求排列数:动态规划:377. 组合总和 Ⅳ (opens new window)、动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
- 求最小数:动态规划:322. 零钱兑换 (opens new window)、动态规划:279.完全平方数(opens new window)
对于背包问题,其实递推公式算是容易的,难是难在遍历顺序上,如果把遍历顺序搞透,才算是真正理解了。
相关文章:

二刷算法训练营Day45 | 动态规划(7/17)
目录 详细布置: 1. 139. 单词拆分 2. 多重背包理论基础 3. 背包总结 3.1 背包递推公式 3.2 遍历顺序 01背包 完全背包 详细布置: 1. 139. 单词拆分 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单…...
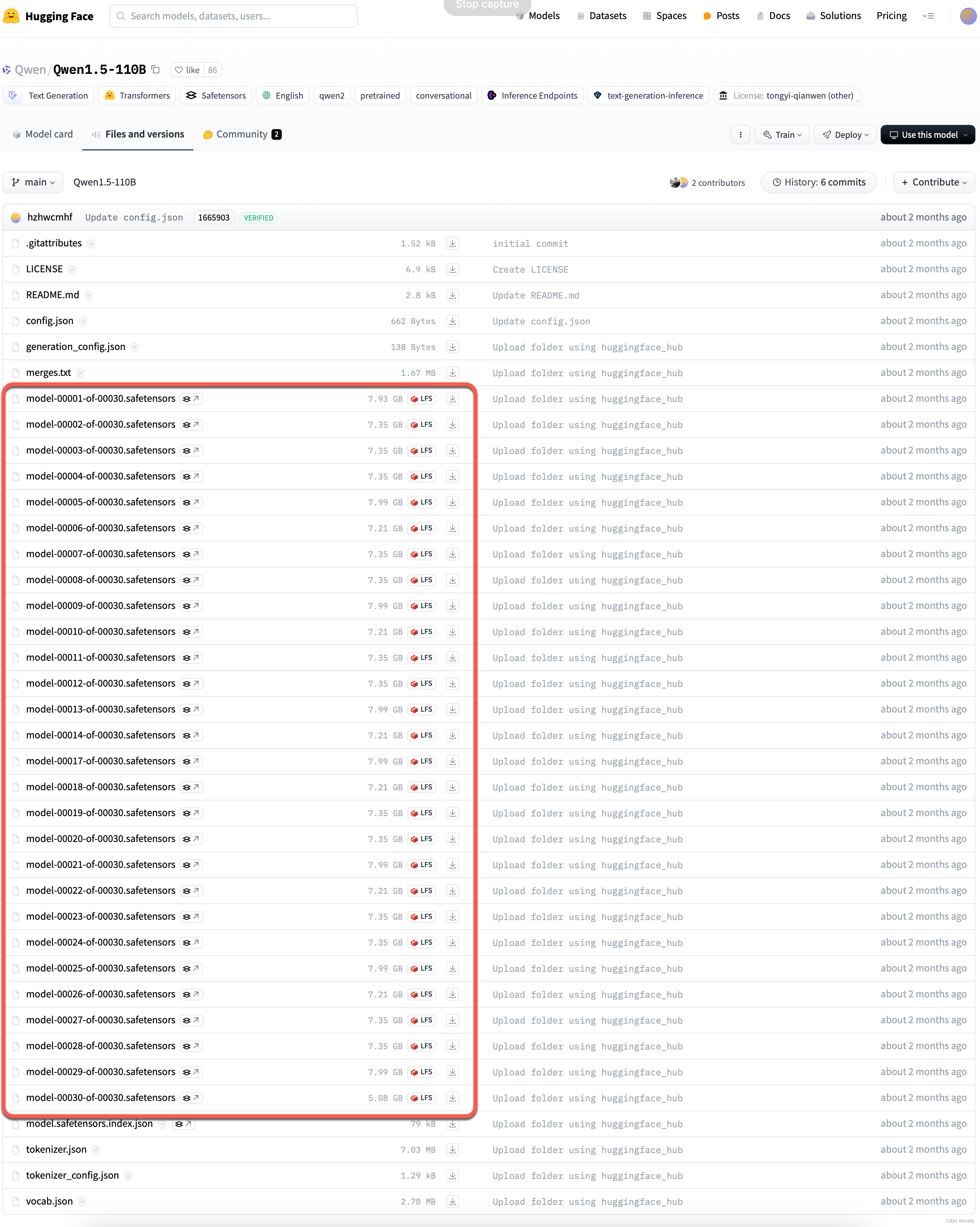
大模型项目落地时,该如何估算模型所需GPU算力资源
近期公司有大模型项目落地。在前期沟通时,对于算力估算和采购方案许多小伙伴不太了解,在此对相关的算力估算和选择进行一些总结。 不喜欢过程的可以直接 跳到HF上提供的模型计算器 要估算大模型的所需的显卡算力,首先要了解大模型的参数基础知识。 大模型的规模、参数的理解…...

LLM应用开发-RAG系统评估与优化
前言 Hello,大家好,我是GISer Liu😁,一名热爱AI技术的GIS开发者,在上一篇文章中,我们学习了如何基于LangChain构建RAG应用,并且通过Streamlit将这个RAG应用部署到了阿里云服务器;&am…...
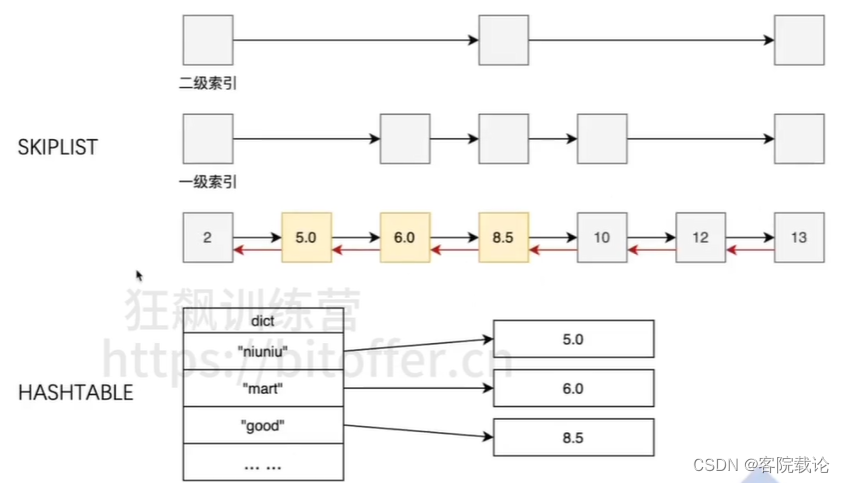
秋招突击——第七弹——Redis快速入门
文章目录 引言Redis是什么 正文对象String字符串面试重点 List面试考点 压缩列表ZipList面试题 Set面试题讲解 Hash面试重点 HASHTABLE底层面试考点 跳表面试重点 ZSET有序链表面试重点 总结 引言 在项目和redis之间,我犹豫了一下,觉得还是了解学习一下…...
软考初级网络管理员__操作系统单选题
1.在Windows资源管理器中,假设已经选定文件,以下关于“复制”操作的叙述中,正确的有()。 按住Ctr键,拖至不同驱动器的图标上 按住AIt键,拖至不同驱动器的图标上 直接拖至不同驱动器的图标上 按住Shift键࿰…...
)
从入门到精通:网络编程套接字(万字详解,小白友好,建议收藏)
一、预备知识 1.1 理解源IP地址和目的IP地址 在网络编程中,IP地址(Internet Protocol Address)是每个连接到互联网的设备的唯一标识符。IP地址可以分为IPv4和IPv6两种类型。IPv4地址是由32位二进制数表示,通常分为四个八位组&am…...

dledger原理源码分析系列(一)架构,核心组件和rpc组件
简介 dledger是openmessaging的一个组件, raft算法实现,用于分布式日志,本系列分析dledger如何实现raft概念,以及dledger在rocketmq的应用 本系列使用dledger v0.40 本文分析dledger的架构,核心组件;rpc组…...

第七节:如何浅显易懂地理解Spring Boot中的依赖注入(自学Spring boot 3.x的第二天)
大家好,我是网创有方,今天我开始学习spring boot的第一天,一口气写了这么多。 这节通过一个非常浅显易懂的列子来讲解依赖注入。 在Spring Boot 3.x中,依赖注入(Dependency Injection, DI)是一个核心概念…...

Postman自动化测试实战:使用脚本提升测试效率
在软件开发过程中,接口测试是确保后端服务稳定性和可靠性的关键步骤。Postman作为一个流行的API开发工具,提供了强大的脚本功能来实现自动化测试。通过在Postman中使用脚本,测试人员可以编写测试逻辑,实现测试用例的自动化执行&am…...

CSMA/CA并不是“公平”的
CSMA/CA会造成过于公平,对于最需要流量的节点,是最不友好的,而对于最不需要流量的节点,则是最友好的。 CSMA/CA是优先公平来工作的。 CSMA/CA首先各节点使用DIFS界定air idle,在此期间大家都等待 其次,为了同时发送引起碰撞,在DIFS之后随机从CWmin和CWmax之间选择一个时…...

【漏洞复现】I doc view——任意文件读取
声明:本文档或演示材料仅供教育和教学目的使用,任何个人或组织使用本文档中的信息进行非法活动,均与本文档的作者或发布者无关。 文章目录 漏洞描述漏洞复现测试工具 漏洞描述 I doc view 在线文档预览是一个用于查看、编辑、管理文档的工具…...
图数据库 vs 向量数据库
最近大模型出来之后,向量数据库重新翻红,业界和市场上有不少声音认为向量数据库会极大的影响图数据库,图数据库市场会萎缩甚至消失,今天就从技术原理角度来讨论下图数据库和向量数据库到底差别在哪里,适合什么场景&…...

企业品牌出海第一站 维基百科词条创建
维基百科是一部内容开放、自由的网络百科全书,旨在创造一个涵盖所有领域知识,服务所有互联网用户的知识性百科全书。其在国外应用非常广泛且认可度很高,国内品牌出海或国际品牌都很有必要创建企业自己的维基百科页面,以及企业高管的个人维基百科页面。 如…...
Windows下activemq集群配置(broker-network)
1.activemq版本信息 activemq:apache-activemq-5.18.4 2.activemq架构 3.activemq集群配置 activemq集群配置基于Networks of Brokers 这种HA方案的优点:是占用的节点数更少(只需要2个节点),而且2个broker都可以响应消息的接收与发送。不足ÿ…...
心理辅导平台系统
摘 要 中文本论文基于Java Web技术设计与实现了一个心理辅导平台。通过对国内外心理辅导平台发展现状的调研,本文分析了心理辅导平台的背景与意义,并提出了论文研究内容与创新点。在相关技术介绍部分,对Java Web、SpringBoot、B/S架构、MVC模…...

代理IP对SEO影响分析:提升网站排名的关键策略
你是否曾经为网站排名难以提升而苦恼?代理服务器或许就是你忽略的关键因素。在竞争激烈的互联网环境中,了解代理服务器对SEO的影响,有助于你采取更有效的策略,提高网站的搜索引擎排名。本文将为你详细分析代理服务器在SEO优化中的…...

【leetcode--三数之和】
这道题记得之前做过,但是想不起来了。。总结一下: 函数的主要步骤和关键点: 排序:对输入的整数数组nums进行排序。这是非常重要的,因为它允许我们使用双指针技巧来高效地找到满足条件的三元组。初始化:定…...

解决Java中的ClassCastException问题
解决Java中的ClassCastException问题 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在Java编程中,ClassCastException是一个常见的运行时异常&am…...

【TensorFlow深度学习】混合生成模型:结合AR与AE的创新尝试
混合生成模型:结合AR与AE的创新尝试 引言自回归模型与自动编码器的简述混合模型的创新尝试组合AR与AE:MADE混合模型在图学习中的应用 结论与展望 在自我监督学习的广阔天地里,混合生成模型以其独特的魅力,跨越了自回归(…...

Spring:Spring中分布式事务解决方案
一、前言 在Spring中,分布式事务是指涉及多个数据库或系统的事务处理,其中事务的参与者、支持事务的服务器、资源管理器以及事务管理器位于分布式系统的不同节点上。这样的架构使得两个或多个网络计算机上的数据能够被访问并更新,同时将这些操…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
