图论·多源最短路径Floyddijsktra
例题地址
多源最短路径
- 多个源点多个终点
- 可以使用Floyd算法直接求各源点到终点的最短距离,也可以直接多次使用dijsktra算法求单源点到终点的最短距离
Floyd算法
使用条件
- 多源最短路径
- 权值正负皆可
核心思想:动态规划
- 子问题:
- 设(A,B)表示顶点A,B之间的距离,则有可能(A,B)=(A,C)+(C,B),这说明AB之间的距离可以继续分解为AC,CB之间的距离问题,我们可以找到一个子问题,而这就体现了动态规划的思想
- 定义dp数组:
- 因为从存储上来讲,我们需要利用邻接矩阵,所以AB间的最短距离表示至少需要两个维度i和j,所以dp数组至少有两个维度。
- 又因为从子问题的角度,我们分解问题的出发点是找一个中间结点,比较AB的最短距离经过中间结点C会不会更短。所以定义一个新的维度k,其含义是考虑下标从1开始到k结束的k个顶点是否应该加入到路径中去。(这个定义有鲜明的dp特色,学过dp应该不难理解)
因此dp数组的定义如下dp[i][j][k],表示考虑下标1~k的k个顶点的 i到j的最短距离
- 递推公式:
- 根据定义,不难想到,递推公式就是是否应该将下标为k的结点是否值得加入到路径中去
- 不加入k结点:
dp[i][j][k - 1](言外之意就是i和j已经连通,加入k结点不值得) - 加入k结点:
dp[i][k][k - 1] + dp[k][j][k - 1] - 完整公式:
dp[i][j][k] = min(dp[i][j][k - 1], dp[i][k][k - 1] + dp[k][j][k - 1]);
- 初始化:
- 处理输入时,要考虑k这个维度应该怎么设置。一种简单的想法是,把k设置无关紧要或者无意义的数值(根据不同题目需要可能是INT_MAX/INT_MIN/0),这里设置为0
dp[u][v][0] = w;
- 处理输入时,要考虑k这个维度应该怎么设置。一种简单的想法是,把k设置无关紧要或者无意义的数值(根据不同题目需要可能是INT_MAX/INT_MIN/0),这里设置为0
- 遍历顺序:
- 其实这个很简单,根据递推公式,
dp[i][j][k-1]中k-1个维度的数据必须知道,否则会造成无意义的更新,所以k必须在外层循环
- 其实这个很简单,根据递推公式,
个人代码
using namespace std;
using ll = long long;
int n, m, u, v, w,q,start,ed;
void solve() {cin >> n >> m;vector < vector<vector<int>>>dp(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10009)));//dp数组while (m--) {cin >> u >> v >> w;dp[u][v][0] = w;dp[v][u][0] = w;}for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {dp[i][j][k] = min(dp[i][j][k - 1], dp[i][k][k - 1] + dp[k][j][k - 1]);}}}cin >> q;while (q--) {cin >> start >> ed;cout << (dp[start][ed][n] == 10009 ? -1 : dp[start][ed][n])<<endl;}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
注意事项
+dp数组不应该设置为最大值INT_MAX,否则会相加溢出导致数据异常
vector < vector<vector<int>>>dp(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10009)));
空间优化版
- 直接删去了k这一个维度,因为利用更新后的数据(第k层的)
dp[i][k] + dp[k][j]更新自己同一层(第k层的)数据,也能得到正确结果
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, u, v, w,q,start,ed;
void solve() {cin >> n >> m;vector < vector<int>>dp(n + 1,vector<int>(n+1,10009));//dp数组while (m--) {cin >> u >> v >> w;dp[u][v] = w;dp[v][u] = w;}for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);}}}cin >> q;while (q--) {cin >> start >> ed;cout << (dp[start][ed] == 10009 ? -1 : dp[start][ed])<<endl;}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
多次使用dijsktra算法
核心思路
- 将dijsktra定义为函数
- 传入dist数组的拷贝(没有&引用)作参数,传入st,ed分别作为源点和终点,在函数内初始化dist数组
个人代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, s, e, v,q,st,ed;//s=u,e=v,v=w;
void dijkstra(vector<vector<int>>&grid, vector<bool>visited, vector<int>dist,int st,int ed) {
//vector<bool>visited和vector<int>dist一定不能传入引用的形式!dist[st]=0;//一定要在这里初始化dist[st]for (int i = 1; i <= n - 1; i++) {int temp = INT_MAX;int cur = 0;for (int j = 1; j <= n; j++) {if (!visited[j] && dist[j] < temp) {temp = dist[j];cur = j;}}visited[cur] = true;for (int j = 1; j <= n; j++) {if (grid[cur][j] != INT_MAX && !visited[j] && dist[cur] + grid[cur][j] < dist[j]) {dist[j] = dist[cur] + grid[cur][j];}}}cout << (dist[ed] == INT_MAX ? -1 : dist[ed]) << endl;
}
void solve() {cin >> n >> m;vector<vector<int>>grid(n + 1, vector<int>(n + 1, INT_MAX));vector<bool>visited(n + 1, false);vector<int>dist(n + 1, INT_MAX);while (m--) {cin >> s >> e >> v;grid[s][e] = v;grid[e][s] = v;}cin >> q;while (q--) {cin >> st >> ed;dijkstra(grid, visited, dist,st,ed);}}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
本文参考于代码随想录
相关文章:

图论·多源最短路径Floyddijsktra
例题地址 多源最短路径 多个源点多个终点可以使用Floyd算法直接求各源点到终点的最短距离,也可以直接多次使用dijsktra算法求单源点到终点的最短距离 Floyd算法 使用条件 多源最短路径权值正负皆可 核心思想:动态规划 子问题: 设(A,B)…...
微服务 | Springboot整合GateWay+Nacos实现动态路由
1、简介 路由转发 执行过滤器链。 网关,旨在为微服务架构提供一种简单有效的统一的API路由管理方式。同时,基于Filter链的方式提供了网关的基本功能,比如:鉴权、流量控制、熔断、路径重写、黑白名单、日志监控等。 基本功能…...

做google SEO 有哪些好用的工具?这12款谷歌SEO工具值得收藏!
1、Google Trends 谷歌旗下一款基于搜索数据推出的一款免费分析工具 外贸人有句老话,七分靠选品,三分靠运营。在你开始做独立站之前,在你不清楚你的行业在Google上面能否有足够的流量时,那么Google Trends则是你最好的工具。 你只…...

【变频调速在锅炉引风机控制中的应用】
变频调速在锅炉引风机控制中的应用 变频器的选型 变频器是利用电力半导体器件的通断作用将工频电源变换为另一种频率的电能控制装置,能宏观对交流异步电机软启动,变频调速,提高运转精度,改变功率因数,过流/过压/过载保护等功能,国内技术较领先的品牌有汇川、欧瑞(原烟台…...
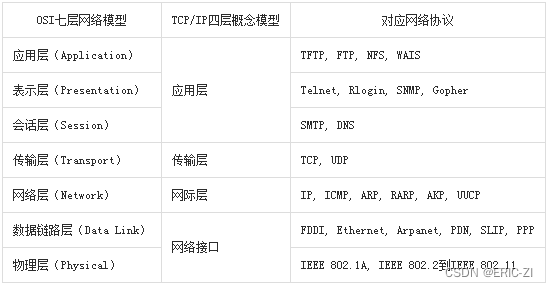
网络配置(IP、NETMASK、GATEWAY、DNS、DHCP) <持续更新中>
参考: 初学Linux之网络配置(IP、NETMASK、GATEWAY、DNS、DHCP)-CSDN博客【学习笔记】网关 & 路由_网关和路由-CSDN博客【学习笔记】计算机网络 IP地址与MAC地址_根据mac分配ip-CSDN博客【学习笔记】TCP 和 UDP 协议_tcp 发送 syn 应答没有syn ack-CSDN博客 一…...
【ArcGIS 脚本工具】拯救密恐,隐藏唯一值渲染图层的标记符号
最近拿到了【Hello 图狗】制作的三调/变更样式符号库,确实比之前网上下载的版本好用很多。 ArcGIS Pro三调23变更符号库V1.02(汇总)_中大比例尺.stylx和样式属性对调 不过使用过程中触发了一个旧病,就是匹配样式之后,…...

tensorflow学习1.3-创建会话,启动会话
tensorflow学习1.3-创建会话,启动会话 会话的由来与作用由来作用 会话的定义与结构定义 用法基本用法上下文管理器执行部分计算图获取多个结果 总结 练习代码报错原因:TensorFlow 2.x中的Eager Execution使用兼容模式来启用SessionEager Execution和计算…...
QT基本对话框(基本对话框、工具盒类、进度条、调色板与电子钟、可扩展对话框、程序启动画面)
此篇文章通过实例介绍基本对话框的用法。首先介绍标准文件对话框(QFileDialog)、标准颜色对话框(QColorDialog)、标准字体对话框(QFontDialog)、标准输入对话框(QInputDialog)以及标…...
Docker 部署 MariaDB 数据库 与 Adminer 数据库管理工具
文章目录 MariaDBmariadb.cnf开启 binlog Adminerdocker-compose.ymlAdminer 连接 MariaDB MariaDB MariaDB是一个流行的开源关系型数据库管理系统(RDBMS),它是MySQL的一个分支和替代品。 官网:https://mariadb.com/镜像ÿ…...

qt 可以在一个函数中读一个文件,然后再将内容写入另一个文件中
是的,Qt 允许你在一个函数中读取一个文件的内容,并将这些内容写入到另一个文件中。这可以通过结合使用 QFile 和 QTextStream(或 QDataStream,取决于你的具体需求)来实现。以下是一个简单的示例,展示了如何…...
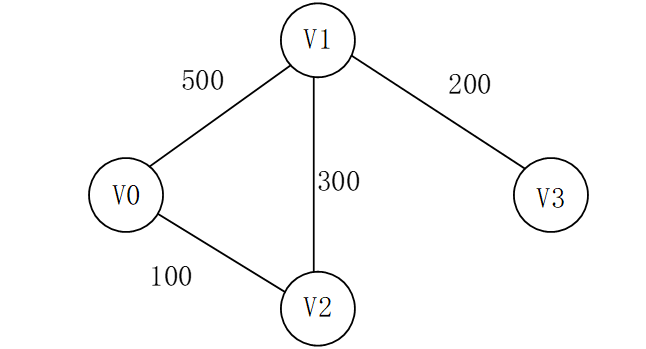
Dijkstra算法C代码
一个带权图n个点m条边,求起点到终点的最短距离 先定义一个邻接矩阵graph,graph[i][j]表示从i到j的距离,i到j没有路就表示为无穷 然后定义一个visit数组,visit[i]表示i结点是否被访问 然后定义一个dist数组,dist[i]表…...

P1064 [NOIP2006 提高组] 金明的预算方案
[NOIP2006 提高组] 金明的预算方案 题目描述 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置࿰…...

大型企业组网如何规划网络
大型企业组网是一个复杂的过程,它需要细致的规划和设计,以确保网络能够满足企业的业务需求,同时保证性能、安全性和可扩展性。以下是规划大型企业网络的一些关键步骤和考虑因素: 1. 需求分析 业务需求:与各个业务部门…...
)
java:aocache的单实例缓存(二)
之前一篇博客《java:aocache的单实例缓存》介绍了aoocache使用注解AoCacheable实现单实例缓存的方式,同时也指出了这种方式的使用限制,就是这个注解定义的构造方法,不能再创建出新实例。 为了更灵活方便的实现单实例。aocache最新版本0.4.0增…...
ElasticSearch安装部署
简介 Elasticsearch 是一个开源的分布式搜索和分析引擎,用于实时地存储、检索和分析大数据量。它基于 Apache Lucene 搜索引擎库构建而成,提供了一个强大、稳定且易于扩展的搜索解决方案。 主要特点和用途: 分布式存储和搜索: E…...
——开发:数据转换——影响因素、直接作用、主要特征)
数据赋能(132)——开发:数据转换——影响因素、直接作用、主要特征
影响因素 数据转换过程中需要考虑的一些影响因素: 数据格式与结构: 不同系统或应用可能使用不同的数据格式(如JSON、XML、CSV等)和数据结构(如关系型数据库、非关系型数据库等)。数据转换需要确保原始数据…...

TMGM:ASIC撤销禁令,TMGM强化合规、重启差价合约服务
TMGM作为差价合约(CFDs)与保证金外汇交易领域的领航者,安全、合规、高效被奉为我集团的终身使命。澳大利亚证券和投资委员会(ASIC)已正式撤销了早前针对TMGM差价合约业务实施的临时止损令。这一误会的解除,…...

基于SpringBoot网吧管理系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 Java精品实战案例《600套》 2025-2026年最值得选择的Java毕业设计选题大全࿱…...
实测2024年最佳的三款Socks5代理IP网站
一、引言 在浩瀚的网络世界中,Socks5代理IP服务如同导航灯塔,指引我们穿越数据海洋,安全、稳定地访问目标网站。作为专业的测评团队,我们深知一款优秀的Socks5代理IP网站需要具备哪些特质:稳定的IP资源、高效的连接速…...
Pythonnet能导入clr,但无法引入System模块?
【pythonnet详解】—— Python 和 .NET 互操作的库_pythonnet 详细使用-CSDN博客 Python中动态调用C#的dll动态链接库中方法_python 如何调用c# dll-CSDN博客 需求:Python调用并传List<float>类型参数给.Net 起初:直接 # 创建一个Python浮点数…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
