P1064 [NOIP2006 提高组] 金明的预算方案
[NOIP2006 提高组] 金明的预算方案
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 n n n 元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
| 主件 | 附件 |
|---|---|
| 电脑 | 打印机,扫描仪 |
| 书柜 | 图书 |
| 书桌 | 台灯,文具 |
| 工作椅 | 无 |
如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 0 0 0 个、 1 1 1 个或 2 2 2 个附件。每个附件对应一个主件,附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的 n n n 元。于是,他把每件物品规定了一个重要度,分为 5 5 5 等:用整数 1 ∼ 5 1 \sim 5 1∼5 表示,第 5 5 5 等最重要。他还从因特网上查到了每件物品的价格(都是 10 10 10 元的整数倍)。他希望在不超过 n n n 元的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 j j j 件物品的价格为 v j v_j vj,重要度为 w j w_j wj,共选中了 k k k 件物品,编号依次为 j 1 , j 2 , … , j k j_1,j_2,\dots,j_k j1,j2,…,jk,则所求的总和为:
v j 1 × w j 1 + v j 2 × w j 2 + ⋯ + v j k × w j k v_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k} vj1×wj1+vj2×wj2+⋯+vjk×wjk。
请你帮助金明设计一个满足要求的购物单。
输入格式
第一行有两个整数,分别表示总钱数 n n n 和希望购买的物品个数 m m m。
第 2 2 2 到第 ( m + 1 ) (m + 1) (m+1) 行,每行三个整数,第 ( i + 1 ) (i + 1) (i+1) 行的整数 v i v_i vi, p i p_i pi, q i q_i qi 分别表示第 i i i 件物品的价格、重要度以及它对应的的主件。如果 q i = 0 q_i=0 qi=0,表示该物品本身是主件。
输出格式
输出一行一个整数表示答案。
样例 #1
样例输入 #1
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
样例输出 #1
2200
提示
数据规模与约定
对于全部的测试点,保证 1 ≤ n ≤ 3.2 × 1 0 4 1 \leq n \leq 3.2 \times 10^4 1≤n≤3.2×104, 1 ≤ m ≤ 60 1 \leq m \leq 60 1≤m≤60, 0 ≤ v i ≤ 1 0 4 0 \leq v_i \leq 10^4 0≤vi≤104, 1 ≤ p i ≤ 5 1 \leq p_i \leq 5 1≤pi≤5, 0 ≤ q i ≤ m 0 \leq q_i \leq m 0≤qi≤m,答案不超过 2 × 1 0 5 2 \times 10^5 2×105。
NOIP 2006 提高组 第二题
这道题其实是一个背包问题和一个正常的dp转换问题,其实不难思考
首先我们可以想到在挑选一个主件时,可能会有四种情况:
情况1:只选主件
那么此时的状态转移方程就是
d p [ j ] = m a x ( d p [ j ] , d p [ j − w [ i ] ] + v [ i ] ) ; dp[j]=max(dp[j],dp[j-w[i]]+v[i]); dp[j]=max(dp[j],dp[j−w[i]]+v[i]);
情况2:只选主件和附件1
则可得到
d p [ j ] = m a x ( d p [ j ] , d p [ j − w [ i ] − f j w [ i ] [ 1 ] ] + v [ i ] + f j v [ i ] [ 1 ] ) ; dp[j]=max(dp[j],dp[j-w[i]-fjw[i][1]]+v[i]+fjv[i][1]); dp[j]=max(dp[j],dp[j−w[i]−fjw[i][1]]+v[i]+fjv[i][1]);
同样还有两种情况,会有以下的两种状态转移方程
d p [ j ] = m a x ( d p [ j ] , d p [ j − w [ i ] − f j w [ i ] [ 2 ] ] + v [ i ] + f j v [ i ] [ 2 ] ) ; dp[j]=max(dp[j],dp[j-w[i]-fjw[i][2]]+v[i]+fjv[i][2]); dp[j]=max(dp[j],dp[j−w[i]−fjw[i][2]]+v[i]+fjv[i][2]);
d p [ j ] = m a x ( d p [ j ] , d p [ j − w [ i ] − f j w [ i ] [ 1 ] − f j w [ i ] [ 2 ] ] + v [ i ] + f j v [ i ] [ 1 ] + f j v [ i ] [ 2 ] ) ; dp[j]=max(dp[j],dp[j-w[i]-fjw[i][1]-fjw[i][2]]+v[i]+fjv[i][1]+fjv[i][2]); dp[j]=max(dp[j],dp[j−w[i]−fjw[i][1]−fjw[i][2]]+v[i]+fjv[i][1]+fjv[i][2]);
既然有了此,那么程序就好写了
#include <bits/stdc++.h>
using namespace std;int n,m;
int v[32100],w[32100],fjw[32100][3],fjv[32100][3];//v为主件的价值,w为主件的重量,fjw为附件的重量,fjv为附件的价值
int dp[33300];
int main() {cin>>n>>m;for (int i=1;i<=m;i++){int a,b,c;cin>>a>>b>>c;if (c==0){v[i]=a*b;w[i]=a;}else {fjw[c][0]++;fjw[c][fjw[c][0]]=a;fjv[c][fjw[c][0]]=a*b;}}for (int i=1;i<=m;i++){for (int j=n;j>=w[i];j--){dp[j]=max(dp[j],dp[j-w[i]]+v[i]);//情况1只要主件if (j>=w[i]+fjw[i][1])dp[j]=max(dp[j],dp[j-w[i]-fjw[i][1]]+v[i]+fjv[i][1]);//情况2只要主件和附件1if (j>=w[i]+fjw[i][2])dp[j]=max(dp[j],dp[j-w[i]-fjw[i][2]]+v[i]+fjv[i][2]);//情况2只要主件和附件2if (j>=w[i]+fjw[i][1]+fjw[i][2])dp[j]=max(dp[j],dp[j-w[i]-fjw[i][1]-fjw[i][2]]+v[i]+fjv[i][1]+fjv[i][2]);//情况3都要}}cout<<dp[n];return 0;
}
相关文章:

P1064 [NOIP2006 提高组] 金明的预算方案
[NOIP2006 提高组] 金明的预算方案 题目描述 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置࿰…...

大型企业组网如何规划网络
大型企业组网是一个复杂的过程,它需要细致的规划和设计,以确保网络能够满足企业的业务需求,同时保证性能、安全性和可扩展性。以下是规划大型企业网络的一些关键步骤和考虑因素: 1. 需求分析 业务需求:与各个业务部门…...
)
java:aocache的单实例缓存(二)
之前一篇博客《java:aocache的单实例缓存》介绍了aoocache使用注解AoCacheable实现单实例缓存的方式,同时也指出了这种方式的使用限制,就是这个注解定义的构造方法,不能再创建出新实例。 为了更灵活方便的实现单实例。aocache最新版本0.4.0增…...
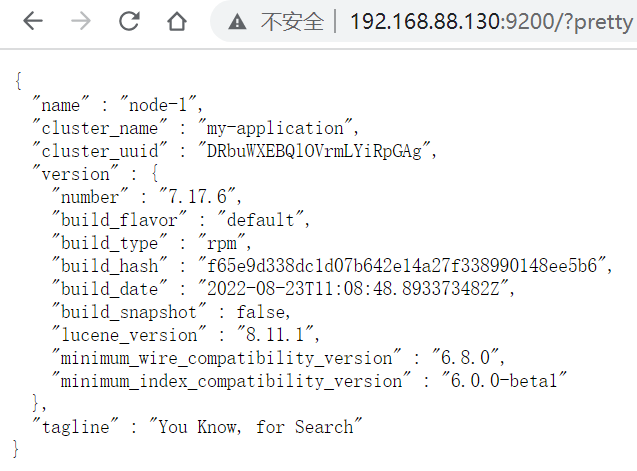
ElasticSearch安装部署
简介 Elasticsearch 是一个开源的分布式搜索和分析引擎,用于实时地存储、检索和分析大数据量。它基于 Apache Lucene 搜索引擎库构建而成,提供了一个强大、稳定且易于扩展的搜索解决方案。 主要特点和用途: 分布式存储和搜索: E…...
——开发:数据转换——影响因素、直接作用、主要特征)
数据赋能(132)——开发:数据转换——影响因素、直接作用、主要特征
影响因素 数据转换过程中需要考虑的一些影响因素: 数据格式与结构: 不同系统或应用可能使用不同的数据格式(如JSON、XML、CSV等)和数据结构(如关系型数据库、非关系型数据库等)。数据转换需要确保原始数据…...

TMGM:ASIC撤销禁令,TMGM强化合规、重启差价合约服务
TMGM作为差价合约(CFDs)与保证金外汇交易领域的领航者,安全、合规、高效被奉为我集团的终身使命。澳大利亚证券和投资委员会(ASIC)已正式撤销了早前针对TMGM差价合约业务实施的临时止损令。这一误会的解除,…...

基于SpringBoot网吧管理系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 Java精品实战案例《600套》 2025-2026年最值得选择的Java毕业设计选题大全࿱…...
实测2024年最佳的三款Socks5代理IP网站
一、引言 在浩瀚的网络世界中,Socks5代理IP服务如同导航灯塔,指引我们穿越数据海洋,安全、稳定地访问目标网站。作为专业的测评团队,我们深知一款优秀的Socks5代理IP网站需要具备哪些特质:稳定的IP资源、高效的连接速…...
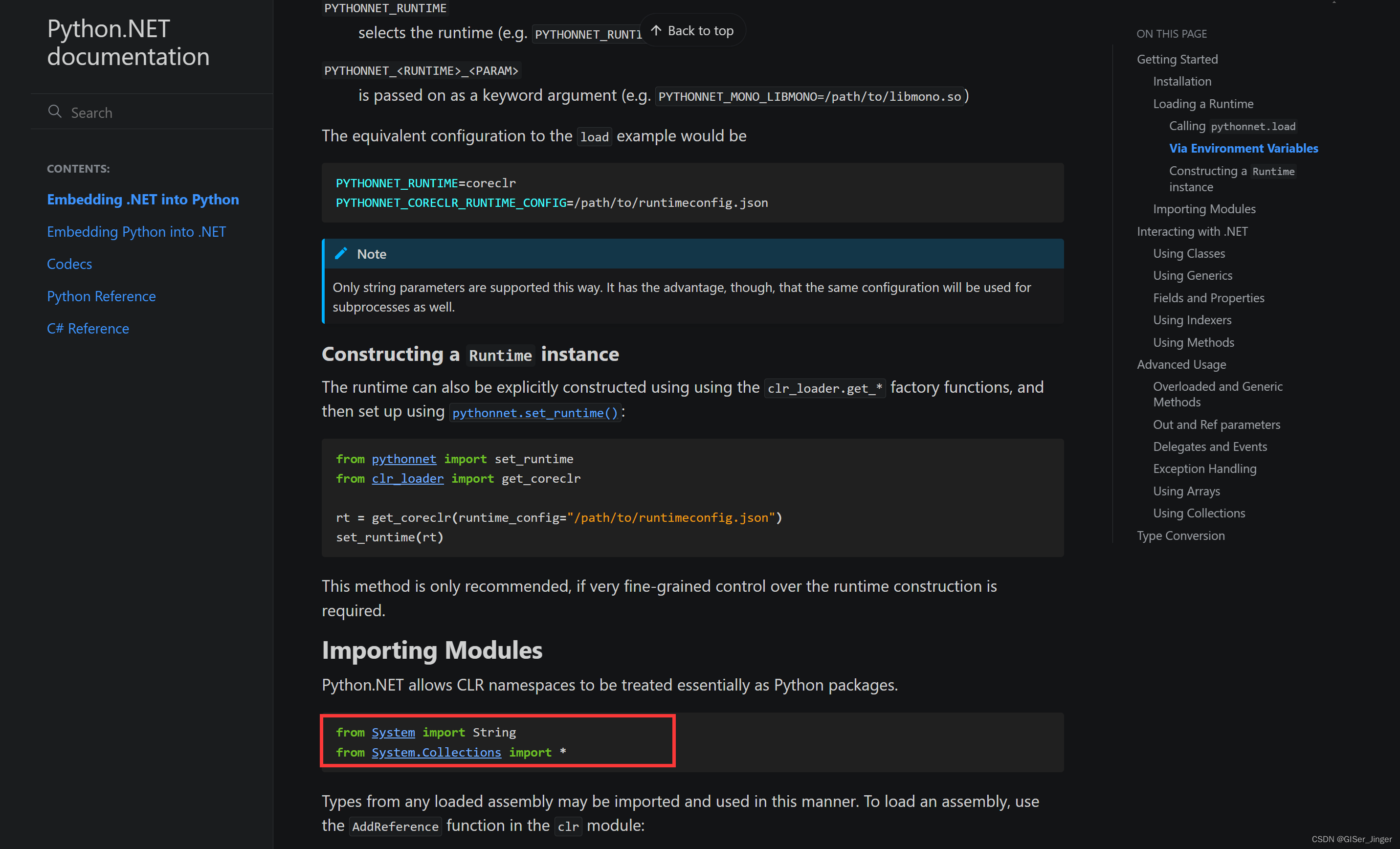
Pythonnet能导入clr,但无法引入System模块?
【pythonnet详解】—— Python 和 .NET 互操作的库_pythonnet 详细使用-CSDN博客 Python中动态调用C#的dll动态链接库中方法_python 如何调用c# dll-CSDN博客 需求:Python调用并传List<float>类型参数给.Net 起初:直接 # 创建一个Python浮点数…...

媒体宣发套餐的概述及推广方法-华媒舍
在今天的数字化时代,对于产品和服务的宣传已经变得不可或缺。媒体宣发套餐作为一种高效的宣传方式,在帮助企业塑造品牌形象、扩大影响力方面扮演着重要角色。本文将揭秘媒体宣发套餐,为您呈现一条通往成功的路。 1. 媒体宣发套餐的概述 媒体…...
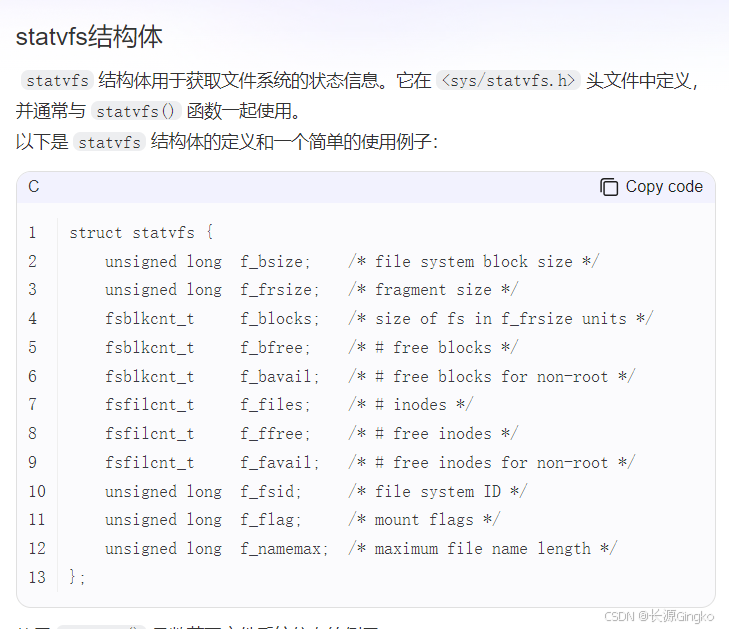
Windows和Linux C++判断磁盘空间是否充足
基本是由百度Ai写代码生成的,记录一下。实现此功能需要调用系统的API函数。 对于Windows,可调用函数GetDiskFreeSpaceEx,使用该函数需要包含头文件windows.h。该函数的原型: 它的四个参数: lpDirectoryName࿰…...

数据访问层如何提取数据到其他层,其他类中
当然可以,以下是一些具体的例子,展示了如何将数据库访问逻辑封装在一个单独的类中,并在其他类中使用这个类来获取数据。 数据库访问类(DatabaseAccess.java): java复制代码 import java.sql.*; import ja…...

【JS】AI总结:JavaScript中常用的判空方法
在JavaScript中,判空是一个常见的操作,因为变量可能未定义、未初始化或包含特定的空值。以下是JavaScript中常用的判空方法: 使用if语句直接判断: 如果变量是null、undefined、0、NaN、空字符串(""ÿ…...
Rust单元测试、集成测试
单元测试、集成测试 在了解了如何在 Rust 中写测试用例后,本章节我们将学习如何实现单元测试、集成测试,其实它们用到的技术还是上一章节中的测试技术,只不过对如何组织测试代码提出了新的要求。 单元测试 单元测试目标是测试某一个代码单…...
vue全局方法plugins/utils
一、在src目录下创建一个plugins文件夹 test.ts文件存放创建的方法,index.ts用于接收所有自定义方法进行统一处理 二、编写自定义方法 // test.ts文件 export default {handleTest(val1: number, val2: number) {// 只是一个求和的方法return val1 val2;}, };三…...

高阶算法班从入门到精通之路
课程介绍 本课程旨在帮助学员深入理解算法与数据结构的核心概念,从而掌握高级算法设计与分析技能。每集课程内容精心设计,涵盖了常用数据结构、经典算法及其应用场景等方面的深度讲解,同时通过大量实例演练,帮助学员提升解决实际…...

C++ 左值右值
文章目录 概述左值右值右值引用左值和右值的互换 小结 概述 左值和右值属于2中不同的表达式类型;它们在表达式中扮演不同的角色,特别是在赋值操作和函数参数传递中。 左值 定义:左值是指那些在内存中有确定位置的表达式,可以出…...
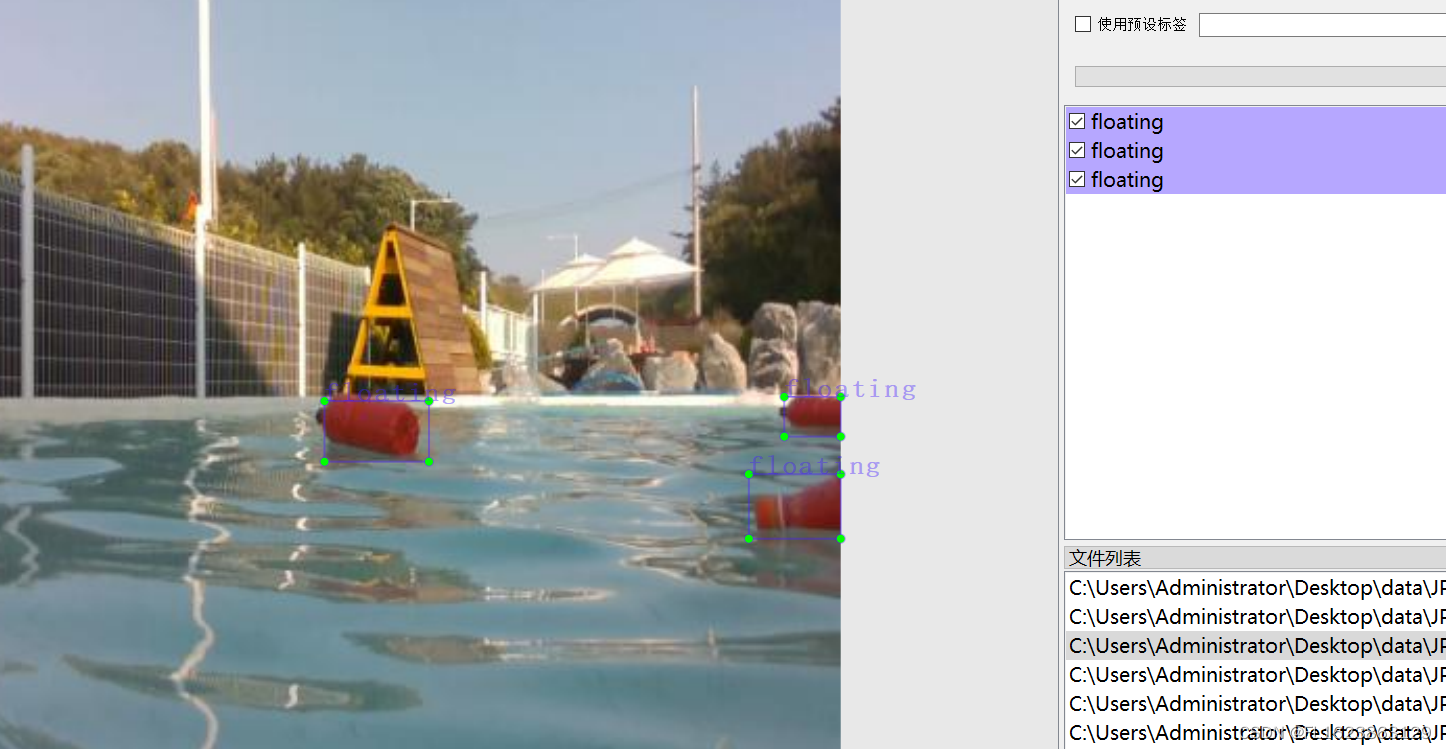
[数据集][目标检测]水面垃圾水面漂浮物检测数据集VOC+YOLO格式3749张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):3749 标注数量(xml文件个数):3749 标注数量(txt文件个数):3749 标注…...
[深度学习] 卷积神经网络CNN
卷积神经网络(Convolutional Neural Network, CNN)是一种专门用于处理数据具有类似网格结构的神经网络,最常用于图像数据处理。 一、CNN的详细过程: 1. 输入层 输入层接收原始数据,例如一张图像,它可以被…...

区别QPushButton和QToolButton
在刚开始学习Qt时,可能很难理解QPushButton和QToolButton之间的区别。 QToolButton通常用于QToolBar中,常常只显示图标,而不显示文本。那么,它们的主要区别是什么?什么时候应该使用QPushButton,什么时候应该使用QToolButton? 了解这一点很重要,这样我们才能选择最合适…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...

Python网页自动化测试,DrissonPage库入门说明文档
🛰️ 基本逻辑 操作浏览器的基本逻辑如下: 创建浏览器对象,用于启动或接管浏览器获取一个 Tab 对象使用 Tab 对象访问网址使用 Tab 对象获取标签页内需要的元素对象使用元素对象进行交互 除此以外,还能执行更为复杂的操作&am…...
