14 卡尔曼滤波及代码实现
文章目录
- 14 卡尔曼滤波及代码实现
- 14.0 基本概念
- 14.1 公式推导
- 14.2 代码实现
14 卡尔曼滤波及代码实现
14.0 基本概念
卡尔曼滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
通俗来说就是,线性数学模型算出预测值+传感器测量值=更准确的测量值。根据数学模型,由第 k k k 时刻的值递推得到第 k + 1 k+1 k+1 时刻的预测值,结合第 k + 1 k+1 k+1 时刻的观测值,得到第 k + 1 k+1 k+1 时刻更精准的值。
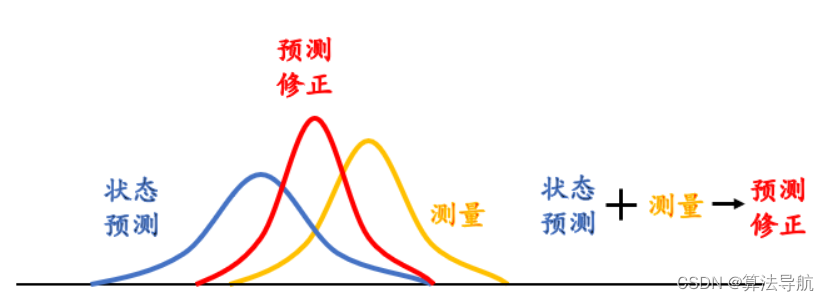
卡尔曼滤波主要用于 线性高斯系统。
14.1 公式推导
(1)线性高斯系统表达
状态方程:
x k = A x k − 1 + B u k + w k \boldsymbol{x}_k = \boldsymbol{A}\boldsymbol{x}_{k-1}+\boldsymbol{B}\boldsymbol{u}_k+\boldsymbol{w}_k xk=Axk−1+Buk+wk
观测方程:
z k = H x k + v k \boldsymbol{z}_k = \boldsymbol{H}\boldsymbol{x}_k+\boldsymbol{v}_k zk=Hxk+vk
其中, x k \boldsymbol{x}_k xk 为状态量, z k \boldsymbol{z}_k zk 为观测量, A \boldsymbol{A} A 为状态转移矩阵, B k \boldsymbol{B}_k Bk 为控制输入矩阵, H \boldsymbol{H} H 为状态观测矩阵。
w k \boldsymbol{w}_k wk 是过程噪声,服从高斯分布, w k \boldsymbol{w}_k wk 是观测噪声,也服从高斯分布,即:
w k ∼ N ( 0 , Q ) \boldsymbol{w}_k \sim N(0, \boldsymbol{Q}) wk∼N(0,Q)
v k ∼ N ( 0 , R ) \boldsymbol{v}_k \sim N(0, \boldsymbol{R}) vk∼N(0,R)
其中 Q \boldsymbol{Q} Q 是过程噪声的协方差, R \boldsymbol{R} R 是观测噪声的协方差。
卡尔曼滤波包括预测和更新两步。
(2)预测(先验)
预测是根据上一时刻的状态量,由状态方程预测出下一时刻的状态量 x ^ k − \hat{\boldsymbol{x}}_k^{-} x^k− ,以及状态量误差协方差的先验估计矩阵 P k − \boldsymbol{P}_k^{-} Pk−。这是没有加观测值的。
x ^ k − = A x ^ k − 1 + B u k \hat{\boldsymbol{x}}_k^{-} = \boldsymbol{A}\hat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}\boldsymbol{u}_k x^k−=Ax^k−1+Buk
P k − = A P k − 1 A T + Q \boldsymbol{P}_k^{-}=\boldsymbol{AP}_{k-1}\boldsymbol{A}^T+\boldsymbol{Q} Pk−=APk−1AT+Q
其中, A x ^ k − 1 \boldsymbol{A}\hat{\boldsymbol{x}}_{k-1} Ax^k−1 是上一时刻的最优估计。
(3)更新(后验)
加入观测,对预测值进行更新校正,得到最优后验估计。
首先计算增益矩阵
K k = P k − H T ( H P k − H T + R ) − 1 \boldsymbol{K}_k=\boldsymbol{P}_k^{-}\boldsymbol{H}^T(\boldsymbol{H}\boldsymbol{P}_k^{-}\boldsymbol{H}^T+\boldsymbol{R})^{-1} Kk=Pk−HT(HPk−HT+R)−1
更新状态量及其协方差矩阵
x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{\boldsymbol{x}}_k = \hat{\boldsymbol{x}}_k^{-} + \boldsymbol{K}_k(\boldsymbol{z}_k-\boldsymbol{H}\hat{\boldsymbol{x}}_k^{-}) x^k=x^k−+Kk(zk−Hx^k−)
P k = ( I − K k H ) P k − \boldsymbol{P}_k=(\boldsymbol{I}-\boldsymbol{K}_k\boldsymbol{H})\boldsymbol{P}_k^{-} Pk=(I−KkH)Pk−
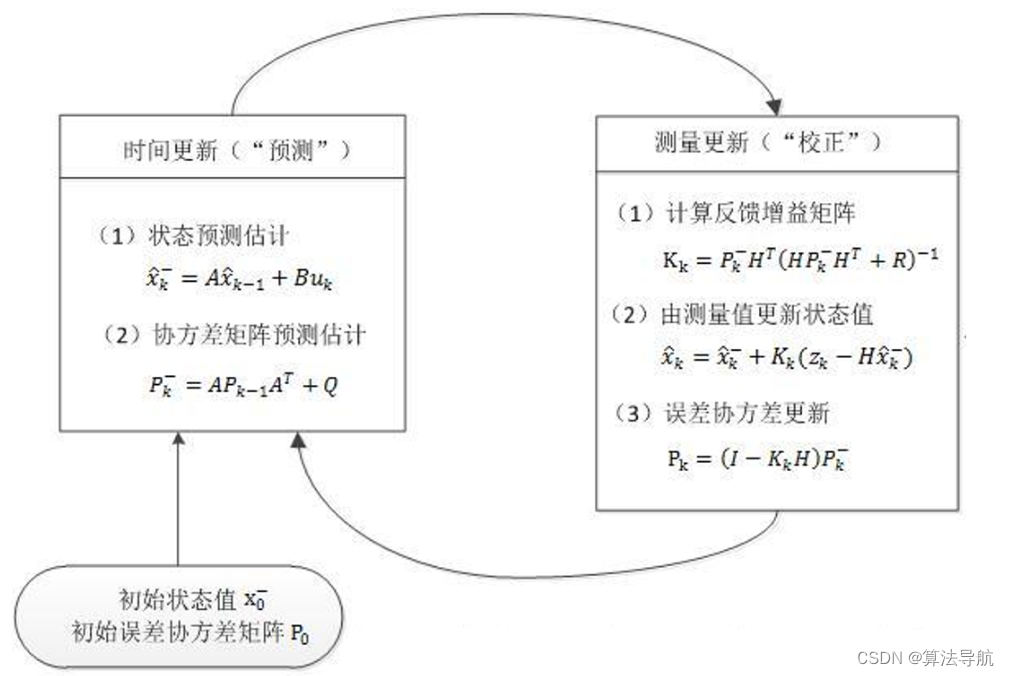
14.2 代码实现
以雷达追踪目标为背景,系统的状态方程为
[ x y V x V y a x a y ] k + 1 = [ 1 0 δ t 0 0.5 δ t 2 0 0 1 0 δ t 0 0.5 δ t 2 0 0 1 0 δ t 0 1 0 0 1 0 δ t 0 0 0 0 1 0 0 0 0 1 0 1 ] [ x y V x V y a x a y ] k \begin{bmatrix}x\\y\\Vx\\Vy\\ax\\ay\end{bmatrix}_{k+1}=\begin{bmatrix}1&0&\delta_t&0&0.5\delta_t^2&0\\0&1&0&\delta_t&0&0.5\delta_t^2\\0&0&1&0&\delta_t&0\\1&0&0&1&0&\delta_t\\0&0&0&0&1&0\\0&0&0&1&0&1\end{bmatrix}\begin{bmatrix}x\\y\\Vx\\Vy\\ax\\ay\end{bmatrix}_k xyVxVyaxay k+1= 100100010000δt010000δt01010.5δt20δt01000.5δt20δt01 xyVxVyaxay k
观测方程
[ x y ] k + 1 = [ 1 0 0 0 0 0 0 1 0 0 0 0 ] [ x y V x V y a x a y ] k \begin{bmatrix}x\\y\end{bmatrix}_{k+1}=\begin{bmatrix}1&0&0&0&0&0\\0&1&0&0&0&0\end{bmatrix}\begin{bmatrix}x\\y\\Vx\\Vy\\ax\\ay\end{bmatrix}_k [xy]k+1=[100100000000] xyVxVyaxay k
/*********************************************************** *
* Time: 2023/11/26
* Author: xiaocong
* Function: 卡尔曼滤波
***********************************************************/
#ifndef KALMANFILTER_H
#define KALMANFILTER_H#include <eigen3/Eigen/Dense>
#include <iostream>using namespace Eigen;
using namespace std;class KalmanFilter
{
public:KalmanFilter(int stateSize, int measSize, int uSize); // 构造函数void init(VectorXd& x, MatrixXd& P, MatrixXd& R, MatrixXd& Q); // 初始化void predict(MatrixXd& A);void predict(MatrixXd& A, MatrixXd& B, VectorXd& u); // 重载,针对有控制输入的情况VectorXd update(MatrixXd& H, VectorXd z_meas); // 更新~KalmanFilter(); // 析构函数private:VectorXd x_; // 状态变量VectorXd z_; // 观测变量MatrixXd A_; // 状态转移矩阵MatrixXd B_; // 控制矩阵VectorXd u_; // 控制变量MatrixXd P_; // 状态值的协方差矩阵MatrixXd H_; // 观测矩阵MatrixXd R_; // 观测噪声协方差矩阵MatrixXd Q_; // 过程噪声协方差矩阵
};#endif //KALMANFILTER_H
#include "../inlude/KalmanFilter.h"// 构造函数
KalmanFilter::KalmanFilter(int stateSize, int measSize, int uSize)
{if (stateSize == 0 || measSize == 0){std::cerr << "Error, State size and measurement size must bigger than 0" << endl;}x_.resize(stateSize);x_.setZero();A_.resize(stateSize, stateSize);A_.setIdentity();u_.resize(uSize);u_.setZero();B_.resize(stateSize, uSize);B_.setZero();P_.resize(stateSize, stateSize);P_.setIdentity();H_.resize(measSize, stateSize);H_.setZero();Q_.resize(stateSize, stateSize);Q_.setIdentity();R_.resize(measSize, measSize);R_.setIdentity();
}void KalmanFilter::init(VectorXd& x, MatrixXd& P, MatrixXd& R, MatrixXd& Q)
{x_ = x;P_ = P;R_ = R;Q_ = Q;
}void KalmanFilter::predict(MatrixXd& A) // 没有控制输入u
{A_ = A;x_ = A * x_;P_ = A_ * P_ * A_.transpose() + Q_;
}void KalmanFilter::predict(MatrixXd& A, MatrixXd& B, VectorXd& u) // 有控制输入u
{A_ = A;B_ = B;u_ = u;x_ = A * x_ + B * u_;P_ = A_ * P_ * A_.transpose() + Q_;
}VectorXd KalmanFilter::update(MatrixXd& H, VectorXd z_meas) // 更新
{H_ = H;MatrixXd temp = H_ * P_ * H_.transpose() + R_;MatrixXd K = P_ * H_.transpose() * temp.inverse();x_ = x_ + K * (z_meas - H_ * x_); // 更新 x_kMatrixXd I = MatrixXd::Identity(x_.rows(), x_.rows());P_ = (I - K * H_) * P_;return x_;
}KalmanFilter::~KalmanFilter()
{}
#include "../inlude/KalmanFilter.h"
#include <fstream>#define N 1000
#define T 0.01double data_x[N], data_y[N];// 模型函数
double sample(double x0, double v0, double acc, double t)
{return x0 + v0 * t + 0.5 * acc * t * t;
}double getRand()
{return 0.5 * rand() / RAND_MAX - 0.25; //[-0.25, 0.25)
}int main()
{ofstream fout;fout.open("../data/data.txt");// 生成观测值double t;for (int i = 0; i < N; i++){t = T * i;data_x[i] = sample(0, -4.0, 0.1, t) + getRand();data_y[i] = sample(0.1, 2.0, 0, t) + getRand();}int stateSize = 6;int measSize = 2;int uSize = 0;KalmanFilter kf(stateSize, measSize, uSize);Eigen::MatrixXd A(stateSize, stateSize);A << 1, 0, T, 0, 1 / 2 * T * T, 0,0, 1, 0, T, 0, 1 / 2 * T * T,0, 0, 1, 0, T, 0,0, 0, 0, 1, 0, T,0, 0, 0, 0, 1, 0,0, 0, 0, 0, 0, 1;Eigen::MatrixXd B(0, 0);Eigen::MatrixXd H(measSize, stateSize);H << 1, 0, 0, 0, 0, 0,0, 1, 0, 0, 0, 0;Eigen::MatrixXd P(stateSize, stateSize);P.setIdentity();Eigen::MatrixXd R(measSize, measSize);R.setIdentity() * 0.01;Eigen::MatrixXd Q(stateSize, stateSize);Q.setIdentity() * 0.001;Eigen::VectorXd x(stateSize);Eigen::VectorXd u(0);Eigen::VectorXd z_meas(measSize);z_meas.setZero();Eigen::VectorXd res(stateSize); // 存储预测结果for (int i = 0; i < N; i++){if (i == 0) // 初始值{x << data_x[i], data_y[i], 0, 0, 0, 0;kf.init(x, P, R, Q);continue;}kf.predict(A); // 预测z_meas << data_x[i], data_y[i]; // 观测res << kf.update(H, z_meas); // 更新fout << data_x[i] << " " << data_y[i] << " " << res[0] << " " << res[1] << " " << res[2] << " " << res[3] << " " << res[4] << " " << res[5] << endl;}fout.close();return 0;}
相关文章:

14 卡尔曼滤波及代码实现
文章目录 14 卡尔曼滤波及代码实现14.0 基本概念14.1 公式推导14.2 代码实现 14 卡尔曼滤波及代码实现 14.0 基本概念 卡尔曼滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据包括系统中的噪声和…...
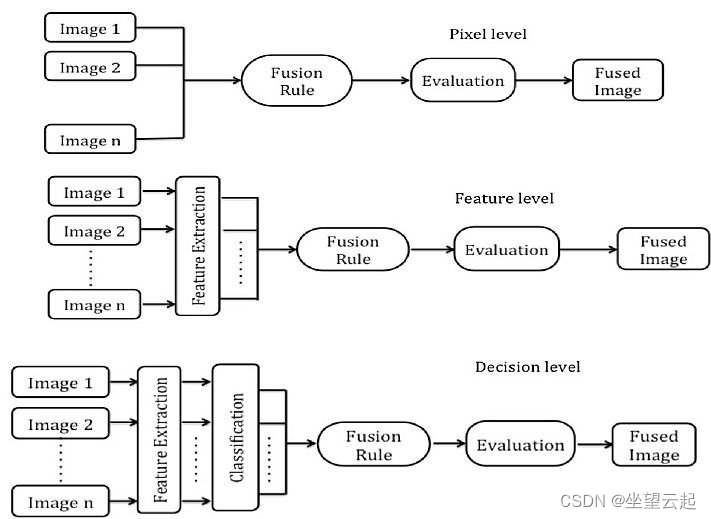
计算机视觉 图像融合技术概览
在许多计算机视觉应用中(例如机器人运动和医学成像),需要将来自多幅图像的相关信息集成到一幅图像中。这种图像融合将提供更高的可靠性、准确性和数据质量。 多视图融合可以提高图像的分辨率,同时恢复场景的 3D 表示。多模态融合结合了来自不同传感器的图像,称为多传感器融…...
计算机网络课程实训:局域网方案设计与实现(基于ensp)
文章目录 前言基本要求操作分公司1分公司2总部核心交换机配置实现内部服务器的搭建acl_deny部分用户与服务器出口出口防火墙配置 前言 本篇文章是小编实训部分内容,内容可能会有错误,另外ensp对电脑兼容性及其挑剔,在使用之前一定要安装好。…...
【安全开发】内网扫描器
文章目录 前言现实现的功能较少后序开发会逐步加入简单漏洞探探测和代理功能。 一、开发过程1.项目结构2.main.go3.core模块3.1 scanner.go3.2 service.go 4.bruteforc4.1 bruteforce.go 二、使用步骤 前言 为什么要写这个? fscna被杀的概率太高(哪天二…...
)
ESP32-C3模组上跑通MQTT(5)
接前一篇文章:ESP32-C3模组上跑通MQTT(4) 本文内容参考: 《ESP32-C3 物联网工程开发实战》 一分钟了解MQTT协议 ESP32 MQTT API指南-CSDN博客 ESP-IDF MQTT 示例入门_mqtt outbox-CSDN博客 ESP32用自签CA进行MQTT的TLS双向认证通信_esp32 mqtt ssl-CSDN博客 特此致谢!…...
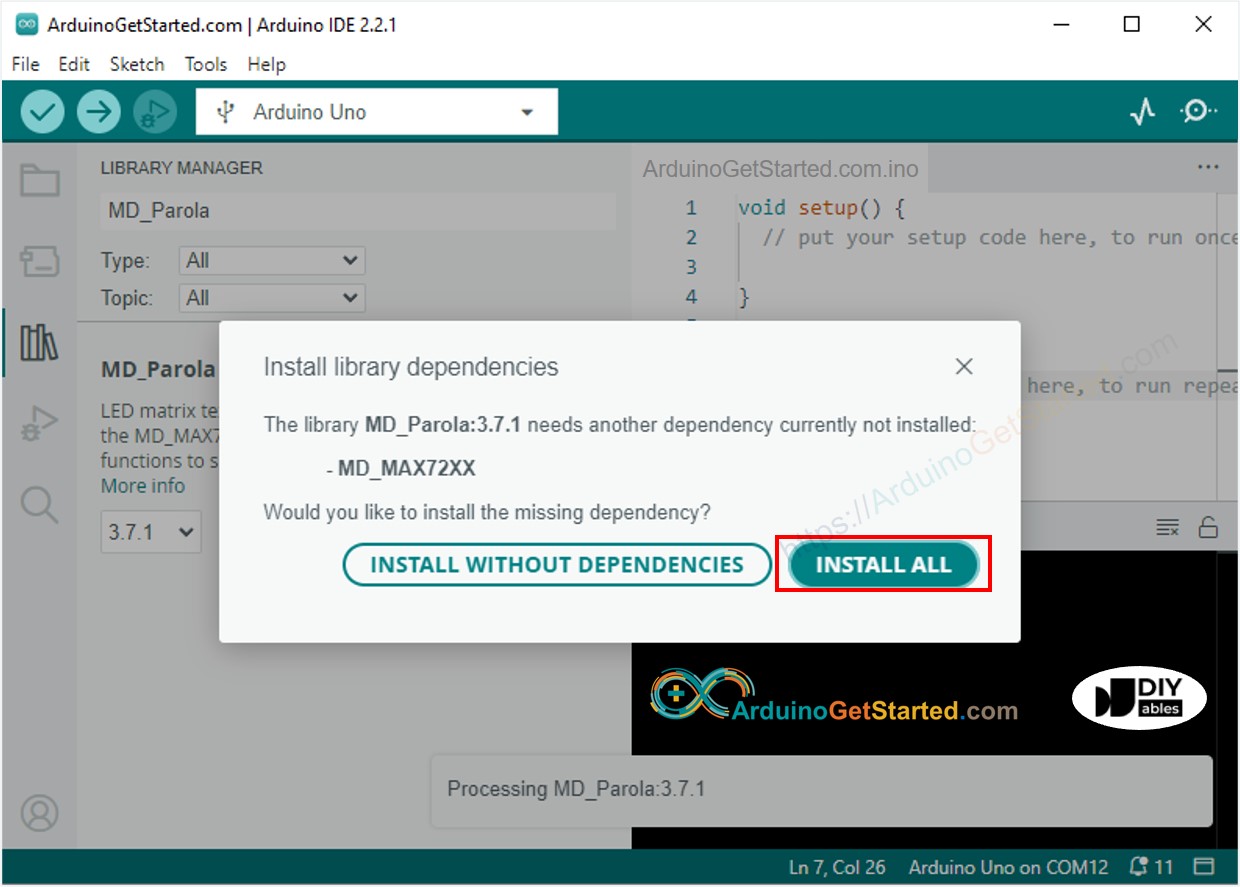
Arduino - LED 矩阵
Arduino - LED 矩阵 Arduino - LED Matrix LED matrix display, also known as LED display, or dot matrix display, are wide-used. In this tutorial, we are going to learn: LED矩阵显示器,也称为LED显示器,或点阵显示器,应用广泛。在…...
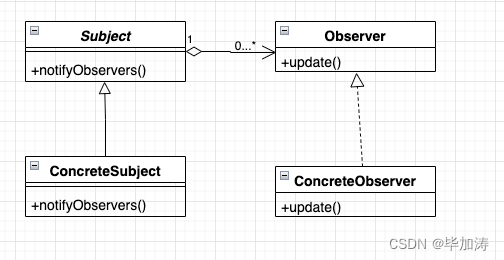
设计模式 - Observer Pattern 观察者模式
文章目录 定义观察者模式的实现构成构成UML图 观察者模式的代码实现场景代码实现 总结优点缺点应用场景 其他设计模式文章: 定义 观察者模式是行为型模式的一种,它定义对象间的一种一对多的依赖关系,使得每当一个对象改变状态,它…...

【面试系列】C++ 高频面试题
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题. ⭐️ AIGC时代的创新与未来:详细讲解AIGC的概念、核心技术、…...

程序猿大战Python——实现简单的图书馆系统操作
步骤1:安装和导入库 首先,确保已经安装了 pymysql 库。如果没有安装,请执行以下命令: pip install pymysql 然后,导入必要的库: import pymysql 步骤2:创建数据库和表的函数 编写一个函数来…...

液体粒子计数器的原理及常见型号选择 lighthouse代理商北京中邦兴业
液体颗粒计数用于测量液体样品中颗粒的大小和分布。通过用激光二极管照射液体样品并检测散射光来测量颗粒分布和尺寸。散射光的性质与粒子大小的大小有关。液体颗粒计数器可用于批量取样或在线(连续监测)应用,如水处理厂,或用于…...

Java知识点整理 16 — Spring Bean
在之前的文章 Java知识点整理 8 — Spring 简介 中介绍了 Spring 的两大核心概念 IoC 和 AOP,但对 Spring Bean 的介绍不全面,本文将补充 Spring 中 Bean 的概念。 一. 什么是 Spring Bean 在 Spring 官方文档中,对 bean 的定义为…...

Nvidia Jetson/RK3588+AI双目立体相机,适合各种割草机器人、扫地机器人、AGV等应用
双目立体视觉是基于视差原理,依据成像设备从不同位置获取的被测物体的图像,匹配对应点的位置偏移,得到视差数据,进而计算物体的空间三维信息。为您带来高图像质量的双目立体相机,具有高分辨率、低功耗、远距离等优点&a…...

springboot使用feign调用不依赖cloud
在使用spring boot调用第三方api中,常用的是okhttp、apache http client等,但是直接使用下来还是有点繁琐,需要手动转换实体。 在springcloud中有个openfeign调用,第一次体验到调用接口还能这么丝滑。注解写道接口上,…...
springboot中使用springboot cache
前言:SpringBoot中使用Cache缓存可以提高对缓存的开发效率 此图片是SpringBootCache常用注解 Springboot Cache中常用注解 第一步:引入依赖 <!--缓存--><dependency><groupId>org.springframework.boot</groupId><artifactId…...

Promise,async/await的运用
一,了解Promise Promise是异步编程的一种解决方案,它是一个对象,可以获取异步操作的消息,它的出现避免了地狱回调。 (1)Promise的实例有三个状态: Pending(进行中) Re…...

图论·多源最短路径Floyddijsktra
例题地址 多源最短路径 多个源点多个终点可以使用Floyd算法直接求各源点到终点的最短距离,也可以直接多次使用dijsktra算法求单源点到终点的最短距离 Floyd算法 使用条件 多源最短路径权值正负皆可 核心思想:动态规划 子问题: 设(A,B)…...
微服务 | Springboot整合GateWay+Nacos实现动态路由
1、简介 路由转发 执行过滤器链。 网关,旨在为微服务架构提供一种简单有效的统一的API路由管理方式。同时,基于Filter链的方式提供了网关的基本功能,比如:鉴权、流量控制、熔断、路径重写、黑白名单、日志监控等。 基本功能…...

做google SEO 有哪些好用的工具?这12款谷歌SEO工具值得收藏!
1、Google Trends 谷歌旗下一款基于搜索数据推出的一款免费分析工具 外贸人有句老话,七分靠选品,三分靠运营。在你开始做独立站之前,在你不清楚你的行业在Google上面能否有足够的流量时,那么Google Trends则是你最好的工具。 你只…...

【变频调速在锅炉引风机控制中的应用】
变频调速在锅炉引风机控制中的应用 变频器的选型 变频器是利用电力半导体器件的通断作用将工频电源变换为另一种频率的电能控制装置,能宏观对交流异步电机软启动,变频调速,提高运转精度,改变功率因数,过流/过压/过载保护等功能,国内技术较领先的品牌有汇川、欧瑞(原烟台…...
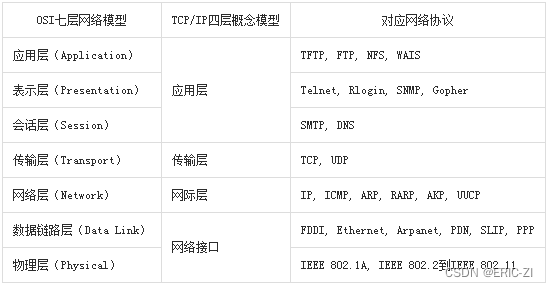
网络配置(IP、NETMASK、GATEWAY、DNS、DHCP) <持续更新中>
参考: 初学Linux之网络配置(IP、NETMASK、GATEWAY、DNS、DHCP)-CSDN博客【学习笔记】网关 & 路由_网关和路由-CSDN博客【学习笔记】计算机网络 IP地址与MAC地址_根据mac分配ip-CSDN博客【学习笔记】TCP 和 UDP 协议_tcp 发送 syn 应答没有syn ack-CSDN博客 一…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

机器学习复习3--模型评估
误差与过拟合 我们将学习器对样本的实际预测结果与样本的真实值之间的差异称为:误差(error)。 误差定义: ①在训练集上的误差称为训练误差(training error)或经验误差(empirical error&#x…...
