强化学习专题：强化学习知识梳理（一）

2024/6/23：

        前段时间有幸完成了大学期间的第一篇论文。在面试之前复盘一下关于自己论文中DQN的一些相关点。

浅谈主要区别（在线 or 离线）

        首先，一切的开始是强化学习中时序差分方程，这体现了强化学习方法的优化策略。在看方程之前，先要理解Q值的概念——即当前状态S下采取动作A继续下去能够得到的最佳收益。

        该方程通过Target值（采取当前动作后得到的奖励 + 采取动作后下一个状态根据某个策略选取动作的Q值）减去估计值（当前估计的当前状态采取A的Q值）再乘上一个类似于学习率的量来更新当前估计的当前状态的Q值，而方程的目的就是来逼近真正的最佳收益。可能有点绕，但是从类似于动态规划的角度看会明白一点。

        下面是on-policy和off-policy策略的区别：

        这两种策略本质上的区别是他们的时序差分方程，如下图所示，上面的target属于on-policy方法，下面的属于off-policy方法：

        on-policy主要应用于Sarsa方法，是一种在线的交互式的学习方法，大概就像是。采取这种策略的方法通过当前状态下选取的一定会执行的action来优化自身的Q表格。action的选取可以通过随机选取，也可以根据贪婪策略选取，然后根据这个选取的action计算得到的结果来更新Q表格。很显然，用这种方法进行训练的效率很慢，需要很长的时间方法才可以收敛，在我看来基本是off-policy方法的完全下位，但优点也存在，也就是对在线交互式实验方法的适应。

        从时序差分方程的角度看下面这张图，将其中的内容和方程中的联系起来看，就能大概理解sarsa做了什么：

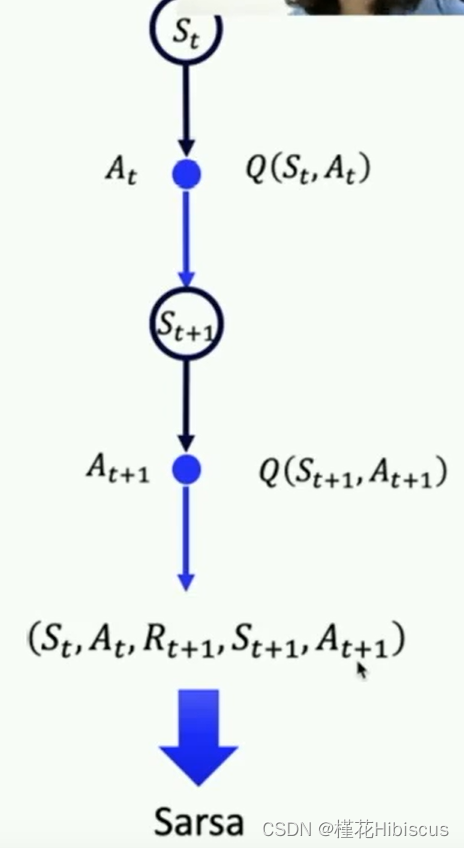
        off-policy是一种更加常用的方法，Q-learning和DQN都属于这一类的方法。从方程中获取target值的区别就可以看到，他使用下个状态的采取所有动作的最佳Q值来优化，因此收敛也更快。

参考：在线/离线策略区别

面向新手：从零学习强化学习