React实战学习(一)_棋盘设计

需求:
- 左上侧:状态
- 左下侧:棋盘,保证胜利就结束 和 下过来的不能在下
- 右侧:“时光机”,保证可以回顾,索引
语法:
- 父子之间属性传递(props)
- 子父组件传递(写法上!回调函数,若与前者相同会出现无限渲染)
//父组件中声明<Square value={squares[0]} onSquareClick={() => handleClick(0)} /> //子组件接收或发射function Square({ value, onSquareClick }) {return (<button className="square" onClick={onSquareClick}>{value}</button>); }
Idea 时光机:
- 不改动原数组,slice()拷贝原数组,[...history,squares]存各个时间数据
- 若与每一步索引有关,[...history.slice(0, currentMove + 1), nextSquares]
import { useState } from 'react';function Square({ value, onSquareClick }) {return (<button className="square" onClick={onSquareClick}>{value}</button>);
}function Board({ xIsNext, squares, onPlay }) {function handleClick(i) {if (calculateWinner(squares) || squares[i]) {return;}const nextSquares = squares.slice();if (xIsNext) {nextSquares[i] = 'X';} else {nextSquares[i] = 'O';}onPlay(nextSquares);}const winner = calculateWinner(squares);let status;if (winner) {status = 'Winner: ' + winner;} else {status = 'Next player: ' + (xIsNext ? 'X' : 'O');}return (<><div className="status">{status}</div><div className="board-row"><Square value={squares[0]} onSquareClick={() => handleClick(0)} /><Square value={squares[1]} onSquareClick={() => handleClick(1)} /><Square value={squares[2]} onSquareClick={() => handleClick(2)} /></div><div className="board-row"><Square value={squares[3]} onSquareClick={() => handleClick(3)} /><Square value={squares[4]} onSquareClick={() => handleClick(4)} /><Square value={squares[5]} onSquareClick={() => handleClick(5)} /></div><div className="board-row"><Square value={squares[6]} onSquareClick={() => handleClick(6)} /><Square value={squares[7]} onSquareClick={() => handleClick(7)} /><Square value={squares[8]} onSquareClick={() => handleClick(8)} /></div></>);
}export default function Game() {//const [xIsNext, setXIsNext] = useState(true);//初始化为一个[[null,null.......null]],二维数组const [history, setHistory] = useState([Array(9).fill(null)]);const [currentMove, setCurrentMove ]= useState(0);// const currentSquares = history[history.length-1];const currentSquares = history[currentMove];const xIsNext= currentMove % 2 === 0;function handlePlay(nextSquares) {//如果 history 为 [[null,null,null], ["X",null,null]],nextSquares 为 ["X",null,"O"],则新的 [...history, nextSquares] 数组将为 [[null,null,null], ["X",null,null], ["X",null,"O"]]// setHistory([...history, nextSquares]);// setXIsNext(!xIsNext);const nextHistory = [...history.slice(0, currentMove + 1), nextSquares];setHistory(nextHistory);setCurrentMove(nextHistory.length - 1)}const moves=history.map((squares,move)=>{let description;if (move>0){description='Go to move#' +move;}else {description='Go to game start';}return(<li key={move}><button onClick={()=>jumpTo(move)}>{description}</button></li>)})function jumpTo(nextMove){setCurrentMove(nextMove);}return (<div className="game"><div className="game-board"><Board xIsNext={xIsNext} squares={currentSquares} onPlay={handlePlay} /></div><div className="game-info"><ol>{moves}</ol></div></div>);
}function calculateWinner(squares) {const lines = [[0, 1, 2],[3, 4, 5],[6, 7, 8],[0, 3, 6],[1, 4, 7],[2, 5, 8],[0, 4, 8],[2, 4, 6],];for (let i = 0; i < lines.length; i++) {const [a, b, c] = lines[i];if (squares[a] && squares[a] === squares[b] && squares[a] === squares[c]) {return squares[a];}}return null;
}相关文章:

React实战学习(一)_棋盘设计
需求: 左上侧:状态左下侧:棋盘,保证胜利就结束 和 下过来的不能在下右侧:“时光机”,保证可以回顾,索引 语法: 父子之间属性传递(props)子父组件传递(写法上&…...

【LeetCode】每日一题:三数之和
解题思路 最开始是打算沿着二数之和的思路做,即固定了最大的,然后小的开始遍历,因为这种遍历方式只需要遍历一轮就能完成,所以复杂度应该是O(n2),但是最后几个示例还是超时了,可能进…...

逆风而行:提升逆商,让困难成为你前进的动力
一、引言 生活,总是充满了未知与变数。有时,我们会遇到阳光明媚的日子,享受着宁静与和谐;但更多时候,我们却不得不面对那些突如其来的坏事件,如工作的挫折、人际关系的困扰、健康的挑战等。这些事件如同突…...

新能源汽车CAN总线故障定位与干扰排除的几个方法
CAN总线是目前最受欢迎的现场总线之一,在新能源车中有广泛应用。新能源车的CAN总线故障和隐患将影响驾驶体验甚至行车安全,如何进行CAN总线故障定位及干扰排除呢? 目前,国内机动车保有量已经突破三亿大关。由于大量的燃油车带来严峻的环境问题,因此全面禁售燃油车的日程在…...
【涵子来信】——社交宝典:克服你心中的内向,世界总有缺陷
内向,你是内向的吗?想必每个人不同,面对的情形也是不同的。 暑假是一个很好的机会,我是可以去多社交社交。但是,面对着CSDN上这么多技术人er,那么,我的宝典,对于大家,有…...

LabVIEW项目外协时选择公司与个人兼职的比较
在选择LabVIEW项目外协合作伙伴时,外协公司和个人兼职各有优劣。个人兼职成本较低且灵活,但在可靠性、技术覆盖面、资源和风险管理上存在不足。而外协公司拥有专业团队、丰富资源、完善的项目管理和风险控制,尽管成本较高,但能提…...

汽车电子工程师入门系列——CAN 规范系列通读
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

泽众云真机-平台华为机型HarmonyOS NEXT系统已上线!
泽众云真机平台华为机型HarmonyOS NEXT系统已上线! 之前文章《泽众云真机-平台即将升级支持华为机型HarmonyOS NEXT系统泽众云真机-平台即将升级支持华为机型HarmonyOS NEXT系统》,为什么要升级HarmonyOS NEXT系统?我们之前有说过,…...

AI基础:从线性回归到梯度下降
一个简单的问题: 如果此时你正站在迷路缭绕的山坡上,能见度不高,但是你又想去往最低的山谷的位置,怎么走? 很简单,哪里陡那就往那里走呗——而这就是梯度下降算法的思想。 古话说:“先发制于人…...

AI产品经理面试
把优秀当习惯把优秀当习惯肯定不是口头说说,那有什么判断标准吗? 当我做完一件事儿的时候,我会看它有没有突破我的舒适圈、能不能惊艳到我自己。这就是我的判断标准。 在自我介绍和经历介绍时,面试者应该注重以下几个方面…...

二进制方式部署consul单机版
1.consul的下载 mkdir -p /root/consul/data && cd /root/consul wget https://releases.hashicorp.com/consul/1.18.0/consul_1.18.0_linux_amd64.zip unzip consul_1.18.0_linux_amd64.zip mv consul /usr/local/bin/ 2.配置文件 // 配置文件路径: /roo…...

SpringBoot整合Quartz实现动态定时任务
目录 1、Quartz简介1.1 Quartz的三大核心组件1.2 CronTrigger配置格式 2、SpringBoot整合Quartz框架2.1 创建项目2.2 实现定时任务 1、Quartz简介 Quartz是一个开源的任务调度服务,它可以独立使用,也可与其它的Java EE,Java SE应用整合使用。…...

qt 用宏控制静态接口的统一
1.概要 /** * 单件宏实验 * 创建一个可以生成单件的宏 * 起因:想让有些控件单件,但是c不支持静态的继承(c#支持) * 那么如果保证这些接口的统一呢,用宏 */ 2.代码 2.1 a.h #ifndef A_H #define A_H#include &…...

pdf怎么转换成jpg,本地转换还是在线转换?
PDF(Portable Document Format)和JPG(Joint Photographic Experts Group)这两种文件格式在我们的日常生活和工作中扮演着举足轻重的角色。PDF因其跨平台、保持原样性强的特点,被广泛应用于文件传输和存储;而…...

【物联网】802.15.4简介
目录 一、概述 二、802.15.4主要特点 2.1 工作频段和数据速率 2.2 支持简单器件 2.3 信标方式和超帧结构 2.4 数据传输和低功耗 三、低功耗 一、概述 802.15.4包括用于低速无线个人域网(LR-WPAN)的物理层和媒体接入控制层两个规范。它能支持消耗功率最少,一般…...

C++基础语法:复制构造函数,赋值构造函数及浅复制,深复制
前言 "打牢基础,万事不愁" .C的基础语法的学习 引入 前一篇帖子C基础语法:类构造函数之普通构造函数-CSDN博客讲了普通构造函数,还有 复制构造函数,赋值运算符以及延伸出来的浅复制和深复制问题,做个补充. 内容主要参考自<<C Prime Plus>> 6th Edition …...

架构是怎样练成的-楼宇监控系统案例
目录 概要 项目背景 原系统设计方案 改进后的设计方案 小结 概要 绝大多数人掌握的架构都是直接学习,慢慢地才能体会到一个架构的好处。架构是一种抽象,是为了复用目的而对代码做的抽象。通过一个项目的改造,理解架构是如何产生的&…...
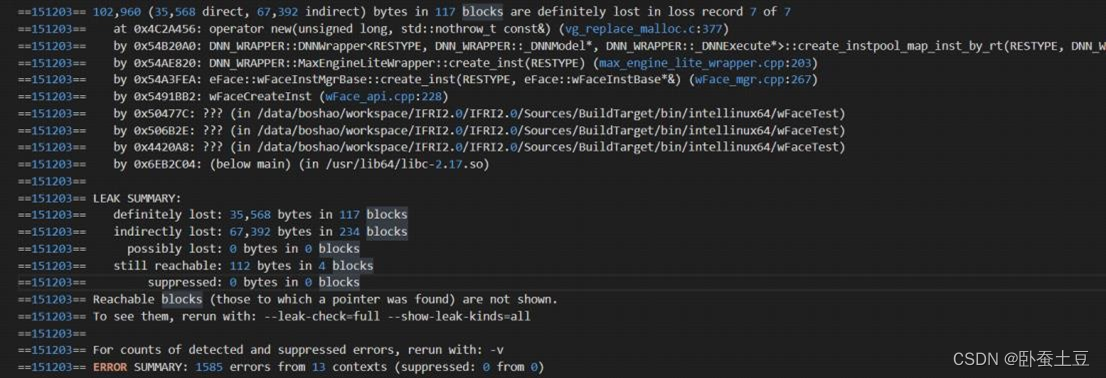
valgrind使用浅谈
1、Valgrind 简介 Valgrind是一款用于内存调试、内存泄漏检测以及性能分析的软件开发工具,它可在以下平台上运行: X86/Linux、AMD64/Linux、ARM/Linux、ARM64/Linux、PPC32/Linux、PPC64/Linux、PPC64LE/Linu x、S390X/Linux、MIPS32/Linux、MIPS64/Li…...
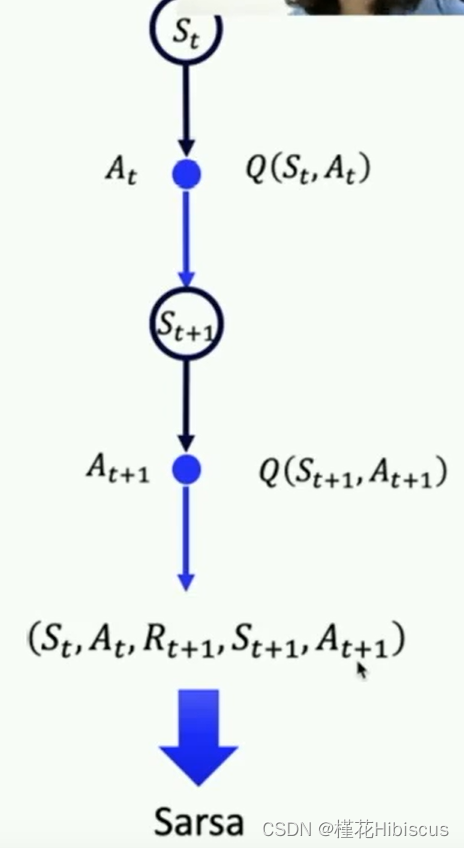
强化学习专题:强化学习知识梳理(一)
2024/6/23: 前段时间有幸完成了大学期间的第一篇论文。在面试之前复盘一下关于自己论文中DQN的一些相关点。 浅谈主要区别(在线 or 离线) 首先,一切的开始是强化学习中时序差分方程,这体现了强化学习方法的优化策略。在…...

深入JVM:详解JIT即时编译器
文章目录 深入JVM:详解JIT即时编译器一、序言二、基础概念1、何为JIT即时编译2、热点代码 三、HotSpot内置的即时编译器1、C1编译器2、C2编译器3、分层编译3.1 协作流程 四、常见JIT优化技术1、方法内联2、逃逸分析(1)同步锁消除(…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
