信息学奥赛初赛天天练-39-CSP-J2021基础题-哈夫曼树、哈夫曼编码、贪心算法、满二叉树、完全二叉树、前中后缀表达式转换

PDF文档公众号回复关键字:20240629

2022 CSP-J 选择题

单项选择题（共15题，每题2分，共计30分：每题有且仅有一个正确选项）

5.对于入栈顺序为a,b,c,d,e的序列，下列( )不合法的出栈序列

A. a，b，c，d，e

B. e，d，c，b，a

C. b，a，c，d，e

D. c，d，a，e，b

8.如果一颗二叉树只有根节点，那么这棵二叉树高度为1。请问高度为5的完全二叉树有( )种不同的形态

A. 16

B. 15

C. 17

D. 32

9.表达式a* (b+c)* d的后缀表达式为( ),其中 *和 +是运算符

A. * * a + b c d

B. a b c + * d *

C. a b c + d * *

D. * a * + b c d

11.在数据压缩编码中的哈夫曼编码方法，在本质上是一种( ) 策略

A. 枚举

B. 贪心

C. 递归

D. 动态规划

15.有四个人要从A点坐一条船过河到B点，船一开始在A点。该船一次最多可坐两个人。已知这四个人中每个人独自坐船的过河时间分别为1、2、4、8，且两个人坐船的过河时间为两人独自过河时间的较大者。则最短( )时间可以让四个人都过河到B点(包括从B点把船开回A点的时间)

A. 14

B. 15

C. 16

D. 17

2 相关知识点

栈

栈又名堆栈，是一种限定仅在表尾进行插入和删除操作的线性表，这一端称为栈顶，另一端称为栈底

栈中的数据元素遵守后进先出的原则

二叉树

每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点)，并且，二叉树的子树有左右之分，其次序不能任意颠倒，例如下面是一棵二叉树

满二叉树

满二叉树又叫完美二叉树，除了叶子结点之外的每一个结点都有两个孩子，树的叶子节点均在最后一层（也就是形成了一个完美的三角形）

完全二叉树

除了最下层，其他每层都饱满，去除最后一层是一棵满二叉树，最下层的结点都集中在该层最左边的若干位置上

前缀表达式

前缀表达式，也称为波兰表达式,是一种算术表达式表示方法，其中运算符位于操作数之前.

//示例1 中缀表达式a+b对应的前缀表达式
+a bC++
//示例2 中缀表达式3+4*2对应的前缀表达式
+ 3 * 4 2 

中缀表达式

是一种常见的算术表达式表示方法，其中运算符位于操作数之间

//示例1
3 + 4 * 2
//示例2
(1 + 2) * (3 - 4)C++

后缀表达式

后缀表达式，也称为逆波兰表达式，是一种算术表达式表示方法，其中运算符位于操作数之后

//示例1 中缀表达式a+b对应的后缀表达式C++
a b+
//示例2 中缀表达式3+4*2对应的前缀表达式3 4 2 * +    

中缀表达式转后缀表达式

确定优先级，按优先级逐一处理操作符(把操作符从操作数中间移到操作数后边)
例如如下中缀表达式转为后缀表达式
1 + ( 2 + 3)* 4 ) – 5
// 按优先级对表达式数字加括号
((1 + (( 2 + 3)* 4 )) – 5 )  
//从最里面的一层括号开始运算，转换成后缀表达式
//转换方法，去除括号，数字在前，顺序不变，操作符移到最后
1. ( 2 + 3) => 2 3 +
//  ( 2 + 3)可以看作一个整体x
2. (( 2 + 3)* 4 ) => (x+4) => x 4 + => 2 3 + 4 *
//(( 2 + 3)* 4 )看作一个整体x
3. (1 + (( 2 + 3)* 4 ))=> (1+x)=>1 x + = 1 2 3 + 4 * +
// (1 + (( 2 + 3)* 4 )) 看作一个整体x
4. ((1 + (( 2 + 3)* 4 )) – 5 ) =>(x-5)=>x 5 - => 1 2 3 + 4 * + 5 -
所以转换后的后缀表达式为 1 2 3 + 4 * + 5 -

哈夫曼树

1 选剩下的两棵根权值最小的树合并成一棵新树

2 新树的根权值等于两棵合并前树的根权值和

3 重复1和2

哈夫曼编码

哈夫曼树的左右孩子进行编码称为哈夫曼编码，通常左边为0，右边为1

只对叶子节点进行编码/解码，编码唯一

哈夫曼编码是前缀编码，任何一个字符的编码都不是另一个字符编码的前缀(只有叶子节点编码)

哈夫曼编码左边为0，右边为1是通常规定，也可以左边为1右边为0，但确定后编码是唯一的

如果下图为字母a,b,c,d,e的编码，字母旁边对应数字为其出现的频率

贪心算法

所谓贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择 。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的 局部最优解

哈夫曼编码总是把出现频率少的编码相对较长，从而保证全局总的编码最短

哈夫曼编码使用的是贪心算法进行编码

3 思路分析

5.对于入栈顺序为a,b,c,d,e的序列，下列( D )不合法的出栈序列

A. a，b，c，d，e

B. e，d，c，b，a

C. b，a，c，d，e

D. c，d，a，e，b

分析

根据入栈出栈性质模拟，栈为后进先出

A a 进 a 出 b 进 b 出 c 进 c 出 d 进 d 出 e 进 e 出 出栈顺序合法
B a 进 b 进 c 进 d 进 e 进 e 出 d 出 c 出 b 出 a 出 出栈顺序合法
C a 进 b 进 b 出 a 出 c 进 c 出 d 进 d 出 e 进 e 出 出栈顺序合法
D a 进 b 进 c 进 c 出 d 进 d 出 此时b在栈顶，a无法出栈 
所以选 D

8.如果一颗二叉树只有根节点，那么这棵二叉树高度为1。请问高度为5的完全二叉树有( A )种不同的形态

A. 16

B. 15

C. 17

D. 32

分析

完全二叉树，除最后一层，其他层都是满的
高度为5有4层是满的，后面1层节点是前面节点的2倍(1个父节点都有2个子节点)
前4层是满的，形态不会变化，只有第5层形态可能变化，第5层节点只要保证从左到右排即可
具体如下
满二叉树
高度为1  1个节点  2^1-1=1
高度为2  1+2 个节点 2^2-1=3
高度为3  1+2+4个节点 2^3-1=7
高度为4  1+2+4+8 个节点2^4-1=15
高度为5  1+2+4+8+16 个节点 2^5-1=31
由于是完全二叉树，说明第5层必有节点,第5层的节点最多可以31-15=16个
当第5层节点为16个时，此时是5层的满二叉树，是特殊的完全二叉树
因此有16种不同的形态

9.表达式a* (b+c)* d的后缀表达式为( B ),其中 *和 +是运算符

A. * * a + b c d

B. a b c + * d *

C. a b c + d * *

D. * a * + b c d

分析

确定优先级，按优先级逐一处理操作符(把操作符从操作数中间移到操作数后边)
a * (b+c)* d  -- ((a * (b+c))* d)((a * (b+c))* d)    
1 (b+c) => b c+ 
//  (b+c)  可以看作一个整体x
(a * (b+c)) => (a * x) => a x * => a b c + *
//(a * (b+c)) 可以看作一个整体x((a * (b+c))* d)  => (x * d) => x d * => a b c + * d * 

11.在数据压缩编码中的哈夫曼编码方法，在本质上是一种( B ) 策略

A. 枚举

B. 贪心

C. 递归

D. 动态规划

分析

哈夫曼编码总是把出现频率少的编码相对较长，从而保证全局总的编码最短

哈夫曼编码使用的是贪心算法进行编码

15.有四个人要从A点坐一条船过河到B点，船一开始在A点。该船一次最多可坐两个人。已知这四个人中每个人独自坐船的过河时间分别为1、2、4、8，且两个人坐船的过河时间为两人独自过河时间的较大者。则最短( B )时间可以让四个人都过河到B点(包括从B点把船开回A点的时间)

A. 14

B. 15

C. 16

D. 17

分析

贪心算法解决此问题，贪心策略

1从剩余的人中选择用时最小的2人过河

2 用时最小的人返回去接剩余的人

1 初始 1 2 4 8 在河的A边

2从剩余的 1 2 4 8 找用时最少的2人(1 和 2)过河到B ,用时为2

3 在B端选择用时间最少的去接，1去接，用时1

4 从剩余的 4 8 找用时最少的2人(4 和 8)过河到B ,用时为8

5 在B端选择用时间最少的去接，2去接，用时2

6 从剩余的 1 2 过河 用时为2

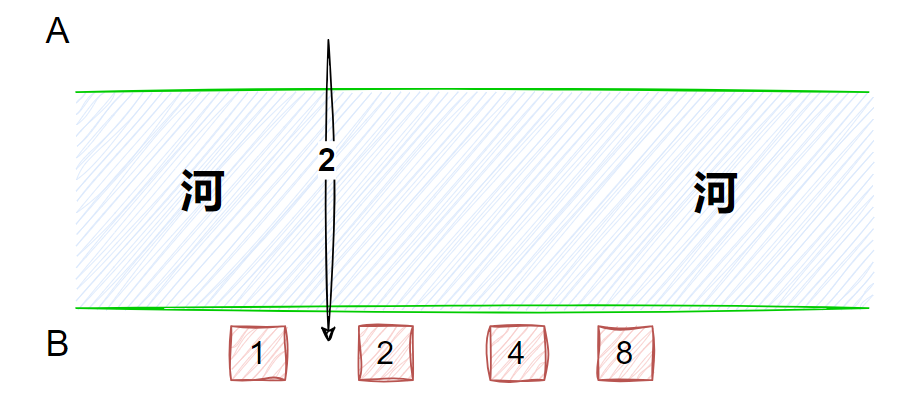
上述过河时间累加 2+1+8+2+2=15