数字信号处理实验一(离散信号及离散系统的MATLAB编程实现)
实验要求:
- 离散信号及离散系统的MATLAB编程实现(2学时)
- 要求:
- 编写一程序,输出一定长度(点数),具有一定幅度、(角)频率和初始相位的实(或复)信号序列,如复指数序列;
- 利用matlab,求系统y(n)-0.8y(n-1)-0.5y(n-2)=0.7x(n)+0.3(n-1)的零极点。
- 目的:
- 熟悉MATLAB命令和编辑、运行、调试环境;
- 学会编写MATLAB程序(.m文件)
- 要求:
实验报告:
一、实验内容
i.设计一个最小阶次的低通FIR数字滤波器,性能指标为:通带0Hz~1500Hz,阻带截止频率2000Hz,通带波动不大于1%,阻带波动不大于1%,采样频率为8000Hz;
ii.用一个仿真信号来验证滤波器的正确性(注意:要满足幅度要求和线性相位特性)。
二、实验目的
i.利用学习到的数字信号处理知识解决实际问题;
ii.了解线性相位滤波器的特殊结构;
三、涉及实验的相关情况介绍(包含使用软件或实验设备等情况)
Windows系统 Matlab 2022b
四、实验记录
1.原理基础
FIR(有限脉冲响应)滤波器是一种数字滤波器,其脉冲响应在有限的时间内衰减为零。FIR滤波器通过一系列加权系数的线性组合对输入信号进行卷积,以产生输出信号。对于低通FIR滤波器,它允许低频信号通过并抑制高频信号。
线性相位FIR滤波器具有对称或反对称的系数,这保证了滤波器在所有频率上具有相同的相位延迟,这对于避免信号失真非常重要。
设计FIR滤波器时,常用的方法有窗函数法、最小二乘法(如firls函数)和等波纹法(如remez函数)。这些方法通过最小化通带和阻带内的误差来优化滤波器的性能。
2 实验流程
①确定滤波器参数:
包括采样频率、通带和阻带截止频率、通带和阻带波动等。
②设计FIR滤波器:
使用MATLAB的firls或remez函数设计满足性能要求的FIR滤波器。
③生成仿真信号:
创建一个包含通带和阻带频率分量的仿真信号。
④应用滤波器:
使用MATLAB的filter函数将设计的FIR滤波器应用于仿真信号。
⑤分析滤波结果:
绘制原始信号和滤波后信号的频谱图,检查通带和阻带的波动是否满足要求,并验证滤波器的线性相位特性。
3 源程序代码
%名称:模拟信号采样与重构及频谱分析FFT
%结构:1.模拟信号的采样 2.生成复合信号并绘制时域和频域 3.应用滤波器并绘制时域频域
%编辑人:贾雯爽
%目的:掌握模拟信号的采样、重构和频谱分析
%最后更新时间:2024/06/05
%模拟信号采样、重构、频谱分析%1.模拟信号的采样(参数设置、创建模拟信号、信号采样、绘制图像)%1.1 设置参数
Fs = 1000;%采样频率
A = 1;%幅度
f0 = 5;%频率
t = 0:1/Fs:1-1/Fs;%时间向量%1.2 信号生成
x = A*sin(2*pi*f0*t);%1.3 信号采样
Ts = 1/Fs;
t_sample = 0:Ts:1-Ts; % 采样时间点
x_sample = A*sin(2*pi*f0*t_sample);% 第四步:绘制原始信号和采样信号
figure;
subplot(3,1,1);
plot(t, x);
title('原始模拟信号');
xlabel('时间 (s)');
ylabel('幅度'); subplot(3,1,2);
stem(t_sample, x_sample, 'filled');
title('采样信号');
xlabel('时间 (s)');
ylabel('幅度'); %2.信号重构(模拟)%2.1 模拟信号重构
t_recon = linspace(0, 1, Fs*10); % 用于重构的更细粒度时间向量
x_recon = interp1(t_sample, x_sample, t_recon, 'linear'); % 线性插值 %2.2 绘制信号重构
subplot(313);
plot(t_recon, x_recon);
title('重构模拟信号');
xlabel('时间(s)');
ylabel('幅度');%3.频谱分析(fft) 原始信号与分析后信号对比%3.1 对原始信号进行FFT频谱分析
N = length(t);
X = fft(x, N);
P2 = abs(X/N);%转换为单边谱
P1 = P2(1:N/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(N/2))/N; % 频率向量 % 3.2绘制原始信号的频谱
figure;
subplot(211);
plot(f, P1);
title('原始模拟信号的频谱');
xlabel('频率 (Hz)');
ylabel('|P(f)|'); % 3.3对采样信号进行FFT
N_sample = length(t_sample);
X_sample = fft(x_sample, N); % 使用与原始信号相同的FFT长度
%取单边频谱的流程
P2_sample = abs(X_sample/N);
P1_sample = P2_sample(1:N/2+1);
P1_sample(2:end-1) = 2*P1_sample(2:end-1); % 3.4绘制采样信号的频谱
subplot(212);
plot(f, P1_sample);
title('采样信号的频谱');
xlabel('频率 (Hz)');
ylabel('|P(f)|'); % 程序结束
4 实验结果

5实验结果分析
i. 对于复指数序列,可以观察到序列的周期性、幅度、频率和相位的变化。这些参数对信号分析和处理非常重要。
ii. 通过对系统差分方程零点和极点的分析,可以了解系统的稳定性和动态特性。在本例中,极点都位于单位圆内,说明系统是稳定的。此外,零点的位置可以影响系统的频率响应特性。通过零极点图,可以直观地看到系统的零点和极点在复平面上的位置,从而进一步分析系统的性能。
五、实验总结
本次实验着重点有两个;①熟悉Matlab的使用操作,包括文件建立、路径添加等。②熟练掌握复指数序列的概念并掌握通过差分方程推到H(z),进一步进行零极点分析的过程。
零极点对数字信号处理系统的性能有着重要作用,稳定性,因果性,低通高通等……
原创文章内容,学术不精恐有错漏之处,恳请各位批评指正。如有Matlab代码源文件或其他沟通需要,可通过邮箱(2642610289@qq.com)联系我,特情注意,学业繁忙难以及时回复,敬请理解。
相关文章:

数字信号处理实验一(离散信号及离散系统的MATLAB编程实现)
实验要求: 离散信号及离散系统的MATLAB编程实现(2学时) 要求: 编写一程序,输出一定长度(点数),具有一定幅度、(角)频率和初始相位的实(或复&…...

数字图像处理专栏——introduction
Introduction: 数字图像处理技术是我在深入学习研究的方向之一。本科期间跟随导师做基于AndroidOpenCV的病虫识别app,因此入门,我也对该部分知识有进一步探索的欲望,但更多的是因该脚踏实地一步步记录,一步步成长。 本篇从数字图…...

Django 模版继承
1,设计母版页 Test/templates/6/base.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><!-- 修正了模板标签的全角字符问题 -->{% block title %}<title>这个是母版页</title>{…...
)
Apipost接口测试工具的原理及应用详解(一)
本系列文章简介: 随着软件行业的快速发展,API(应用程序编程接口)作为不同软件组件之间通信的桥梁,其重要性日益凸显。API的质量直接关系到软件系统的稳定性、性能和用户体验。因此,对API进行严格的测试成为…...
一款轻量级的通信协议---MQTT (内含Linux环境搭建)
目录 MQTT MQTT的关键特点: 应用场景 Linux环境搭建: 1. 安装mosquitto 2. Linux下客户端进行通信 3. PC端和Linux下进行通信 安装MQTT. fx 4. MQTT.fx的使用 1. 点击连接 编辑 2. 连接成功 3. 订阅主题或者给别的主题发送消息 遇到的问…...

记netty本地客户端断线无法自动重连 or 远程客户端自动重连本地服务端
记netty客户端断线无法自动完成重连 or 服务端无法让客户端断线重连 引场景案例bootstrap 引 netty既能开发socket服务端,也可开发客户端,实现连接的全双工通信。在客户端断线重启后,可自动重连服务端。 场景 本地代码既有socket客户端也有…...

UNIAPP_在js文件中使用i18n国际化
导入 import { initVueI18n } from dcloudio/uni-i18n import messages from /locale/index const { t } initVueI18n(messages) 使用 t(config.request.i001)....
第三节:如何理解Spring的两个特性IOC和AOP(自学Spring boot 3.x第一天)
大家好,我是网创有方,接下来教大家如何理解Spring的两个特性IOC和AOP。本节有点难,大家多理解。 IOC(控制反转) 定义与核心思想: IOC,全称Inversion of Control,即控制反转。 其核…...
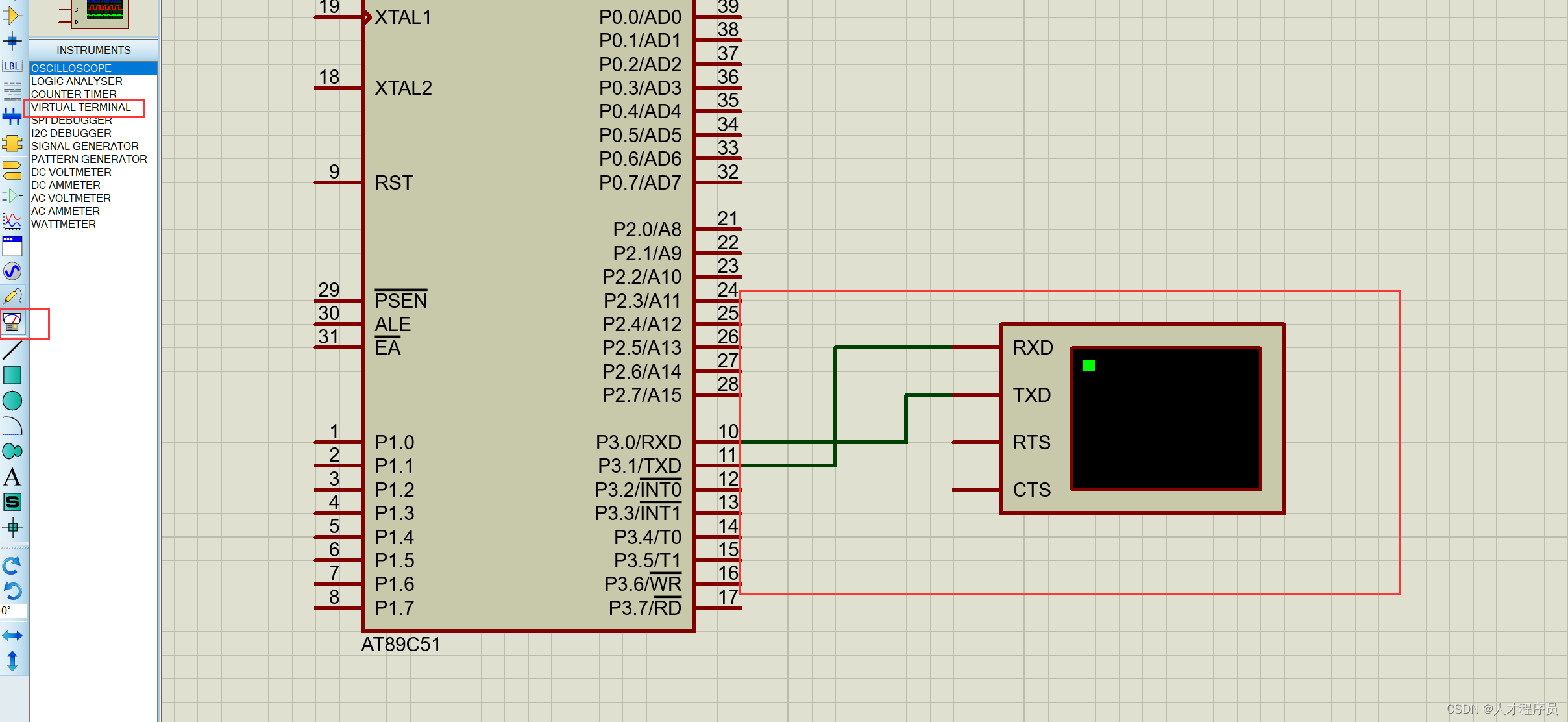
【51单片机】串口通信(发送与接收)
文章目录 前言串口通信简介串口通信的原理串口通信的作用串口编程的一些概念仿真图如何使用串口初始化串口串口模式波特率配置 发送与接收发送接收 示例代码 总结 前言 在嵌入式系统的开发中,串口通信是一种常见且重要的通信方式。它以其简单、稳定的特性在各种应用…...
)
【AI研发工具包】sklearn教程(Scikit-learn)
目录 1. 引言 2. 安装sklearn 3. 导入sklearn 4. 加载数据集 5. 数据预处理 6. 训练模型 7. 评估模型 8. 保存和加载模型 9. 自定义数据 10. 深入sklearn 11. 注意事项 1. 引言 Scikit-learn(简称sklearn)是Python中一个非常流行的机器学习库…...

数位DP——AcWing 1081. 度的数量
数位DP 定义 数位DP是一种动态规划技巧,特别适用于处理与数字的位操作相关的问题,如数字序列的计数、数字的生成等问题。它通过将问题分解为对每一位数字的独立考虑,从而简化问题复杂度,实现高效求解。 数位DP的核心思想是将原…...

2024下半年必追国漫片单,谁将问鼎巅峰?
随着2024年上半年的落幕,国漫市场再度迎来了百花齐放的盛况。从经典续作到全新IP,从玄幻到科幻,每一部作品都以其独特的魅力吸引着观众的目光。本期为大家盘点下半年值得一看的国漫佳作,大胆预测,谁将成为这场神仙打架…...
信息发布小程序h5 uniapp thinkphp
纯手工uniapp thinkphp 全开源打造 信息发布小程序 一、概述 信息发布小程序是一种基于微信平台的小程序应用,旨在为用户提供便捷的信息发布与展示服务。用户可以通过该小程序快速发布各类信息,如招聘、寻物、公告等,同时也可以浏览和搜索…...
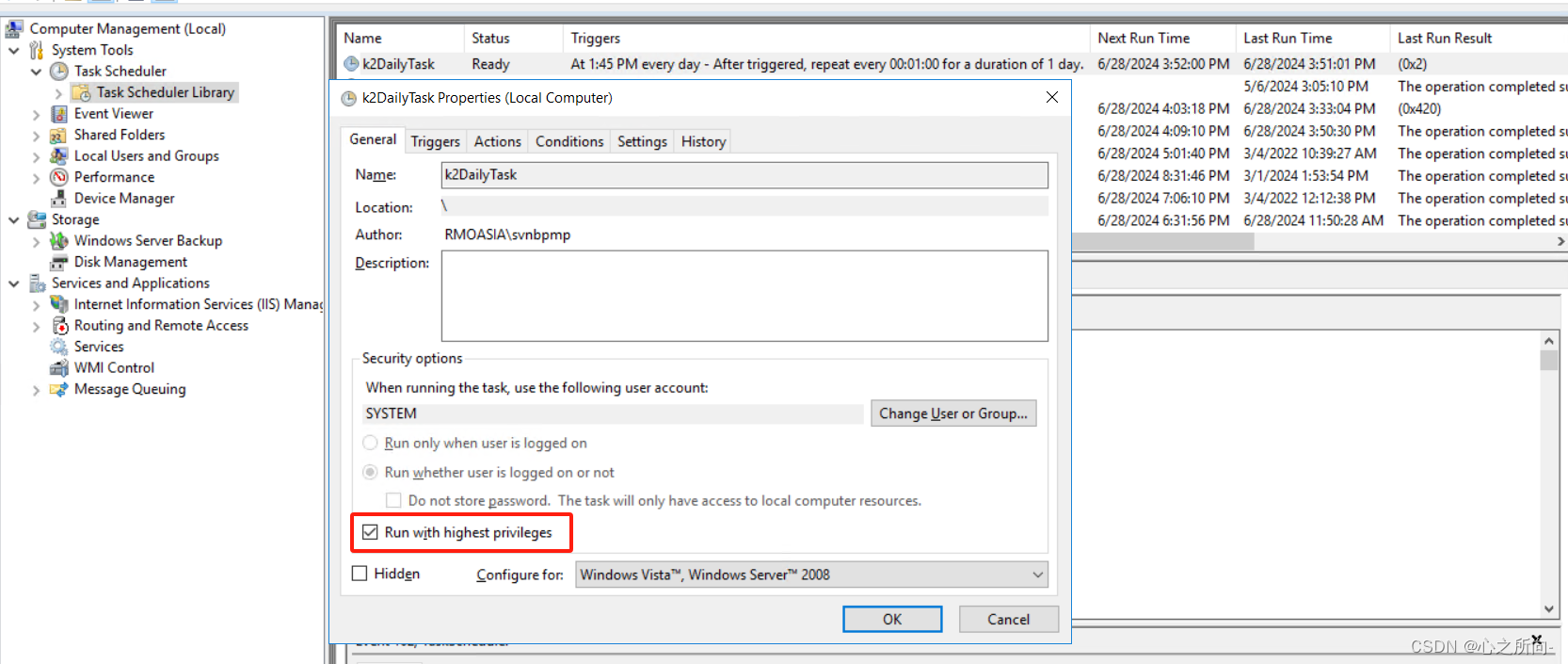
Windows定时任务执行脚本
场景:由于网络波动原因导致云数据库没连接上,从而导致某个流程引擎链接不上数据库从而导致该流程引擎服务挂了,网络恢复后 数据库链接正常,但是该引擎服务还是中止状态。 解决方案:在Windows中新建一个定时任务&#…...

优维“统一开放平台”:开放、开发、集成、客制化
基于丰富完善的产品体系,优维重磅推出了统一开放平台。这款由优维自主设计与研发,集数据开发、能力开放、能力集成、客制化为一体的统一开放平台,具备应用市场、应用开发、连接能力、采控平台、API集市、开发者工具等功能模块,可为…...

ChatGPT新纪元:揭秘GPT-4o的多模态能力
GPT-4o登场 探索ChatGPT的多模态创新 今日凌晨,OpenAI向全球宣布了AI发展的新篇章——GPT-4o,每次OpenAI发布重大更新时,尽管令人兴奋,但也不免使众多初创公司的梦想破灭。 GPT-4o的命名中的“o”象征着“omni”——全能的代表。…...

泰勒斯威夫特2022年纽约大学毕业典礼演讲:NYU‘s 2022 Commencement Speaker Taylor Swift
NYU’s 2022 Commencement Speaker Taylor Swift Link: https://www.youtube.com/watch?vOBG50aoUwlI Singer, songwriter, producer, and director Taylor Swift received a Doctor of Fine Arts, honoris causa, at the Commencement for the Class of 2022 and delivered …...
SvelteKit教程:调用外部 API 获取数据)
(四)SvelteKit教程:调用外部 API 获取数据
(四)SvelteKit教程:调用 API 我们先按照如下的方式来构建api服务: step 1:npm i json-serverstep 2:在根目录下新建 db.json 文件,内部写入如下内容:{"users": [{"id": 1,"name…...

数据结构-分析期末选择题考点(排序)
何似清歌倚桃李 一炉沈水醉红灯 契子 ✨ 上一期给大家提供了大概会考的题型给老铁们复习的大致思路 这一期还会是一样,我将整理一下排序的题型以及解题方法给你们 由于时间还很多,我就慢慢总结吧,一天一章的样子,明天总结串、后天…...

Python:探索高效、智能的指纹识别技术(简单易懂)
目录 概括 导入库 函数一 参数: 函数二 函数三 主函数 运行结果 src: model_base 7.bmp 编辑 总结 概括 指纹识别是一种基于人体生物特征的身份验证技术。它通过捕捉和分析手指上的独特纹路和细节特征,实现高准确度的身份识别。…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
