【多维动态规划】Leetcode 97. 交错字符串【中等】
交错字符串
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空
子字符串
子字符串 是字符串中连续的 非空 字符序列。
- s = s1 + s2 + … + sn
- t = t1 + t2 + … + tm
- |n - m| <= 1
- 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …
注意:a + b 意味着字符串 a 和 b 连接。
示例 1:
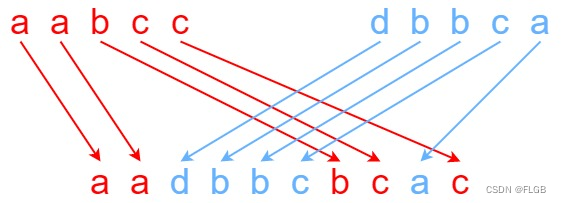
输入:s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出:true
解题思路
定义一个二维布尔数组 dp,其中 dp[i][j] 表示 s3 的前 i + j 个字符是否可以由s1 的前 i 个字符和 s2 的前 j 个字符交错组成。具体的递推关系如下:
初始条件:
- dp[0][0] = true,表示两个空字符串可以组成空字符串。
递推关系:
-
如果 dp[i-1][j] 为真且 s1[i-1] == s3[i + j - 1],则 dp[i][j] = true。
dp[i-1][j] 表示 s3 的前 i + j - 1 个字符可以通过 s1 的前 i-1 个字符和 s2 的前 j 个字符交错组成。
如果 s1 的第 i 个字符 s1[i-1] 等于 s3 的第 i + j 个字符 s3[i + j - 1],
则可以在 s3 的前 i + j - 1 个字符的基础上加上 s1 的第 i 个字符组成 s3 的前 i + j 个字符。
因此,dp[i][j] = true。 -
同理,如果 dp[i][j-1] 为真且 s2[j-1] == s3[i + j - 1],则 dp[i][j] = true。
最终结果:
- dp[s1.length()][s2.length()] 表示 s3 是否可以由 s1 和 s2 交错组成。
Java实现
public class InterleavingString {public boolean isInterleave(String s1, String s2, String s3) {int m = s1.length();int n = s2.length();if (m + n != s3.length()) {return false;}boolean[][] dp = new boolean[m + 1][n + 1];dp[0][0] = true;// 初始化第一列for (int i = 1; i <= m; i++) {dp[i][0] = dp[i-1][0] && s1.charAt(i-1) == s3.charAt(i-1);}// 初始化第一行for (int j = 1; j <= n; j++) {dp[0][j] = dp[0][j-1] && s2.charAt(j-1) == s3.charAt(j-1);}// 填充 dp 表for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = (dp[i-1][j] && s1.charAt(i-1) == s3.charAt(i + j - 1)) || (dp[i][j-1] && s2.charAt(j-1) == s3.charAt(i + j - 1));}}return dp[m][n];}// 测试用例public static void main(String[] args) {InterleavingString solution = new InterleavingString();System.out.println(solution.isInterleave("aabcc", "dbbca", "aadbbcbcac")); // 期望输出: trueSystem.out.println(solution.isInterleave("aabcc", "dbbca", "aadbbbaccc")); // 期望输出: false}
}时间空间复杂度
- 时间复杂度:O(m * n),其中 m 是 s1 的长度,n 是 s2 的长度,需要遍历整个 dp 数组。
- 空间复杂度:O(m * n),需要一个二维数组 dp 存储中间结果。
相关文章:

【多维动态规划】Leetcode 97. 交错字符串【中等】
交错字符串 给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。 两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串 子字符串 是字符串中连续的 非空 字符序列。 s s1 s2 … snt…...

【JavaScript脚本宇宙】精通前端开发:六大热门CSS框架详解
前端开发的利器:深入了解六大CSS框架 前言 在现代Web开发中,选择适合的前端框架和工具包是构建高效、响应式和美观的网站或应用程序的关键。本文将详细介绍六个广受欢迎的CSS框架:Bootstrap、Bulma、Tailwind CSS、Foundation、Materialize…...

开发技术-Java集合(List)删除元素的几种方式
文章目录 1. 错误的删除2. 正确的方法2.1 倒叙删除2.2 迭代器删除2.3 removeAll() 删除2.4 removeIf() 最简单的删除 3. 总结 1. 错误的删除 在写代码时,想将其中的一个元素删除,就遍历了 list ,使用了 remove(),发现效果并不是想…...

c++ 递归
递归函数是指在函数定义中调用自身的函数。C语言也支持递归函数。 下面是一个使用递归函数计算阶乘的例子: #include <iostream> using namespace std;int factorial(int n) {// 基本情况,当 n 等于 0 或 1 时,阶乘为 1if (n 0 || n…...
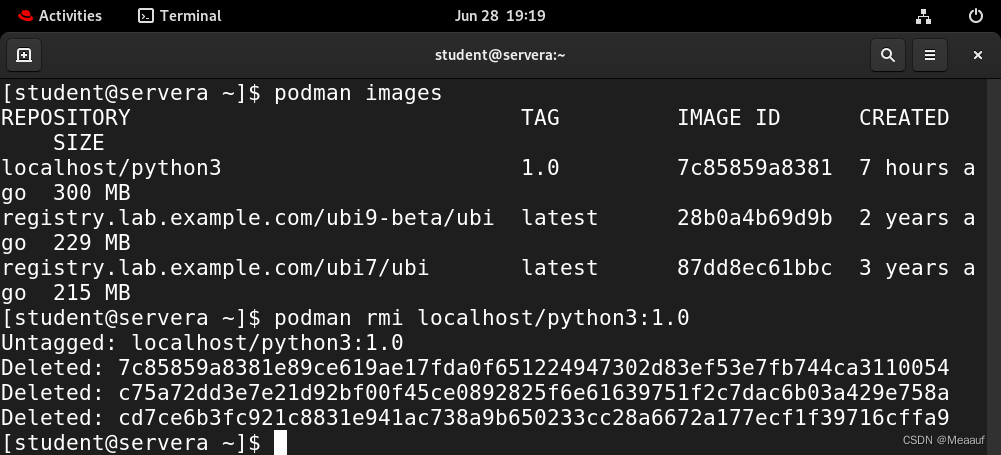
RedHat9 | podman容器
1、容器技术介绍 传统问题 应用程序和依赖需要一起安装在物理主机或虚拟机上的操作系统应用程序版本比当前操作系统安装的版本更低或更新两个应用程序可能需要某一软件的不同版本,彼此版本之间不兼容 解决方式 将应用程序打包并部署为容器容器是与系统的其他部分…...

边缘计算项目有哪些
边缘计算项目在多个领域得到了广泛的应用,以下是一些典型的边缘计算项目案例: 1. **智能交通系统**:通过在交通信号灯、监控摄像头等设备上部署边缘计算,可以实时分析交通流量,优化交通信号控制,减少拥堵&…...

计算fibonacci数列每一项时所需的递归调用次数
斐波那契数列是一个经典的数列,其中每一项是前两项的和,定义为: [ F(n) F(n-1) F(n-2) ] 其中,( F(0) 0 ) 和 ( F(1) 1 )。 对于计算斐波那契数列的第 ( n ) 项,如果使用简单的递归方法,其时间复杂度是…...

【教学类65-05】20240627秘密花园涂色书(中四班练习)
【教学类65-03】20240622秘密花园涂色书03(通义万相)(A4横版1张,一大 68张纸136份)-CSDN博客 背景需求: 打印以下几款秘密花园样式(每款10份)给中四班孩子玩一下,看看效果 【教学类…...
)
Python 学习之基础语法(一)
Python的语法基础主要包括以下几个方面,下面将逐一进行分点表示和归纳: 一、基本语法 1. 注释 a. 单行注释:使用#开头,例如# 这是一个单行注释。 b. 多行注释:使用三引号(可以是三个单引号或三个双引号&…...
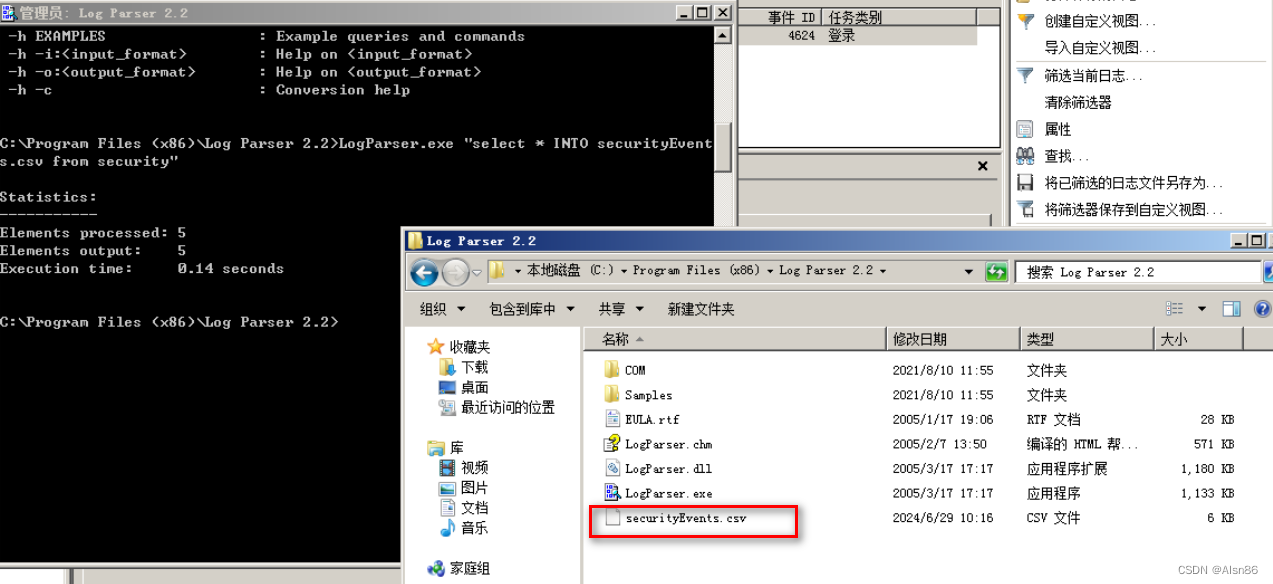
日志分析-windows系统日志分析
日志分析-windows系统日志分析 使用事件查看器分析Windows系统日志 cmd命令 eventvwr 筛选 清除日志、注销并重新登陆,查看日志情况 Windows7和Windowserver2008R2的主机日志保存在C:\Windows\System32\winevt\Logs文件夹下,Security.evtx即为W…...

【ARM】MDK工程切换高版本的编译器后出现error A1137E报错
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 解决工程从Compiler 5切换到Compiler 6进行编译时出现一些非语法问题上的报错。 2、 问题场景 对于一些使用Compiler 5进行编译的工程,要切换到Compiler 6进行编译的时候,原本无任何报错警告…...

深入 SSH:解锁本地转发、远程转发和动态转发的潜力
文章目录 前言一、解锁内部服务:SSH 本地转发1.1 什么是 SSH 本地转发1.2 本地转发应用场景 二、打开外部访问大门:SSH 远程转发2.1 什么是 SSH 远程转发2.2 远程转发应用场景 三、动态转发:SSH 让你拥有自己的 VPN3.1 什么是 SSH 动态转发3.…...

python如何把一个函数的返回值,当成这个函数的参数值
python如何把一个函数的返回值,当成这个函数的参数值 1. 递归调用 递归是一种函数自己调用自己的方法。在递归调用中,你可以将前一次调用的返回值作为下一次调用的参数。 def recursive_function(x):# 函数逻辑if 条件满足:return 结果else:return rec…...

【融合ChatGPT等AI模型】Python-GEE遥感云大数据分析、管理与可视化及多领域案例应用
随着航空、航天、近地空间遥感平台的持续发展,遥感技术近年来取得显著进步。遥感数据的空间、时间、光谱分辨率及数据量均大幅提升,呈现出大数据特征。这为相关研究带来了新机遇,但同时也带来巨大挑战。传统的工作站和服务器已无法满足大区域…...
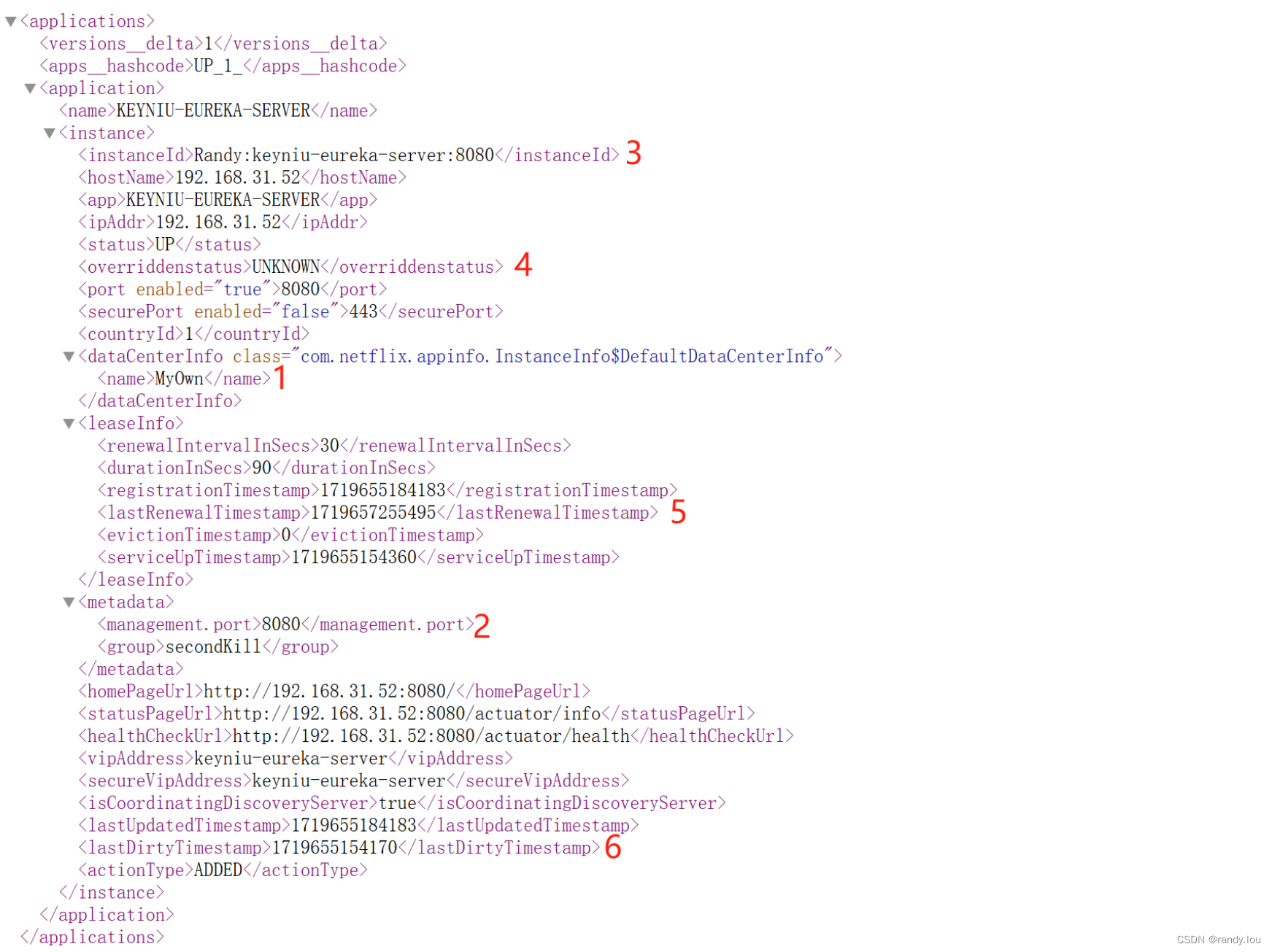
SpringBoot: Eureka入门
1. IP列表 公司发展到一定的规模之后,应用拆分是无可避免的。假设我们有2个服务(服务A、服务B),如果服务A要调用服务B,我们能怎么做呢?最简单的方法是让服务A配置服务B的所有节点的IP,在服务A内部做负载均衡调用服务B…...

Typescript 【实用教程】(2024最新版)含类型声明,类型断言,函数,接口,泛型等
简介 TypeScript 是 JavaScript 的超集,是 JavaScript(弱类型语言) 的强类型版本。 拥有类型机制文件后缀 .tsTypescript type ES6TypeScript 和 JavaScript 的关系类似 less 和 css 的关系TypeScript对 JavaScript 添加了一些扩展&#x…...
智慧校园-实训管理系统总体概述
智慧校园实训管理系统,专为满足高等教育与职业教育的特定需求而设计,它代表了实训课程管理领域的一次数字化飞跃。此系统旨在通过革新实训的组织结构、执行流程及评估标准,来增强学生的实践操作技能和教师的授课效率,为社会输送具…...

如何用GPT开发一个基于 GPT 的应用?
原文发自博客:GPT应用开发小记 如何开发一个基于 GPT 的应用?答案就在问题里,那就是用 GPT 来开发基于 GPT 的应用。本文以笔者的一个开源项目 myGPTReader 为例,分享我是如何基于 GPT 去开发这个系统的,这个系统的功能…...
)
大数据生态体系中各组件的区别面试题(更新)
一、MapReduce与Spark有什么区别? 1、处理方式: MapReduce基于磁盘处理数据,将中间结果保存到磁盘中,减少了内存占用,计算速度慢。 基于内存处理数据,将计算的中间结果保存到内存中,计算速度快。2、资源申请方式&…...

数字信号处理实验一(离散信号及离散系统的MATLAB编程实现)
实验要求: 离散信号及离散系统的MATLAB编程实现(2学时) 要求: 编写一程序,输出一定长度(点数),具有一定幅度、(角)频率和初始相位的实(或复&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
