计算神经网络中梯度的核心机制 - 反向传播(backpropagation)算法(1)
计算神经网络中梯度的核心机制 - 反向传播(backpropagation)算法(1)
flyfish
链式法则在深度学习中的主要应用是在反向传播(backpropagation)算法中。
从简单的开始 ,文本说的就是链式法则
R \mathbb{R} R
- 英文:The set of real numbers
- 解释:符号 R \mathbb{R} R 表示所有实数的集合,包括所有正数、负数和零。在英语中,这个符号称为 “the set of real numbers” 或简称 “the reals”。
- 读作:实数集
- 含义:符号 R \mathbb{R} R 表示所有实数的集合。在数学中,这个符号用来指代从负无穷到正无穷的所有实数。
f ∘ g f \circ g f∘g
- 读作: f f f 复合 g g g
- 含义:符号 ∘ \circ ∘ 表示函数的复合。复合函数 f ∘ g f \circ g f∘g 表示先应用函数 g g g,然后将 g g g 的输出作为函数 f f f 的输入。形式上,这可以写作:
( f ∘ g ) ( x ) = f ( g ( x ) ) (f \circ g)(x) = f(g(x)) (f∘g)(x)=f(g(x))
例子
假设我们有两个函数 g ( x ) = 2 x + 3 g(x) = 2x + 3 g(x)=2x+3 和 f ( u ) = u 3 f(u) = u^3 f(u)=u3,复合函数 f ∘ g f \circ g f∘g 表示为:
( f ∘ g ) ( x ) = f ( g ( x ) ) = f ( 2 x + 3 ) = ( 2 x + 3 ) 3 (f \circ g)(x) = f(g(x)) = f(2x + 3) = (2x + 3)^3 (f∘g)(x)=f(g(x))=f(2x+3)=(2x+3)3
箭头符号的意义
- f : A → B f: A \to B f:A→B 表示函数 f f f 将集合 A A A 中的每个元素映射到集合 B B B 中的一个元素。
- x ↦ f ( x ) x \mapsto f(x) x↦f(x) 表示 x x x 经过函数 f f f 的映射得到 f ( x ) f(x) f(x)。
例子
- 简单映射:
设 f : R → R f: \mathbb{R} \to \mathbb{R} f:R→R 表示一个从实数集合到实数集合的函数。具体的映射可以是:
f ( x ) = x 2 f(x) = x^2 f(x)=x2
这里, f f f 将每个实数 x x x 映射到它的平方 x 2 x^2 x2。 - 复合函数的映射:
如果有两个函数 g g g 和 f f f:
- g : R → R g: \mathbb{R} \to \mathbb{R} g:R→R
- f : R → R f: \mathbb{R} \to \mathbb{R} f:R→R并且 g ( x ) = 2 x + 3 g(x) = 2x + 3 g(x)=2x+3, f ( u ) = u 3 f(u) = u^3 f(u)=u3,那么复合函数 f ∘ g f \circ g f∘g 可以表示为:
( f ∘ g ) ( x ) = f ( g ( x ) ) (f \circ g)(x) = f(g(x)) (f∘g)(x)=f(g(x))
具体的映射是:
g : x ↦ 2 x + 3 g: x \mapsto 2x + 3 g:x↦2x+3
f : u ↦ u 3 f: u \mapsto u^3 f:u↦u3
结合起来:
( f ∘ g ) : x ↦ ( 2 x + 3 ) 3 (f \circ g): x \mapsto (2x + 3)^3 (f∘g):x↦(2x+3)3
函数的映射关系
在数学中,函数的定义和使用广泛应用于各种映射关系中。箭头符号帮助我们清晰地描述这些关系。更具体地:
- 箭头 → \to → 用于描述集合之间的映射关系。
- 箭头 ↦ \mapsto ↦ 用于描述具体的元素如何被映射。
复合函数的表示
复合函数的映射关系可以通过箭头符号更直观地表示:
- g : A → B g: A \to B g:A→B
- f : B → C f: B \to C f:B→C
- 复合函数 f ∘ g f \circ g f∘g 的映射关系为 f ∘ g : A → C f \circ g: A \to C f∘g:A→C
假设 g g g 将 x x x 映射到 u u u,即 g : x ↦ u g: x \mapsto u g:x↦u,并且 f f f 将 u u u 映射到 y y y,即 f : u ↦ y f: u \mapsto y f:u↦y。那么复合函数 f ∘ g f \circ g f∘g 将 x x x 直接映射到 y y y,即:
( f ∘ g ) : x ↦ f ( g ( x ) ) (f \circ g): x \mapsto f(g(x)) (f∘g):x↦f(g(x))
复合函数的概念
如果我们有两个函数:
- g : A → B g: A \to B g:A→B
- f : B → C f: B \to C f:B→C
其中,函数 g g g 将集合 A A A 中的元素映射到集合 B B B,而函数 f f f 将集合 B B B 中的元素映射到集合 C C C。那么,复合函数 f ∘ g f \circ g f∘g 将集合 A A A 中的元素直接映射到集合 C C C,即:
( f ∘ g ) ( x ) = f ( g ( x ) ) (f \circ g)(x) = f(g(x)) (f∘g)(x)=f(g(x))
例子
- 简单的复合函数:
设 g ( x ) = x 2 g(x) = x^2 g(x)=x2 和 f ( u ) = sin ( u ) f(u) = \sin(u) f(u)=sin(u)。复合函数 ( f ∘ g ) ( x ) (f \circ g)(x) (f∘g)(x) 表示为:
( f ∘ g ) ( x ) = f ( g ( x ) ) = sin ( x 2 ) (f \circ g)(x) = f(g(x)) = \sin(x^2) (f∘g)(x)=f(g(x))=sin(x2)
在这个例子中,先计算内部函数 g ( x ) = x 2 g(x) = x^2 g(x)=x2,然后将结果代入到外部函数 f ( u ) = sin ( u ) f(u) = \sin(u) f(u)=sin(u)。 - 其他例子:
设 g ( x ) = 2 x + 3 g(x) = 2x + 3 g(x)=2x+3 和 f ( u ) = u 3 f(u) = u^3 f(u)=u3。复合函数 ( f ∘ g ) ( x ) (f \circ g)(x) (f∘g)(x) 表示为:
( f ∘ g ) ( x ) = f ( g ( x ) ) = ( 2 x + 3 ) 3 (f \circ g)(x) = f(g(x)) = (2x + 3)^3 (f∘g)(x)=f(g(x))=(2x+3)3
假设我们有两个函数 g ( x ) g(x) g(x) 和 f ( u ) f(u) f(u):
- 先绘制 g ( x ) g(x) g(x) 的图形。例如, g ( x ) = x 2 g(x) = x^2 g(x)=x2 是一个抛物线。
- 然后将 g ( x ) g(x) g(x) 的输出代入 f ( u ) f(u) f(u),绘制 f ( g ( x ) ) f(g(x)) f(g(x)) 的图形。例如, f ( u ) = sin ( u ) f(u) = \sin(u) f(u)=sin(u),将 u = x 2 u = x^2 u=x2 代入,得到 sin ( x 2 ) \sin(x^2) sin(x2) 的图形。

import numpy as np
import matplotlib.pyplot as plt# 定义两个函数
def g(x):return x**2def f(u):return np.sin(u)# 生成x的值
x = np.linspace(-2, 2, 400)
y_g = g(x)
y_f = f(y_g)# 初始化图形
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 12))# 绘制函数 g(x)
ax1.plot(x, y_g, label=r'$g(x) = x^2$', color='blue')
ax1.set_title('Function $g(x)$')
ax1.set_xlabel('$x$')
ax1.set_ylabel('$g(x)$')
ax1.legend()# 绘制函数 f(u)
u = np.linspace(0, 4, 400)
ax2.plot(u, f(u), label=r'$f(u) = \sin(u)$', color='green')
ax2.set_title('Function $f(u)$')
ax2.set_xlabel('$u$')
ax2.set_ylabel('$f(u)$')
ax2.legend()# 绘制复合函数 h(x) = f(g(x))
ax3.plot(x, y_f, label=r'$h(x) = \sin(x^2)$', color='red')
ax3.set_title('Composite Function $h(x) = f(g(x))$')
ax3.set_xlabel('$x$')
ax3.set_ylabel('$h(x)$')
ax3.legend()# 调整子图之间的间距
plt.subplots_adjust(hspace=0.5)# 显示图形
plt.show()
链式法则(Chain Rule)是微积分中一个重要的求导法则,它用于求复合函数的导数。复合函数是指一个函数的输入是另一个函数的输出,形式上可以写作 y = f ( g ( x ) ) y = f(g(x)) y=f(g(x))。链式法则告诉我们如何求这种复合函数的导数。
如果我们有两个函数 f f f 和 g g g,其中 y = f ( u ) y = f(u) y=f(u) 且 u = g ( x ) u = g(x) u=g(x),那么根据链式法则,复合函数 y = f ( g ( x ) ) y = f(g(x)) y=f(g(x)) 对 x x x 的导数可以表示为:
d y d x = d y d u ⋅ d u d x \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} dxdy=dudy⋅dxdu
用更直观的方式理解,链式法则表明:
- 首先求出内部函数 u = g ( x ) u = g(x) u=g(x) 对 x x x 的导数,即 d u d x \frac{du}{dx} dxdu。
- 然后求出外部函数 y = f ( u ) y = f(u) y=f(u) 对 u u u 的导数,即 d y d u \frac{dy}{du} dudy。
- 最后将这两个导数相乘,得到复合函数 y = f ( g ( x ) ) y = f(g(x)) y=f(g(x)) 对 x x x 的导数。
例子
假设有函数 y = sin ( x 2 ) y = \sin(x^2) y=sin(x2),我们希望求 y y y 对 x x x 的导数。
- 首先,我们将 y = sin ( x 2 ) y = \sin(x^2) y=sin(x2) 看作两个函数的复合,即 y = sin ( u ) y = \sin(u) y=sin(u) 和 u = x 2 u = x^2 u=x2。
- 对内部函数 u = x 2 u = x^2 u=x2 求导: d u d x = 2 x \frac{du}{dx} = 2x dxdu=2x
- 对外部函数 y = sin ( u ) y = \sin(u) y=sin(u) 求导: d y d u = cos ( u ) \frac{dy}{du} = \cos(u) dudy=cos(u)
- 将这两个结果相乘: d y d x = d y d u ⋅ d u d x = cos ( x 2 ) ⋅ 2 x \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} = \cos(x^2) \cdot 2x dxdy=dudy⋅dxdu=cos(x2)⋅2x
所以, y = sin ( x 2 ) y = \sin(x^2) y=sin(x2) 对 x x x 的导数为:
d y d x = 2 x cos ( x 2 ) \frac{dy}{dx} = 2x \cos(x^2) dxdy=2xcos(x2)
微分符号 d d d 的含义
- 导数的定义:
导数表示函数在某一点的变化率。对于函数 y = f ( x ) y = f(x) y=f(x),它在 x x x 处的导数定义为: d y d x = lim Δ x → 0 Δ y Δ x \frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} dxdy=limΔx→0ΔxΔy这里, Δ y \Delta y Δy 和 Δ x \Delta x Δx 分别表示 y y y 和 x x x 的增量。当这些增量趋近于零时,我们用 d y dy dy 和 d x dx dx 来表示这些非常小的变化量。 - 微分表示法:
微分符号 d d d 用于表示一个函数的微小变化。例如, d x dx dx 表示变量 x x x 的一个非常小的变化量。同样地, d y dy dy 表示函数 y y y 的一个非常小的变化量。如果 y = f ( x ) y = f(x) y=f(x),那么 d y dy dy 表示 y y y 对 x x x 的微小变化,可以表示为: d y = f ′ ( x ) ⋅ d x dy = f'(x) \cdot dx dy=f′(x)⋅dx这里, f ′ ( x ) f'(x) f′(x) 是函数 f ( x ) f(x) f(x) 的导数,表示 x x x 处的变化率。
链式法则中的 d d d
在链式法则中, d d d 表示不同变量的微小变化。例如:
-
d u du du 表示变量 u u u 的微小变化量。
-
d x dx dx 表示变量 x x x 的微小变化量。
-
d y dy dy 表示函数 y y y 的微小变化量。
链式法则告诉我们,当我们有复合函数 y = f ( g ( x ) ) y = f(g(x)) y=f(g(x)) 时, y y y 对 x x x 的变化可以分解为 y y y 对 u u u 的变化以及 u u u 对 x x x 的变化:
d y d x = d y d u ⋅ d u d x \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} dxdy=dudy⋅dxdu
这里,每个 d d d 都表示相应变量的微小变化。例如: -
d y d x \frac{dy}{dx} dxdy 表示 y y y 对 x x x 的变化率。
-
d y d u \frac{dy}{du} dudy 表示 y y y 对 u u u 的变化率。
-
d u d x \frac{du}{dx} dxdu 表示 u u u 对 x x x 的变化率。
通过这样分解,我们可以更容易地计算复合函数的导数。
基于极限和增量来理解链式法则
- 定义复合函数和导数:
- 设 y = f ( u ) y = f(u) y=f(u),其中 u = g ( x ) u = g(x) u=g(x)。
- 我们需要求 y = f ( g ( x ) ) y = f(g(x)) y=f(g(x)) 对 x x x 的导数。
- 增量表示:
- 令 Δ x \Delta x Δx 是 x x x 的一个非常小的增量。
- 相应的, u u u 有一个非常小的增量 Δ u \Delta u Δu,其中 Δ u = g ( x + Δ x ) − g ( x ) \Delta u = g(x + \Delta x) - g(x) Δu=g(x+Δx)−g(x)。
- y y y 的增量表示为 Δ y = f ( g ( x + Δ x ) ) − f ( g ( x ) ) \Delta y = f(g(x + \Delta x)) - f(g(x)) Δy=f(g(x+Δx))−f(g(x))。
- 导数的定义: d y d x = lim Δ x → 0 Δ y Δ x \frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} dxdy=limΔx→0ΔxΔy
- 应用链式法则的思想: Δ y = f ( g ( x + Δ x ) ) − f ( g ( x ) ) \Delta y = f(g(x + \Delta x)) - f(g(x)) Δy=f(g(x+Δx))−f(g(x))可以表示为: Δ y Δ x = f ( g ( x + Δ x ) ) − f ( g ( x ) ) Δ x \frac{\Delta y}{\Delta x} = \frac{f(g(x + \Delta x)) - f(g(x))}{\Delta x} ΔxΔy=Δxf(g(x+Δx))−f(g(x))
- 拆分增量:
由于 u = g ( x ) u = g(x) u=g(x),我们可以引入 Δ u \Delta u Δu: Δ y Δ x = f ( g ( x + Δ x ) ) − f ( g ( x ) ) g ( x + Δ x ) − g ( x ) ⋅ g ( x + Δ x ) − g ( x ) Δ x \frac{\Delta y}{\Delta x} = \frac{f(g(x + \Delta x)) - f(g(x))}{g(x + \Delta x) - g(x)} \cdot \frac{g(x + \Delta x) - g(x)}{\Delta x} ΔxΔy=g(x+Δx)−g(x)f(g(x+Δx))−f(g(x))⋅Δxg(x+Δx)−g(x) - 极限过程:
当 Δ x → 0 \Delta x \to 0 Δx→0,我们有 Δ u → 0 \Delta u \to 0 Δu→0,因此: d y d x = lim Δ x → 0 ( f ( g ( x + Δ x ) ) − f ( g ( x ) ) g ( x + Δ x ) − g ( x ) ⋅ g ( x + Δ x ) − g ( x ) Δ x ) \frac{dy}{dx} = \lim_{\Delta x \to 0} \left( \frac{f(g(x + \Delta x)) - f(g(x))}{g(x + \Delta x) - g(x)} \cdot \frac{g(x + \Delta x) - g(x)}{\Delta x} \right) dxdy=Δx→0lim(g(x+Δx)−g(x)f(g(x+Δx))−f(g(x))⋅Δxg(x+Δx)−g(x))根据导数的定义,我们有: d y d x = ( lim Δ u → 0 Δ y Δ u ) ⋅ ( lim Δ x → 0 Δ u Δ x ) \frac{dy}{dx} = \left( \lim_{\Delta u \to 0} \frac{\Delta y}{\Delta u} \right) \cdot \left( \lim_{\Delta x \to 0} \frac{\Delta u}{\Delta x} \right) dxdy=(Δu→0limΔuΔy)⋅(Δx→0limΔxΔu) - 导数表示: d y d x = d y d u ⋅ d u d x \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} dxdy=dudy⋅dxdu其中, d y d u = lim Δ u → 0 Δ y Δ u \frac{dy}{du} = \lim_{\Delta u \to 0} \frac{\Delta y}{\Delta u} dudy=Δu→0limΔuΔy 和 d u d x = lim Δ x → 0 Δ u Δ x \frac{du}{dx} = \lim_{\Delta x \to 0} \frac{\Delta u}{\Delta x} dxdu=Δx→0limΔxΔu。
因此复合函数的导数可以表示为外层函数的导数乘以内层函数的导数。
可视化:
- g(x):定义了内层函数 sin ( x ) \sin(x) sin(x)。
- f(u):定义了外层函数 exp ( u ) \exp(u) exp(u)。
- g_prime(x) 和 f_prime(u):定义了对应的导数。
- h(x):复合函数 e sin ( x ) e^{\sin(x)} esin(x)。
- h_prime(x):复合函数的导数,使用链式法则 f ′ ( g ( x ) ) ⋅ g ′ ( x ) f'(g(x)) \cdot g'(x) f′(g(x))⋅g′(x)。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation# 定义两个函数及其导数
def g(x):return np.sin(x)def f(u):return np.exp(u)def g_prime(x):return np.cos(x)def f_prime(u):return np.exp(u)# 复合函数及其导数
def h(x):return f(g(x))def h_prime(x):return f_prime(g(x)) * g_prime(x)# 生成x的值
x = np.linspace(0, 2 * np.pi, 400)
y_g = g(x)
y_f = f(y_g)
y_h = h(x)# 初始化图形
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 12))# 绘制函数 g(x)
ax1.plot(x, y_g, label=r'$g(x) = \sin(x)$', color='blue')
ax1.set_title('Function $g(x)$')
ax1.set_xlabel('$x$')
ax1.set_ylabel('$g(x)$')
ax1.legend()# 绘制函数 f(u)
u = np.linspace(-1, 1, 400)
ax2.plot(u, f(u), label=r'$f(u) = e^{u}$', color='green')
ax2.set_title('Function $f(u)$')
ax2.set_xlabel('$u$')
ax2.set_ylabel('$f(u)$')
ax2.legend()# 绘制复合函数 h(x) = f(g(x))
ax3.plot(x, y_h, label=r'$h(x) = e^{\sin(x)}$', color='red')
ax3.set_title('Composite Function $h(x) = f(g(x))$')
ax3.set_xlabel('$x$')
ax3.set_ylabel('$h(x)$')
ax3.legend()plt.subplots_adjust(hspace=0.5)# 初始化点和切线
point1, = ax1.plot([], [], 'ro') # 点
tangent_line1, = ax1.plot([], [], 'r--') # 切线point2, = ax2.plot([], [], 'ro') # 点
tangent_line2, = ax2.plot([], [], 'r--') # 切线point3, = ax3.plot([], [], 'ro') # 点
tangent_line3, = ax3.plot([], [], 'r--') # 切线def init():point1.set_data([], [])tangent_line1.set_data([], [])point2.set_data([], [])tangent_line2.set_data([], [])point3.set_data([], [])tangent_line3.set_data([], [])return point1, tangent_line1, point2, tangent_line2, point3, tangent_line3def animate(i):x0 = i * 2 * np.pi / 100 # 从 0 开始,步长为 2π / 100y0_g = g(x0)y0_h = h(x0)# 绘制 g(x) 的点和切线slope_g = g_prime(x0)point1.set_data([x0], [y0_g])tangent_x1 = np.array([x0 - 0.5, x0 + 0.5])tangent_y1 = y0_g + slope_g * (tangent_x1 - x0)tangent_line1.set_data(tangent_x1, tangent_y1)# 绘制 f(g(x)) 的点和切线u0 = y0_gy0_f = f(u0)slope_f = f_prime(u0)point2.set_data([u0], [y0_f])tangent_x2 = np.array([u0 - 0.5, u0 + 0.5])tangent_y2 = y0_f + slope_f * (tangent_x2 - u0)tangent_line2.set_data(tangent_x2, tangent_y2)# 绘制 h(x) = f(g(x)) 的点和切线slope_h = h_prime(x0)point3.set_data([x0], [y0_h])tangent_x3 = np.array([x0 - 0.5, x0 + 0.5])tangent_y3 = y0_h + slope_h * (tangent_x3 - x0)tangent_line3.set_data(tangent_x3, tangent_y3)return point1, tangent_line1, point2, tangent_line2, point3, tangent_line3ani = animation.FuncAnimation(fig, animate, frames=100, init_func=init, blit=True)# 保存为gif
ani.save('chain_rule_animation.gif', writer='imagemagick')# 显示动画
plt.show()
相关文章:

计算神经网络中梯度的核心机制 - 反向传播(backpropagation)算法(1)
计算神经网络中梯度的核心机制 - 反向传播(backpropagation)算法(1) flyfish 链式法则在深度学习中的主要应用是在反向传播(backpropagation)算法中。 从简单的开始 ,文本说的就是链式法则 R …...

VUE实现简易购物车
主要是对基础的指令的使用,直接上代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0">&l…...

混沌工程——从捣乱的视角看系统稳定性
概念 混沌工程是通过捣乱实验探究系统稳定性的实践过程,其作战武器是风险因子,即在健康的运行环境中引入风险变量来验证系统对风险的抵抗能力,它的作用是推动系统容错能力建设、验证监控告警及时性、提升研发问题排查能力。 混沌工程的工作…...

Windows宝塔面板部署ThinkPHP8.0创建Vue项目案例
安装ThinkPHP8.0 登录宝塔面板,创建一个站点。 输入composer代码,执行完成后自动创建TP目录 composer create-project topthink/think tp 网站目录设置为tp,运行目录设置为public 设置PHP版本为8.0以上,不然会出现下面的报错代…...

5G频段简介
5G频段 5G网络一共有29个频段,主要被分为两个频谱范围,其中6GHz以下的频段共有26个(统称为Sub6GHz),毫米波频段有3个。目前国内主要使用的是Sub6GHz,包括n1/n3/n28/n41/n77/n78/n79共7个频段。具体介绍如下…...

【python学习】bytearray 数组
在Python中,bytearray 是一个可变序列,用于表示一个字节数组。与不可变的 bytes 类型相比,bytearray 允许你修改其内容。你可以通过索引来访问和修改 bytearray 中的元素,也可以添加或删除元素。 使用 bytearray 的一些示例&…...

Labview_Occurrencel(事件发生)
PS:这里遇到 一个很Low的事情: 在停止第二个while循环的时候出现了停止不了的情况。因为等待事件发生设置的超时时间为:-1。所以等事件发生后出现了条件接线端已经执行的情况,所以当下次事件发生时未能及时停止。初版的停止设置如下图&#x…...
天气网站爬虫及可视化
摘要:随着互联网的快速发展,人们对天气信息的需求也越来越高。本论文基于Python语言,设计并实现了一个天气网站爬虫及可视化系统。该系统通过网络爬虫技术从多个天气网站上获取实时的天气数据,并将数据进行清洗和存储。同时&#…...

【python - 数据】
一、序列 序列(sequence)是一组有顺序的值的集合,是计算机科学中的一个强大且基本的抽象概念。序列并不是特定内置类型或抽象数据表示的实例,而是一个包含不同类型数据间共享行为的集合。也就是说,序列有很多种类&…...

几种热管的构造
1、超薄热管构造形式 在实际应用中,超薄热管通常定义为厚度小于2.0mm的平板热管。超薄热管很薄,可紧贴电子元件表面散热,故被广泛应用于移动和可携带电子设备,如智能手机、笔记本电脑和智能手表。用于笔记本电脑和平板电脑的超薄…...
【GitOps】使用Google工具JIB实现本地无需安装容器推送镜像,加速SpringCloud项目开发
文章目录 一、效果展示二、简介三、安装Jib插件1、区分环境2、安装插件一、效果展示 本地是window系统,无docker环境,没有任何runtime,使用jib工具打包镜像并推送完成,用时20秒 二、简介 Jib 是 Google 开发的一款开源工具,旨在帮助 Java 开发者更高效地将 Java 应用程…...
【proteus经典实战】16X192点阵程序
一、简介 6X192点阵程序通常用于表示高分辨率图像或文字,其中16X表示像素阵列的宽度,192表示每个像素阵列中的点阵数,16X192点阵程序需要一定的编程知识和技能才能编写和调试,同时还需要考虑硬件设备的兼容性和性能等因素。 初始…...
小白上手AIGC-基于FC部署stable-diffusion
AIGC AIGC(人工智能创造内容)作为一种基于人工智能技术生成内容的新型创作模式。打破了过去大家对于AI的理解都是说只能涉足部分领域而无法涉足艺术或者是其他的创作领域的定律,现在的AIGC也能够创作内容了,而不再只是单纯的返回…...

一些指标的学习
1.平均倒数排名(MRR) 1.定义 MRR 是衡量检索系统返回的结果列表中第一个相关结果位置的指标。具体来说,它是所有查询倒数排名的平均值。 2.计算步骤 对每个查询,找到第一个正确答案在结果列表中的排名 𝑅ᵄ…...
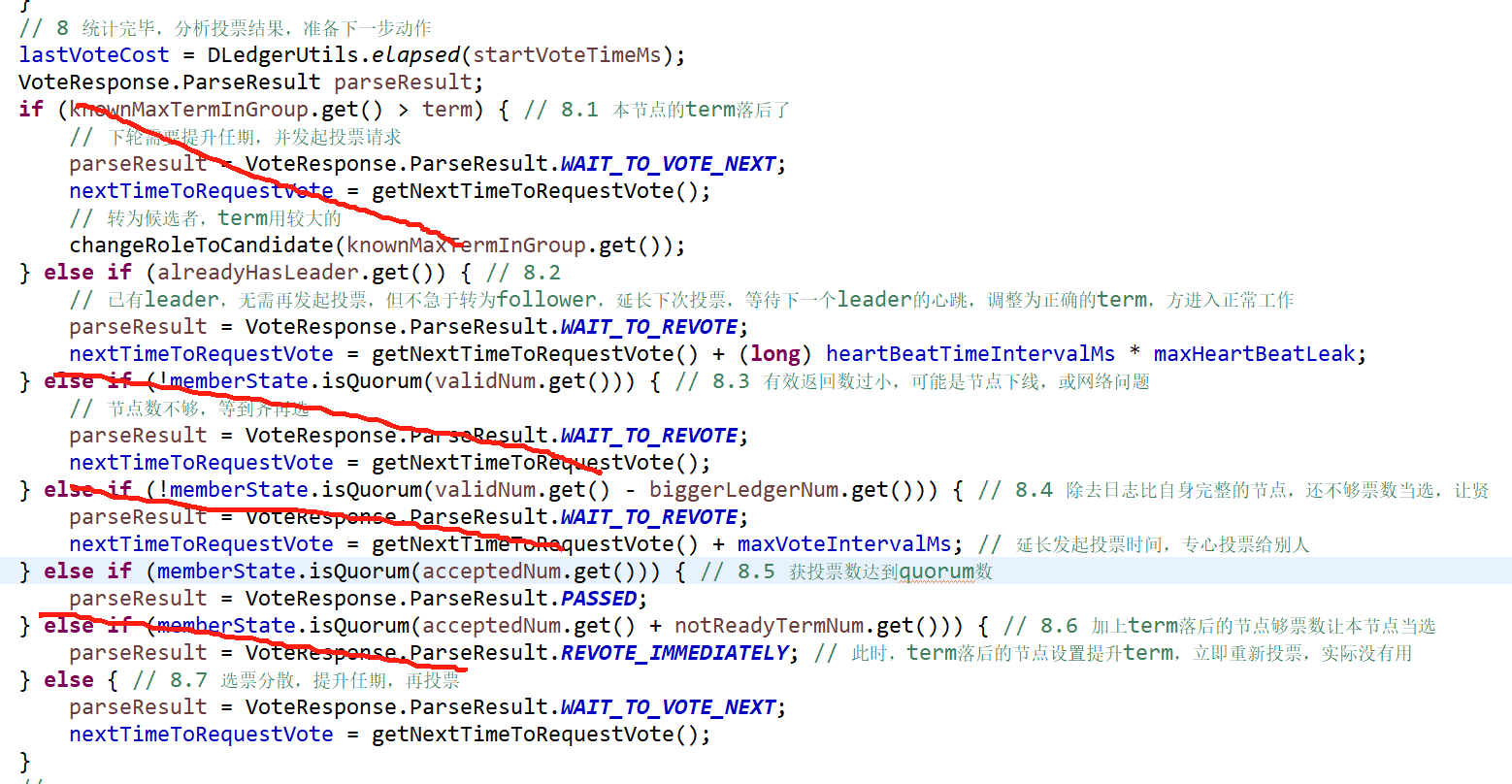
dledger原理源码分析系列(三)-选主
简介 dledger是openmessaging的一个组件, raft算法实现,用于分布式日志,本系列分析dledger如何实现raft概念,以及dledger在rocketmq的应用 本系列使用dledger v0.40 本文分析dledger的选主 关键词 Raft Openmessaging 心跳/选…...

如何修改PDF文档的作者名称?
要修改一个 PDF 文档的作者名称,你可以按照以下步骤进行操作: 1. **使用 Adobe Acrobat**(如果有): - Adobe Acrobat 是一个功能强大的 PDF 编辑工具,支持修改文档属性信息,包括作者名称。打开…...
从笔灵到AI去痕:全方位提升内容创作与学术诚信
内容为王,在内容创作的世界中尤为重要。然而,面对写作时常常感到无从下手:有时缺乏灵感,有时难以表达清楚自己的想法。AI写作助手的出现,为这些问题提供了创新的解决方案,极大地改变了内容创作的过程。 今…...

考试如果出现汉诺塔问题怎么办?
对于这道题来说 就按照测试案例里的数字进行输入 测试案例用100 那这三只鸡的具体最多能有多少只鸡呢? 用总数除以这只鸡的单价>>>>>>>即为这只鸡最多有 >>>>>>>> n / 单价 修改后 >>>>> 不只适…...

导出word模板开发记录
exportWordDocx.js import JSZipUtils from “jszip-utils” import Docxtemplater from “docxtemplater” import {saveAs} from “file-saver” import PizZip from “pizzip” const exportWordDocx (demoUrl, docxData, fileName) > {// 读取并获得模板文件的二进制…...

PHP爬虫类的并发与多线程处理技巧
PHP爬虫类的并发与多线程处理技巧 引言: 随着互联网的快速发展,大量的数据信息存储在各种网站上,获取这些数据已经成为很多业务场景下的需求。而爬虫作为一种自动化获取网络信息的工具,被广泛应用于数据采集、搜索引擎、舆情分析…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
