Day38:LeedCode 1049. 最后一块石头的重量 II 494. 目标和 474.一和零
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40] 输出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
思路:本题和Day42:动态规划 LeedCode 01背包 416. 分割等和子集-CSDN博客
中的分割等和子集类似,其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了
动态规划:
1.确定dp数组以及下标的含义
dp[i]:容量为i的背包,能背的最大重量
相对于 01背包,本题中,石头的重量是 stones[i],石头的价值也是 stones[i]
2.确定递推公式
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3.dp数组如何初始化
dp[j]都初始化为0
4.确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历
最后dp[target]里是容量为target的背包所能背的最大重量。
5.举例推导
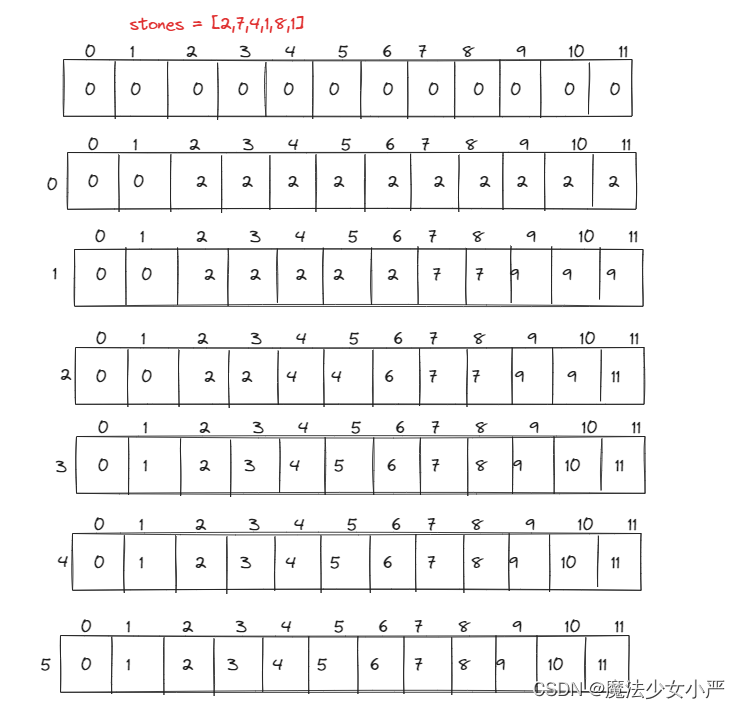
class Solution {public int lastStoneWeightII(int[] stones) {int length=stones.length;int target=0;int sums=0;for(int i=0;i<stones.length;i++){sums+=stones[i];}target=sums/2;int[] dp=new int[target+1];for(int i=0;i<length;i++){for(int j=target;j>=0;j--){if(j>=stones[i]){dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);}}}return sums-dp[target]-dp[target];}
}注意:在计算target的时候,target = sum / 2 因为是向下取整,所以sum - dp[target] 一定是大于等于dp[target]的。
494. 目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
思路:
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,装满容量为x的背包,有几种方法。
由于数组中的数都是整数,所以加法总和x一定是整数,如果(target + sum) / 2不是整数,意味着无解,return 0
与此同时,如果target的绝对值已经大于sum,那么也是没有方案的。
动态规划:
1.确定dp数组以及下标的含义
dp[i][j] 表示:用[0,i]的数,填满j(包括j)这么大容积的包,有dp[i][j]种方法
2.确定递推公式
得到nums[i],凑成dp[i][j]就有dp[i-1][j-nums[i]] 种方法。
没有用到nums[i],凑出凑成dp[i][j]就有dp[i-1][j]种方法。
故:dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]];
3.dp数组如何初始化
nums[i]!=0时:在初始化的时候dp[i][0]一定要初始化为1,凑出和为0的有1种方法
nums[i]==0时:在初始化的时候dp[i][0]一定要初始化为1,凑出和为0的有2种方法
4.确定遍历顺序
dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]];由递推公式可知从上往下遍历
5.举例推导
代码参考:
二维数组
class Solution {public int findTargetSumWays(int[] nums, int target) {int sums=0;for(int i=0;i<nums.length;i++){sums+=nums[i];}int x=(sums+target)/2;if((sums+target)%2==1)return 0;if(Math.abs(target)>sums) return 0;int[][] dp=new int[nums.length][x+1];//初始化for(int i=0;i<nums.length;i++){dp[i][0]=1;}for(int i=0;i<=x;i++){if(i==nums[0]){dp[0][i]+=1;}}for(int i=1;i<nums.length;i++){for(int j=0;j<=x;j++){if(j>=nums[i]){dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]];}else{dp[i][j]=dp[i-1][j];}}}return dp[nums.length-1][x];}
}一维数组:
class Solution {public int findTargetSumWays(int[] nums, int target) {int sums=0;for(int i=0;i<nums.length;i++){sums+=nums[i];}int x=(sums+target)/2;if((sums+target)%2==1)return 0;if(Math.abs(target)>sums) return 0;int[] dp=new int[x+1];//初始化dp[0]=1;for(int i=0;i<nums.length;i++){for(int j=x;j>=nums[i];j--){dp[j]=dp[j]+dp[j-nums[i]]; }}return dp[x];}
}相关文章:

Day38:LeedCode 1049. 最后一块石头的重量 II 494. 目标和 474.一和零
1049. 最后一块石头的重量 II 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果…...

sqlalchemy分页查询
sqlalchemy分页查询 在SQLAlchemy中,可以使用limit和offset方法实现分页查询 from sqlalchemy.orm import sessionmaker from sqlalchemy import create_engine from models import MyModel # 假设MyModel是你定义的模型# 连接数据库 engine = create_engine(sqlite:///myd…...

Java--常用类APl(复习总结)
前言: Java是一种强大而灵活的编程语言,具有广泛的应用范围,从桌面应用程序到企业级应用程序都能够使用Java进行开发。在Java的编程过程中,使用标准类库是非常重要的,因为标准类库提供了丰富的类和API,可以简化开发过…...

【股指期权投教】一手股指期权大概多少钱?
一手股指期权的权利金大概在几千人民币左右,如果是作为期权卖方还需要另外缴纳保证金的。国内的股指期权有三种,沪深300、上证50、中证1000股指期权,每点合约人民币100 元。 期权合约的价值计算可以通过此公式得出:权利金的支付或…...
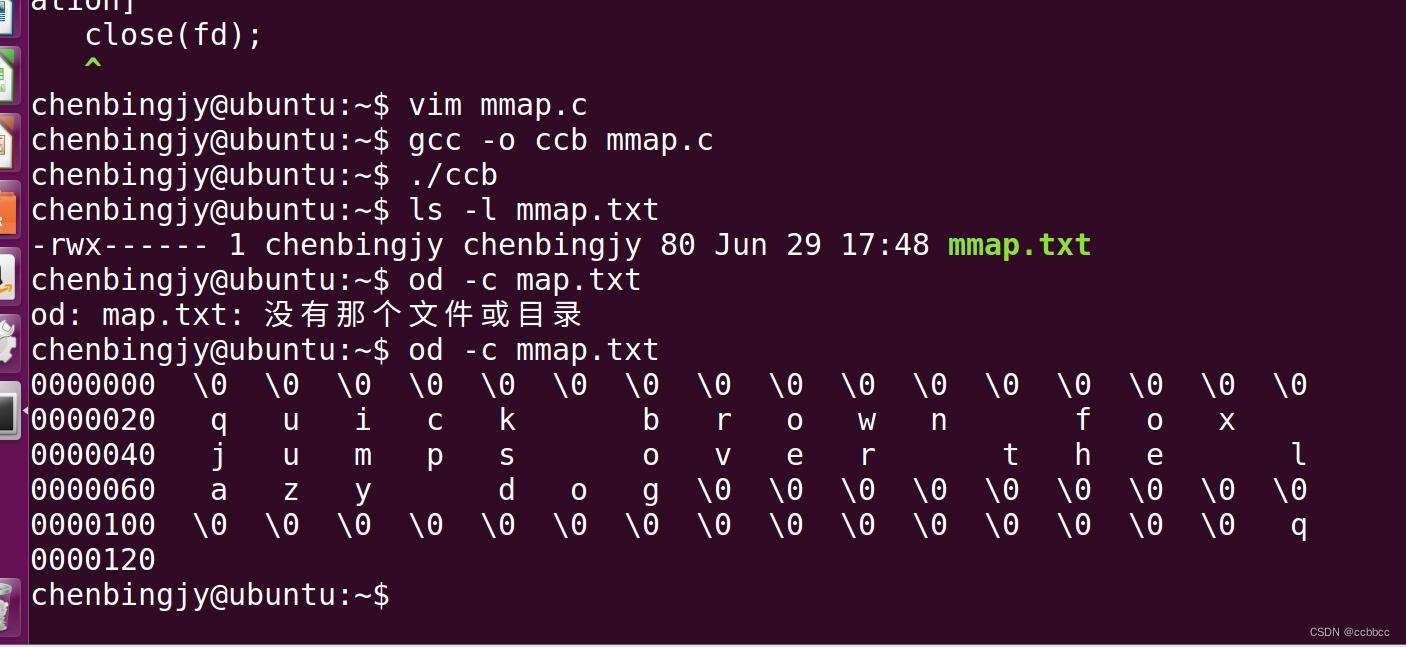
mmap()函数和munmap()函数的例子
代码: #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <sys/mman.h> #include <string.h> #include <stdio.h> #include <unistd.h>#define FILELENGTH 80 int main(void) {int fd-1;char …...

计算神经网络中梯度的核心机制 - 反向传播(backpropagation)算法(1)
计算神经网络中梯度的核心机制 - 反向传播(backpropagation)算法(1) flyfish 链式法则在深度学习中的主要应用是在反向传播(backpropagation)算法中。 从简单的开始 ,文本说的就是链式法则 R …...

VUE实现简易购物车
主要是对基础的指令的使用,直接上代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0">&l…...

混沌工程——从捣乱的视角看系统稳定性
概念 混沌工程是通过捣乱实验探究系统稳定性的实践过程,其作战武器是风险因子,即在健康的运行环境中引入风险变量来验证系统对风险的抵抗能力,它的作用是推动系统容错能力建设、验证监控告警及时性、提升研发问题排查能力。 混沌工程的工作…...

Windows宝塔面板部署ThinkPHP8.0创建Vue项目案例
安装ThinkPHP8.0 登录宝塔面板,创建一个站点。 输入composer代码,执行完成后自动创建TP目录 composer create-project topthink/think tp 网站目录设置为tp,运行目录设置为public 设置PHP版本为8.0以上,不然会出现下面的报错代…...

5G频段简介
5G频段 5G网络一共有29个频段,主要被分为两个频谱范围,其中6GHz以下的频段共有26个(统称为Sub6GHz),毫米波频段有3个。目前国内主要使用的是Sub6GHz,包括n1/n3/n28/n41/n77/n78/n79共7个频段。具体介绍如下…...

【python学习】bytearray 数组
在Python中,bytearray 是一个可变序列,用于表示一个字节数组。与不可变的 bytes 类型相比,bytearray 允许你修改其内容。你可以通过索引来访问和修改 bytearray 中的元素,也可以添加或删除元素。 使用 bytearray 的一些示例&…...

Labview_Occurrencel(事件发生)
PS:这里遇到 一个很Low的事情: 在停止第二个while循环的时候出现了停止不了的情况。因为等待事件发生设置的超时时间为:-1。所以等事件发生后出现了条件接线端已经执行的情况,所以当下次事件发生时未能及时停止。初版的停止设置如下图&#x…...
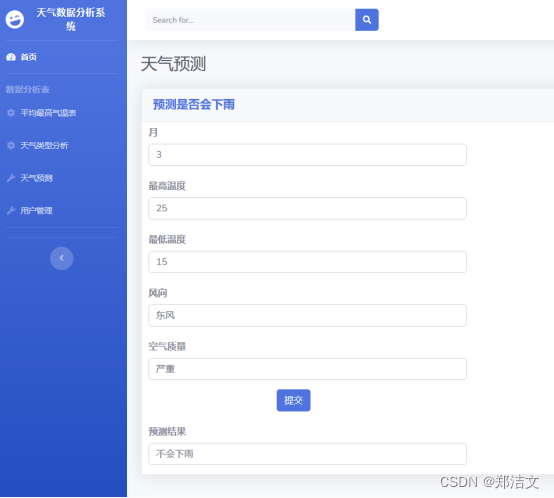
天气网站爬虫及可视化
摘要:随着互联网的快速发展,人们对天气信息的需求也越来越高。本论文基于Python语言,设计并实现了一个天气网站爬虫及可视化系统。该系统通过网络爬虫技术从多个天气网站上获取实时的天气数据,并将数据进行清洗和存储。同时&#…...

【python - 数据】
一、序列 序列(sequence)是一组有顺序的值的集合,是计算机科学中的一个强大且基本的抽象概念。序列并不是特定内置类型或抽象数据表示的实例,而是一个包含不同类型数据间共享行为的集合。也就是说,序列有很多种类&…...

几种热管的构造
1、超薄热管构造形式 在实际应用中,超薄热管通常定义为厚度小于2.0mm的平板热管。超薄热管很薄,可紧贴电子元件表面散热,故被广泛应用于移动和可携带电子设备,如智能手机、笔记本电脑和智能手表。用于笔记本电脑和平板电脑的超薄…...
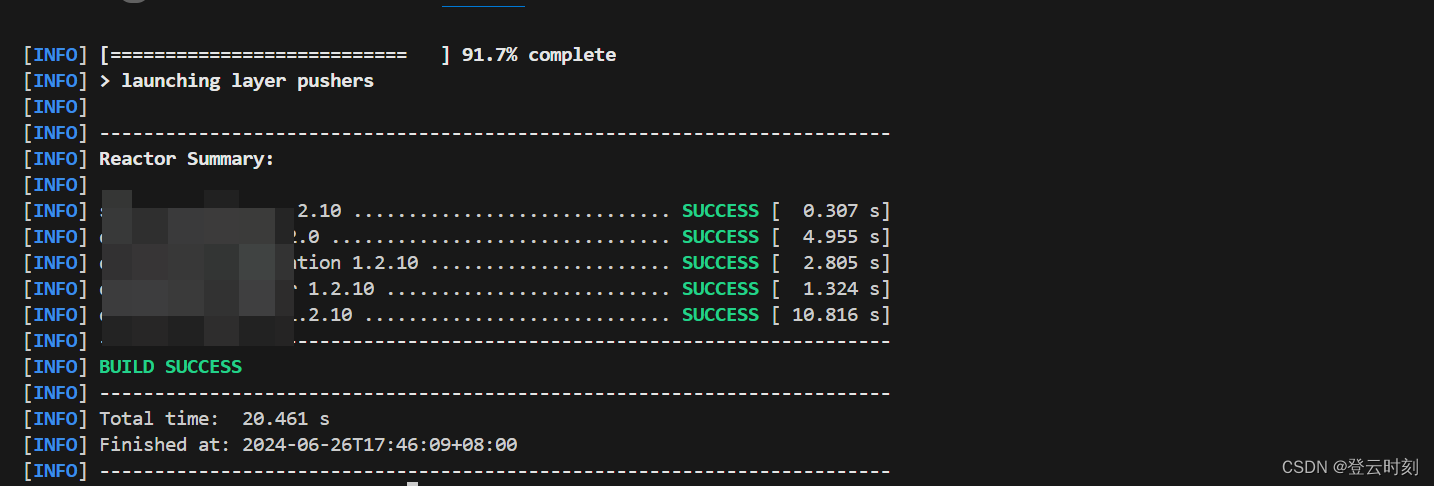
【GitOps】使用Google工具JIB实现本地无需安装容器推送镜像,加速SpringCloud项目开发
文章目录 一、效果展示二、简介三、安装Jib插件1、区分环境2、安装插件一、效果展示 本地是window系统,无docker环境,没有任何runtime,使用jib工具打包镜像并推送完成,用时20秒 二、简介 Jib 是 Google 开发的一款开源工具,旨在帮助 Java 开发者更高效地将 Java 应用程…...
【proteus经典实战】16X192点阵程序
一、简介 6X192点阵程序通常用于表示高分辨率图像或文字,其中16X表示像素阵列的宽度,192表示每个像素阵列中的点阵数,16X192点阵程序需要一定的编程知识和技能才能编写和调试,同时还需要考虑硬件设备的兼容性和性能等因素。 初始…...
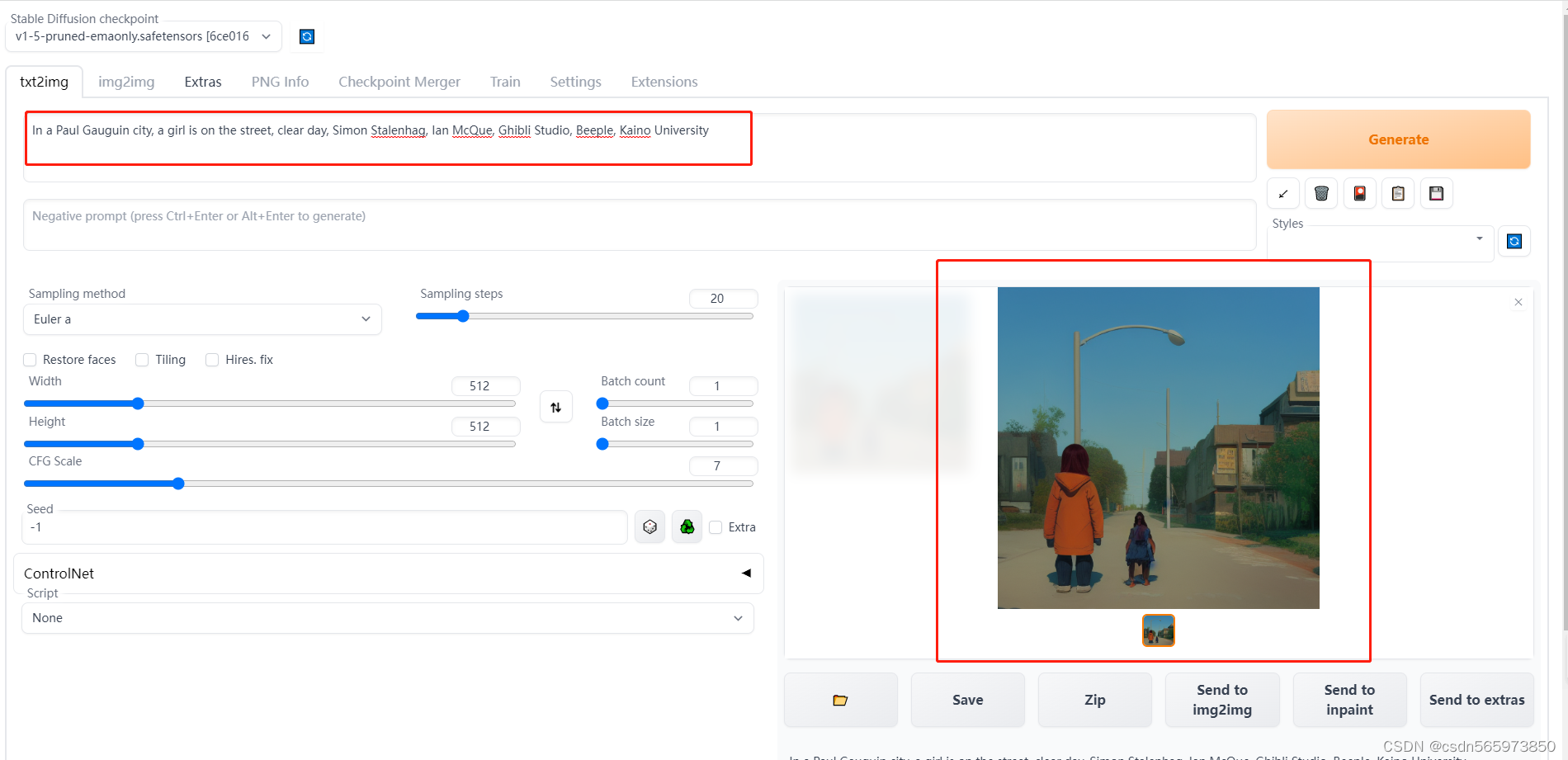
小白上手AIGC-基于FC部署stable-diffusion
AIGC AIGC(人工智能创造内容)作为一种基于人工智能技术生成内容的新型创作模式。打破了过去大家对于AI的理解都是说只能涉足部分领域而无法涉足艺术或者是其他的创作领域的定律,现在的AIGC也能够创作内容了,而不再只是单纯的返回…...

一些指标的学习
1.平均倒数排名(MRR) 1.定义 MRR 是衡量检索系统返回的结果列表中第一个相关结果位置的指标。具体来说,它是所有查询倒数排名的平均值。 2.计算步骤 对每个查询,找到第一个正确答案在结果列表中的排名 𝑅ᵄ…...
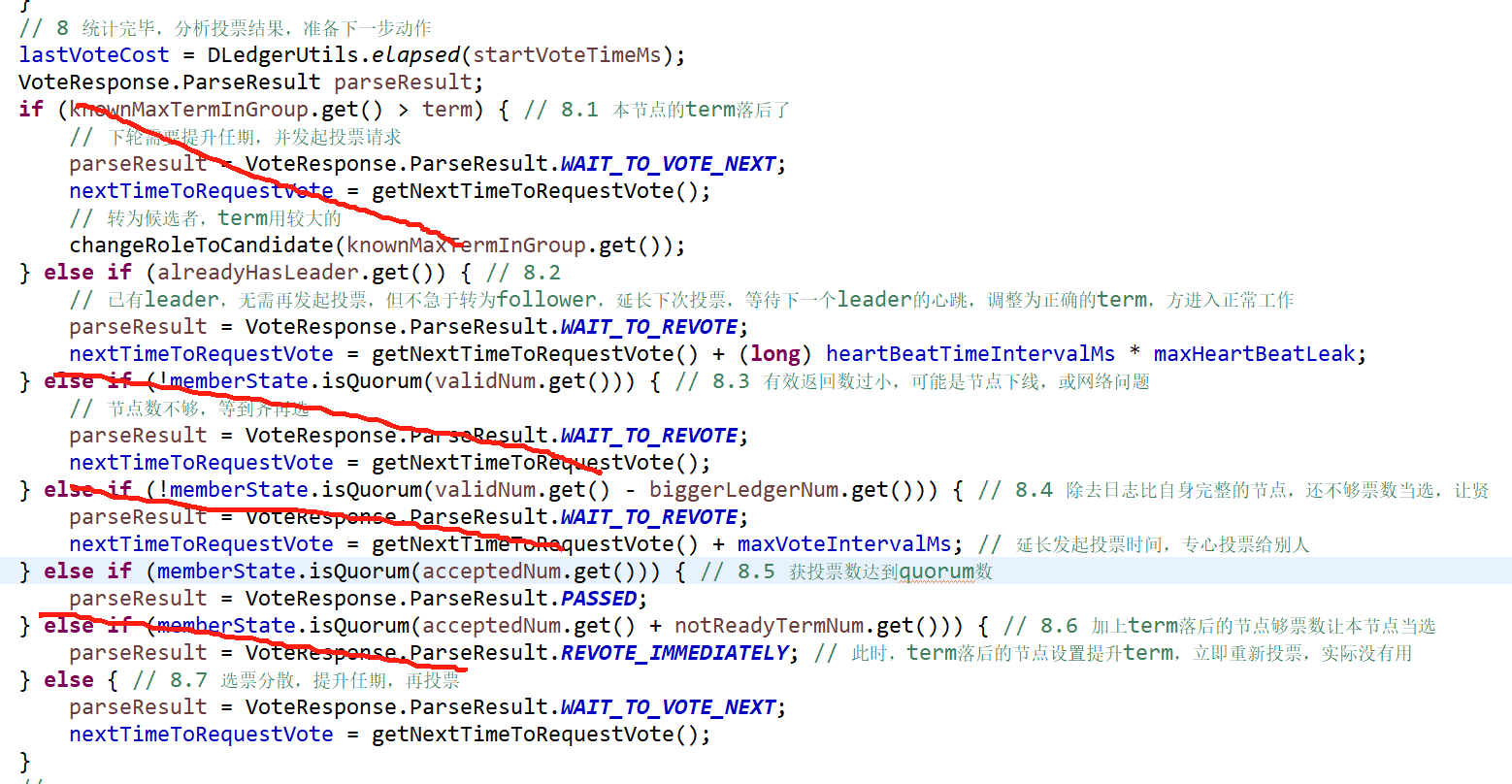
dledger原理源码分析系列(三)-选主
简介 dledger是openmessaging的一个组件, raft算法实现,用于分布式日志,本系列分析dledger如何实现raft概念,以及dledger在rocketmq的应用 本系列使用dledger v0.40 本文分析dledger的选主 关键词 Raft Openmessaging 心跳/选…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
