三阶魔方公式详解及快速解法方法介绍
三阶魔方公式详解及快速解法方法介绍
大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来深入探讨三阶魔方的公式及其快速解法方法。无论是初学者还是已经熟练的玩家,掌握这些公式和方法都能帮助你更快速地解决魔方。
什么是三阶魔方?
三阶魔方,又称魔方或魔方立方体,是一种立方体拼图玩具,由于其外观有六个面,每个面有一个颜色,通过旋转魔方块,使得每个面的所有小块都是同一种颜色。三阶魔方的标准尺寸为3x3x3,即每个面有9块。
魔方的解法方法
解决三阶魔方的方法可以分为多种,其中包括公式法和层次法。公式法通过记忆和应用一系列特定的旋转公式来逐步还原魔方,而层次法则是将魔方分解成一系列层次来解决。
Java代码中的魔方解法
在Java中,我们可以模拟魔方的旋转和解决过程。以下是一个简单的示例,展示了如何使用Java代码表示魔方状态并应用基本的旋转公式来实现解决过程。
package cn.juwatech.cube;public class RubiksCubeSolver {// 假设魔方表示为一个3x3的二维数组,每个元素代表一个小块的颜色或编号private int[][] cube;// 构造函数初始化魔方public RubiksCubeSolver() {this.cube = new int[3][3]; // 用数字或颜色表示每个块// 初始化魔方状态...}// 示例:实现一个旋转魔方的方法,例如顺时针旋转顶层public void rotateTopClockwise() {// 顶层顺时针旋转的算法实现...}// 其他旋转方法,根据需求实现各种公式和操作
}public class RubiksCubeMain {public static void main(String[] args) {RubiksCubeSolver solver = new RubiksCubeSolver();// 初始化魔方状态...// 调用旋转方法进行解法示例solver.rotateTopClockwise();// 其他操作和解法步骤...}
}
常用的三阶魔方公式
1. 顶层旋转公式
- 顶层顺时针旋转: U, U’, U2
- 顶层逆时针旋转: U’, U, U2
2. 底层旋转公式
- 底层顺时针旋转: D, D’, D2
- 底层逆时针旋转: D’, D, D2
3. 中层旋转公式
- 中层顺时针旋转: M, M’, M2
- 中层逆时针旋转: M’, M, M2
快速解法方法
快速解法方法包括基于层次法的CFOP方法(Cross, F2L, OLL, PLL)和基于公式法的LBL方法(Layer by Layer)。这些方法通过预先设定的步骤和公式来快速还原魔方,需要玩家多次练习和记忆公式才能熟练掌握。
结论
通过本文的介绍,我们详细探讨了三阶魔方的公式及其快速解法方法。魔方不仅是一款有趣的玩具,更是一种锻炼逻辑思维和解决问题能力的工具。
相关文章:

三阶魔方公式详解及快速解法方法介绍
三阶魔方公式详解及快速解法方法介绍 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来深入探讨三阶魔方的公式及其快速解法方法。无论是初学者还是已经…...
)
前端的拖拽和缩放(缩放以鼠标为中心)
效果: 拖拽和缩放(缩放以鼠标为中心) 代码具体实现如下: 但是有几个注意点 (1)为什么需要设置 transform-origin: 0 0; 缩放时以鼠标为中心进行缩放。这意味着需要手动计算缩放过程中元素的位移&#…...

【Vue】单向和双向数据绑定
在 Vue.js 中,数据绑定可以分为单向数据绑定和双向数据绑定两种类型。 单向数据绑定 单向数据绑定是指数据从模型流向视图,即数据的变化会自动反映到视图中,但视图中的变化不会自动反映回模型。Vue.js 中的单向数据绑定主要通过以下方式实现…...
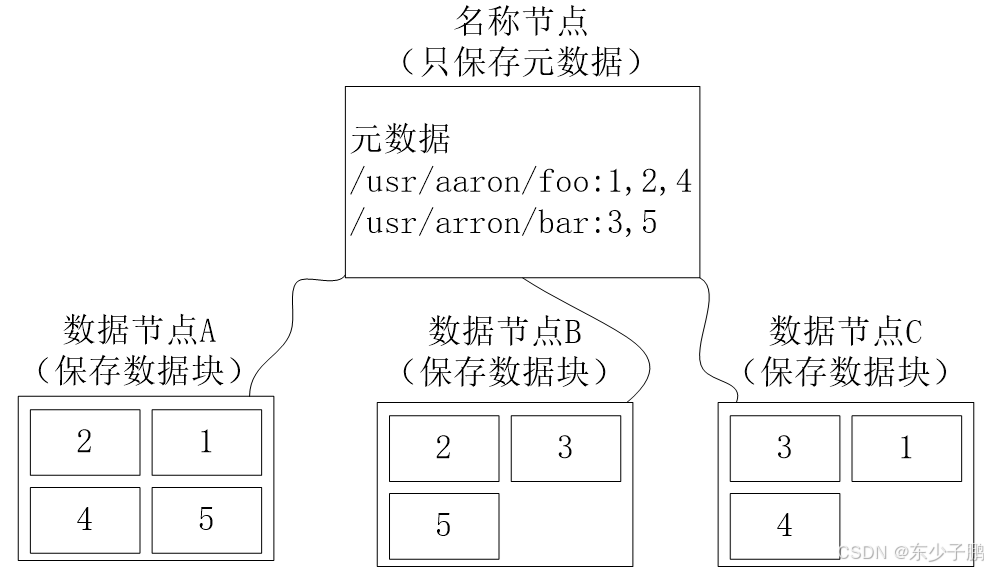
HDFS学习
3.5 HDFS存储原理 3.5.1 冗余数据保存 作为一个分布式文件系统,为了保证系统的容错性和可用性,HDFS采用了多副本方式对数据进行冗余存储,通常一个数据块的多个副本会被分布到不同的数据节点上。 如图所示,数据块1被分别存放到…...
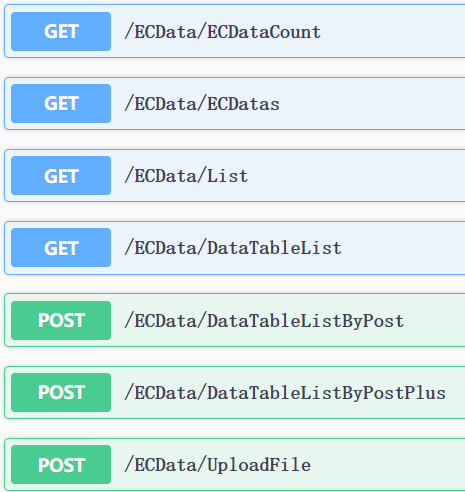
Winform使用HttpClient调用WebApi的基本用法
Winform程序调用WebApi的方式有很多,本文学习并记录采用HttpClient调用基于GET、POST请求的WebApi的基本方式。WebApi使用之前编写的检索环境检测数据的接口,如下图所示。 调用基于GET请求的无参数WebApi 创建HttpClient实例后调用GetStringAsync函数获…...
python–基础篇–正则表达式–是什么
文章目录 定义一:正则表达式就是记录文本规则的代码定义一:正则表达式是一个特殊的字符序列,用于判断一个字符串是否与我们所设定的字符序列是否匹配,也就是说检查一个字符串是否与某种模式匹配。初识 Python 正则表达式 定义一&a…...

15 个适用于企业的生成式 AI 用例
作者:来自 Elastic Jennifer Klinger 关于生成式人工智能及其能做什么(和不能做什么)有很多讨论。生成式人工智能(例如大型语言模型 - LLMs)利用从大量训练数据中学习到的模式和结构来创建原创内容,而无需存…...

若依框架中组件使用教程
...

秋招力扣刷题——数据流的中位数
一、题目要求 中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。 例如 arr [2,3,4] 的中位数是 3 。 例如 arr [2,3] 的中位数是 (2 3) / 2 2.5 。 实现 MedianFinder 类: MedianFinder() 初始化 …...
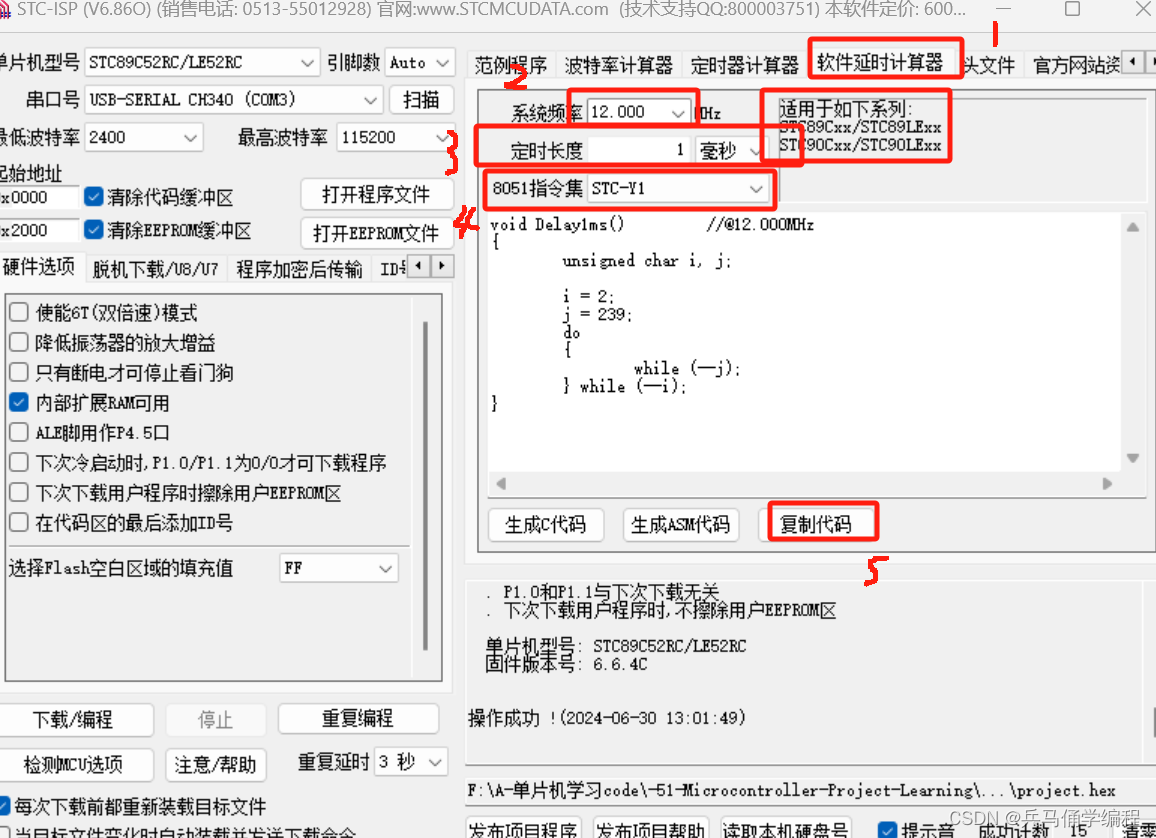
51单片机学习——LED功能一系列实现
目录 一、开发前准备 二、点亮LED 三、LED闪烁 四、LED流水灯 五、LED流水灯plus 一、开发前准备 开发工具软件 烧录软件 其次还需要一块51单片机学习开发板及原理图 keil创造project文件及开启生成.hex文件 二、点亮LED 看二位进制对照原理图; #include <…...

互联网大厂核心知识总结PDF资料
我们要敢于追求卓越,也能承认自己平庸,不要低估3,5,10年沉淀的威力 hi 大家好,我是大师兄,大厂工作特点是需要多方面的知识和技能。这种学习和积累一般人需要一段的时间,不太可能一蹴而就&…...

设计模式-状态模式和策略模式
1.状态模式 1.1定义 当一个对象的内在状态改变时允许根据当前状态作出不同的行为; 1.2 适用场景 (1)一个对象的行为取决于它的状态,并且它必须在运行时根据状态来决定其行为. (2)代码中包含了大量的与状态有关的条件语句,例如:一个操作含有庞大的多分值语句(if…...
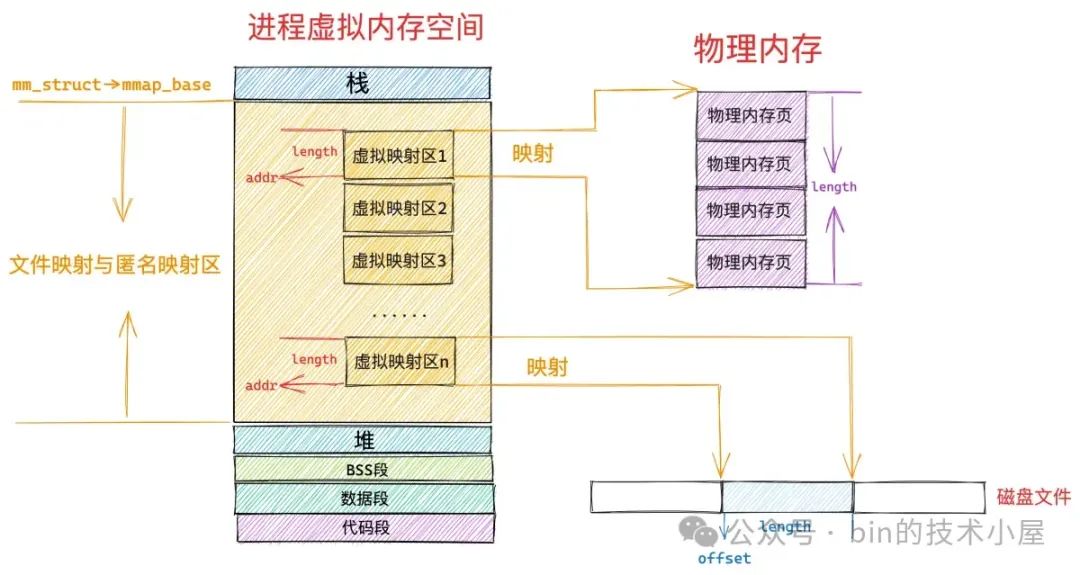
Java NIO Buffer概念
针对每一种基本类型的 Buffer ,NIO 又根据 Buffer 背后的数据存储内存不同分为了:HeapBuffer,DirectBuffer,MappedBuffer。 HeapBuffer 顾名思义它背后的存储内存是在 JVM 堆中分配,在堆中分配一个数组用来存放 Buffe…...

Kubernetes在Java应用部署中的最佳实践
Kubernetes在Java应用部署中的最佳实践 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Java应用程序中使用Kubernetes进行最佳部署实践。K…...

IOS Swift 从入门到精通:@escaping 和PreferenceKey
@escaping 在Swift中,@escaping是一个属性关键字,用于标记闭包参数。当一个闭包在函数返回之后才被调用时,这个闭包被称为逃逸闭包(Escaping Closure)。使用@escaping关键字可以告诉Swift编译器,传递给函数的闭包可能会在函数执行完毕后被调用,因此它需要“逃逸”函数的…...
基于PHP技术的校园论坛设计的设计与实现-计算机毕业设计源码08586
摘 要 本项目旨在基于PHP技术设计与实现一个校园论坛系统,以提供一个功能丰富、用户友好的交流平台。该论坛系统将包括用户注册与登录、帖子发布与回复、个人信息管理等基本功能,并结合社交化特点,增强用户之间的互动性。通过利用PHP语言及其…...

开机弹窗缺失OpenCL.dll如何解决?分享5种靠谱的解决方法
在电脑使用过程中,我们可能会遇到一些错误提示,其中之一就是“开机提示找不到OpenCL.dll”。那么,这个错误提示到底是怎么回事呢?它又对电脑有什么影响?我们又该如何解决这个问题并预防OpenCL.dll再次丢失呢࿱…...

IIS 服务器安装SSL证书
IIS 服务器安装SSL证书 步骤一:准备好 SSL 证书 准备好.pfx 格式的证书文件。 步骤二:安装 SSL 证书 1、打开【开始】菜单,找到【管理工具】,打开【Internet 信息服务(IIS)管理器】。 2、单击服务器名…...

二叉树第二期:堆的实现与应用
若对树与二叉树的相关概念,不太熟悉的同学,可移置上一期博客 链接:二叉树第一期:树与二叉树的概念-CSDN博客 本博客目标:对二叉树的顺序结构,进行深入且具体的讲解,同时学习二叉树顺序结构的应用…...

python-求出 e 的值
[题目描述] 利用公式 e11/1!1/2!1/3!⋯1/𝑛!,求 e 的值,要求保留小数点后 10 位。输入: 输入只有一行,该行包含一个整数 n,表示计算 e 时累加到1/n!。输出: 输出只有一行,该行包含计…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
