刷算法Leetcode---7(二叉树篇)(前中后序遍历)
前言
本文是跟着代码随想录的栈与队列顺序进行刷题并编写的 代码随想录
好久没刷算法了,最近又开始继续刷,果然还是要坚持。
二叉树的题目比之前多了好多,就多分几次写啦~
这是力扣刷算法的其他文章链接:刷算法Leetcode文章汇总
二叉树篇(前中后序遍历)
(1)144.二叉树的前序遍历
①递归,先加入当前节点值,再递归左右子节点
②栈迭代,先获取当前节点值,注意右节点先入栈,左节点后入栈
③栈迭代,从根开始遍历左节点,取值并入栈,再取栈顶右节点重复
④Morris遍历,将左节点的最右节点(即p2)右指针指向根,不使用额外空间,实现左子树遍历完后就回到根遍历右子树。若p2右指针为空,代表该树(即p1)的左子树未遍历
核心思想:添加根p1的值(即为中),遍历左节点,左不空就添加指向根的指针并继续往左,左空就添加该节点值(即为左)并找右节点,若右节点不为根就作为新子树遍历(即为右),若为根就回到之前的树遍历右节点并添加
class Solution {private List<Integer> res;public List<Integer> preorderTraversal(TreeNode root) {res = new ArrayList<>();TreeNode p1 = root, p2 = new TreeNode();while(p1!=null){if(p1.left==null){res.add(p1.val);p1=p1.right;}else{p2=p1.left;while(p2.right!=null&&p2.right!=p1){p2=p2.right;}if(p2.right==null){p2.right=p1;res.add(p1.val);p1=p1.left;}else{p2.right=null;p1=p1.right;}}}return res;}
}(2)145.二叉树的后序遍历
①递归,先递归左右子节点,再加入当前节点值
②栈迭代,取栈头,左右节点依次入栈,栈头值头插到结果
③Morris遍历,核心思路还是创建一个右子树最后一个节点到根的指针,由于根节点最后添加,要实现一个左节点到最右节点添加的方法
核心思想:从根p1开始,左不空就添加指向根的指针并继续往左,左空就添加(即为左)并遍历右节点,右不为根就作为新树遍历左节点,右为p1就代表所有左节点遍历完,将p1左节点到p2的节点逆序添加(即为右+中),注意最后要将根到整棵树最右节点的路径逆序添加
class Solution {private List<Integer> res;public List<Integer> postorderTraversal(TreeNode root) {res = new ArrayList<>();TreeNode p1=root,p2=null;while(p1!=null){if(p1.left==null){p1=p1.right;}else{p2=p1.left;while(p2.right!=null&p2.right!=p1){p2=p2.right;}if(p2.right==null){p2.right=p1;p1=p1.left;}else{p2.right=null;addRightPath(p1.left);p1=p1.right;}}}addRightPath(root);return res;}private void addRightPath(TreeNode node){int p = res.size();while(node!=null){res.add(p,node.val);node=node.right;}}
}(3)94.二叉树的中序遍历
①递归,先递归左子树,再加入当前节点值,再递归右子树
②栈迭代,一直找到最左节点并依次入栈,此时栈顶值加入结果,并将右节点作为当前节点,当栈或当前节点都不空时进行循环(注意是或)
注意:由于中序遍历要将根节点记录的中间,没办法像前序或后序实现简洁的迭代,必须先将左子树遍历完
③Morris遍历,与之前遍历思路同,创建一个右子树最后一个节点到根的指针。先将左子树遍历完(即左)后再添加根节点(即中),再遍历右子树(即右)。
class Solution {private List<Integer> res;public List<Integer> inorderTraversal(TreeNode root) {res = new ArrayList<>();TreeNode p1=root,p2=null;while(p1!=null){if(p1.left==null){res.add(p1.val);p1=p1.right;}else{p2=p1.left;while(p2.right!=null&&p2.right!=p1){p2=p2.right;}if(p2.right==null){p2.right=p1;p1=p1.left;}else{p2.right=null;res.add(p1.val);p1=p1.right;}}}return res;}
}二叉树篇(前中后序遍历)总结
①区分三种遍历顺序,前序(根左右)中序(左根右)后序(左右根),指的是根的位置
②都有递归实现的方法,代码简洁易懂,只用注意根添加和左右子树递归的顺序即可
③都有迭代实现的方式,需要显式栈辅助。都可以先将左子树全遍历完再遍历右子树,需要两层while。其中前序和后序有较简洁的迭代,每次将左右节点按特定顺序入栈即可,而中序遍历一定要先遍历完左子树才行
④都有Morris遍历,特点在于将左节点的最右节点右指针指向根节点,从而实现左子树遍历完后回到根节点遍历右子树,节点添加顺序有不同。特别是后序遍历对最右路径节点的单独添加,最好自己调试一遍更容易理解
⑤一般来说能用递归实现,就能用栈实现,因为递归是隐式栈
⑥代码随想录中有一种二叉树的统一迭代法,对前中后序的迭代遍历使用几乎相同的算法,只修改栈的添加顺序,感兴趣可以看一下,我记不下来就没看
相关文章:
(前中后序遍历))
刷算法Leetcode---7(二叉树篇)(前中后序遍历)
前言 本文是跟着代码随想录的栈与队列顺序进行刷题并编写的 代码随想录 好久没刷算法了,最近又开始继续刷,果然还是要坚持。 二叉树的题目比之前多了好多,就多分几次写啦~ 这是力扣刷算法的其他文章链接:刷算法Leetcode文章汇总 …...

AliyunOS安装Node.js
方法1:dnf软件包安装工具自动安装 最方便的安装方式是通过系统的dnf工具,我测试使用的AliyunOS的版本是Alibaba Cloud Linux 3.2104,具体流程如下: dnf module list nodejs #列出服务器中可以使用的所有nodejs版本确定下来希望安…...

three.js - MeshPhongMaterial材质(实现玻璃水晶球效果)
1、概念 phong网格材质:Mesh - Phong - Material 一种用于具有镜面高光的光泽表面的材质。 它可以模拟,具有镜面高光的光泽表面,提供镜面反射效果。 MeshPhongMaterial: MeshPhongMaterial是一种基于Phong光照模型的材质&#…...

笔记本电脑安装CentOS
正文共:1234 字 24 图,预估阅读时间:2 分钟 前面我们对VPP进行了多次介绍(羡慕!大佬的VPP能达到180G性能,而我的却只有13.5G),可以发现他的很多优点,但是我们也可以发现它…...

ssh转发功能入门
端口转发概述 端口转发,能够将其他TCP端口的网络数据通过SSH链路转发,并且提供了ssh的加密和解密的服务。 ssh端口转发有如下这些优点: 提供了ssh的加密传输,利于安全能够突破防火墙限制 目前ssh端口转发有如下几种方式&#x…...

Listary(Windows 文件搜索工具)专业版值得购买吗?
说到经典的国货软件,有一款 Win 软件是一定绕不过去的。它就是知名的本地文件搜索工具 Listary! 便捷的文件搜索窗口;快捷操作的体验;与系统更匹配的外观设计;更智能的排序和更可靠的索引。 便捷的文件搜索窗口 紧凑…...

面试突击指南:Java基础面试题2
面向对象和集合 1. 面向对象和面向过程的区别 面向过程:面向过程的编程方式是分析解决问题的步骤,然后用函数把这些步骤一步一步地实现,并在使用的时候逐个调用。这种方式性能较高,因此在单片机和嵌入式开发中经常采用面向过程开发。 面向对象:面向对象的编程方式是把问…...
)
MySQL快速安装(mysql8.0.30区别之前yum安装)
目录 一.初始化环境并解压 二.创建程序用户管理 三.修改mysql目录和配置文件的权限 四.修改配置文件 五.设置环境变量,申明/宣告mysql命令便于系统识别 六.初始化数据库 七.设置系统识别,进行操作 八.初始化数据库密码 九.用户并设置密码 十.赋…...

俄罗斯防空系统
俄罗斯的S系列防空系统是一系列先进的地对空导弹系统,旨在防御各类空中威胁,包括飞机、无人机、巡航导弹和弹道导弹。以下是几种主要的S系列防空系统: 1. **S-300系统**: - **S-300P**:最早期的版本,用…...

文件上传漏洞---Pyload
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 本文重点从靶场案例分析文件上传漏洞常见的Pylod,本文演示靶场upload-labs 一.文件类型---Pyload 不同的文件对应不同的文件类型,后端代码通过限制特定的文件类型…...

应用案例 | 如何监测高价值货物在物流运输过程中受到的振动和冲击?全面保障货物安全
一、货物运输 不同种类的货物对运输的要求不同,钢铁、煤炭、矿石等大宗物资通常对运输要求较低,而电子产品、IT 产品、家电等高价值敏感类货物则更强调运输的安全性和时效性,往往希望能尽可能安全和快速送达这类货物,使之尽快进入…...
VMware17安装Ubuntu20版本-保姆级别
首先需要安装好VMware和Ubuntu20的镜像,在网上搜索Ubuntu镜像下载即可,最后选择国内镜像站下载,这样更快点,然后打开VMware。 1.创建虚拟机: 2.选择自定义: 3.默认,继续下一步: 4.选…...

初探Xcode工具
初探Xcode工具 Xcode是苹果公司为Mac OS X和iOS平台开发软件的集成开发环境(IDE)。作为苹果开发者的首选工具,Xcode提供了一系列强大的功能,帮助开发者设计、编写、调试和发布应用程序。本文将对Xcode进行初步探索,介…...

小迪安全v2023笔记 1-18
小迪安全v2023笔记 1-18 棱角社区 文章目录 1. 基础入门1. 正向shell与反向shell2. web应用3. 抓包,封包,协议,app,小程序,pc应用,web应用 2. 信息打点1. 常见信息获取2. 文件泄露3. 常见阻碍4. CDN绕过&a…...
RabbitMQ WEB管理端介绍
页面功能概览 Overview(概述)Connections(连接)Channels(通道)Exchanges(交换器)Queues(队列)Admin(用户管理)。 1. Overview(概述) 主要分为三部分 1.1 Queued messages(所有队列的消息情况) Ready:待消费的消息总数Unacked:待应…...

三阶魔方公式详解及快速解法方法介绍
三阶魔方公式详解及快速解法方法介绍 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来深入探讨三阶魔方的公式及其快速解法方法。无论是初学者还是已经…...
)
前端的拖拽和缩放(缩放以鼠标为中心)
效果: 拖拽和缩放(缩放以鼠标为中心) 代码具体实现如下: 但是有几个注意点 (1)为什么需要设置 transform-origin: 0 0; 缩放时以鼠标为中心进行缩放。这意味着需要手动计算缩放过程中元素的位移&#…...

【Vue】单向和双向数据绑定
在 Vue.js 中,数据绑定可以分为单向数据绑定和双向数据绑定两种类型。 单向数据绑定 单向数据绑定是指数据从模型流向视图,即数据的变化会自动反映到视图中,但视图中的变化不会自动反映回模型。Vue.js 中的单向数据绑定主要通过以下方式实现…...
HDFS学习
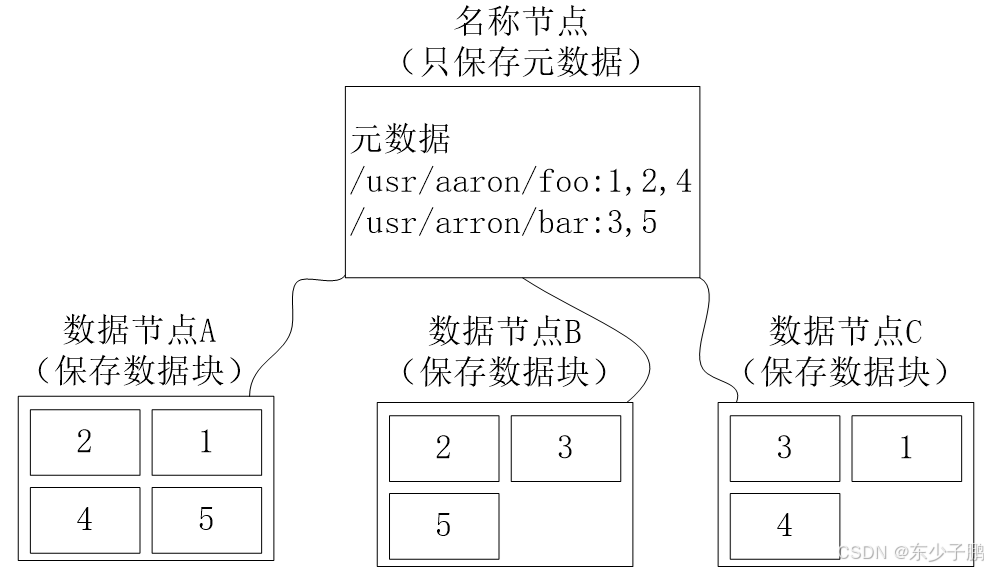
3.5 HDFS存储原理 3.5.1 冗余数据保存 作为一个分布式文件系统,为了保证系统的容错性和可用性,HDFS采用了多副本方式对数据进行冗余存储,通常一个数据块的多个副本会被分布到不同的数据节点上。 如图所示,数据块1被分别存放到…...
Winform使用HttpClient调用WebApi的基本用法
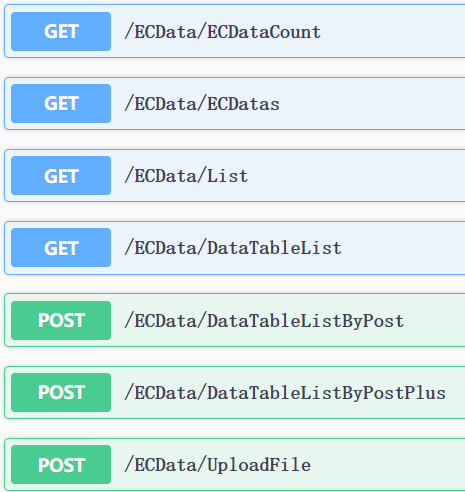
Winform程序调用WebApi的方式有很多,本文学习并记录采用HttpClient调用基于GET、POST请求的WebApi的基本方式。WebApi使用之前编写的检索环境检测数据的接口,如下图所示。 调用基于GET请求的无参数WebApi 创建HttpClient实例后调用GetStringAsync函数获…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
