简单多状态DP问题
这里写目录标题
- 什么是多状态DP
- 解决多状态DP问题应该怎么做?
- 关于多状态DP问题的几道题
- 1.按摩师
- 2.打家劫舍Ⅱ
- 3.删除并获得点数
- 4.粉刷房子
- 5.买卖股票的最佳时期含手冷冻期
- 总结

什么是多状态DP
多状态动态规划(Multi-State Dynamic Programming, Multi-State DP)问题是动态规划(DP)领域中的一个高级概念,涉及到在算法设计中引入多个状态来描述和解决复杂问题。与传统的单状态DP问题相比,多状态DP问题能够处理更多维度的状态信息,以应对更复杂的决策过程和状态转移关系。
以下是对多状态DP问题的详细介绍,包括定义、特点、常见应用场景和解决方法:
- 定义
多状态DP问题是指在动态规划算法中,引入了多个状态变量来描述一个问题的状态空间,并在这些状态之间进行转移来优化目标函数。每个状态变量通常代表了问题的一种不同的维度或特征,共同影响最终的决策过程。
简单定义:
在多状态DP问题中,我们使用一个或多个状态变量来描述问题的当前状态,并通过状态转移方程来找到从初始状态到目标状态的最优解。
- 特点
状态空间多维:与单状态DP不同,多状态DP问题中包含多个状态变量,每个状态变量可以是一个离散的值或者一个连续的范围。
状态转移复杂:状态之间的转移关系可能更加复杂,需要同时考虑多个维度的变化。
优化目标:目标通常是最小化或最大化一个函数,这个函数依赖于多个状态变量的组合。 - 常见应用场景
路径规划:如在地图上寻找从起点到终点的最短路径时,可以使用多个状态来描述不同的交通模式、时间限制等。
资源分配:如在生产计划中,考虑生产任务的时间、资源消耗、设备状态等多个因素来优化生产计划。
游戏设计:如在游戏中模拟复杂的状态变化,如角色的技能、装备状态、关卡进展等。
网络优化:如在网络流问题中,考虑多种流量限制、路由选择等因素来优化网络流量分配。 - 常见问题类型
以下是一些典型的多状态DP问题示例:
背包问题的扩展:如多维背包问题,其中不仅需要考虑物品的重量和价值,还需要考虑物品的其他特性(例如容量、数量限制等)。
序列比对:如生物信息学中的序列比对问题,涉及对比多个序列的不同状态(如基因序列的匹配和变异)。
多阶段决策问题:如多阶段投资决策,其中每个阶段的决策会影响后续阶段的状态。
解决多状态DP问题应该怎么做?
解决方法
解决多状态DP问题通常包括以下几个步骤:
- 定义状态变量:确定问题中的所有状态变量及其可能的取值范围。
- 构建状态转移方程:描述从一个状态转移到另一个状态的规则,通常包括状态之间的转移条件和代价。
- 设定初始状态和目标状态:确定动态规划的起始状态和目标状态,以及需要优化的目标函数。
- 编写DP递推公式:根据状态转移方程编写DP算法的递推公式。
- 实现DP算法:使用编程语言实现DP算法,并进行优化以提高算法的效率。
关于多状态DP问题的几道题
1.按摩师
题目链接
问题:
样例输出和输入:
这道题题意很简单一个按摩师,可以接收源源不断的预约请求,但是有一点他的预约请求不能在相邻的两天,意思就是我们看示例1,我们如果接受了1,那么就不能接受2,但是 可以接收3,3是可接受,但是不是一定要接受,最后让我们求预约的最长的时长的总和。
算法原理
状态表示:dp[i]表示到达i位置的最长预约时长。
状态转移方程 :这里我们想,到达i位置我们是不是有两种子状态,一种是预约,一种是不预约,如果预约话前一个i-1就不能预约,因为相邻的两个不能同时预约,所以我们将预约这种状态定义为f[i],将不预约这种状态定义为g[i],这里表示预约和不预约的最长预约时间。
所以这里第一种情况:当接受i位置的预约时,我们就不能接受i-1位置的预约,则f[i]可以表示为:f[i]=g[i-1]+nums[i]
第二种情况:当不接受i位置的值的时候,i-1位置可以选,可以不选,所以这里求选和不选的最大值,g[i]=max(g[i-1],f[i-1])
代码展示:
class Solution {
public:int massage(vector<int>& nums) {if(nums.size()==0){return 0;}//讨论两种情况,选或者不选int n = nums.size();vector<int> f(n), g(n);//初始化f[0] = nums[0], g[0] = 0;for (int i = 1;i < n;i++){f[i] = g[i - 1] + nums[i];g[i] = max(g[i - 1], f[i - 1]);}return max(g[n - 1], f[n - 1]);}
};
运行结果:
2.打家劫舍Ⅱ
题目链接
问题:
样例输出和输入:
这道题讲的是一个小偷,他要偷东西,但是不能偷相邻两个房间的东西,因为偷相邻两个房间的东西会触发报警器,还有一个要求就是不能同时偷头尾两个位置的东西,然后数组中的值代表房间的价值。最后让我们求可以偷到的最高价值。
算法原理:
这道题其实和打家劫舍1一样,只需要多一个判断,判断第一个位置是否偷,如果第一个位置偷,则第二个位置不能偷,如果 第一个位置不偷,则第二个位置可以偷 也可以不偷。
然后对可以偷的部分来一次打家劫舍1就可以了。
代码展示:
class Solution {
public:int rob(vector<int>& nums) {int n=nums.size();//三种情况当中偷最大的if(n==1){return nums[0];}if(n==2){return max(nums[0],nums[1]);}if(n==3){return max(max(nums[0],nums[1]),nums[2]);}//如果选第一个位置vector<int> f1(n),g1(n);f1[2]=nums[0]+nums[2],g1[2]=nums[0];for(int i=3;i<n-1;i++){f1[i]=g1[i-1]+nums[i];g1[i]=max(g1[i-1],f1[i-1]);}vector<int> f2(n),g2(n);f2[1]=nums[1],g2[1]=0;for(int i=2;i<n;i++){f2[i]=g2[i-1]+nums[i];g2[i]=max(g2[i-1],f2[i-1]);}return max(max(f1[n-2],g1[n-2]),max(g2[n-1],f2[n-1]));}
};
运行结果:

3.删除并获得点数
题目链接
问题:
样例输出和输入:
这道题让我们求的是最大点数,我们先看第一个例子,如果我们选了3,我们则不能选4和2,因为4和2不满足要求。如果我们选择4,我们则不能选择3但是我们可以选择2,这样最大的点数就是6
算法原理:
先对数组进行排序,升序数组利于我们跳过,然后再创建一个辅助数组,辅助数组的大小是原数组中最大的那个数加1,这个辅助数组的用途就是 存数组中的所有的数,如果 有相同的数则相加存起来,如果没有的话,则初始化为0.
状态表示:dp[i]表示i位置的当前获得的最大点数。。
状态转移方程:这里到达i位置的时候有两种情况,选或者不选,所以我们又需要两种状态来表示,这里选f[i],不选g[i],这里如果我们选第i个位置则前后位置都不能选则f[i]=g[i-1]+arr[i]如果我们不选i位置,则i-1位置可以选也可以不选,就是求选和不选的最大值:g[i]=max(g[i-1],f[i-1])。
代码展示:
class Solution {
public:int deleteAndEarn(vector<int>& nums) {sort(nums.begin(), nums.end());int n = nums.size();vector<int> arr(nums[n - 1]+1);for (int i = 0;i < nums.size();i++){arr[nums[i]] += nums[i];}vector<int> f(arr.size()), g(arr.size());f[0] = arr[0], g[0] = 0;//f[0]=2,g[0]=0for (int i = 1;i < arr.size();i++){f[i] = g[i - 1] + arr[i];g[i] = max(g[i - 1], f[i - 1]);}return max(g[arr.size() - 1], f[arr.size() - 1]);}
};
运行结果:
4.粉刷房子
题目链接
问题:
样例输出和输入:
这道题首先要读懂题,这道题给出二维数组costs[i][j],i表示有多少个房子,然后j表示三种颜色,三种颜色分别是红蓝绿,但是这三种颜色 不能涂在相邻两个格子中,最后让我们求最小的花费
算法原理:
状态表示:dp[i]表示图到第i个房间的最小的花费
状态转移方程:这里由于涉及到三种颜色,这三种颜色分别是三种状态,所以这里我们开辟一个二维数组,这个二维数组的大小是n*3,0表示红色,1表示蓝色,2表示绿色。这里当我们第i个房间,这里我们先对红色进行讨论,由于第n个房间图了红色,所以我们的前一个房间就不能图红色,就只能在蓝色和绿色中选一个颜色,所以这里的最小花费应该是i-1的蓝色和绿色的最小花费中的最小的一个再加上当前位置的红色的最小花费:dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i][0]
其余的也一样:dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i][1],dp[i][2]=dp[i-1][1]+dp[i-1][0])+costs[i][2]
代码展示:
class Solution {
public:int minCost(vector<vector<int>>& costs) {int m = costs.size();int n = costs[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));dp[0][0] = costs[0][0], dp[0][1] = costs[0][1], dp[0][2] = costs[0][2];for (int i = 1;i < m;i++){dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0];dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1];dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2];}return min(min(dp[m - 1][0], dp[m - 1][1]), dp[m - 1][2]);}
};
运行结果:
5.买卖股票的最佳时期含手冷冻期
题目链接
问题:
样例输出和输入:
这道题要我们求是最大的股受益,第一个示例,如果我们买入第一个股票在2的时候卖出则就不能在在3时买入,因为卖出的往后一天处于冷冻期,所以这里我们不能买入股票,冷冻期一过,我们就可以买入股票,我们在0的时候买入一支股票,然后在2的时候卖出,则最大受益就是3.
算法原理:
状态表示:dp[i]表示到达当前位置时的最大利润
状态转移方程:当我们到达i位置时,我们有三种状态,第一种状态是买入(持有股票) ,第二种状态是卖出(未持有股票),第三种状态是冷冻期(冷冻期,不能购买股票)。这三种状态我们分别用0,1,2表示,所以这里我们就可以用一个二维DP表来表示这个dp模型。
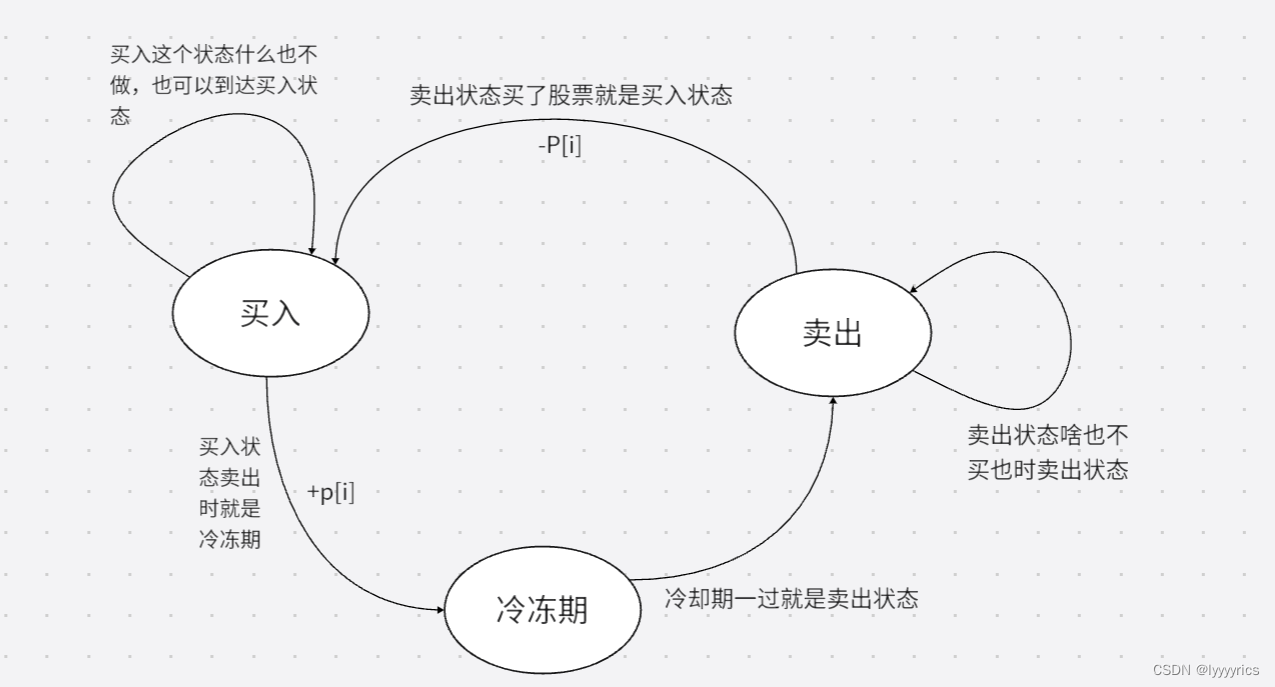
根据上图,我们可以得出简单的状态转移方程,dp[i][0]=max(dp[i-1][1]-prices[i],dp[i-1][0]]),dp[i][0]=max(dp[i-1][2],dp[i--1][1],dp[i][2]=dp[i-1][0]+prices[i]
代码展示:
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(3, 0));//0买入状态,1可交易状态,2冷冻期dp[0][0] = -prices[0], dp[0][1] = 0, dp[0][2] = 0;for (int i = 1;i < n;i++){dp[i][0] = max(dp[i - 1][1] - prices[i], dp[i - 1][0]);dp[i][1] = max(dp[i - 1][2], dp[i - 1][1]);dp[i][2] = dp[i - 1][0] + prices[i];}//如果最后一次交易手里还剩有股票,那么肯定不是最大的利润return max(dp[n - 1][1], dp[n - 1][2]);}
};
运行结果:
总结
在本文中,我们深入探讨了多状态动态规划(DP)问题的核心概念、应用场景和解法技巧。通过分析多状态DP问题的基本结构和挑战,我们不仅回顾了经典的动态规划方法,还揭示了如何在复杂的问题中引入多个状态来实现高效求解。
从具体的算法设计到实际应用案例,我们讨论了如何构建状态转移方程、优化空间复杂度以及处理状态之间的依赖关系。这些高级技巧不仅帮助我们解决了特定的多状态DP问题,也为应对未来更为复杂的算法问题奠定了坚实的基础。
多状态DP不仅是解决动态规划问题的有力工具,更是我们在算法设计中应对多维复杂性的重要思路。通过对这一领域的深入了解,我们可以更好地应对实际问题中的挑战,并在算法竞赛、数据分析等领域中取得突破性进展。
希望本文的讨论能够激发你对多状态动态规划问题的兴趣,鼓励你进一步探索这一领域的高级技巧与创新方法。算法的世界充满了无限可能,而多状态DP问题则是我们探索这片领域的一把重要钥匙。
感谢你的阅读,希望你能从中获得新的启发与收获!
相关文章:

简单多状态DP问题
这里写目录标题 什么是多状态DP解决多状态DP问题应该怎么做?关于多状态DP问题的几道题1.按摩师2.打家劫舍Ⅱ3.删除并获得点数4.粉刷房子5.买卖股票的最佳时期含手冷冻期 总结 什么是多状态DP 多状态动态规划(Multi-State Dynamic Programming, Multi-St…...
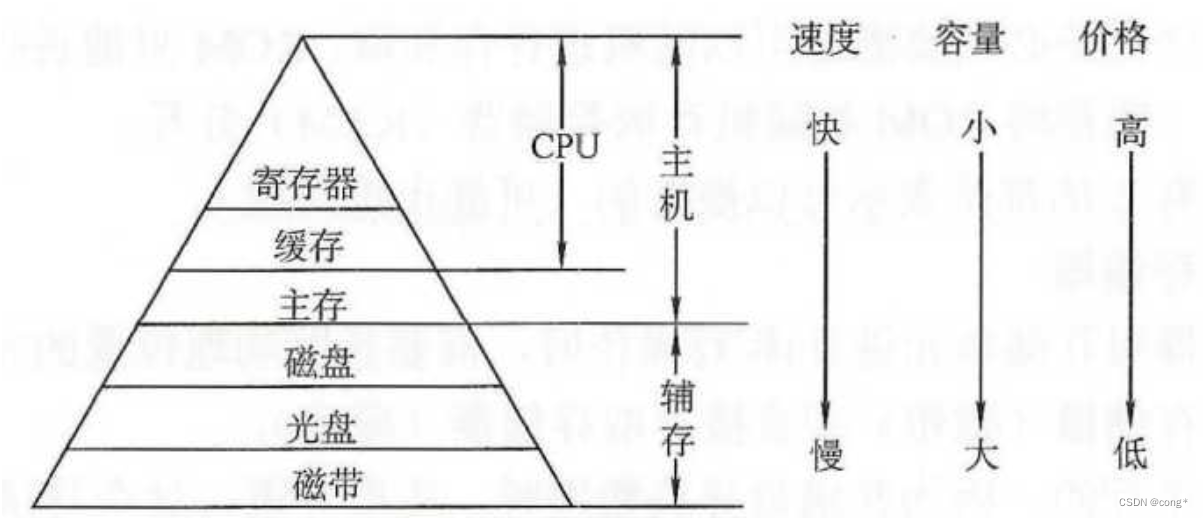
cpu,缓存,辅存,主存之间的关系及特点
关系图 示意图: ------------------- | CPU | | ------------- | | | 寄存器 | | | ------------- | | | L1缓存 | | | ------------- | | | L2缓存 | | | ------------- | | | L3缓存 | | | ------------- | ----…...

【每日刷题】Day77
【每日刷题】Day77 🥕个人主页:开敲🍉 🔥所属专栏:每日刷题🍍 🌼文章目录🌼 1. LCR 159. 库存管理 III - 力扣(LeetCode) 2. LCR 075. 数组的相对排序 - 力…...
macros模块)
chrome-base源码分析(1)macros模块
Chrome-base源码分析(2)之Macros模块 Author:Once Day Date:2024年6月29日 漫漫长路,才刚刚开始… 全系列文章请查看专栏: 源码分析_Once-Day的博客-CSDN博客 参考文档: macros - Chromium Code SearchChrome base 库详解:工…...

玩转springboot之springboot定制嵌入式的servlet
springboot定制嵌入式的servlet容器 修改容器配置 有两种方式可以修改容器的配置 可以直接在配置文件中修改和server有关的配置 server.port8081 server.tomcat.uri-encodingUTF-8//通用的Servlet容器设置 server.xxx //指定Tomcat的设置 server.tomcat.xxx编写一个EmbeddedSer…...
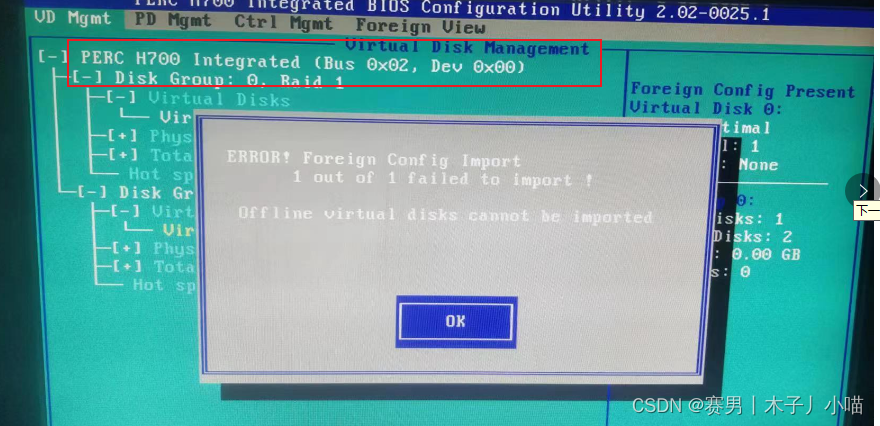
dell服务器RAID5磁盘阵列出现故障的解决过程二——热备盘制作与坏盘替换过程
目录 背景方案概念全局热备(Global Hot Spare):独立热备(Dedicated Hot Spare): 过程8号制作成热备清除配置制作独立热备热备顶替坏盘直接rebuild 更换2号盘2号热备 注意注意事项foreign状态要先清除配置 背…...
Elasticsearch开启认证|为ES设置账号密码|ES账号密码设置|ES单机开启认证|ES集群开启认证
文章目录 前言单节点模式开启认证生成节点证书修改ES配置文件为内置账号添加密码Kibana修改配置验证 ES集群开启认证验证 前言 ES安装完成并运行,默认情况下是允许任何用户访问的,这样并不安全,可以为ES开启认证,设置账号密码。 …...

Excel 数据筛选难题解决
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

Web实时通信的学习之旅:WebSocket入门指南及示例演示
文章目录 WebSocket的特点1、工作原理2、特点3、WebSocket 协议介绍4、安全性 WebSocket的使用一、服务端1、创建实例:创建一个webScoket实例对象1.1、WebSocket.Server(options[,callback])方法中options对象所支持的参数1.2、同样也有一个加密的 wss:/…...

分治精炼宝库-----快速排序运用(⌯꒪꒫꒪)੭
目录 一.基本概念: 一.颜色分类: 二.排序数组: 三.数组中的第k个最大元素: 解法一:快速选择算法 解法二:简单粗暴优先级队列 四.库存管理Ⅲ: 解法一:快速选择 解法二:简单粗…...
快速修复mfc100u.dll丢失解决方案
相连文章:SecureCRT的安装破解 [详细过程2024] 有小伙伴向我反馈在打开SecureFX注册机之后显示【mfc100u.dll找不到】重装之后也没有用,这个是因为Microsoft Visual C的运行时组件和库出现了错误,直接选择重新安装就可以 出现这种情况的原因…...
【C++深度探索】继承机制详解(一)
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页:大耳朵土土垚的博客 …...

力扣第218题“天际线问题”
在本篇文章中,我们将详细解读力扣第218题“天际线问题”。通过学习本篇文章,读者将掌握如何使用扫描线算法和堆来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。 问题描述 力扣第…...
帝国cms未审核文章可视化预览效果
有时候为了让编辑更加清楚的看到别人审核之后的效果,同时文章有需要下一级审核才能在前端展示出来,今天就来展示一个未审核文章预览审核后的效果 这次给某出版社开发的时候,他们需要实现编辑能够预览自己发布之后的审核效果,所以就…...
医院管理系统带万字文档医院预约挂号管理系统基于spingboot和vue的前后端分离java项目java课程设计java毕业设计
文章目录 仓库管理系统一、项目演示二、项目介绍三、万字项目文档四、部分功能截图五、部分代码展示六、底部获取项目源码带万字文档(9.9¥带走) 仓库管理系统 一、项目演示 医院管理系统 二、项目介绍 基于springbootvue的前后端分离医院管…...

爬虫技术在物联网数据采集中的应用
爬虫技术在物联网数据采集中的应用案例主要包括以下几个方面: 电商平台数据采集:例如,使用Python编写的网络爬虫可以用于爬取京东网页相关数据,如品牌、标题、价格、店铺等,并进行数据处理及可视化展示。这种方法不仅可…...
spring boot初始化的几个总结
spring intializr File->New->Project 注意:Spring Initializer中 Java版本选择模块已经不支持1.8了。 Spring Boot 3.x要求 Java最低版本为17, 最新的SpringBoot版本已经要求Java22了 所以,你可以升级Java版本,使用Spri…...

springcloud第4季 seata报could not find any implementation for class
一 问题说明 1.1 描述 在使用seata2.0alibaba-cloud 2022.0.0.0-RC2nacos 2.2.3 模拟下订单分布式事务场景,出现如下问题:java.lang.ArrayIndexOutOfBoundsException: Index 0 out of bounds for length 0 查看服务端:java.util.ServiceCo…...

IT之家最新科技热点
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

对象实例化过程
目录 一、Java对象实例化在JVM中的过程: 类加载与初始化 分配内存 初始化对象内存 设置对象头 执行初始化方法 构造方法执行 二、对象的创建过程 一、Java对象实例化在JVM中的过程: 类加载与初始化: 当JVM需要实例化一个对象时,它…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...