分治精炼宝库-----快速排序运用(⌯꒪꒫꒪)੭
目录
一.基本概念:
一.颜色分类:
二.排序数组:
三.数组中的第k个最大元素:
解法一:快速选择算法
解法二:简单粗暴优先级队列
四.库存管理Ⅲ:
解法一:快速选择
解法二:简单粗暴排序
解法三:简单粗暴优先级队列
一.基本概念:
🐻在计算机科学中,分治法是一种很重要的算法。字面上的解释就是“分而治之”,就是把一个复杂的问题分成两个或则更多个相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小,越容易直接求解,解题所需的计算时间也越少。例如,对于n个元素的排序问题,当n=1时,不需任何计算。n=2时,只要作一次比较即可排好序。n=3时只要作3次比较即可,…。而当n较大时,问题就不那么容易处理了。要想直接解决一个规模较大的问题,有时是相当困难的。🧐分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
当我们对分治算法有了以上的一定了解后,来练习几道题目加深理解~~
注(本文承接上文:分治精炼宝库----归并排序应用( ´◔︎ ‸◔︎`)_用分治法归并排序-CSDN博客)
一.颜色分类:
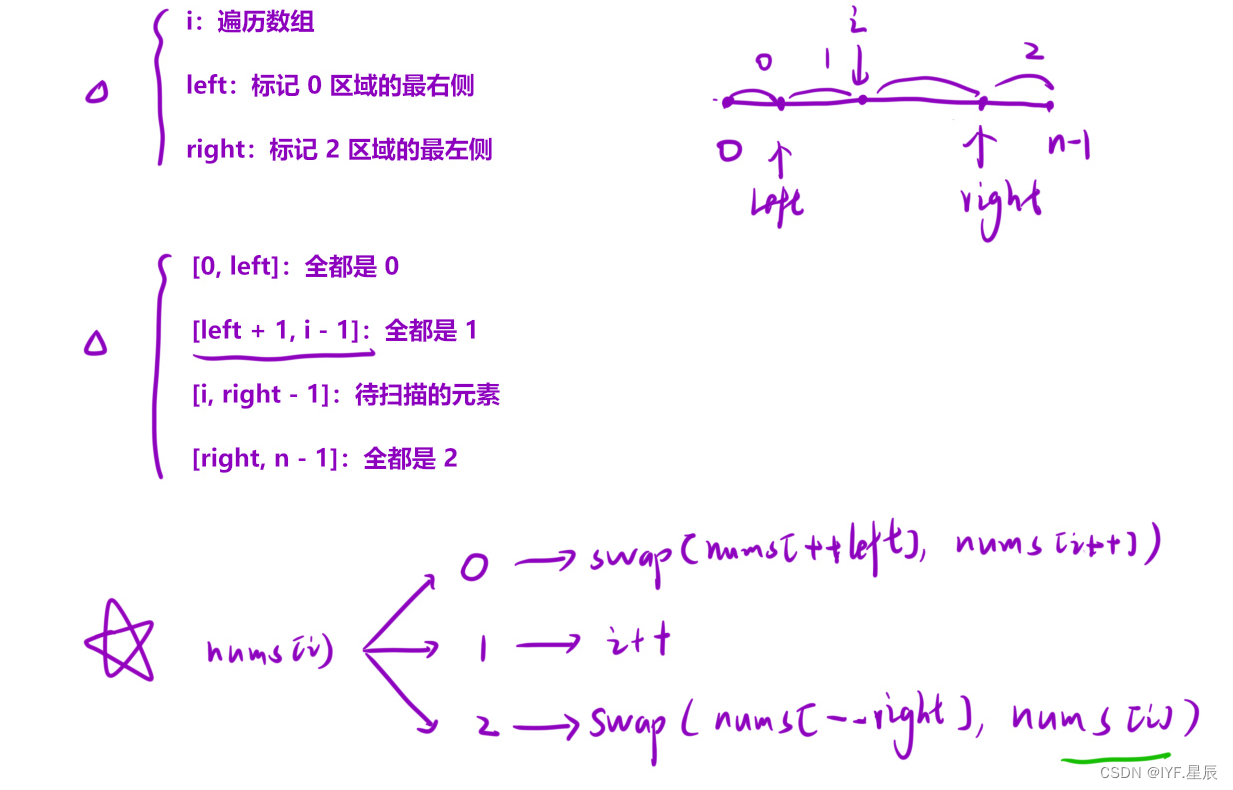
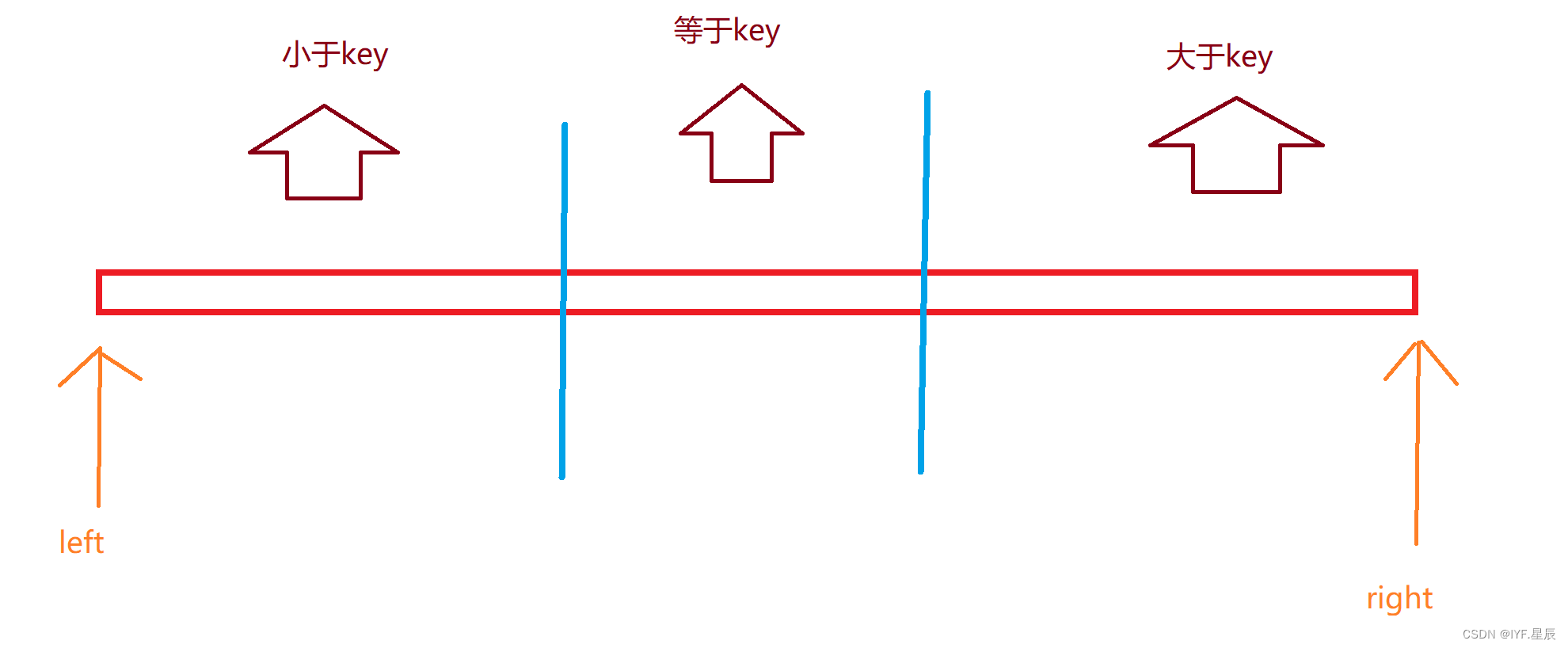
说明:这里我们用到的快速排序会使用数组分三块的思想(下文会详细说明),从数组中随机取一个元素key,将数组划分为三个区域,区域① < key ,区域 ② = key ,区域③ > key
题目链接:75. 颜色分类 - 力扣(LeetCode)

算法思路:
- 使用左指针left和右指针right来划分数组,初始时left为-1,right为数组长度n。
- 遍历数组nums,使用变量i作为当前遍历的索引。
- 如果nums[i]等于0,则将nums[i]与left+1位置的值交换,并将left和i都加1。
- 如果nums[i]等于1,则继续遍历下一个值。
- 如果nums[i]等于2,则将nums[i]与right-1位置的值交换,并将right和i都减1。
- 重复步骤4-6,直到遍历完成整个数组。
核心步骤:
代码详解:
class Solution {public void sortColors(int[] nums) {//将数组划分为三个区域[0,1,2]int n = nums.length;for(int i = 0,left = -1,right = n;i < right;){if(nums[i] == 0){swap(nums,++left,i++);}else if(nums[i] == 1){i++;}else{swap(nums,--right,i);}}}public void swap(int[] nums,int i,int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}运行结果:
二.排序数组:
题目链接:912. 排序数组 - 力扣(LeetCode)

这里我们使用快速排序来解决,首先,我们来一起看一下快速排序的核心框架:
void sort(int[] nums, int lo, int hi) {if (lo >= hi) {return;}// 对 nums[lo..hi] 进行切分// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]int p = partition(nums, lo, hi);// 去左右子数组进行切分sort(nums, lo, p - 1);sort(nums, p + 1, hi);
}快速排序的核心即是先将一个元素排好序,再将剩下的元素排好序
快速排序的核心无疑是 partition 函数, partition 函数的作用是在 nums[lo..hi] 中寻找一个切分点 p,通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p],且 nums[p+1..hi] 都大于 nums[p].
一个元素左边它小,右边都比它大,什么意思?不就是把它放到正确的排好序的位置上了吗?
所以 partition 函数干的事情,其实就是把 nums[p] 这个元素排好序了。
一个元素被排好序了,然后呢?你再把剩下的元素排好序不就行了嘛,排序图解:

其实我们不难发现,拍好序的数组就是一颗二叉搜索树!快速排序的过程其实也就是构造一棵二叉搜索树的过程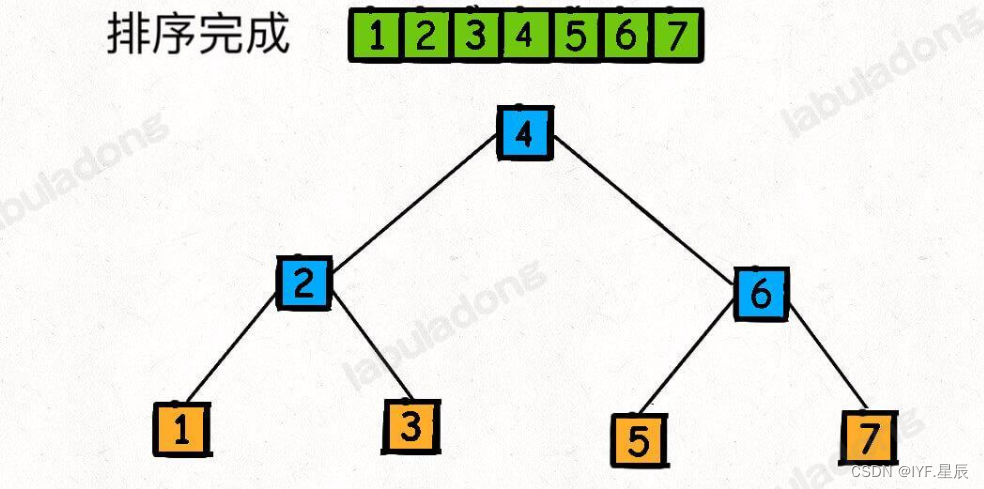
但谈到二叉搜索树的构造,那就不得不说二叉搜索树不平衡的极端情况,极端情况下二叉搜索树会退化成一个链表,导致操作效率大幅降低。这也和快速排序是一样的道理,特别是数组元素都相同的情况下,时间复杂度会大幅上升。
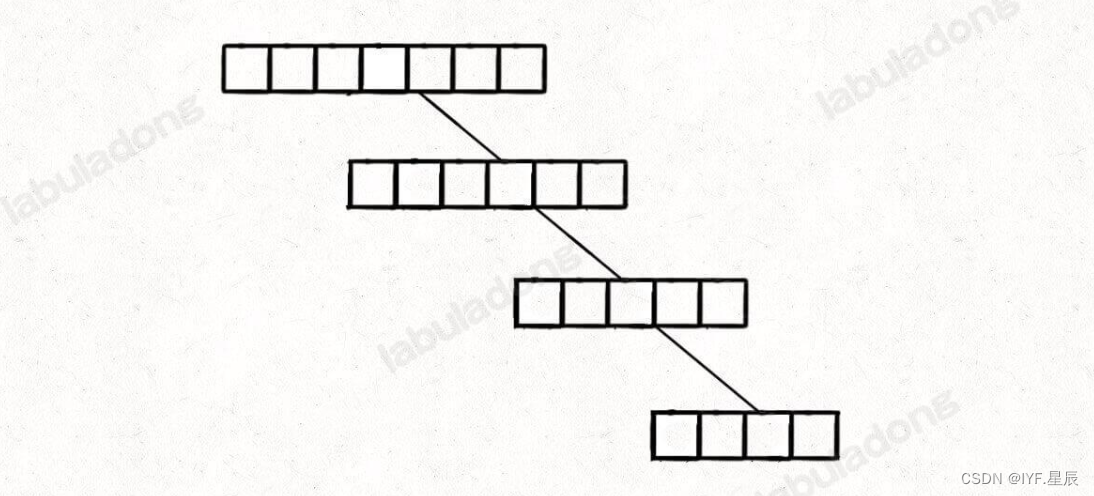
为了避免这种情况,我们要引入随机性:
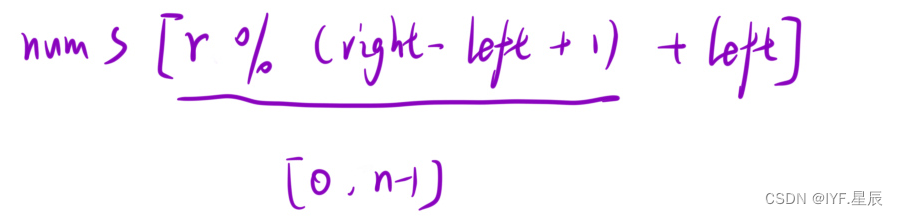
用代码表示就是(取left ~ right 区间的随机数,加上偏移量left):
int key = nums[new Random().nextInt(r - l + 1) + l];快排思路:
从数组中随机取一个元素key,将数组划分为三个区域,区域① < key ,区域 ② = key ,
区域③ > key,然后排序①区间和②区间即可
代码详解:
class Solution {public int[] sortArray(int[] nums) {quickSort(nums,0,nums.length - 1);return nums;}public void quickSort(int[] nums,int l,int r){if(l >= r) return ;//设置一个随机数,然后将数组分为三块int key = nums[new Random().nextInt(r - l + 1) + l];int left = l - 1,cur = l,right = r + 1;while(cur < right){if(nums[cur] < key){swap(nums,++left,cur++);}else if(nums[cur] == key){cur++;}else{swap(nums,--right,cur);}}//在接着往后面找,此时数组区域[l,left] [left + 1,right - 1] [right,r]quickSort(nums,l,left);quickSort(nums,right,r);}public void swap(int[] nums,int i,int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}运行结果:
三.数组中的第k个最大元素:
题目链接:215. 数组中的第K个最大元素 - 力扣(LeetCode)

解法一:快速选择算法
思路:
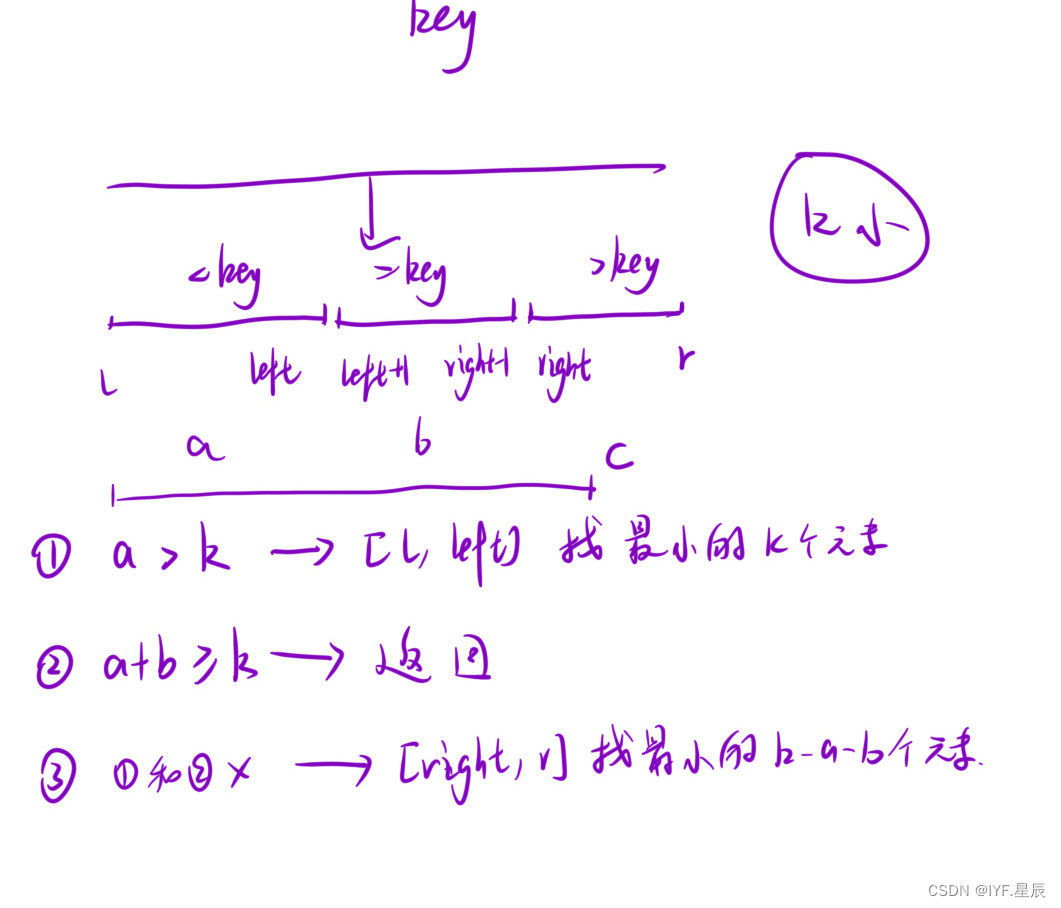
在快排中,当我们把数组「分成三块」之后: [l, left] [left + 1, right - 1] [right, r] ,我们可以通过计算每⼀个区间内元素的「个数」,进⽽推断出我们要找的元素是 在「哪⼀个区间」⾥⾯。那么我们可以直接去「相应的区间」去寻找最终结果就好了:
代码详解:
class Solution {public int findKthLargest(int[] nums, int k) {//快速选择算法,返回第k大的元素int res = quickSort(nums,0,nums.length - 1,k);return res;}public int quickSort(int[] nums,int l,int r,int k){//当只有一个元素或则区间不存在时,直接返回if(l >= r) return nums[l];//数组分三块 [l,left][left + 1,right - 1][right,r]int key = nums[new Random().nextInt(r - l + 1) + l];int left = l - 1,cur = l,right = r + 1;while(cur < right){if(nums[cur] < key){swap(nums,++left,cur++);}else if(nums[cur] == key){cur++;}else{swap(nums,--right,cur);}}//分别对a b c 三个区间做判断,合适的区间int b = right - left - 1,c = r - right + 1;if(c >= k) return quickSort(nums,right,r,k);else if(b + c >= k) return key;//如果都不是,就去[l,left]区间找k - b - c大的元素else return quickSort(nums,l,left,k - b - c);}public void swap(int[] nums,int i,int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}运行结果:
解法二:简单粗暴优先级队列
代码详解:
class Solution {public int findKthLargest(int[] nums, int k) {PriorityQueue<Integer> heap = new PriorityQueue<>((o1,o2)->{return o2.compareTo(o1);});for(int i = 0;i < nums.length;i++){heap.offer(nums[i]);}int res = 0;for(int i = 0;i < k;i++){res = heap.poll();}return res;}
}运行结果:
四.库存管理Ⅲ:
题目链接:LCR 159. 库存管理 III - 力扣(LeetCode)

解法一:快速选择
思路:
在快排中,当我们把数组「分成三块」之后: [l, left] [left + 1, right - 1] [right, r] ,我们可以通过计算每⼀个区间内元素的「个数」,进⽽推断出最⼩的k个数在哪 些区间⾥⾯,那么我们可以直接去「相应的区间」继续划分数组即可:
代码详解:
class Solution {public int[] inventoryManagement(int[] stock, int k) {quickSort(stock,0,stock.length - 1,k);int[] res = new int[k];for(int i = 0;i < k;i++){res[i] = stock[i];}return res;}public void quickSort(int[] nums,int l,int r,int k){if(l >= r) return ;//随机取数int key = nums[new Random().nextInt(r - l + 1) + l];int left = l - 1,cur = l,right = r + 1;while(cur < right){if(nums[cur] < key){swap(nums,++left,cur++);}else if(nums[cur] == key){cur++;}else{swap(nums,--right,cur);}}//寻找区间最小k个值[l,left] [left + 1,right - 1][right,r]int a = left - l + 1,b = right - left - 1;if(a > k) quickSort(nums,l,left,k);else if(a + b >= k) return ;else quickSort(nums,right,r,k - a - b);}public void swap(int[] nums,int i,int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}运行结果:

解法二:简单粗暴排序
代码详解:
class Solution {public int[] inventoryManagement(int[] stock, int cnt) {Arrays.sort(stock);int[] res = new int[cnt];for(int i = 0;i < cnt;i++){res[i] = stock[i];}return res;}
}运行结果:
解法三:简单粗暴优先级队列
代码详解:
class Solution {public int[] inventoryManagement(int[] stock, int cnt) {PriorityQueue<Integer> heap = new PriorityQueue<>();for(int i = 0; i < stock.length; i++){heap.offer(stock[i]);}int[] res = new int[cnt];for(int i = 0;i < cnt;i++){res[i] = heap.poll();}return res;}
}参考资料:
五大常用算法之一:分治算法 - Will_Don - 博客园 (cnblogs.com)
《labuladong算法笔记》
封面来自:《hello 算法》
结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!

相关文章:

分治精炼宝库-----快速排序运用(⌯꒪꒫꒪)੭
目录 一.基本概念: 一.颜色分类: 二.排序数组: 三.数组中的第k个最大元素: 解法一:快速选择算法 解法二:简单粗暴优先级队列 四.库存管理Ⅲ: 解法一:快速选择 解法二:简单粗…...
快速修复mfc100u.dll丢失解决方案
相连文章:SecureCRT的安装破解 [详细过程2024] 有小伙伴向我反馈在打开SecureFX注册机之后显示【mfc100u.dll找不到】重装之后也没有用,这个是因为Microsoft Visual C的运行时组件和库出现了错误,直接选择重新安装就可以 出现这种情况的原因…...
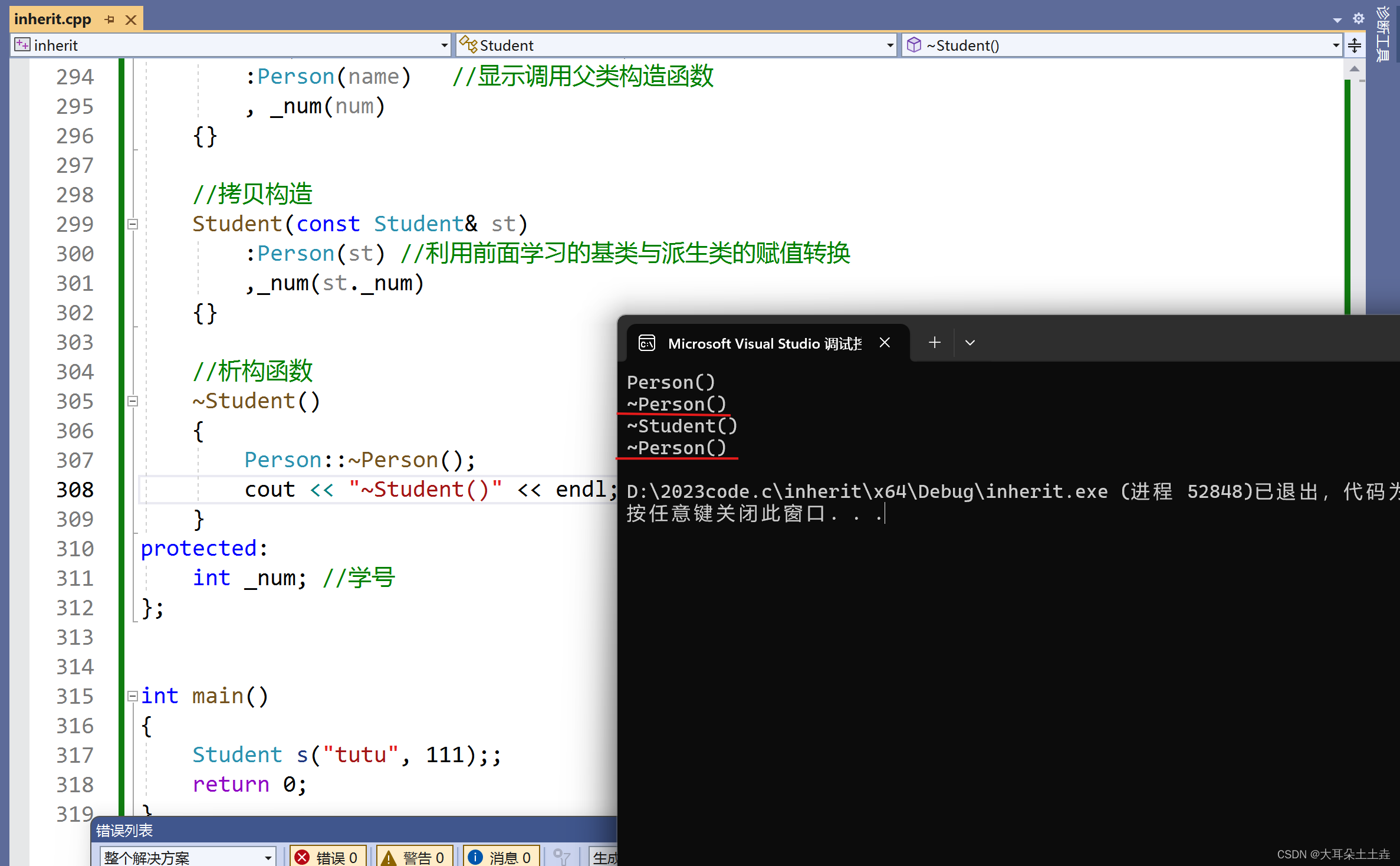
【C++深度探索】继承机制详解(一)
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页:大耳朵土土垚的博客 …...

力扣第218题“天际线问题”
在本篇文章中,我们将详细解读力扣第218题“天际线问题”。通过学习本篇文章,读者将掌握如何使用扫描线算法和堆来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。 问题描述 力扣第…...
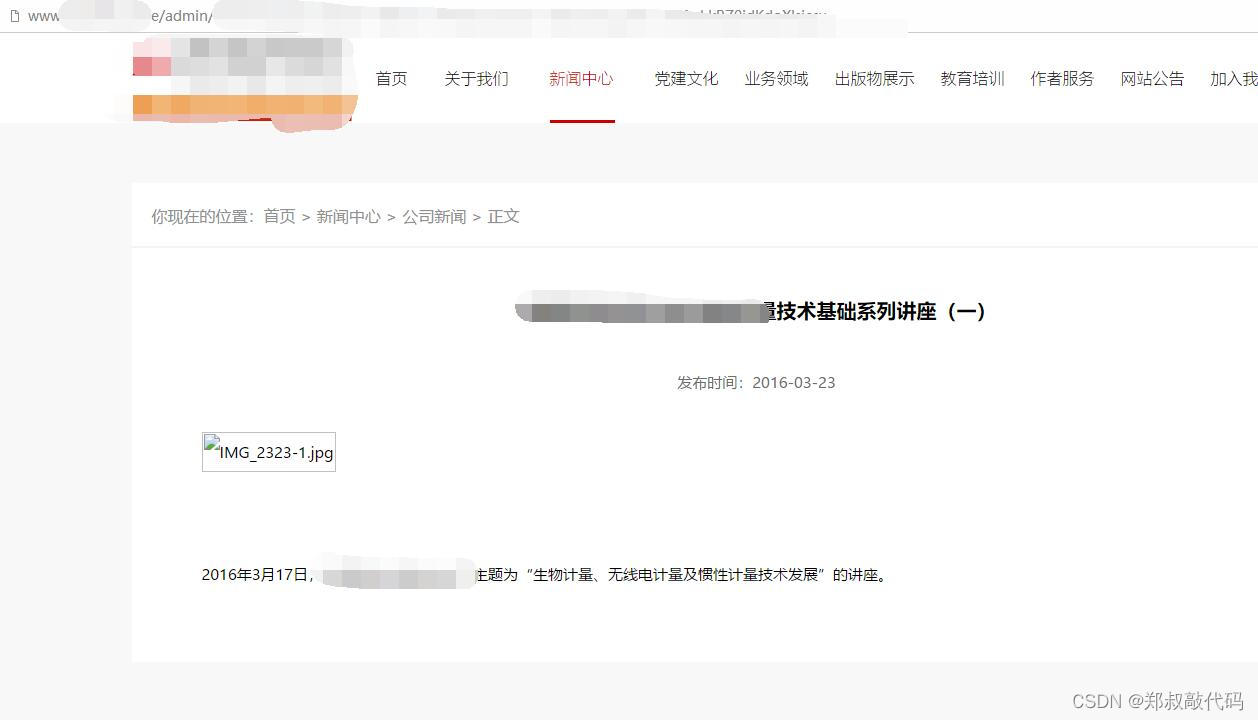
帝国cms未审核文章可视化预览效果
有时候为了让编辑更加清楚的看到别人审核之后的效果,同时文章有需要下一级审核才能在前端展示出来,今天就来展示一个未审核文章预览审核后的效果 这次给某出版社开发的时候,他们需要实现编辑能够预览自己发布之后的审核效果,所以就…...
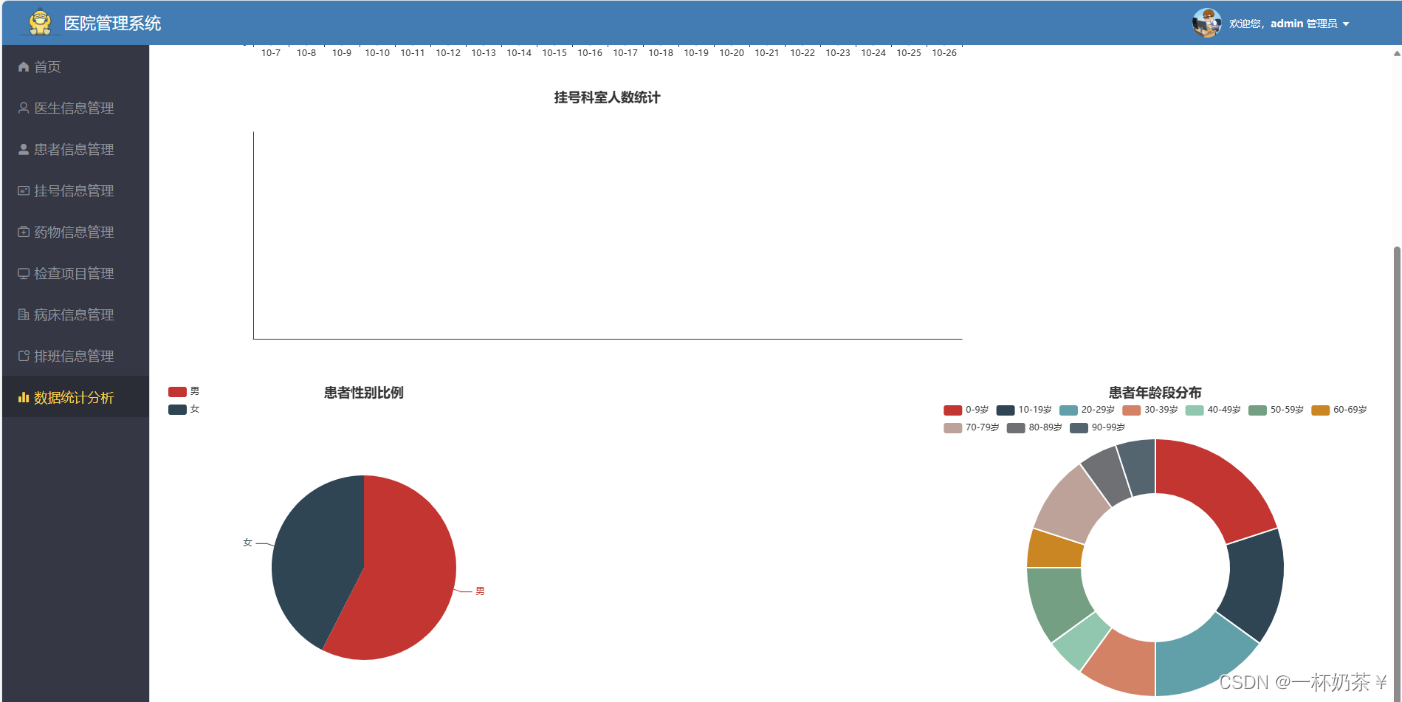
医院管理系统带万字文档医院预约挂号管理系统基于spingboot和vue的前后端分离java项目java课程设计java毕业设计
文章目录 仓库管理系统一、项目演示二、项目介绍三、万字项目文档四、部分功能截图五、部分代码展示六、底部获取项目源码带万字文档(9.9¥带走) 仓库管理系统 一、项目演示 医院管理系统 二、项目介绍 基于springbootvue的前后端分离医院管…...

爬虫技术在物联网数据采集中的应用
爬虫技术在物联网数据采集中的应用案例主要包括以下几个方面: 电商平台数据采集:例如,使用Python编写的网络爬虫可以用于爬取京东网页相关数据,如品牌、标题、价格、店铺等,并进行数据处理及可视化展示。这种方法不仅可…...
spring boot初始化的几个总结
spring intializr File->New->Project 注意:Spring Initializer中 Java版本选择模块已经不支持1.8了。 Spring Boot 3.x要求 Java最低版本为17, 最新的SpringBoot版本已经要求Java22了 所以,你可以升级Java版本,使用Spri…...

springcloud第4季 seata报could not find any implementation for class
一 问题说明 1.1 描述 在使用seata2.0alibaba-cloud 2022.0.0.0-RC2nacos 2.2.3 模拟下订单分布式事务场景,出现如下问题:java.lang.ArrayIndexOutOfBoundsException: Index 0 out of bounds for length 0 查看服务端:java.util.ServiceCo…...

IT之家最新科技热点
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

对象实例化过程
目录 一、Java对象实例化在JVM中的过程: 类加载与初始化 分配内存 初始化对象内存 设置对象头 执行初始化方法 构造方法执行 二、对象的创建过程 一、Java对象实例化在JVM中的过程: 类加载与初始化: 当JVM需要实例化一个对象时,它…...

常见漏洞之XSS
一、XSS简介 XSS(Cross-Site Scripting,跨站脚本攻击)是一种常见的网络攻击方式,通过在网页中注入恶意脚本,当其他用户浏览这些网页时,这些嵌入的恶意脚本会在其浏览器上执行,从而进行各种恶意…...
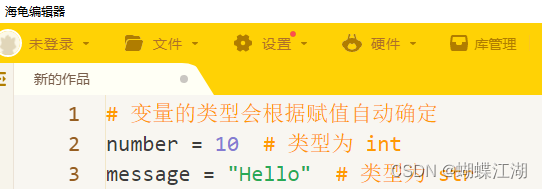
Python变量的命名规则与赋值方式
第二章:Python 基础语法 第一节:变量的命名规则与赋值方式 2.1.1 引言 在编程中,变量是存储数据的基本单元。变量的命名和赋值是编程语言中表达和操作数据的基础。了解和遵循变量命名规则对于编写清晰、可维护的代码至关重要。 2.1.2 变量…...

昇思25天学习打卡营第7天|网络构建
昇思25天学习打卡营第7天|网络构建 前言函数式自动微分函数与计算图微分函数与梯度计算Stop GradientAuxiliary data神经网络梯度计算 个人任务打卡(读者请忽略)个人理解与总结 前言 非常感谢华为昇思大模型平台和CSDN邀请体验昇思大模型!从今…...
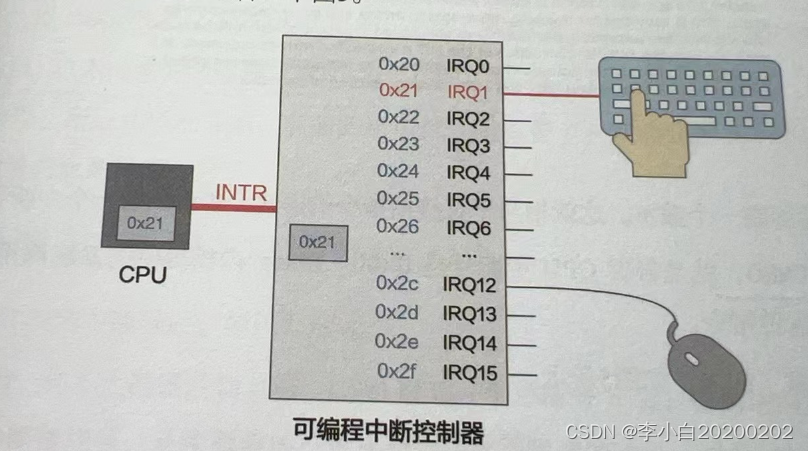
扩展阅读:什么是中断
如果用一句话概括操作系统的原理,那就是:整个操作系统就是一个中断驱动的死循环,用最简单的代码解释如下: while(true){doNothing(); } 其他所有事情都是由操作系统提前注册的中断机制和其对应的中断处理函数完成的。我们点击一下鼠标,敲击一下键盘,执行一个程序,…...

git 命令学习之branch 和 tag 操作
引言 在项目一个迭代过程结束之时,或是一个版本发布之后,我们要进行 新版本的开发,这时就需要对原来的项目代码进行封存,以及新项目代码的开始,这时就需要用到 branch 和 tag 操作。下面简单说说对这两个操作的理解。…...

如何理解 IEEE 754 单精度浮点型能表示的最小绝对值、最大绝对值
文章目录 解答最小绝对值最大绝对值总结 细节理解1. 为什么非规格化数的指数偏移量为126(而不是127)?规格化数与非规格化数非规格化数的指数偏移量非规格化数的尾数非规格化数的值示例 解答 IEEE 754单精度浮点数使用32位来表示一个数值&…...
LeetCode 算法:二叉树的右视图 c++
原题链接🔗:二叉树的右视图 难度:中等⭐️⭐️ 题目 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 示例 1: 输入: [1,2,3,null,5,null,4…...

Java 并发编程常见问题
1、线程状态它们之间是如何扭转的? 1、谈谈对于多线程的理解? 1、对于多核CPU,多线程可以提升CPU的利用率; 2、对于多IO操作的程序,多线程可以提升系统的整体性能及吞吐量; 3、使用多线程在一些场景下可…...

网络基础:静态路由
静态路由是一种由网络管理员手动配置的路由方式,用于在网络设备(如路由器或交换机)之间传递数据包。与动态路由不同,静态路由不会根据网络状态的变化自动调整。 不同厂商的网络设备在静态路由的配置上有些许差异;下面…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...