MATLAB——将直接型转化为并联型和级联型
题目1(IIR):
已知一个系统的传递函数为:
H(z)=8−4z−1+11z−2−2z−31−1.25z−1+0.75z−2−0.125z−3H(z)=\frac{8-4z^{-1}+11z^{-2}-2z^{-3}}{1-1.25z^{-1}+0.75z^{-2}-0.125z^{-3}}H(z)=1−1.25z−1+0.75z−2−0.125z−38−4z−1+11z−2−2z−3
将其由直接型转换为级联型、并联型。信号流图如下图所示。
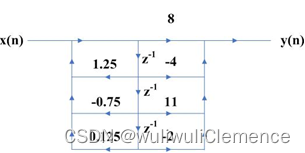
我们先来认识MATLAB自带的两个函数。
residuez
residuez 函数用于计算有理多项式函数在复平面内的极点和残差。其输入参数为分子多项式的系数向量 b 和分母多项式的系数向量 a,输出参数包括极点向量 p、残差向量 r 和常数项 k。
tf2sos
tf2sos 函数则将有理分式函数的分子和分母多项式转换为一组二阶段的、单精度二进制浮点数实现的二阶IIR滤波器系数。tf2sos 的输入参数是分子多项式的系数向量 b 和分母多项式的系数向量 a,输出参数是用于实现滤波器的二阶段滤波器系数 sos 和全局增益 g。
在实际应用中,tf2sos 函数通常用于将高阶滤波器分解为多个二阶IIR滤波器级联的形式,以便更容易实现和分析。而 residuez 函数则常用于计算一些特殊类型的系统的响应,如倒数函数、正切函数等。
代码
b=[8,-4,11,-2];
a=[1,-1.25,0.75,-0.125];
[r,p,c]=residuez(b,a)
[sos,g]=tf2sos(b,a)
部分分式,并联型

H(z)=−8−12i1−(0.5+0.5i)z−1+−8+12i1−(0.5−0.5i)z−1+81−0.25z−1+16H(z)=\frac{-8-12i}{1-(0.5+0.5i)z^{-1}}+\frac{-8+12i}{1-(0.5-0.5i)z^{-1}}+\frac{8}{1-0.25z^{-1}}+16H(z)=1−(0.5+0.5i)z−1−8−12i+1−(0.5−0.5i)z−1−8+12i+1−0.25z−18+16
相乘,级联型

H(z)=8∗1−0.19z−11−0.25z−1∗1−0.31z−1+1.3161z−21−z−1+0.5z−2H(z)=8*\frac{1-0.19z^{-1}}{1-0.25z^{-1}}*\frac{1-0.31z^{-1}+1.3161z^{-2}}{1-z^{-1}+0.5z^{-2}}H(z)=8∗1−0.25z−11−0.19z−1∗1−z−1+0.5z−21−0.31z−1+1.3161z−2
题目2(FIR):
横截型与级联型之间的转换
已知一个FIR系统的传递函数为
H(z)=2+0.9z−1+1.55z−2+2.375z−3H(z)=2+0.9z^{-1}+1.55z^{-2}+2.375z^{-3}H(z)=2+0.9z−1+1.55z−2+2.375z−3
将其从横截型转换为级联型。信号流图如下所示。
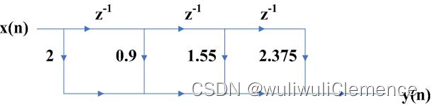
程序
b=[2,0.9,1.55,2.375];
a=[1];
[sos,g]=tf2sos(b,a)
运行结果:

H(z)=2(1+0.95z−1)(1−0.5z−1+1.25z−1)H(z)=2(1+0.95z^{-1})(1-0.5z^{-1}+1.25z^{-1})H(z)=2(1+0.95z−1)(1−0.5z−1+1.25z−1)
相关文章:

MATLAB——将直接型转化为并联型和级联型
题目1(IIR): 已知一个系统的传递函数为: H(z)8−4z−111z−2−2z−31−1.25z−10.75z−2−0.125z−3H(z)\frac{8-4z^{-1}11z^{-2}-2z^{-3}}{1-1.25z^{-1}0.75z^{-2}-0.125z^{-3}}H(z)…...

.NET Framework .NET Core与 .NET 的区别
我们在创建C#程序时,经常会看到目标框架以下的选项,那么究竟有什么区别? 首先 .NET是一种用于构建多种应用的免费开源开发平台,可以使用多种语言,编辑器和库开发Web应用、Web API和微服务、云中的无服务器函数、云原生应用、移动应用、桌面应用、Windows WPF、Windows窗体…...

carla与ros2的自动驾驶算法-planning与control算法开发与仿真
欢迎仪式 carla与ros2的自动驾驶算法-planning与control算法开发与仿真欢迎大家来到自动驾驶Player(L5Player)的自动驾驶算法与仿真空间,在这个空间我们将一起完成这些事情: 控制算法构建基础模块并仿真调试:PID、LQR、Stanley 、MPC、滑膜控…...

corn表达式
简单理解corn表达式:在使用定时调度任务的时候,我们最常用的,就是cron表达式了。通过cron表达式来指定任务在某个时间点或者周期性的执行。cron表达式配置起来简洁方便,无论是Spring的Scheduled还是用Quartz框架,都支持…...
推荐系统中对抗性机器学习-文献综述与未来发展整理分享
对抗学习是一种机器学习技术,旨在通过提供欺骗性输入来欺骗模型。最常见的原因是导致机器学习模型出现故障。大多数机器学习技术旨在处理特定的问题集,其中从相同的统计分布(IID)生成训练和测试数据。当这些模型应用于现实世界时&…...
Proteus8.15安装教程
1、解压Proteus8.15 安装包,然后双击进去,找到setup文件,右键,以管理员身份运行。 2、需要安装一些插件,点击“next”。把插件安装完成。 点击“finfish” 点击“install” 点击“Cancel” 3、如果没有上面步骤&…...
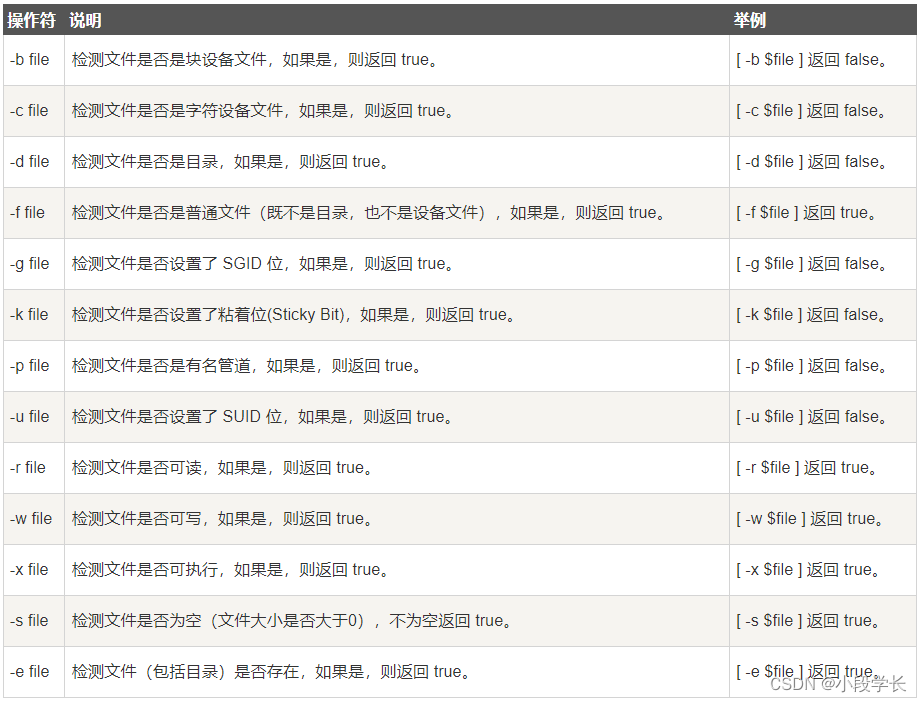
Shell 基本运算符
Shell 和其他编程语言一样,支持多种运算符,包括: 算数运算符关系运算符布尔运算符字符串运算符文件测试运算符 原生bash不支持简单的数学运算,但是可以通过其他命令来实现,例如 awk 和 expr,expr 最常用。…...

Linux基础命令-sed流编辑器
Linux三剑客-grep命令 Sed 一. 命令介绍 先到帮助文档中查看命令的描述信息 NAME sed - stream editor for filtering and transforming text sed命令是操作、过滤和转换文本内容的强大工具,常用功能包括结合正则表达式对文件实现快速增删改查,其中查询…...
)
C语言笔试题(1)
#include <stdio.h> #include <stdlib.h> #include <string.h> void getmemory(char *p) { p(char *) malloc(100); strcpy(p,“hello world”); } int main(void) { char *strNULL; getmemory(str); printf(“%s/n”,str); free(str); return 0; } 上述程序…...
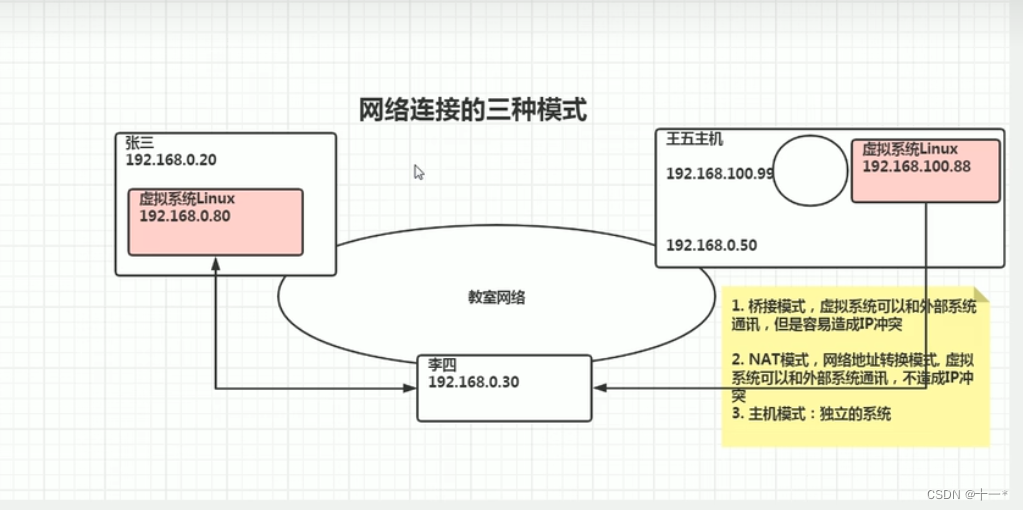
网络连接的三种模式
文章目录前言一、三种连接模式介绍二、三种网络连接模式的区别前言 在进行虚拟机配置时,网络连接分为三种模式:桥接模式,NAT模式,主机模式 一、三种连接模式介绍 张三、李四、王五在同一个网段,所以他们之间可以相互…...

大学模拟电路期末考试模拟题详解
(一)选择题 3.4.5.6.7.8.9.10. (二)填空题 1.漂流电流是温度电流,它由少数、载流子形成、其大小与温度有关,而与外加电压无关。 反向电流是由少数载流子形成、其大小与温度有关,而与外加电压无…...

C/C++内存管理讲解
c/C内存管理讲解 C/C内存分布 首先通过一些题目的引入讲解带大家走进C/C的内存分布。 eg1: 根据上述变量的定义,来判断它们所在的内存位置。 从接下来的4个选项中选出最佳答案填入(注:可重复选)。 A、栈 B、堆 C、数…...
【Linux】网络原理
本篇博客让我们一起来了解一下网络的基本原理 1.网络发展背景 关于网络发展的历史背景这种东西就不多bb了,网上很容易就能找到参考资料,我的专业性欠缺,文章参考意义也不大。这里只做简单说明。 网络发展经过了如下几个模式 独立模式&…...
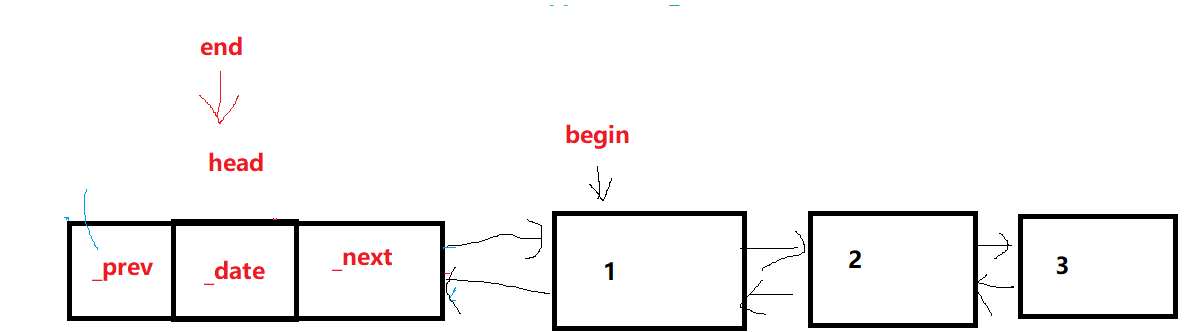
list模拟实现
list模拟实现list原理讲解节点结构list类设计push_backIterators:begin与endconst对象的迭代器重载->运算符反向迭代器迭代器所有代码迭代器总结constructor:clear~listfront与backinsert与erasesize与empty与swappop_back()总代码:节点类正向迭代器类反向迭代器类list类lis…...

CSS看这一篇就够啦,CSS基础大全,可用于快速回顾知识,面试首选
1 CSS简介 CSS 是层叠样式表 ( Cascading Style Sheets ) 的简称。 CSS 是也是一种标记语言,主要用于设置 HTML 页面中的文本内容(字体、大小、对齐方式等)、图片的外形(宽高、边框样式、 边距等)以及版面的布局和外观…...

Canvas详细使用方法(一)
Canvas Canvas的注意事项 < canvas > 和 < img > 元素很相像,唯一的不同就是它并没有 src 和 alt 属性。 -< canvas > 标签只有两个属性——width和height( 单位默认为px )。当没有设置宽度和高度时,canvas 会初始化宽为 300px 和高…...

CentOS定时任务——crontab
crontab Linux crontab 是用来定期执行程序的命令。 crond 命令每分钟会定期检查是否有要执行的工作,如果有要执行的工作便会自动执行该工作。 注意:新创建的 cron 任务,不会马上执行,至少要过 2 分钟后才可以,当然你…...

C51---蓝牙模块---连接软件---控制LED灯
1.器件:C51、HC-08蓝牙模块、Ty-C数据线、杜邦线 2.软件:HC蓝牙助手 3.接线:VCC-VCC、GND-GND、RXD-TXD、TXD-RXD 4.烧写:STC-ISP串口助手 5.代码: #include "reg52.h" #include "intrins.h" …...

Linux 学习笔记——二、主机规划与磁盘分区
一、Linux 与硬件的搭配 Linux 中所有设备均被视为文件,其命名规则如下: 设备文件名SCSI/SATA/USB 硬盘机/dev/sd[a-p]USB 闪存盘/dev/sd[a-p](与 SATA 相同)Virtl/O 界面/dev/vd[a-p](用于虚拟机内)软盘…...
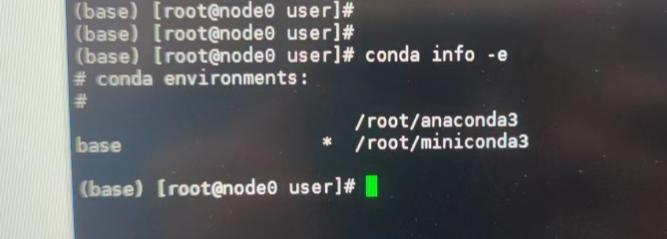
麒麟服务器V10 版本 安装 Anaconda教程,也就是安装Python环境的教程(亲测有效)
目录1 Anaconda 是什么2 安装1 Anaconda 是什么 你可以理解为一个软件,和QQ一样的软件,你安装之后,里面就有naconda包括Conda、Python以及一大堆安装好的工具包,比如:numpy、pandas等 1)包含conda&#x…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
